Similar presentations:
Статистические методы обработки данных
1.
Статистические методы обработкиданных
Литература
1. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Исследование
зависимостей. М. Финансы и статистика, 1985.
2. Фадеева Л.Н., Лебедев А.В. Теория вероятностей и математическая статистика:
Учебное пособие. М., ЭКСМО, 2010.
3. Девис Д. Статистика и анализ геологических данных. М., Мир., 1992.
4. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для
вузов. М., ЮНИТИ-ДАНА, 2007.
5. Лагутин М.Б. Наглядная математическая статистика: Учебное пособие. М.,
БИНОМ. Лаборатория знаний 2007.
6. Чини Р.Ф. Статистические методы в геологии. Решение задач в поле и в
лаборатории. М., Мир, 1986
7. Шестаков Ю.Г. Математические методы в геологии. Красноярск, КГУ, 1988.
2.
ШКАЛЫ ИЗМЕРЕНИЙНоминальная шкала – выражает качественные характеристики. Применимы
лишь логические операции: «равно», «не равно» ;
Порядковая шкала – классификация выполняется по принципу :
«больше-меньше». Интервалы между соседними градациями могут меняться
произвольно;
Интервальная шкала - позволяет не только упорядочивать объекты измерения,
но и численно выразить и сравнить различия между ними.
Шкала отношений – шкала с фиксированным нулем, классифицирующая
объекты пропорционально степени выраженности измеряемого свойства.
Типы величин:
•параметрические (уточняются с возрастанием точности исследования)
•непараметрические
3.
Основные понятия теориии веротностейСобытие – всякий факт, который происходит (или не происходит в
результате проведения опыта или испытания)
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ:
Достоверное событие – событие, которое обязательно произойдет, если будет
осуществлена определенная совокупность условий (проведено испытание);
Невозможное событие – событие, которое заведомо не произойдет, если будет
осуществлена определенная совокупность условий (проведено испытание);
Случайное событие – либо происходит, либо не происходит при проведении
испытания.
Вероятность – численное выражение степени достоверности события
• Вероятность достоверного события равна 1.
• Вероятность невозможного события равна 0.
• Вероятность случайного события есть число, заключенное между 0 и 1.
4.
СЛУЧАЙНЫЕ СОБЫТИЯВИДЫ СЛУЧАЙНЫХ СОБЫТИЙ:
Несовместные события – событие, для которых появление одного из них
исключает появление других в одном и том же испытании;
События образуют полную группу, если в результате испытания обязательно
происходит хотябы одно из них.
Если все события, образующие полную группу, попарно несовместны, то в
результате испытания появится одно и только одно из этих событий.
Равновозможные события – события, для которых степень достоверности
появления при испытании считается одинаковой.
Множество элементарных исходов – множество событий, для которого
выполняются следующие условия:
•события образуют полную группу
•являются попарно несовместными
•являются равновозможными
5.
СЛУЧАЙНЫЕ СОБЫТИЯКлассическое определение вероятности
Пусть для собятия А определено множество элементарных исходов { N }
причём подмножество { m } { N } - благоприятные исходы.
Тогда вероятность события А равна отношению числа благоприятных исходов к
общему числу исходов:
m
P ( A)
N
6.
СЛУЧАЙНЫЕ СОБЫТИЯГеометрическое определение вероятности
Пусть для собятия А определено множество равновозможных исходов, которое
не является конечным.
Тогда вероятность события А можно определить как отношение
геометрической меры благоприятных исходов к геометрической мере всех
возможных исходов:
g
P ( A)
G
7.
СЛУЧАЙНЫЕ СОБЫТИЯДействие над событиями
Суммой нескольких событий называется событие, которое происходит при
наступлении ходя бы одного из данных событий.
C A B
Произведением нескольких событий называется событие, которое происходит
только при совместном наступлении всех данных событий.
C A B
Разностью двух событий называется событие, которое происходит в том случае,
если произойдёт первое событие и не произойдёт второе.
C A\ B
8.
СЛУЧАЙНЫЕ СОБЫТИЯВероятность произведения событий
Вероятность произведения двух событий равна произведению вероятности
одного из них на условную вероятность другогого:
P ( AB ) P ( A) P ( B | A) P ( B ) P ( A | B )
Вероятность произведения множества событий равна произведению
вероятности одного из них на условные вероятности другогих:
N
P ( Ai ) P ( A1 ) P ( A2 | A1 ) P ( A3 | A1 A2 ) ... P ( AN | A1 A2 ... AN 1 )
i 1
9.
СЛУЧАЙНЫЕ СОБЫТИЯВероятность суммы событий
Вероятность суммы двух событий равна сумме вероятностей этих событий за
вычетом вероятности их произведения:
P ( A B ) P ( A) P ( B ) P ( AB )
Для множества событий вероятность их суммы равна:
N
N
P ( Ai ) P ( Ai ) ( 1)
i 1
i 1
N 2 N 1
N
2 1
N 1
N
P( A A )
i 1 j i 1
( 1)3 1 P ( Ai A j Ak ) ...
i 1 j i 1 k j 1
i
j
10.
СЛУЧАЙНЫЕ СОБЫТИЯВероятности суммы и произведения событий
Вероятность произведения двух или нескольких независимых (независимых в
совокупности) событий равна произведению вероятностей этих событий:
N
N
i
i 1
P ( Ai ) P ( Ai )
Вероятность суммы двух (множества) несовместных (попарно несовместных)
событий равна сумме вероятностей этих событий:
N
N
i 1
i 1
P ( Ai ) P ( Ai )
Сумма вероятностей событий, образующих полную группу, равна 1.
Вероятность суммы нескольких совместных событий, равна разности между
единицей и вероятностью произведения противоположных им событий:
N
N
i 1
i 1
P ( Ai ) 1 P ( Ai )
11.
СЛУЧАЙНЫЕ СОБЫТИЯФормула полной вероятности
Пусть событие A может произойти только при совместном наступлении с одним
из событий B1, B2, … BN, образующих полную группу (множество {BN} называется
множеством гипотез). Тогда вероятность события А будет равна:
N
P ( A) P ( Bi ) P ( A | Bi )
i 1
Вероятности гипотез (формула Байеса)
Пусть событие A произошло при совместном наступлении с одним из событий
B1, B2, … BN, (множество гипотез). Тогда вероятность того, что А наступило
совместно с событием Bk { B }N равна:
P ( Bk | A) N
P ( Bk ) P ( A | Bk )
P(B ) P( A | B )
i 1
i
i
12.
СЛУЧАЙНЫЕ СОБЫТИЯПовторные независимые испытания.
Формула Бернулли
Пусть проводятся повторные независимые испытания, в каждом из которых
вероятность наступления события A одинакова и равна p. Тогда вероятность
того, что проведении n испытаний событие А произойдёт k раз, равна:
P ( An ,k ) C p q
k
n
где q = 1-p
k
n k
13.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫСлучайная величина (с.в.) – переменная, которая в результате
испытаний принимает одно из возможного множества своих значений,
причём заранее не известно – какое именно
Случайная величина – функция, заданная на множестве элементарных
исходов (в пространстве элементарных событий).
X = f(w)
Дискретная случайная величина определена на счётном множестве
значений.
Непрерывная случайная величина – принимает всё множество
значений на заданном интервале (конечном или бесконечном) числовой оси.
14.
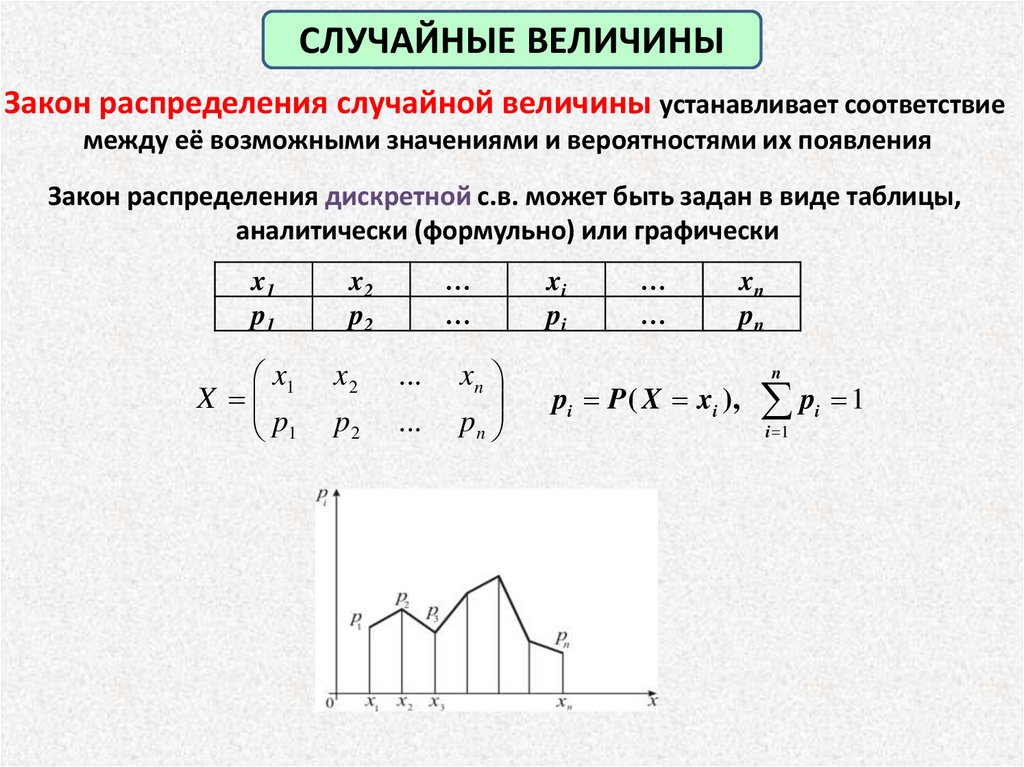
СЛУЧАЙНЫЕ ВЕЛИЧИНЫЗакон распределения случайной величины устанавливает соответствие
между её возможными значениями и вероятностями их появления
Закон распределения дискретной с.в. может быть задан в виде таблицы,
аналитически (формульно) или графически
…
…
x1
p1
x2
p2
x1
X
p1
x2
...
p2
...
xn
pn
xi
pi
…
…
xn
pn
n
pi P ( X xi ), pi 1
i 1
15.
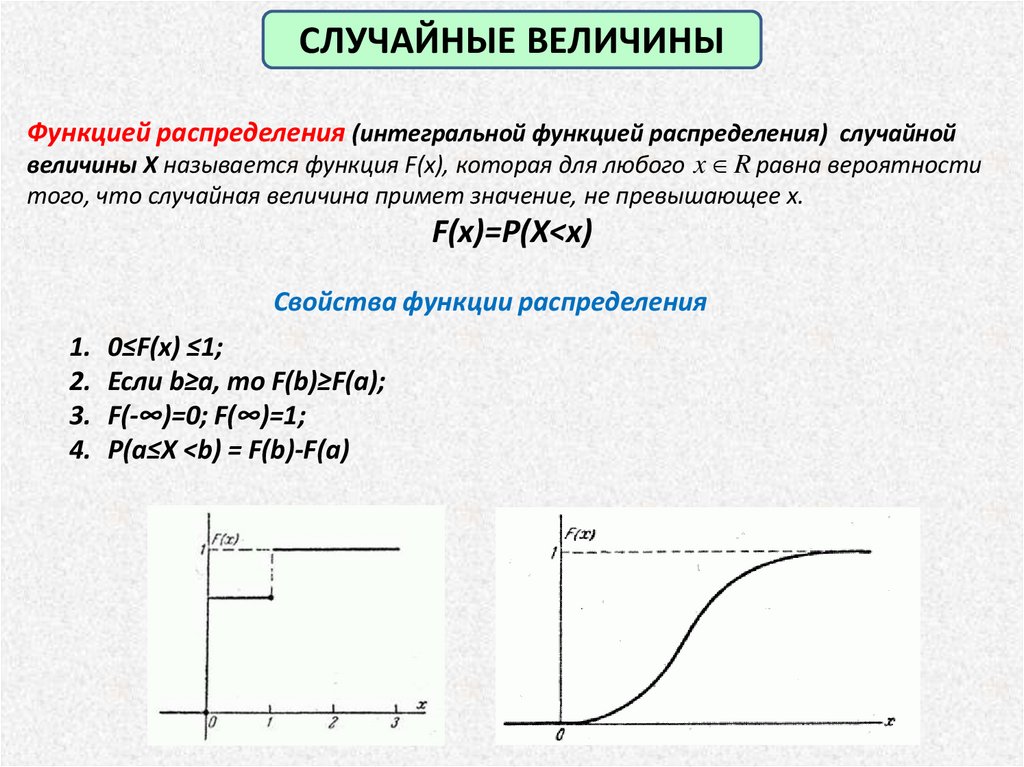
СЛУЧАЙНЫЕ ВЕЛИЧИНЫФункцией распределения (интегральной функцией распределения) случайной
величины X называется функция F(x), которая для любого x R равна вероятности
того, что случайная величина примет значение, не превышающее x.
F(x)=P(X<x)
Свойства функции распределения
1. 0≤F(x) ≤1;
2. Если b≥a, то F(b)≥F(a);
3. F(-∞)=0; F(∞)=1;
4. P(a≤X <b) = F(b)-F(a)
16.
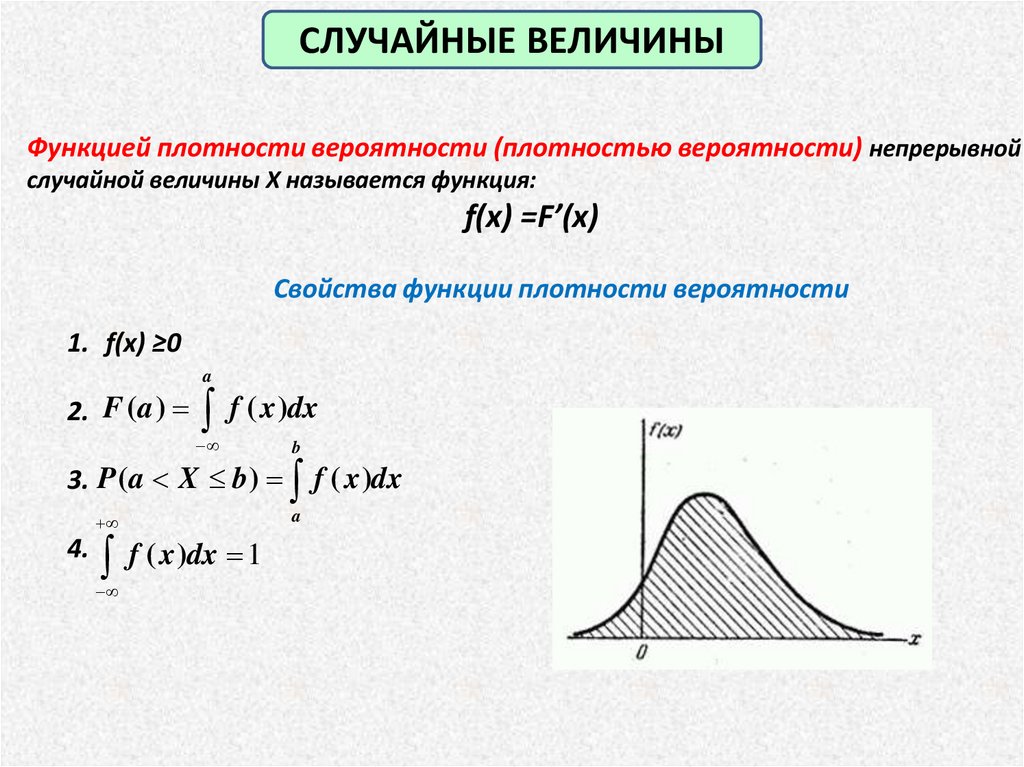
СЛУЧАЙНЫЕ ВЕЛИЧИНЫФункцией плотности вероятности (плотностью вероятности) непрерывной
случайной величины X называется функция:
f(x) =F’(x)
Свойства функции плотности вероятности
1. f(x) ≥0
a
2. F (a )
f ( x )dx
3. P (a X b )
4.
f ( x )dx 1
b
f ( x )dx
a
17.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫЧисловые характеристики случайных величин
Математическим ожиданием дискретной случайной величины
называется сумма произведение всех её возможных значений на
вероятности их появления
n
M ( X ) xi pi
i 1
Для непрерывной случайной величины:
M ( X ) x f ( x )dx
18.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫСвойства математического ожидания
1.
2.
3.
4.
5.
M(C) = C (C – константа);
M(C∙X) = C∙M(X);
M(X±Y)=M(X) ± M(Y);
Для независимых X и Y: M(X∙Y)=M(X)∙M(Y);
M(X) = S2 – S1.
19.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫЧисловые характеристики случайных величин
Дисперсией случайной величины X называется математическое ожидание
квадрата отклонения с.в. от её математического ожидания
D( X ) M (( X M ( X ))2 )
Для дискретной случайной величины:
n
D( X ) ( xi M ( X )) pi
2
i 1
Для непрерывной случайной величины:
D( X ) ( x M ( X ))2 f ( x )dx
20.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫСвойства дисперсии
1.
2.
3.
4.
D(C) = 0 (C – константа);
D(C∙X) = C2∙D(X);
Для независимых X и Y: D(X±Y)=D(X)+D(Y);
D(X) = M((X-M(X))2) = M(X2)-(M(X))2.
Среднеквадратичное стандартное отклонение
( X ) D( X )
21.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫЧисловые характеристики случайных величин
Модой Mo(X) случайной величины X называется её наиболее вероятное
значение
Медианой Me(X) случайной величины X называется такое её значение,
для которого: P(X < Me(X)) = P(X > Me(X)) = 1/2
Квантилем уровня q (q-квантилем) называется такое
значение xq случайной величины, при котором функция её распределения
принимает значение равное q.
F(xq) = q
Моменты распределения случайной величины
Начальный момент k-го порядка: mk=M(Xk)
Центральный момент k-го порядка: mk=M((X-M(X))k)
22.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫЧисловые характеристики случайных величин
Коэффициент асимметрии (асимметрия) A распределения случайной
величины характеризует симметричность графика функции плотности
вероятности.
A = m3/ 3 = m3/(m2)3/2.
Коэффициент эксцесса (эксцесс) E распределения случайной величины
характеризует вид (островершинность/плосковершинность) графика
функции плотности вероятность в области её максимума
E = m4/ 4 - 3 = m3/(m2)2 - 3 .
23.
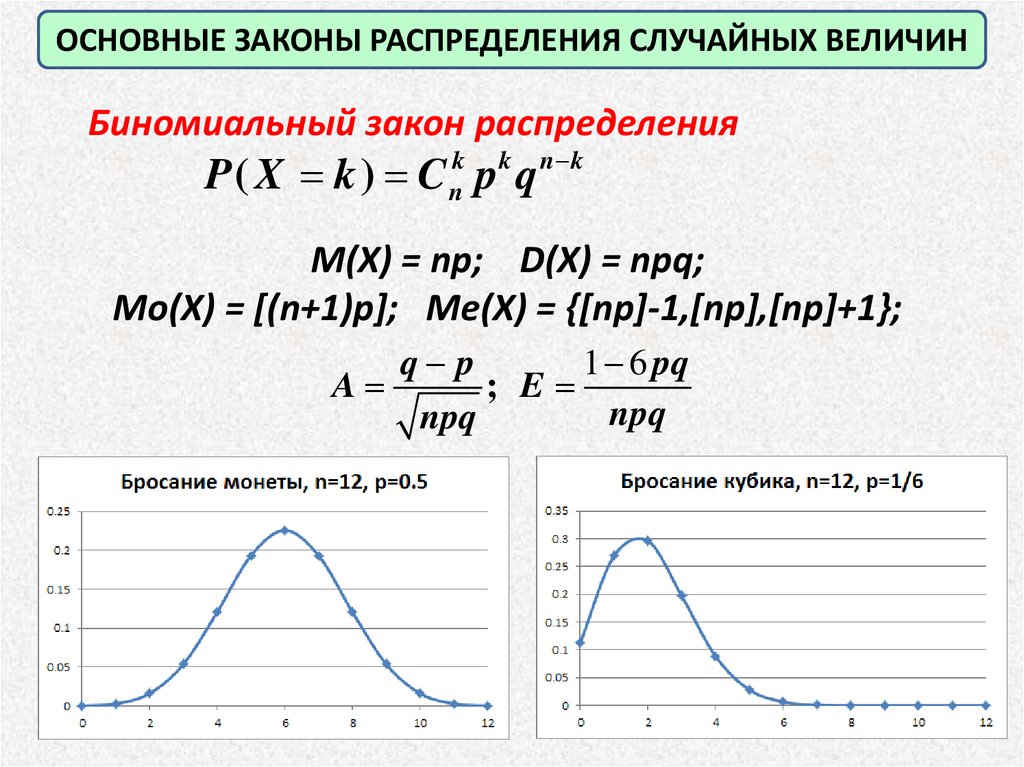
ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИНДискретные случайные величины
Биномиальный закон распределения
P( X k ) C p q
k
n
k
n k
M(X) = np; D(X) = npq
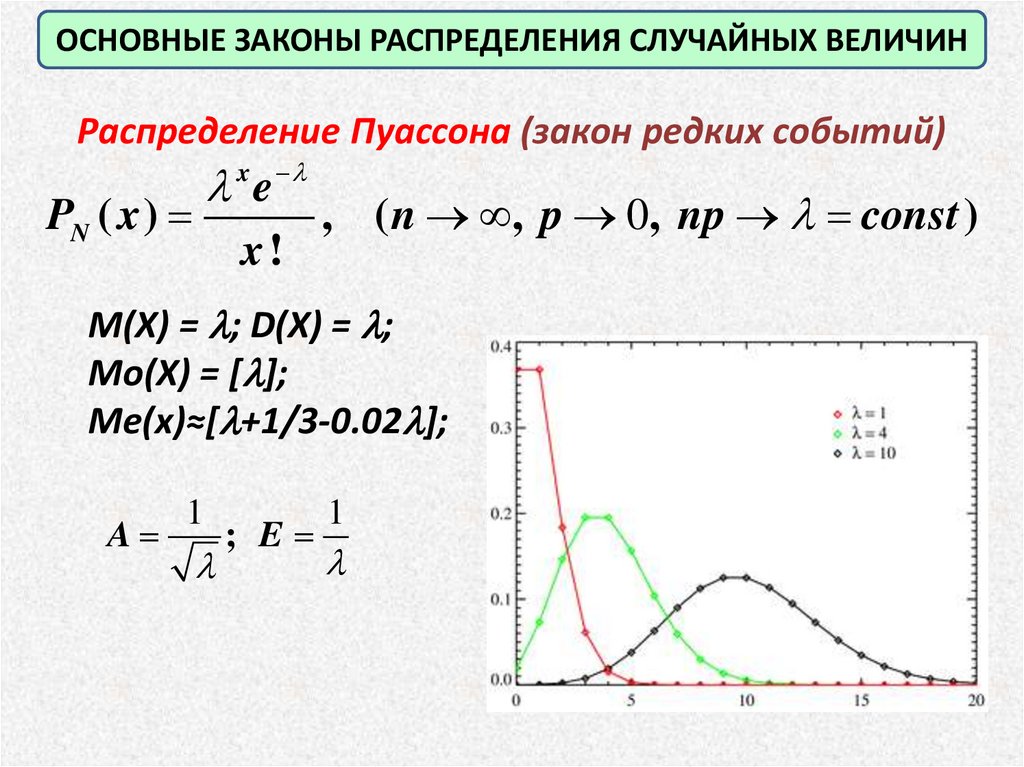
Распределение Пуассона
P( X k )
k e
k!
, ( n , p 0, np const )
M(X) = ; D(X) =
24.
ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИНБиномиальный закон распределения
P( X k ) C p q
k
n
k
n k
M(X) = np; D(X) = npq;
Мо(X) = [(n+1)p]; Me(X) = {[np]-1,[np],[np]+1};
q p
1 6 pq
A
; E
npq
npq
25.
ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИНРаспределение Пуассона (закон редких событий)
x
e
PN ( x )
x!
, ( n , p 0, np const )
M(X) = ; D(X) = ;
Mo(X) = [ ];
Me(x)≈[ +1/3-0.02 ];
A
1
; E
1
26.
ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИНРавномерное распределение
1
, a x b
f ( x) b a
0, x a x b
0,
x a
( x a)
F ( x)
, a x b
(b a )
1,
x b
M ( X ) Me( X )
( b a )2
D( X )
,
12
6
A 0, E
5
a b
,
2
27.
ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИНПоказательное (экспоненциальное) распределение
e x , x 0
f ( x)
0, x 0
x 0
0,
F ( x)
x
1 e , x 0
M(X )
1
, D( X )
1
2
Mo( X ) 0, Me( X )
A 2,
E 6
,
ln 2
,
28.
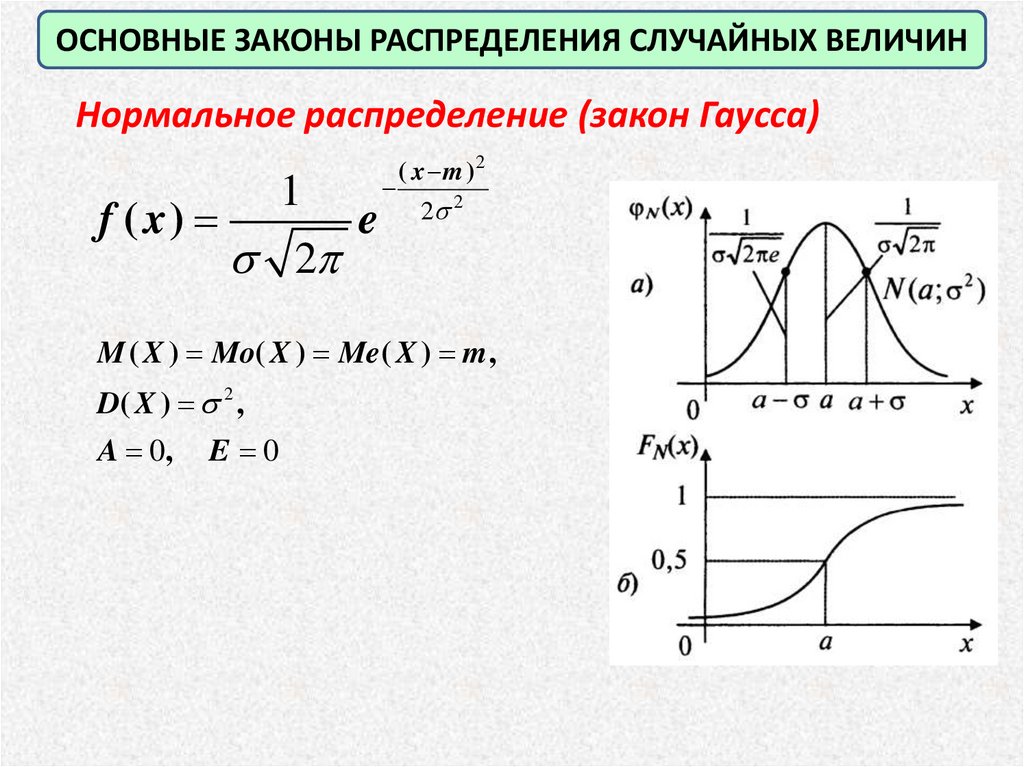
ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИННормальное распределение (закон Гаусса)
f ( x)
1
2
e
( x m )2
2 2
M ( X ) Mo( X ) Me( X ) m ,
D( X ) 2 ,
A 0, E 0
29.
ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИННормальное распределение (закон Гаусса)
b
P ( x [a; b])
a
1
2
e
( x m )
2
2
b m
2
dx ( t
x m
) e
t2
2
dt
a m
b m
P ( x [a; b]) e
a m
t2
2
dt e
t2
2
dt (
P ( x [m 3 ; m 3 ]) 0.9973,
P ( x [m 2 ; m 2 ]) 0.9545,
P ( x [m ; m 1 ]) 0.6827
b m
) (
a m
)
30.
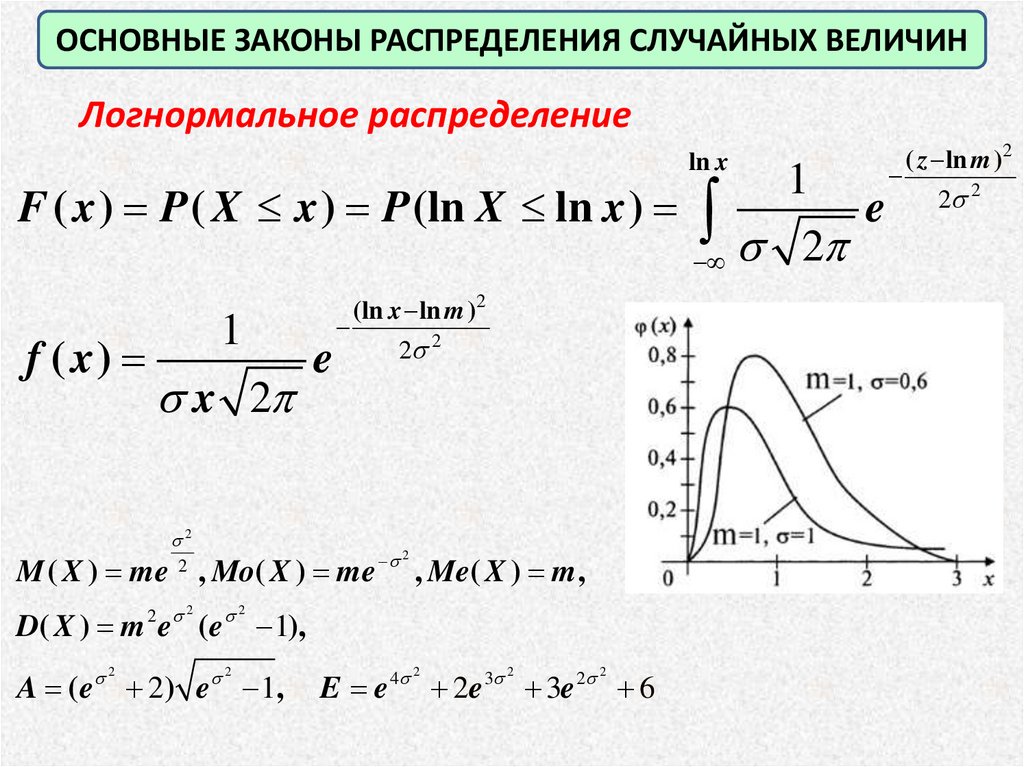
ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИНЛогнормальное распределение
ln x
F ( x ) P ( X x ) P (ln X ln x )
f ( x)
1
x 2
2
(ln x ln m )2
e
M ( X ) me , Mo( X ) me
2
2 2
D( X ) m e ( e
A (e
2
2) e
2
2
2 2
2
, Me( X ) m ,
1),
1,
E e
4 2
2e
3 2
3e
2 2
6
1
2
e
( z ln m )2
2 2
31.
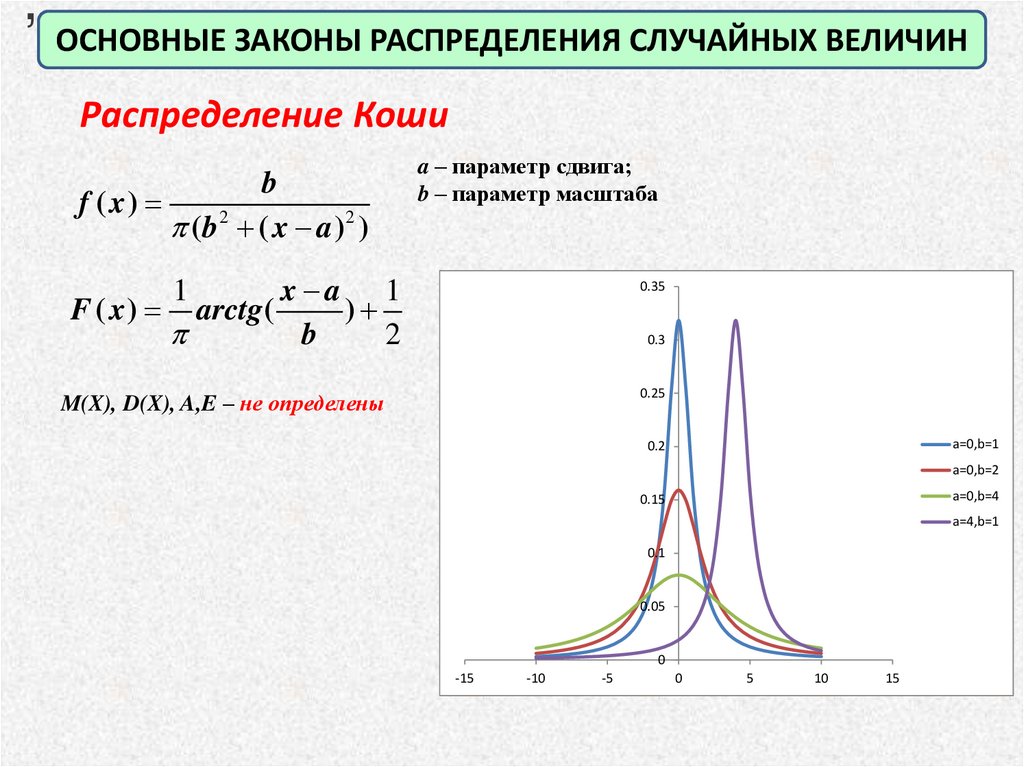
,ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
Распределение Коши
f ( x)
b
( b 2 ( x a )2 )
a – параметр сдвига;
b – параметр масштаба
x a 1
F ( x ) arctg (
)
b
2
1
0.35
0.3
0.25
M(X), D(X), A,E – не определены
a=0,b=1
0.2
a=0,b=2
a=0,b=4
0.15
a=4,b=1
0.1
0.05
0
-15
-10
-5
0
5
10
15
32.
Методы математической статистикиГенеральная совокупность – всё множество объектов
(наблюдений), подлежащая изучению.
Выборочная совокупность (выборка) – конечная (как
правило, небольшая) часть генеральной совокупности,
отобранная для непосредственного изучения.
Сущность выборочного метода – оценить свойства всей
генеральной совокупности по некоторой её части (выборке).
33.
Методы математической статистикиВыборка является репрезентативной, если она достоверно и
полно отражает признаки генеральной совокупности, частью
которой является.
Виды выборок:
• собственно-случайная – отбор происходит случайным образом, без
расчлененияч на группы;
• механическая – отбор производится через определенный интервал;
• типическая (стратифицированная) – отбор производится
случайным образом из отдельных групп, на которые разбивается
генеральная совокупность;
• серийная – выборка разбивается на некоторые группы (серии),
которые подвергаются сплошному (полному) опробованию.
Способы отбора:
• повторный (с возвращением элементов в генеральную совокупность)
• безповторный (без возвращения выбранных элементов)
34.
Методы математической статистикиОценки параметров
Оценкой * параметра называют всякую функцию результатов
наблюдений (или статистику) над случайной величиной Х, с помощью
которой судят о значении параметра
* = f(X1, X2, …., Xn)
т.к. значения X1, X2, …., Xn – случайные величины, то и оценка *, в
отличие от теоретического (генерального) параметра , - случайная
величина
35.
Методы математической статистикиСвойства оценок
Оценка * параметра называется несмещённой, если её
математическое ожидание равно оцениваемому параметру:
M( *)= .
Оценка * параметра называется состоятельной, если она сходится по
вероятности к оцениваемому параметру (при увеличении числа
наблюдений возрастает точность оценивания) :
P
lim P (| * | ) 1, или *
n
n
Несмещённая оценка параметра называется эффективной, если она имеет
наименьшую дисперсию среди всех несмещённых оценок параметра ,
вычесленных по выборкам одного и того же объёма.
36.
Методы математической статистикиОценивание параметров генеральной совокупности по выборке
1. Выборочное среднее (оценка математического ожидания)
n
X
X
i 1
i
n
2. Выборочные дисперсии и среднеквадратичное стандартное отклонение
при известном мат. ожидании:
n
2
(
X
m
)
i
S i 1
n
;
n
при неизвестном известном мат. ожидании:
(X X )
S i 1
n 1
n
s
S
( X i m )2
i 1
n
2
i
;
n
s
S
(X X )
i 1
i
n 1
2
37.
Методы математической статистикиОценивание параметров генеральной совокупности по выборке
Логнормальное распределение
Выборочное среднее геометрическое
n
X ant log(
log( X )
i
i 1
n
n
) n Xi
i 1
2. Выборочное среднеквадратичное стандартное отклонение
(стандартный множитель
n
ant log( slg ) ant log(
2
(log(
X
)
log(
X
))
i
i 1
n 1
)
38.
Методы математической статистикиОценивание параметров генеральной совокупности по выборке
1. Выборочная медиана
MED X ( n 1)/ 2 , для нечётных n
MED
X n / 2 1 X n / 2 1
, для чётных n
2
2. Выборочные асимметрия и эксцесс
n
(X X )
n
A
(X X )
3
i 1
n s3
для конечных n
E i 1
,
4
n s
для конечных n
4
3,
n
n
A
(X X )
n
i 1
( n 1) ( n 2)
s
3
3
(X X )
n( n 1)
E
i 1
( n 1) ( n 2) ( n 3)
s4
4
3( n 1)2
( n 2)( n 3)
39.
Методы математической статистикиИнтервальное оценивание
Доверительный интервал - числовой интервал (X1*, X2*), который с
заданной вероятностью g накрывает неизвестное значение параметра X
Доверительные интервалы среднего
Для выборки с известной дисперсией
P (| X M ( X ) | 1
( x)
) 1 ,
n
( x)
( x)
т .е . X1* X 1
, X 2* X 1
2
2
n
n
где -квантиль нормального закона распределения
2
F ( )
x1- /2
0.05
1.96
0.01
2.58
0.001
3.29
40.
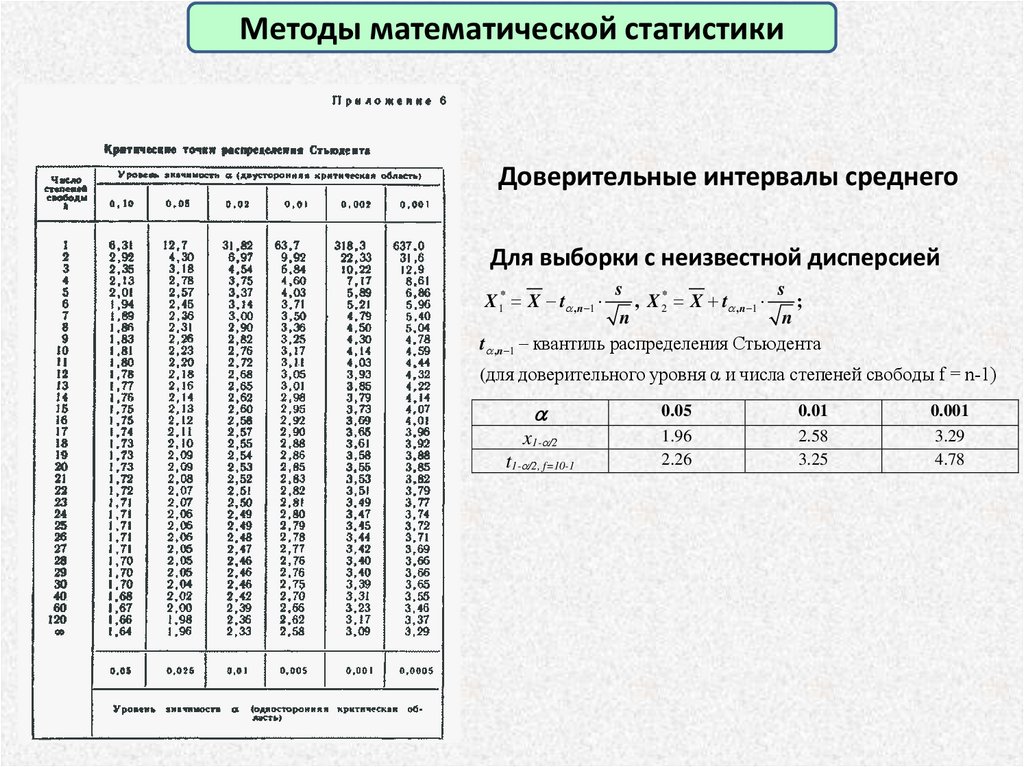
Методы математической статистикиДоверительные интервалы среднего
Для выборки с неизвестной дисперсией
X1* X t ,n 1
s
, X 2* X t ,n 1
s
;
n
n
t ,n 1 квантиль распределения Стьюдента
(для доверительного уровня α и числа степеней свободы f = n-1)
x1- /2
t1- /2, f=10-1
0.05
1.96
2.26
0.01
2.58
3.25
0.001
3.29
4.78
41.
Методы математической статистикиДоверительный интервал дисперсии
P(
nS 2
(21 g )
2
D( X )
, n 1
nS 2
(21 g )
2
) g
, n 1
где g2,n 1 - табличные значения распределения Пирсона
X 1.2, 1.22, 1.2, 1.3, 1.1, 1.15, 1.18, 1.25
X 1.2, S 2 0.00368, s 0.0607
g 0.95 ( 0.05)
t0.05,7 2.36
02.975,7 1.69, 02.025,7 16
t
s
m X a ,n 1 1.2 0.05
n
1
2
s n
2
(1 g ) , n 1
2
s n
2
(1 g ) , n 1
2
0.0429
0.132
42.
Проверка соответствия выборочного распределениянормальному закону
Нормальный закон распределения
f ( x)
1
2
e
( x m )2
2 2
M ( x ) Me( x ) Mo( x ) m; D( x ) 2 ; A 0, E 0
Центральная предельная теорема (теорема Ляпунова):
Если X1,X2 …, Xn – независимые случайные величины, каждая из которых существует
математическое ожидание M(Xi) = ai, дисперсия D(X)= i2 и абсолютный центральный
момент третьего поряка M(|Xi-ai|)=mi, причём
lim
n
m
( ( ))
i
2
i
3/ 2
0
то закон распределения случ. величины Y = X1+X2+ … + Xn при n ∞ неограниченно
приближается к нормальному с M(Y) = S(ai) и D(Y) = S( i2)
43.
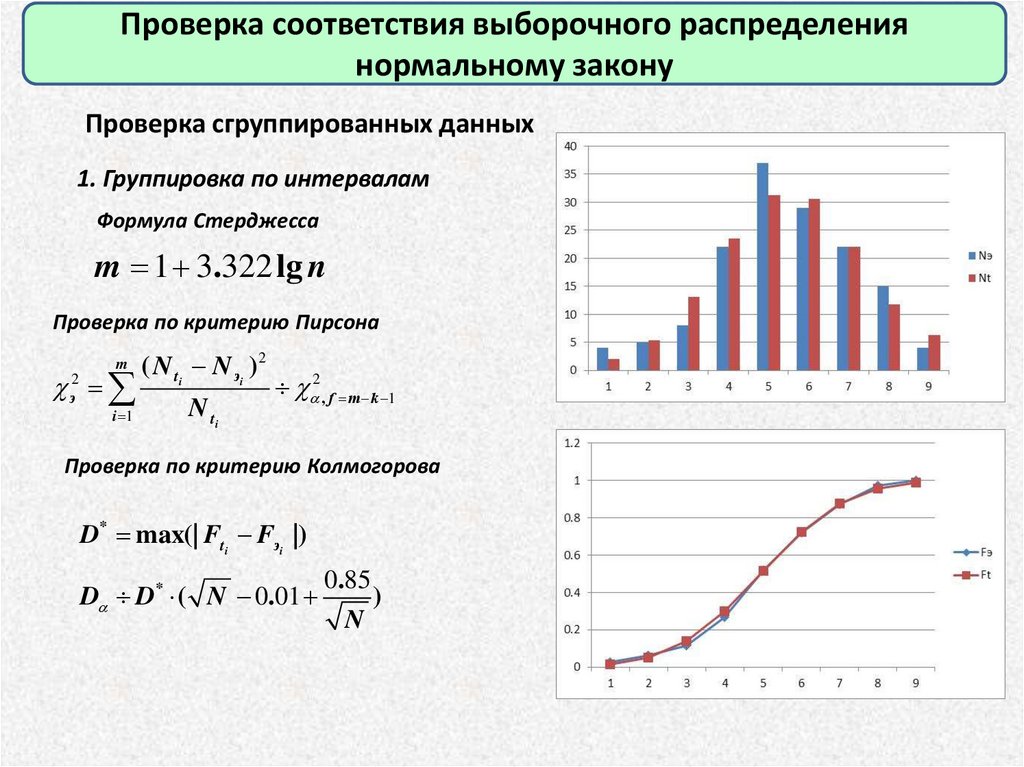
Проверка соответствия выборочного распределениянормальному закону
Проверка сгруппированных данных
1. Группировка по интервалам
Формула Стерджесса
m 1 3.322 lg n
Проверка по критерию Пирсона
m
( N ti N эi )2
i 1
N ti
э2
2 , f m k 1
Проверка по критерию Колмогорова
D* max(| Fti Fэi |)
D D* ( N 0.01
0.85
N
)
44.
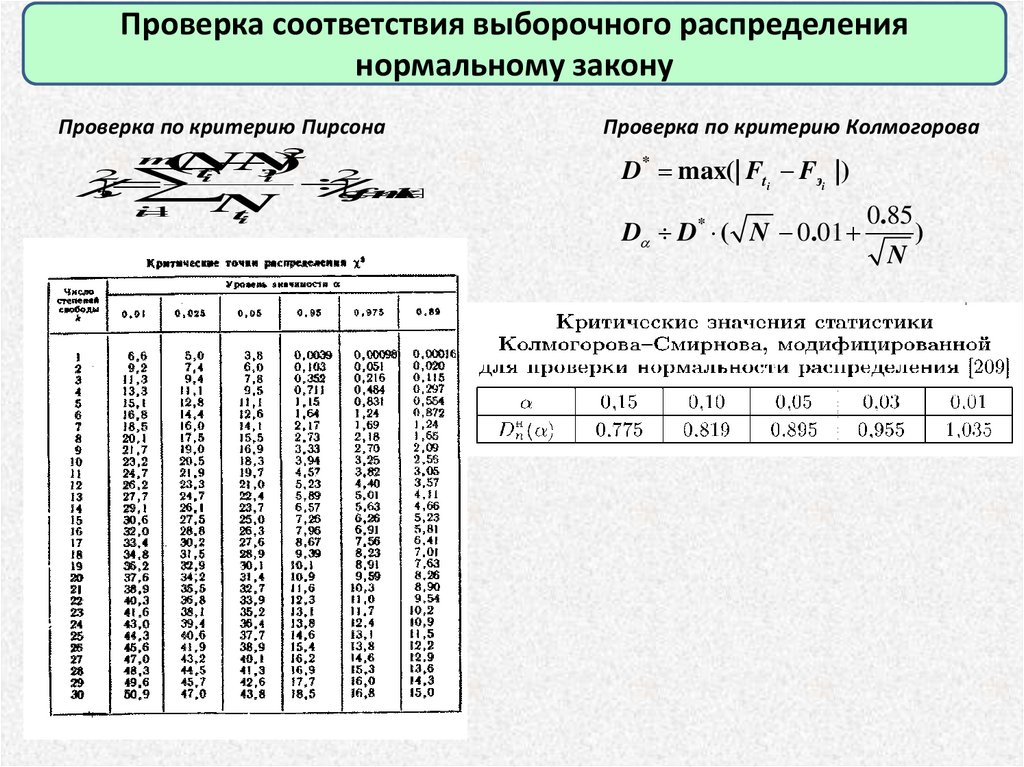
Проверка соответствия выборочного распределениянормальному закону
Проверка по критерию Пирсона
2
(
N
N
)
э
t
2
i
i
,fm
k
1
N
i
1
t
i
m
2
э
Проверка по критерию Колмогорова
D* max(| Fti Fэi |)
D D* ( N 0.01
0.85
N
)
45.
Проверка соответствия выборочного распределениянормальному закону
Тест Шапиро-Уилка
Если W<W( ), нулевая гипотеза отклоняется с вероятностью 1-
46.
Проверка соответствия выборочного распределениянормальному закону
Тест д’Агостино (K-квадрат
( x x)
A
,
3
i
n s3
Z1 a sinh(
A
6( n 2)
36 ( n 7)( n 2 2n 5)
, g1
( n 1)( n 3)
( n 2)( n 5)( n 7 )( n 9)
A
), 1
A
( x x ) 3,
E
4
i
n s4
E
ln W , 2 2 (W 2 1), W 2 2g 1 4 1
24n( n 2)( n 3)
6( n 2 5n 2) 6( n 3)( n 5)
, g2
2
( n 1) ( n 3)( n 5)
( n 7)( n 9) n( n 2)( n 3)
9Q
2
1 2 Q
8 2
1/ 3
1
Z2
(
) , Q 6 ( + 1 4 g 22 )
2 9Q 1 E 6 ( n 1) 2 (Q 4)
g2 g2
E
K 2 Z12 Z 2 2
47.
Проверка гипотезы об однородности двух независимыхвыборок
Проверка по t и F критериям
Sб2
F 2 Fa , f1 N ( sб ) 1, f 2 N ( sм ) 1
Sм
2
2
S
(
N
1
)
S
2
1
1
2 ( N 2 1)
Sun
N1 N 2 2
t
| X1 X 2 |
2
1
2
2
S
S
N1 N 2
t ta , f N1 N 2 2
;t
| X1 X 2 |
sun
1
1
N1 N 2
;
48.
Проверка гипотезы об однородности двух выборокПроверка по критерию Вилкоксона
{ x1 , x2 , ..., x N1 } { y1 , y2 , ..., y N 2 } общая выборка, ранжированная по возрастанию
W Rx
«Нулевая» гипотеза: Wн.кр. < W < Wв.кр
1. N1, N2 < 25, Wв.кр=(N1+N2+1)N1- Wн.кр
49.
Проверка гипотезы об однородности двух независимыхвыборок
Проверка по критерию Вилкоксона
2. N1 или N2 > 25
Wн.кр. (
( N1 N 2 1) N1 1
N1 N 2 ( N1 N 2 1)
(1 )
)
2
12
2
При наличии одинаковых рангов
m
(t t )
3
i
i
( N1 N 2 1) N1 1
N1 N 2 ( N1 N 2 1)
i 1
Wн.кр. (
(1 )
(1
)
2
2
12
( N1 N 2 ) 1)
2
Wв.кр=(N1+N2+1)N1- Wн.кр.
50.
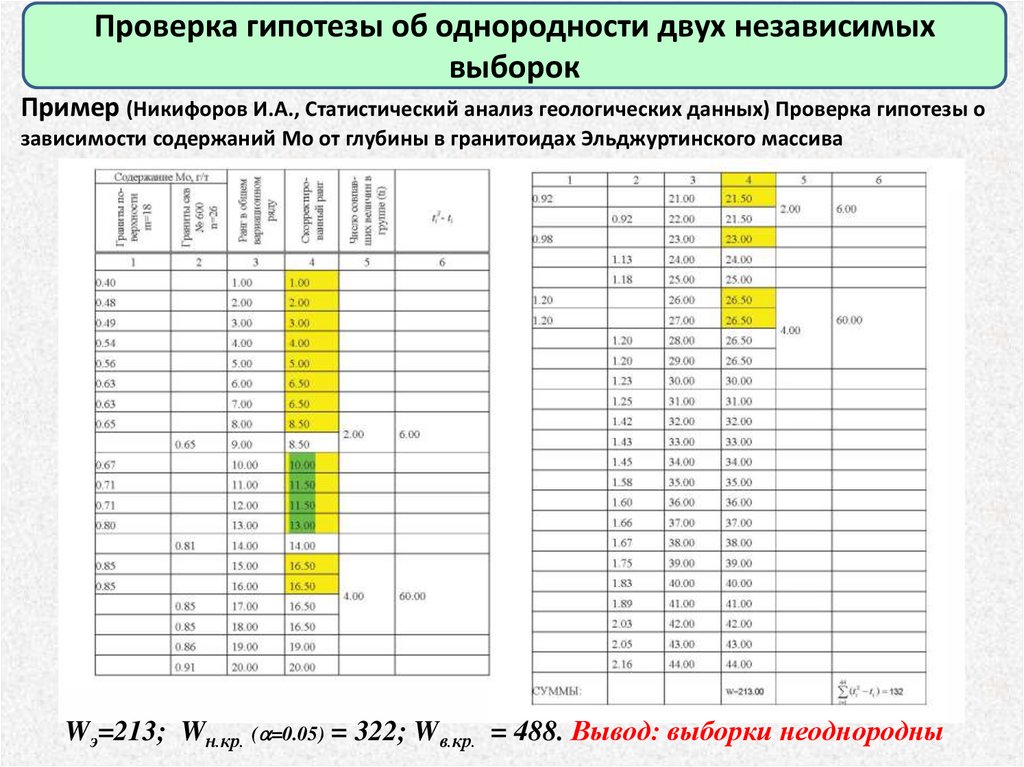
Проверка гипотезы об однородности двух независимыхвыборок
Пример (Никифоров И.А., Статистический анализ геологических данных) Проверка гипотезы о
зависимости содержаний Mo от глубины в гранитоидах Эльджуртинского массива
Wэ=213; Wн.кр. ( =0.05) = 322; Wв.кр. = 488. Вывод: выборки неоднородны
51.
Проверка гипотезы об однородности нескольких выборокОднофакторный дисперсионный анализ
Группы (уровни влияния фактора)
1
X11
X21
…
Xn11
2
X12
X22
…
Xn22
…
…
…
…
m
X1m
X2m
…
Xnmm
m
m
ni
SST ( X ij X общ ) ;
2
i 1 j 1
m
SS F ( X i X общ )2 ni ;
i 1
m
ni
SSe SST SS F ( X ij X i )2
i 1 j 1
N ni
i 1
SST
ST
;
N 1
SS F
SF
;
m 1
SSe
Se
N m
SF
FЭ
F ,m 1, N m
Se
52.
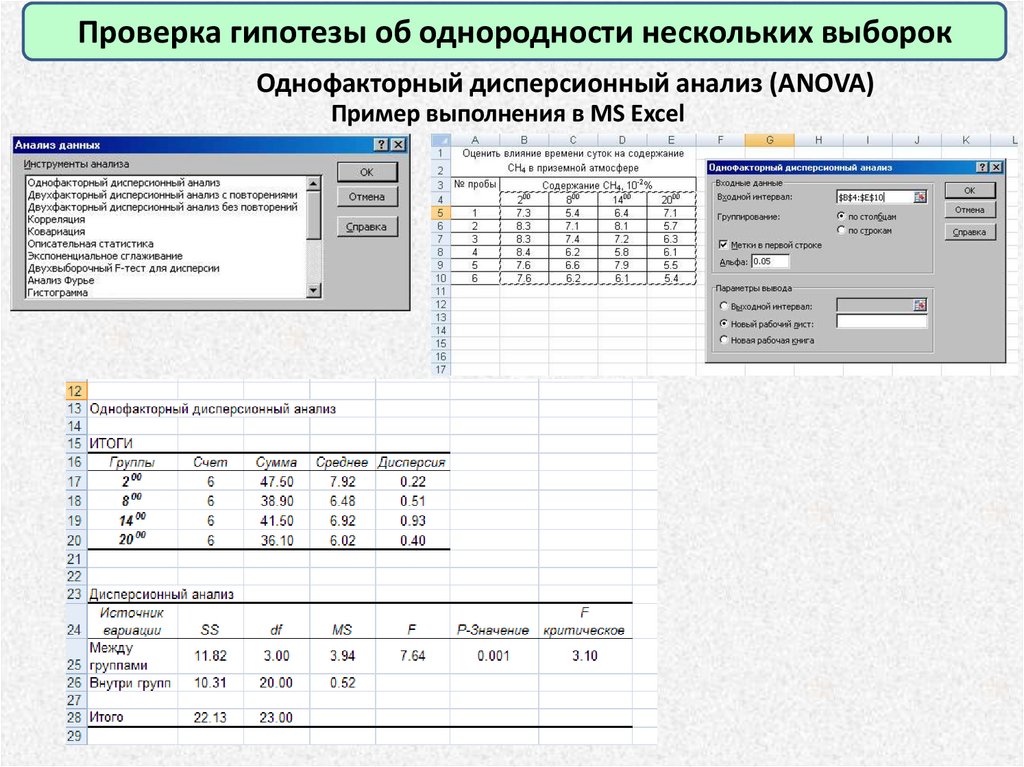
Проверка гипотезы об однородности нескольких выборокОднофакторный дисперсионный анализ (ANOVA)
Пример выполнения в MS Excel
53.
Проверка гипотезы об однородности нескольких выборокКритерий Краскела - Уоллиса
Группы
1
X11
X21
…
Xn11
2
X12
X22
…
Xn22
m
X1m
X2m
…
Xnmm
…
…
…
…
Сравниваются не сами значения, а их ранги в общей выборке.
m
nj
j 1
i 1
N n j ; S j Rij ; R j
Sj
R
N 1
; R
ij
nj
N
2
k
k S2
12
12
j
2
W
n j (Rj R)
3( N 1)
N ( N 1) j 1
N
(
N
1)
n
j 1
j
в случае совпадений берутся средние ранги, и
g
1
2
t
(
t
1), g число групп совпадений,
l
l
2
g
N ( N 1) l 1
tl количество совпадений ранго в каждой такой группе
W W ; g 1
/
Проверка для средних и малых выборок (статистика Имана-Дэвенпорта)
(N k)
W 0.5W (
1); W w 0.5( 1 ,k 1 (k 1) F1 ,k 1, N k )
N 1 W
54.
Проверка гипотезы об однородности нескольких выборокСравнение нескольких выборок по критерию -квардрат
Сравнивается k выборок, в каждой из которых m-уровней,
характеризующийся Nij наблюдениями (частотами попадания)
выборки
k
pj
1
N11
N21
…
Nk1
(N11+N21+…Nk1)/N
Интервалы
2
N12
N21
…
Nk2
(N12+N22+…Nk2)/N
…
…
…
…
m
N1m
N2m
…
Nkm
(N1m+N2m+…Nkm)/N
2
ˆ
(
N
N
p
)
i
j
Э2 ij
2 , f ( k 1) ( m 1)
N i pˆ j
i 1 j 1
k
m
k
N
ij
pˆ j i 1
N общ
k
m
N общ N ij
i 1 j 1
55.
Проверка гипотезы об однородности нескольких выборокПример. Проверить гипотезу о существовании связи между литологическим
составом речных галек и их формой
N 100
э2 12, 02.05, f 2 6
Вывод: различие значимое (на уровне 0.05)
56.
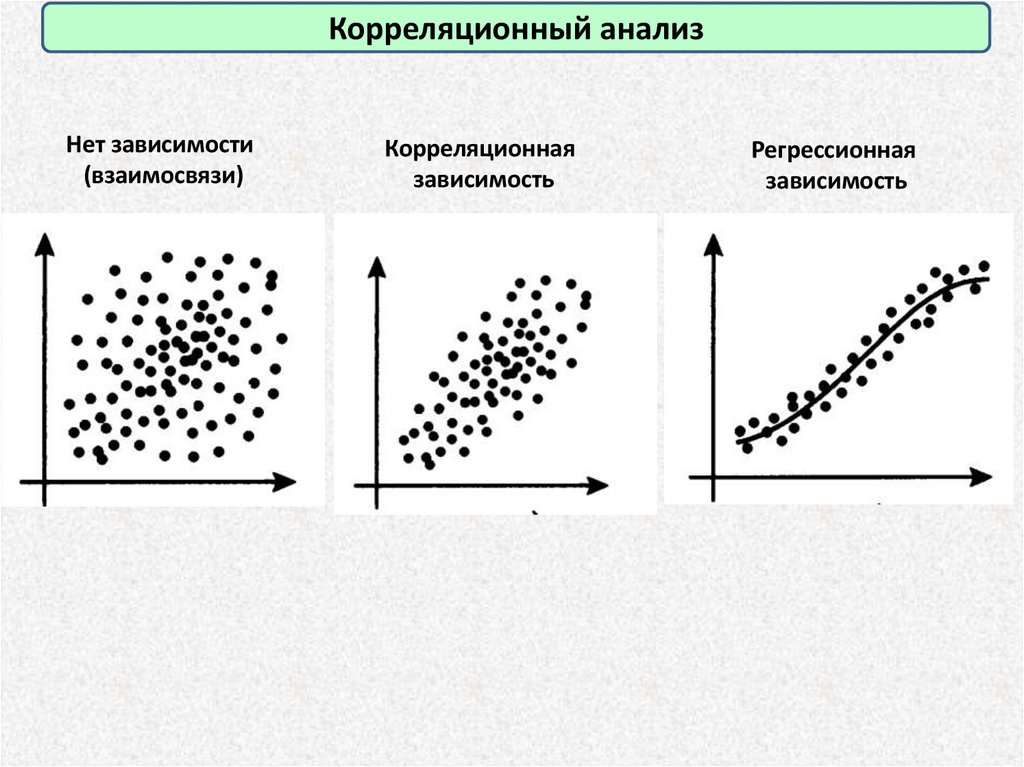
Корреляционный анализНет зависимости
(взаимосвязи)
Корреляционная
зависимость
Регрессионная
зависимость
57.
Корреляционный анализПарный корреляционный момент - ковариация
m xy M [( X M ( X )) (Y M (Y ))]
Свойства:
1. Мера совместной изменчивости
x y m xy x y
2. Мера совместной зависимости
m xy 0
m xy 0
58.
Корреляционный анализКоэффициент парной корреляции
m xy
xy
x y
Свойства:
1 xy 1
xy yx
Для независимых X,Y: xy = 0
Обратное утверждение не верно!
xy – мера линейной зависимости
59.
Корреляционный анализВыборочный коэффициент корреляции Пирсона
N
N
rxy
( x i x ) ( yi y )
i 1
s x s y ( N 1)
N
x y
i 1
N
i 1
x
y
i i
N
i
i 1
i
N
N
( xi 2
i 1
( xi )
N
2
i 1
N
N
) ( yi 2
i 1
( yi ) 2
i 1
N
)
Проверка значимости:
t , f N 2
N 2
| rxy |
t , f N 2 , либо: rxy r , f N 2
2
1 rxy
N 2 t 2 , f N 2
60.
Корреляционный анализВыборочный коэффициент корреляции Пирсона
Интервальная оценка:
z 0.5 ln
z1 z
1 rxy
Сравнение 2х коэффициентов:
1 rxy
1 a
N 3
; z2 z
e z1 e z1
r1 tanh( z1 ) z1
e e z1
e z2 e z2
r2 tanh( z2 ) z2
e e z2
1 a
z1 z2
2
N 3
;
1
1
N1 3 N 2 3
1
при 0.05, 1 1.96
2
2
61.
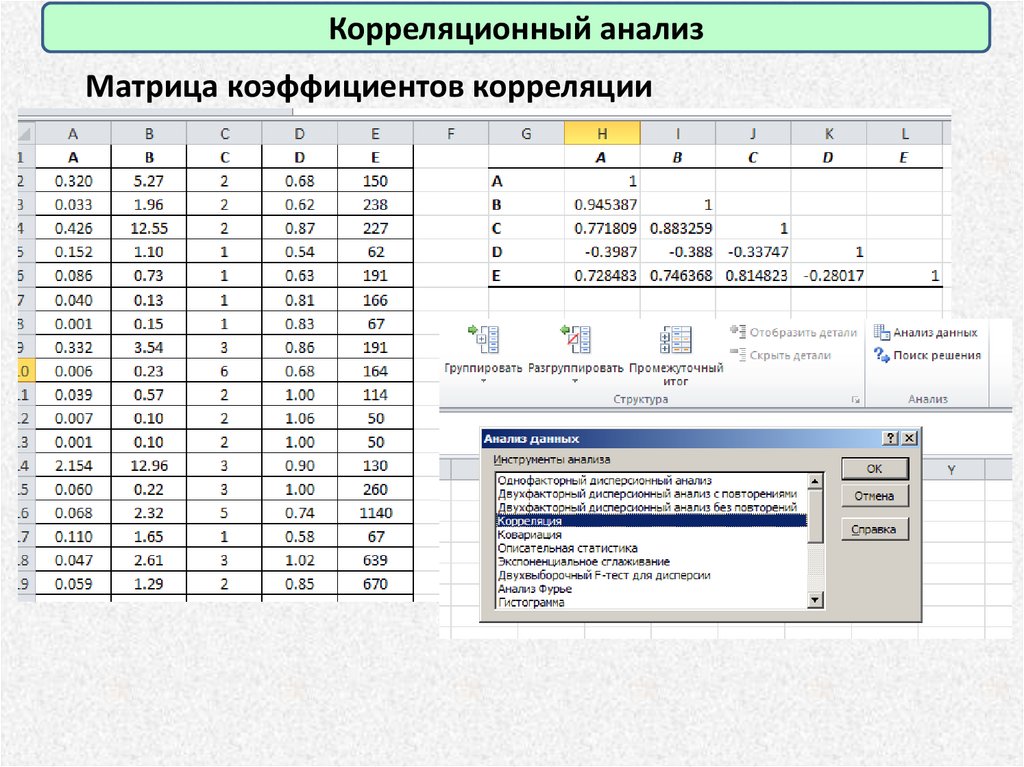
Корреляционный анализМатрица коэффициентов корреляции
62.
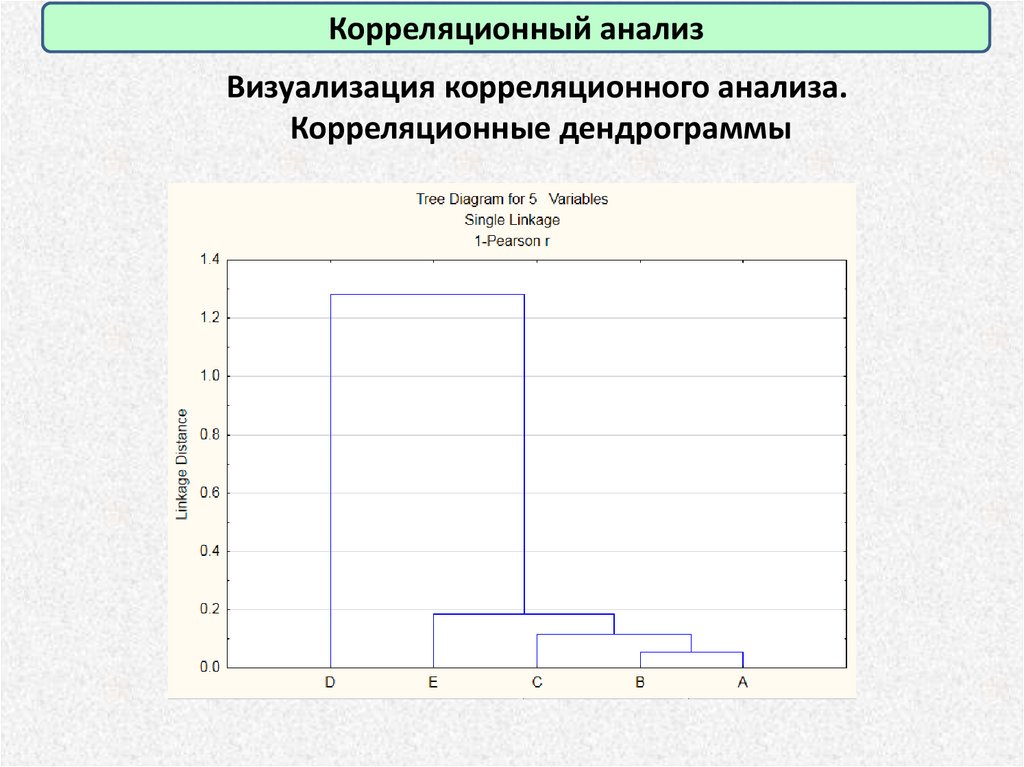
Корреляционный анализВизуализация корреляционного анализа.
Корреляционные дендрограммы
63.
Корреляционный анализРанговые коэффициенты корреляции
Коэффициент корреляции Спирмена
N
( Rx i Rx ) ( R yi R y )
xy i 1
sRx sRy ( N 1)
( ki3 k )
T
12
i 1
m
Проверка значимости:
N 2
| xy |
t , f N 2
2
1 xy
N
1
6 ( Rx i R yi ) 2
i 1
3
( N N ) 6 T
64.
Корреляционный анализРанговые коэффициенты корреляции
Коэффициент корреляции Кендалла
4R
xy 1
N ( N 1)
R – сумма «инверсий» (нарушений порядка расположения во 2-м ряду)
Проверка значимости:
xy Tкр
1
2
2( 2 N 5)
9 N ( N 1)
65.
Корреляционный анализЛожная корреляция
1.
«Влияние скрытого фактора»
Коэффициент частной корреляции
rxy , z
rxy rxz ryz
(1 rxz2 ) (1 ryz2 )
Мостеллер Ф., Тьюки Дж. Анализ данных и регрессия
Исследование в Великобритании во время 2-й Мировой войны зависимости точности
бомбометания Z от факторов: высота полёта бомбандировщика H, скорость ветра V,
количество истребителей X. Получалась неинтерпретируемая зависимость: Z имеет прямую
корреляцию с X. Объяснение: не учитывался фактор «Облачности»
Александров и др. Анализ данных на ЭВМ.
Прямая значимая корреляция между количеством новорожденных в сельской местности
Голландии и количеством прилетевших аистов. Объяснение: влияние колицества построенных
новых домов
66.
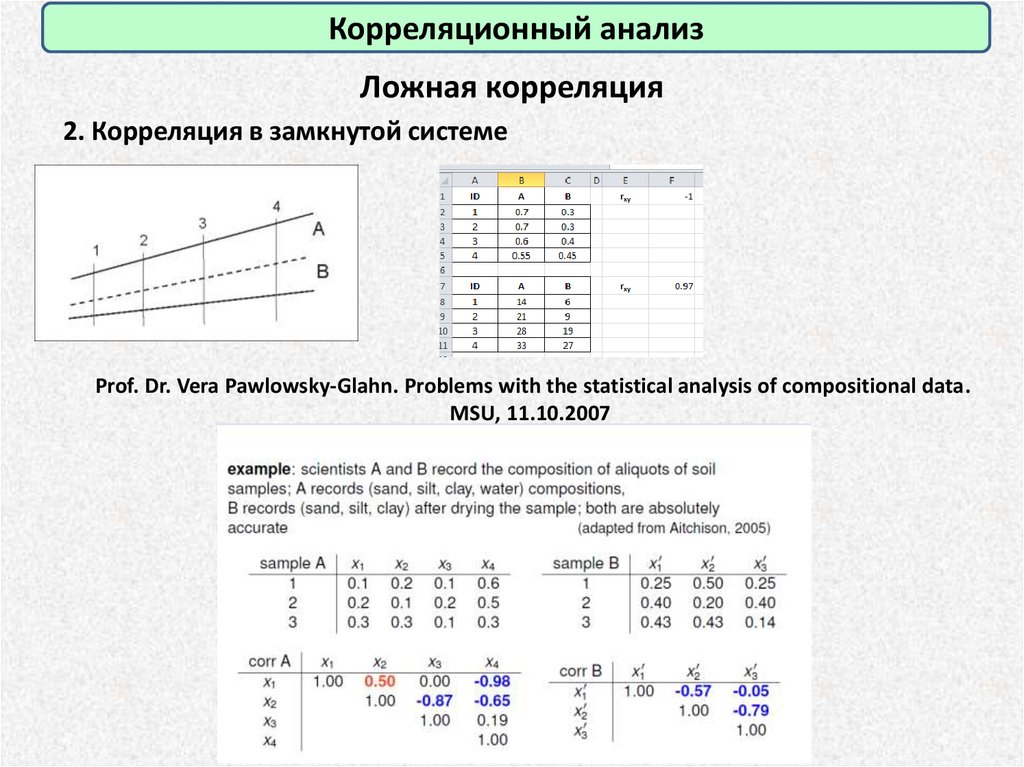
Корреляционный анализЛожная корреляция
2. Корреляция в замкнутой системе
Prof. Dr. Vera Pawlowsky-Glahn. Problems with the statistical analysis of compositional data.
MSU, 11.10.2007
67.
Регрессионный анализY=f(X1, X2, …, Xm)
Y
X
1.
2.
3.
4.
Термин «регрессия» ввел Ф. Гальтон в своей
статье «Регрессия к середине в наследовании
роста» (1885 г.), в которой он исследовал
зависимость среднего роста детей (Y) со
средним ростом их родителей (X). В работе
Гальтон показал, что зависимость Y от X хорошо
выражается уравнением: Y-Yср = (2/3)*(Х - Xср)
Общая последовательность регрессионного анализа:
Выбор вида зависимости;
Определение коэффициентов уравнения зависимости;
Оценка адекватности выбранной модели;
Оценка неизвестных значений Y.
68.
Регрессионный анализМетод наименьших квадратов (МНК)
y f ( x1 , x2 ...) e yˆ e
N
( yi yˆ ) min
2
i 1
Метод главных компонент (МГК)
69.
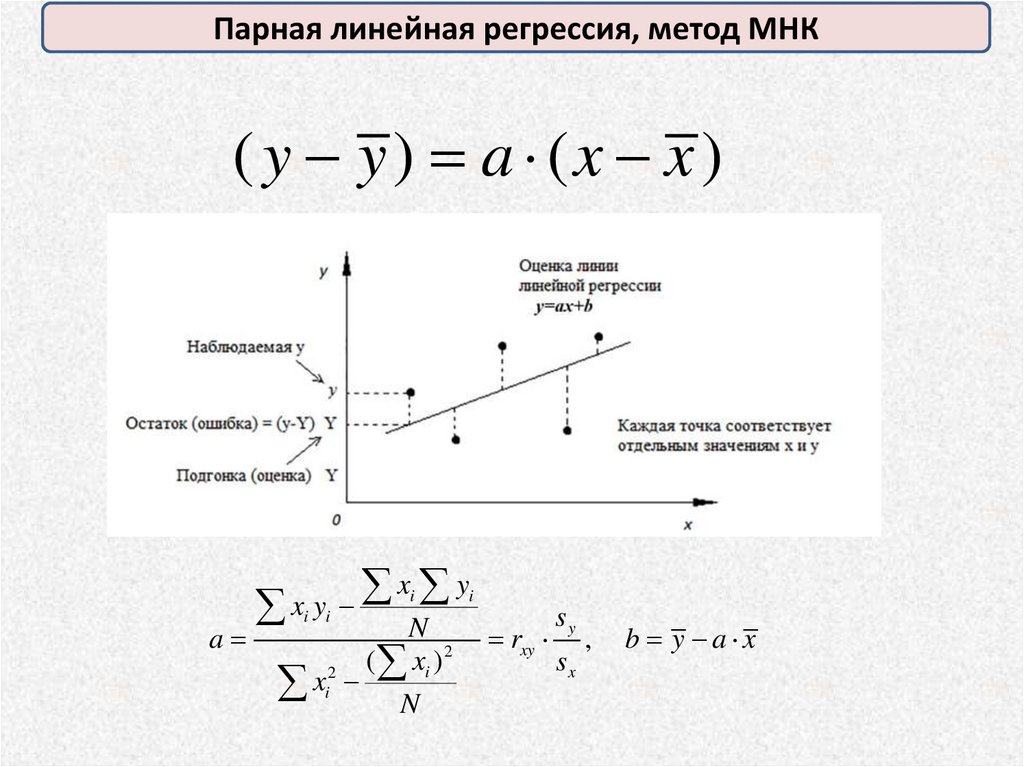
Парная линейная регрессия, метод МНК( y y) a (x x )
xi yi
x
y
ii
sy
N
a
rxy ,
2
( xi )
sx
2
xi N
b y a x
70.
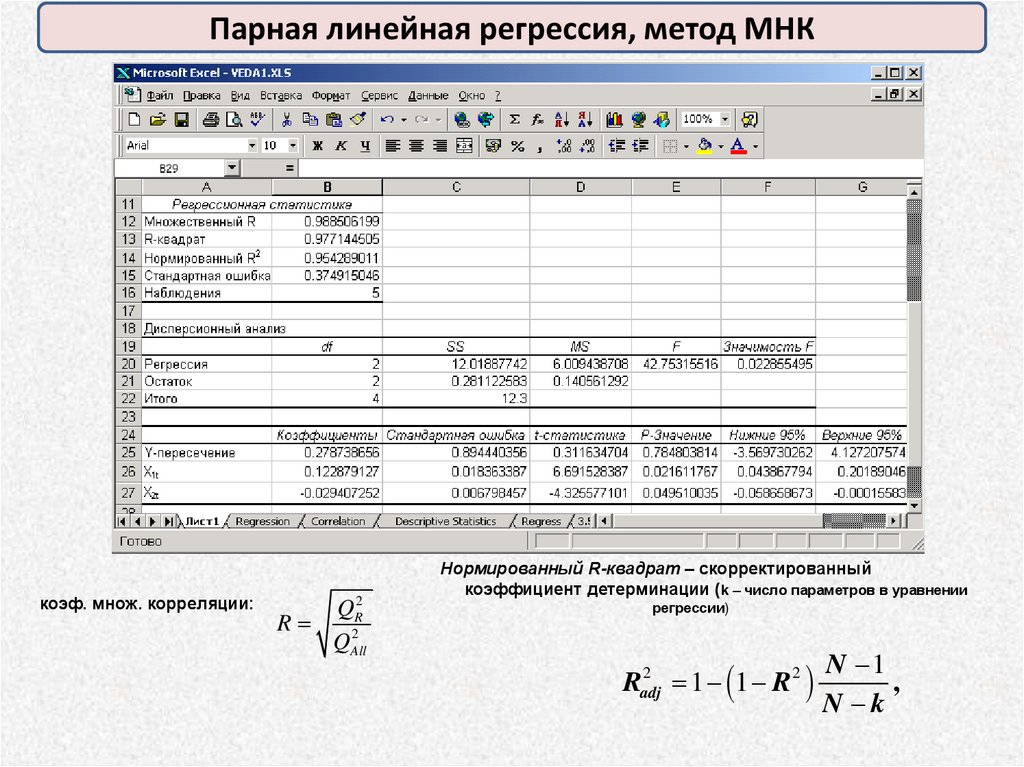
Парная линейная регрессия, метод МНКкоэф. множ. корреляции:
QR2
R
2
QAll
Нормированный R-квадрат – скорректированный
коэффициент детерминации (k – число параметров в уравнении
регрессии)
2
Radj
1 (1 R 2
N 1
,
N k
71.
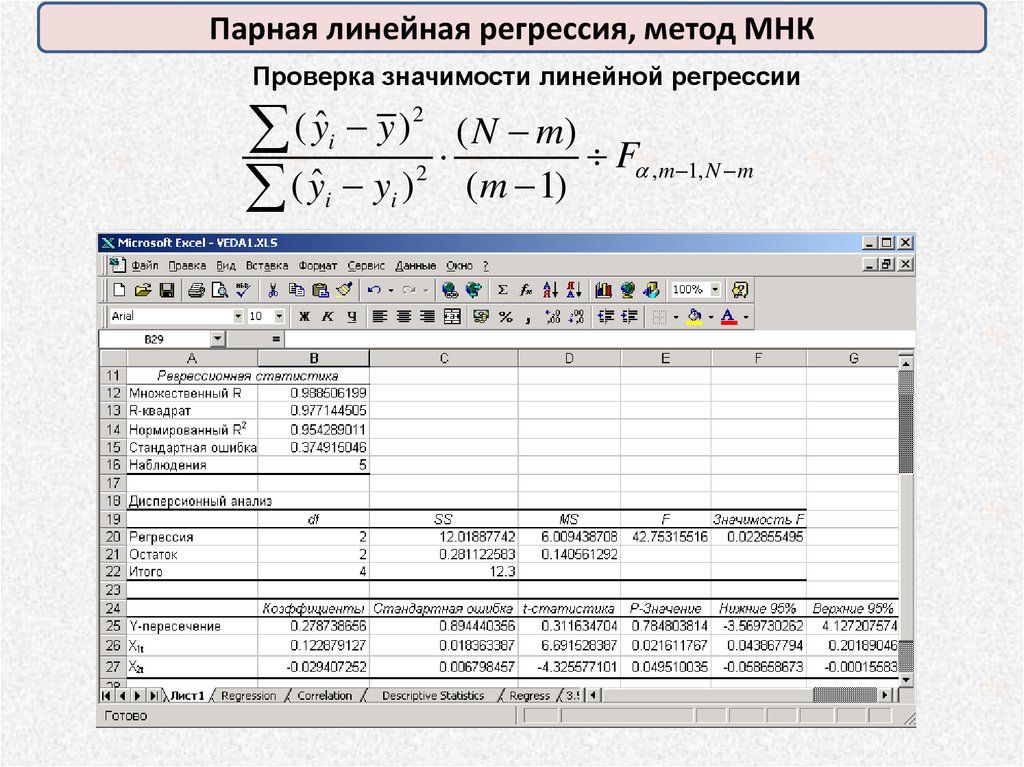
Парная линейная регрессия, метод МНКПроверка значимости линейной регрессии
2
ˆ
(
y
y
)
( N m)
i
F ,m 1, N m
2
( yˆi yi ) (m 1)
72.
Парная линейная регрессия, метод МНКПроверка значимости уравнения линейной регрессии
2
ˆ
(
y
y
)
/ ( k 1)
i
F ,k 1, N k
2
( yi yˆ i ) / ( N k )
Доверительные интервалы регрессионной оценки
yˆ 0 a x0 b, y0 yˆ 0 y 0 , s
( x0 x ) 2
1
y 0 t , N 2 s 1
N ( xi x ) 2
2
ˆ
(
y
y
)
i i
( N 2)
73.
Множественная линейная регрессияYt 0 1 X t ,1 2 X t ,2 ... k X t ,k t
e1
x1,m a0
e2
x2,m a1
...
... ...
...
xn ,m am
en
1 x1,1
1 x
2,1
Y X A E
... ...
1 xn ,1
...
...
...
...
метод МНК:
Для зависимости от 2-х переменных:
1
(X X ) X Y
T
T
(z z) A(x x) B( y y )
rxz ryz rxy sz
ryz rxz rxy sz
A
; B
2
2
(1 rxy )
sx
(1 rxy )
sy
Доверительные интервалы регрессионной оценки
y x t ,N m 1 se 1 x *T ( X T X ) 1 x *
74.
Множественная линейная регрессияТест на «короткую» и «длинную» регрессии (k переменных, или m
переменных):
F
( ESS R ESSUR / (k m) F
, k 1 m , N k 1
ESSUR / ( N k 1
Тест Чоу (на однородность регрессии)
F
( ESSunion ( ESS1 ESS2 ) / (k 1) F
, k 1, m n 2( k 1)
( ESS1 ESS 2 ) / ( m n 2 (k 1)
75.
Парадоксы регрессияЗависимость веса коровы (Z) от окружности туловища (X) и
расстояния от холки до хвоста (Y).
(Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика:
Исследование зависимостей. – М. Финансы и статистика, 1985)
Регрессионные модели:
1) линейная: Z a0 a1 X a2Y
2) степенная:
Z a0 X a1Y a2
3) «по смыслу»:
Z a0 X 2Y
Модель
1
2
3
Вся выборка
коэф.
s ESS ( N k )
a0 = -984.7
a1 = 4.73
a2 = 4.7
a0 = 0.0011
a1 = 1.556
a2 = 1.018
a0 = 1.13·10-4
25.9
24.5
26.6
По части наблюдений
Коэф. (для «тяжёлых
s (по выборке для
коров»)
«лёгких коров»)
a0 = 453.2
a1 = 0.62
a2 = -0.22
a0 = 266.4
a1 = 0.203
a2 = -0.072
a0 = 1.11·10-4
81
79
28
76.
Непараметрическая регрессияРобастные методы
Метод Тейла.
aˆ MED{( y j yi ) / ( x j xi ), 1 i j n},
ˆ i , i 1,..., n}
bˆ MED{ yi ax
77.
Анализ последовательностей данныхВременной ряд – последовательность наблюдений
некоторого признака (случайной величины) X, выполненных
через определенные промежутки времени (расстояния и
т.п.).
Тренд – неслучайное (упорядоченное изменение данных)
во временном ряде (последовательности данных).
X f (t )
78.
Анализ последовательностей данныхПроверка гипотезы о наличие линейного тренда
последовательности данных по критерию Аббе.
N
2
(
x
x
)
i
S i 1
N 1
Если:
N 1
2
(
x
x
)
i 1 i
; Q i 1
2( N 1)
Q
R R , N
S
принимаем гипотезу (с вероятностью 1- ) о наличии в
последовательности линейного тренда.
в
79.
Сглаживание (фильтрация) данныхФильтрация – методы преобразования исходных данных с
целью минимизации случайной составляющей («шума») при
условии сохранения неслучайной составляющей («полезного
сигнала»).
i
Линейная фильтрация «скользящими окнами».
k 1
2
x
xˆ i
k 1
j i
2
k
Расчёт крайних точек в последовательности по методу МНК:
k
k 1
k 1 k
x at b, t
, ..., 0, ...,
, t i t i3 0
2
2
i 1
i 1
x t
xt
xi t i
k
a
2
2
2
t
(
t
)
/
N
t
i i
i
i
i i
b x at x
i
j
80.
Анализ последовательностей данныхНелинейная фильтрация
Фильтр Шеппарда-Тодда.
фильтрация по 5 точкам
x a0 a1t a2 t 2
3 xi 2 12 xi 1 17 xi 12 xi 1 3 xi 2
xˆ i
35
Выбор длины фильтра
Размер фильтра не должен превышыть размер (период)
полезного (неслучайного) сигнала
81.
Анализ последовательностей данныхАвтокорреляция
Автокорреляционная функция – используется для
выявления периодичности в последовательности данных
(временном ряду)
N l
x x
N l
x x
rl
i 1
i
N l
i l
i 1
i
i 1
N l
N l
N l
( xi
2
i 1
( xi )2
i 1
N l
i l
N l
N l
) ( x i2 l
i 1
( xi l )2
i 1
N l
)
82.
Кластерный анализОбщая последовательность действий:
1.Нормировка
2.Расчёт «мер сходства»
3.Классификация
Нормировка:
xi/
xi/
xi/
( xi xmin )
( xmax xmin );
( xi x )
;
s
( xi MEDxi )
f ( x)
1
1 e axi
MAD
(MAD
1
MED{ xi MEDxi } ;
1.483
83.
Кластерный анализМеры сходства:
Метрика
•Симметрия: d(x,y) = d(y,x) 0;
•Неравенство треугольника: d(x,z) + d(y,z) d(x,y);
•Различимость нетождественных объектов: d(x,y) ≠ 0 ≡ x ≠ y;
•Неразличимость тождественных объектов: x = y ≡ d(x,y) = 0.
Метрики:
Евклидово расстояние:
dij
(x x )
il
2
jl
Манхэттэнское расстояние:
n
d ij xil x jl
l 1
Метрика Чебышева:
dij max( xil x jl )
Метрика Минковского
n
dij ( xil x jl ) p
l 1
p
1
84.
Кластерный анализТипы кластеров:
1. класс типа ядра (все расстояния между объектами в классе меньше
расстояния до других объектов)
2. кластер (сгущение в среднем: среднее расстояние между объектами в классе
меньше среднего между классами)
3. класс типа ленты
4. класс с центром
М.Б. Лагутин «Занимательная статистика»
85.
Кластерный анализКлассификация
Эвристические методы
метод k-средних
Иерархические методы
метод ближнего соседа
min min dij
метод дальнего соседа
max max dij
метод Уорда (Ward)
w
nk nl
2
xk xl
nk nl































































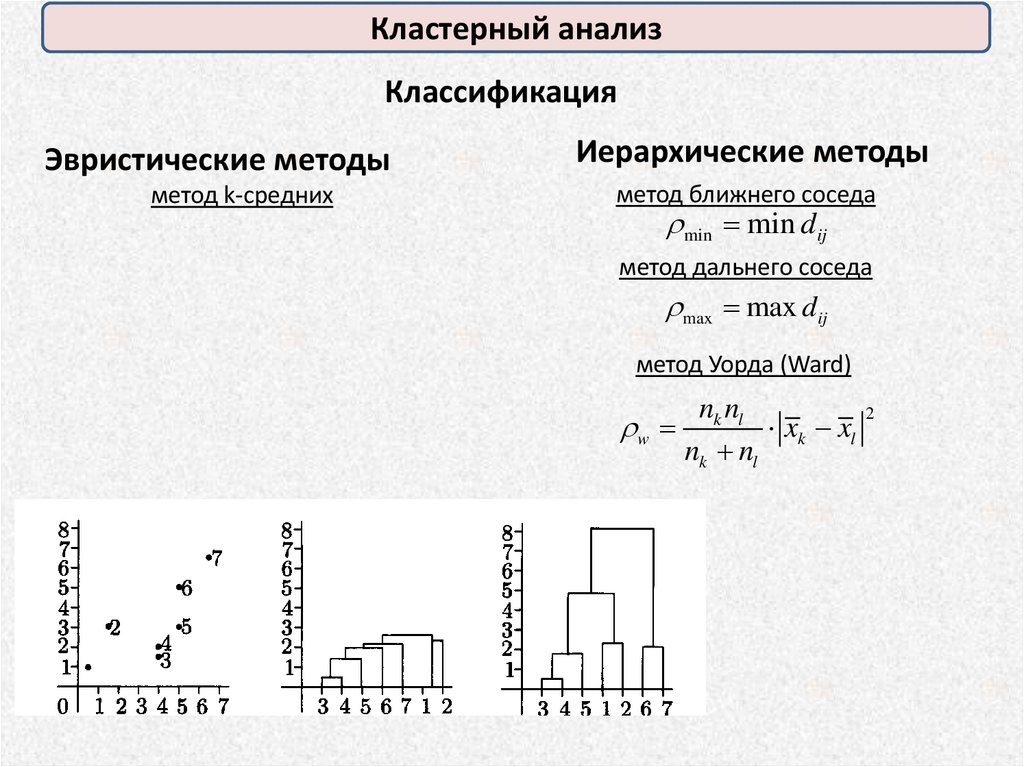
 mathematics
mathematics








