Дисциплина Статистические методы анализа данных

1. Дисциплина Статистические методы анализа данных

Кашникова Инна Васильевна
К. ф.-м.н, доцент
kashnikava@bsuir.by

2. Содержание учебного материала

• Тема 1. Первичная обработка статистических данных
• Тема 2. Числовые характеристики вариационных рядов
• Тема 3. Корреляционный анализ
• Тема 4. Регрессионный анализ
• Тема 5. Ряды динамики
• Тема 6. Кластерный анализ
• Тема 7. Дискриминантный анализ

3. Тема 1. Первичная обработка статистических данных

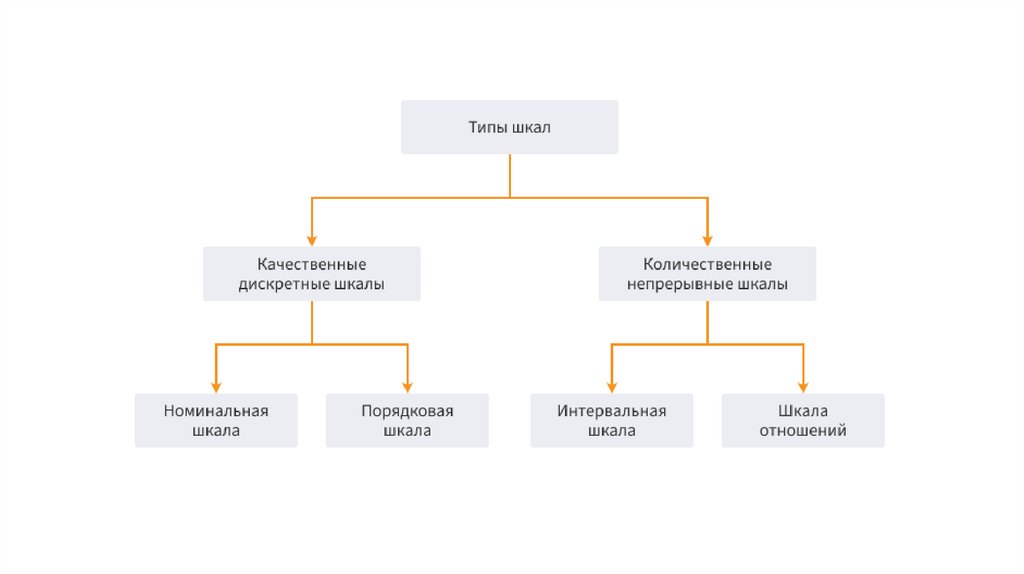
• 1. Введение
• 2. Типы статистических данных
• 3. Качественные и количественные шкалы
• 4. Выборочные наблюдения. Методы формирования выборки

4. 1. Статистические методы анализа данных.

Статистика изучает большие массивы информации и
устанавливает закономерности, которым подчиняются
случайные массовые явления.
Под математической статистикой понимается раздел
математики, посвященный математическим методам сбора,
систематизации, обработки и интерпретации статистических
данных.
Прикладная статистика – ориентированные на прикладную
деятельность статистические методы анализа реальных
данных, а также методологии организации статистических
исследований и их компьютерной обработки. Теоретическая
база – теория вероятностей и математическая статистика.
Анализ данных – позволяет подобрать информацию, которая
поможет ответить на все вопросы исследований и проверить
гипотезы.
4
4

5.

Статистические данные являются целью и результатом статистического
наблюдения,
и
представляют
собой
количественные
сведения
о
совокупностях элементов, выбранных в качестве единиц наблюдения. Все
множество этих единиц называется генеральной совокупностью, которая и
является объектом конкретного наблюдения.

6.

В основе статистического метода лежат закон больших чисел –
ЗБЧ и центральная предельная теорема – ЦБТ.
В соответствии с ЗБЧ при достаточном числе наблюдений
случайные
различия
отдельных
единиц
статистической
совокупности не влияют на общие закономерности.
ЦПТ объясняет характер распределения независимых случайных
величин, которое при увеличении числа испытаний стремится к
нормальному закону распределения.

7. Стадии статистического исследования

• Планирование и сбор данных
• Предварительное исследование
• Оценивание неизвестной величины
• Проверка статистических гипотез

8. Классификация статистических данных

по количеству переменных, описывающих
элементарную единицу данных:
по отношению ко времени:
• одномерные
• временные ряды
• многомерные
по типу измерения :
• количественные:
дискретные
непрерывные
• качественные:
порядковые
номинальные
• пространственные
по способу получения
данных:
• первичные
• вторичные

9.

10. Шкала наименований

= номинальная = классификационная
Примеры:
• имя, пол, семейство, класс,
номер игрока …
Обработка таблиц наблюдений:
• Неупорядоченный список класса
эквивалентных объектов
10

11. Порядковая шкала

= ранговая = ординальная
Примеры:
• ранг служащего, балльные шкалы (сила
ветра, оценка на экзамене, магнитуда
землетрясения, твердость минерала) …
Обработка таблиц наблюдений:
• Упорядочение объектов
• Ранг (порядковый номер) объекта
11

12. Интервальная шкала

= шкала разностей
Примеры:
• температура oC, oF, летоисчисление,
высота над уровнем моря …
Обработка таблиц наблюдений:
• Взятие интервалов – разностей
12

13. Шкала отношений

= метрическая
Примеры:
• длина, высота, вес, скорость, светимость
…
Обработка таблиц наблюдений:
• Арифметические операции
13

14.

Совокупность – группа объектов, предметов или явлений,
объединенных каким-либо общим признаком или свойством
качественной или количественной характеристики
(генеральная или выборочная совокупность).
Выборка или выборочная совокупность — часть генеральной
совокупности элементов, которая охватывается экспериментом
(наблюдением, опросом).
Характеристики выборки:
• Качественная характеристика выборки — что именно мы
выбираем и какие способы построения выборки мы для этого
используем.
• Количественная характеристика выборки — сколько случаев
выбираем, другими словами объём выборки.
Необходимость выборки:
• Объект исследования очень обширный.
• Существует необходимость в сборе первичной информации.
Заметим, что из генеральной совокупности можно отобрать огромное число
выборок. Например, при генеральной совокупности N, равной 100
элементам, можно извлечь выборки объемом n =10 в количестве 17·1012
вариантов (!).
14
14

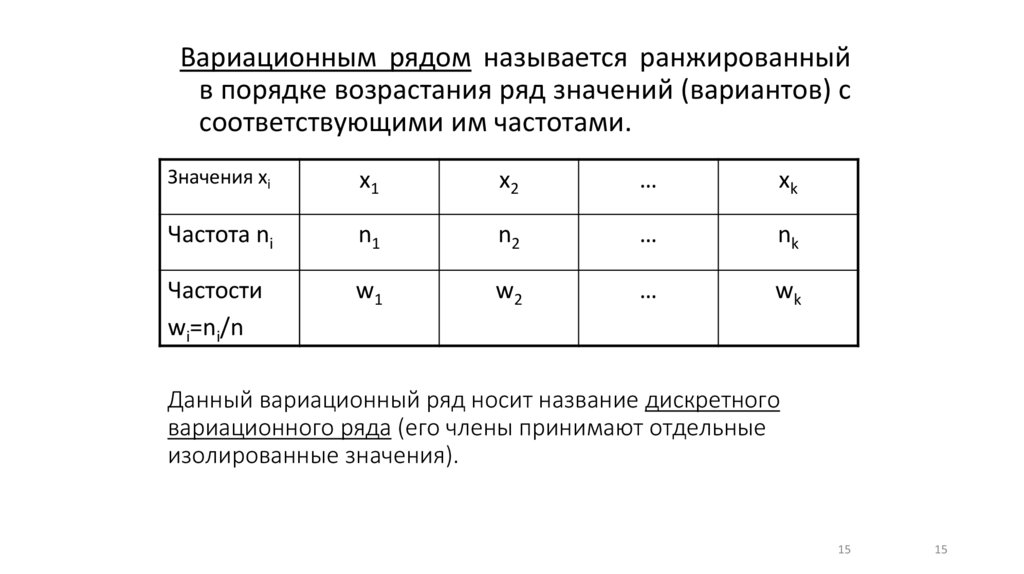
15. Данный вариационный ряд носит название дискретного вариационного ряда (его члены принимают отдельные изолированные значения).

Вариационным рядом называется ранжированный
в порядке возрастания ряд значений (вариантов) с
соответствующими им частотами.
Значения хi
x1
x2
…
xk
Частота ni
n1
n2
…
nk
Частости
wi=ni/n
w1
w2
…
wk
Данный вариационный ряд носит название дискретного
вариационного ряда (его члены принимают отдельные
изолированные значения).
15
15

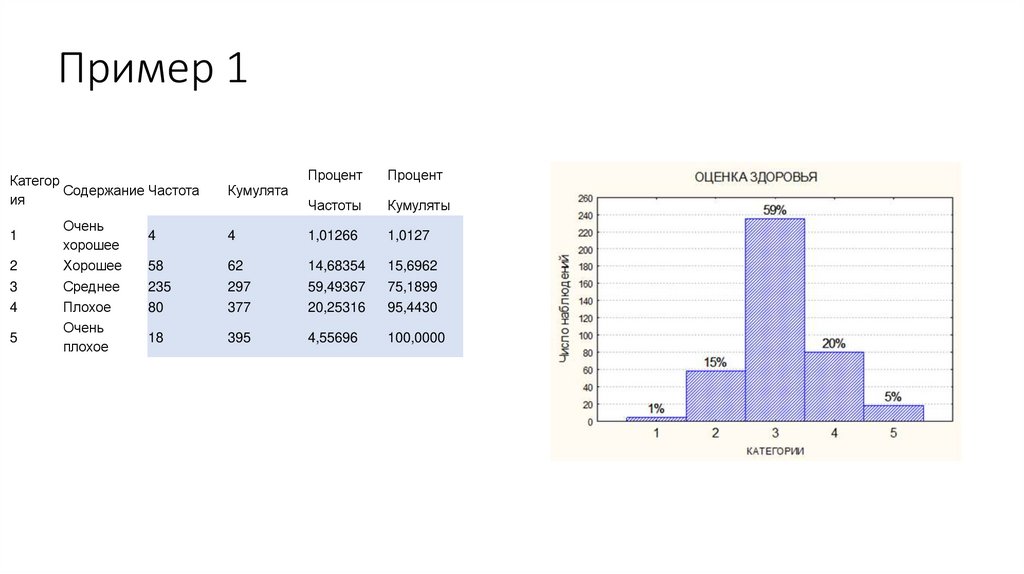
16. Пример 1

Категор
Содержание Частота
ия
1
2
3
4
5
Очень
хорошее
Хорошее
Среднее
Плохое
Очень
плохое
Кумулята
Процент
Процент
Частоты
Кумуляты
4
4
1,01266
1,0127
58
235
80
62
297
377
14,68354
59,49367
20,25316
15,6962
75,1899
95,4430
18
395
4,55696
100,0000

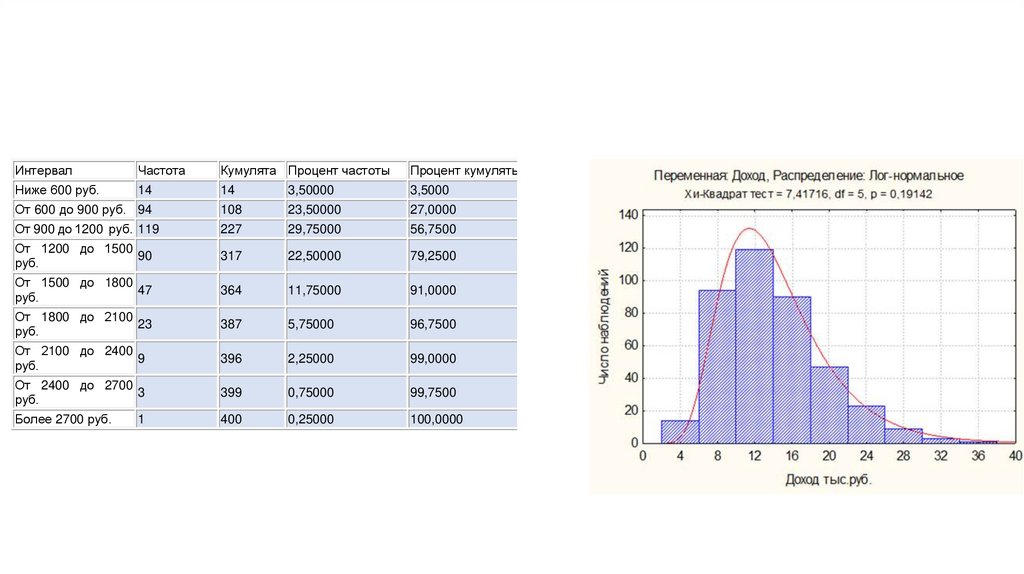
17.

Построение
дискретного
вариационного
ряда
нецелесообразно, когда число значений в выборке велико
или признак имеет непрерывную природу, т.е. может
принимать любые значения в пределах некоторого
интервала. В этом случае строят интервальный
вариационный ряд.
Вид интервального ряда:
Интервалы
вариантов
x1-x2
x2-x3
…
Xk-1-Xk
Частота ni
n1
w1
n2
w2
…
…
Nk-1
Wk-1
Частости
wi=ni/n
17
17

18.

Интервал
Частота
Кумулята Процент частоты
Процент кумуляты
Ниже 600 руб.
14
14
3,50000
3,5000
От 600 до 900 руб. 94
108
23,50000
27,0000
От 900 до 1200 руб. 119
227
29,75000
56,7500
От 1200 до 1500
90
руб.
317
22,50000
79,2500
От 1500 до 1800
47
руб.
364
11,75000
91,0000
От 1800 до 2100
23
руб.
387
5,75000
96,7500
От 2100 до 2400
9
руб.
396
2,25000
99,0000
От 2400 до 2700
3
руб.
399
0,75000
99,7500
Более 2700 руб.
400
0,25000
100,0000
1

19. Тема 2. Числовые характеристики вариационных рядов

1. Расчет средних значений, моды, медианы
2. Моменты к-го порядка
3. Построение гистограмм, кумулят частот, квартилей,
определение квантилей
4. Построение доверительных интервалов

20.

Пусть получена выборка объема n. Над этим массивом исходных данных
выполняется операция ранжирования, т.е. экспериментальные данные
выстраиваются в порядке возрастания:
x1 x2 x3 ... xk ;
причем
значение
k n;
xi
встречается
ni
раз :
n1 n2 ... nk n;
xi вариант;
ni частота
(количество
появлений
значений
xi );
ni
относительная
n
частота
варианта
wi
варианта
или
частость;
k
обязательно
выполняется
w 1;
i
i 1
размах
выборки
R xмах xmin xk x1.
20
20

21.

1. Средняя арифметическая
n
Х
х
i 1
- средняя арифметическая простая;
i
n
n
x f -
Х
i 1
n
f
n
X
i
i 1
x w
i 1
n
i
средняя
взвешенная;
арифметическая
i
i
w
i 1
i
i
- средняя арифметическая доли

22.

2 Средняя гармоническая
Средняя гармоническая – это величина, обратная
средней арифметической. Она применяется, когда
статистическая информация не содержит частот по
определенным
вариантам
совокупности,
представлена как их произведение.
X
n
n
1
i 1 xi
- средняя гармоническая простая;

23. 3 Средняя геометрическая

Средняя геометрическая величина используется также
для определения равноудаленной величины от
максимального и минимального значений признака.
Х x1 x2 ... xn
n

24. Структурные средние

Мода
наиболее часто повторяющееся значения признака
где ХMo - нижнее значение модального интервала;
mMo - число наблюдений или объем взвешивающего
признака в модальном интервале (в абсолютном либо
относительном выражении);
m Mo-1 - то же для интервала, предшествующего
модальному;
m Mo+1 - то же для интервала, следующего за модальным;
h - величина интервала изменения признака в группах

25. МОДА

• Распределение проданной женской обуви
по размерам характеризуется следующим
образом:
Размер
обуви
Количес
тво
проданн
ых пар
34
35
36
37
38
39
40
41
8
19
34
108
72
51
6
2

26.

Стаж лет
Число работников
До 2
4
2-4
23
4-6
20
6-8
35
8-10
11
Больше 10
7
Модальный интервал величины стажа 6-8 лет,
а мода продолжительности стажа:
Мо=6+2(35-20) / (35-20)+(35-11) = 6.77 года

27. Структурные средние

Медиана
величина признака, которая делит упорядоченную
последовательность его значений на две равные по
численности части
где XMe - нижняя граница медианного интервала;
hMe - его величина;
m/2- половина от общего числа наблюдений или половина
объема того показателя, который используется в качестве
взвешивающего в формулах расчета средней величины;
SMe-1 - сумма наблюдений (или объема взвешивающего
признака), накопленная до начала медианного интервала;
mMe - число наблюдений или объем взвешивающего признака
в медианном интервале

28. медиана

• В дискретном ряду распределения медиана
находится непосредственно по накопленной
частоте, соответствующей номеру медианы .

29.

•Дисперсия (S²) –
•Мера изменчивости для данных, полученных в метрических шкалах
(интервалов и отношений).
•Это характеристика отклонения от среднего. Она вычисляется по
формуле:
n
1
2
2
X i X
s
n 1 i 1

30.

• Стандартное отклонение
• Коэффициент вариации
• V<33%
выборка однородная

31. Начальные моменты

• Начальным моментом k k - го порядка случайной
величины X называется математическое ожидание k-й степени
этой случайной величины, т. е.
.
k M X
k

32. Начальные моменты

0 . M ( X 0 ) 1
1 . M ( X 1 ) M ( X )
• Если k = 0, то
• Если k = 1, то
2
2 . M ( X )
• Если
k = 2, то
• Т.о. математическое ожидание СВ есть начальный момент 1-го
порядка этой величины, а дисперсия может быть выражена через
начальные моменты 1-го и 2-го порядков:
.
D( X ) M ( X ) M ( X ) 2
2
2
2
1

33. Центральные моменты

• Центральным моментом k k-го порядка СВ X
называется математическое ожидание k-й
степени отклонения этой СВ от ее
математического ожидания, т. е.
математическое ожидание k-й степени
соответствующей центрированной СВ:
k M X M ( X ) M ,
• где
X.
k
k
– центрированное значение СВ
X M( X )

34. Центральные моменты

0 M ;( ) 1
0
• Если k = 0, то
• если k = 1,то
1 M ( ) M X M ( X )
1
1
;
M
(
X
)
M
(
X
)
0
• если k = 2, то
2
,
2 M X M ( X ) D( X )
• т. е. дисперсия СВ есть центральный момент
второго порядка этой величины:
• S2= D( X ) 2

35. Центральные моменты

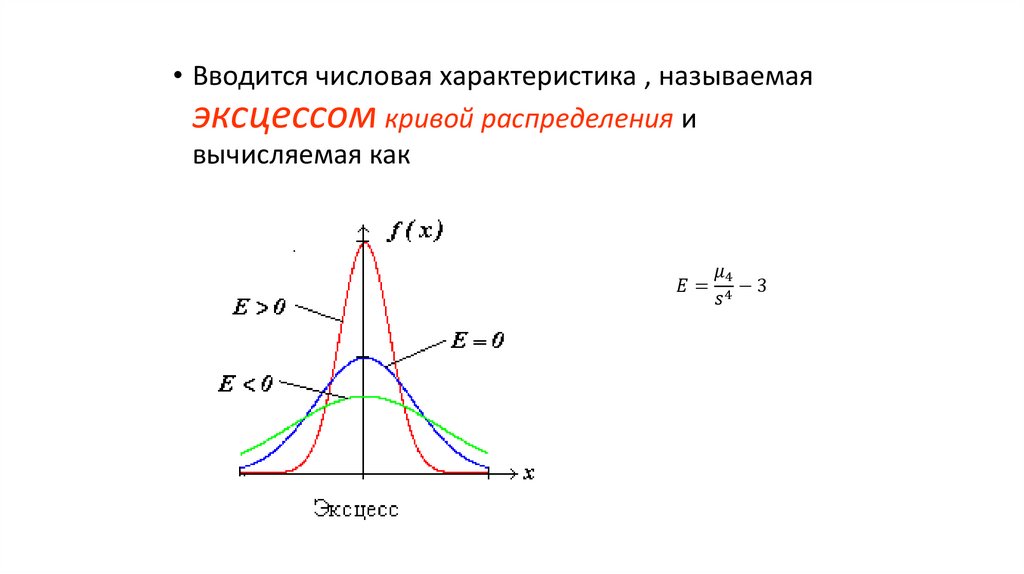
• Теоретически при симметричности кривой распределения все
центральные моменты нечетных порядков равны нулю, т.е.
2i 1 0 i 1,2,...,n
• Практически это свойство используется для характеристики
асимметрии (скошенности) кривой распределения.

36.

• Вводится коэффициент асимметрии А: