L3Sistema_statisticheskih_pokazatelej_v_BS

1. Абсолютные, относительные и средние величины

1. Понятие обобщающего статистического
показателя
2. Виды относительных величин
3. Средние величины

2.

Абсолютные обобщающие показатели - это число
единиц по совокупности в целом или по ее отдельным
группам, которое получают в результате суммирования
зарегистрированных значений признаков первичного
статистического материала.
Виды абсолютных величин
Индивидуальные
Суммарные
получают непосредственно в процессе
статистического наблюдения как
результат замера, взвешивания,
подсчета и оценки
характеризующие объем признака или
объем совокупности как в целом, так и по
какой-либо его части, получают в
результате сводки и группировки
индивидуальных значений: итоги
библиотечной деятельности, ресурсное обеспечение
(число читателей, выдачи документов, единиц
фонда)

3.

Единицы выражения абсолютных величин
Натуральные (число посещений за месяц)
Условно-натуральные (кормовые единицы, условное
топливо, условная пара обуви и др.)
Стоимостные (рубли, доллары, евро и др.)
Трудовые (человеко-часы, человеко-дни)

4. Виды относительных величин

5.

Относительный показатель (величина) - это
результат деления одного абсолютного показателя на
другой, выражающий соотношение между
количественными характеристиками социальноэкономических явлений и процессов.

6.

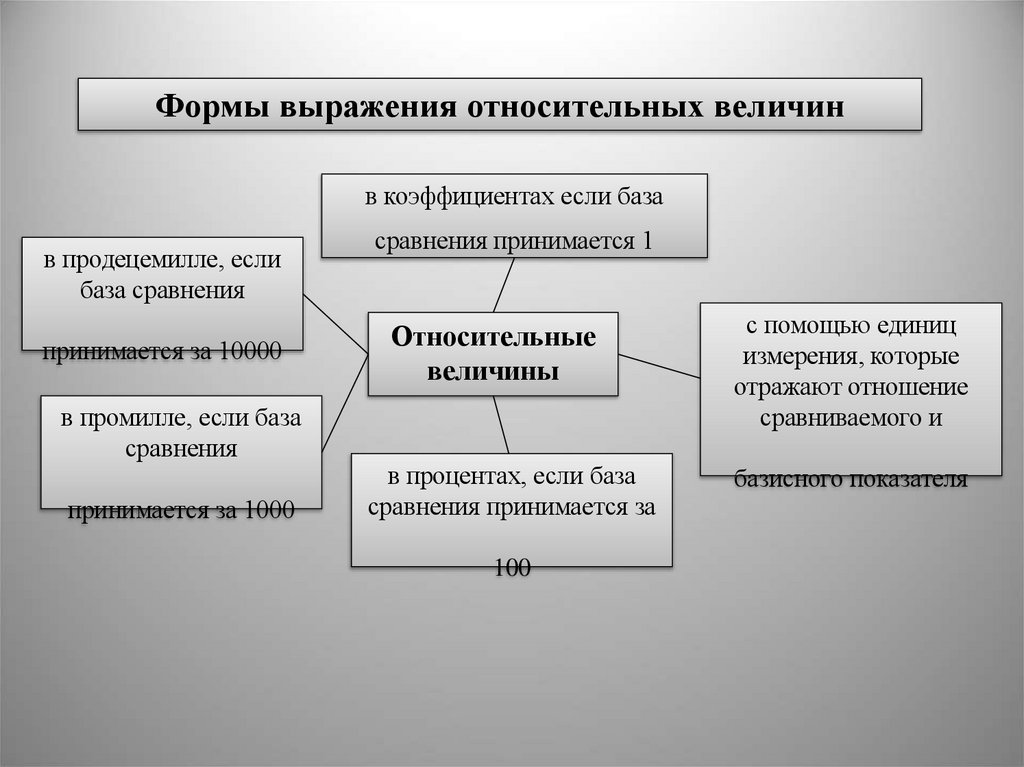
Формы выражения относительных величин
в коэффициентах если база
в продецемилле, если
база сравнения
принимается за 10000
в промилле, если база
сравнения
принимается за 1000
сравнения принимается 1
Относительные
величины
в процентах, если база
сравнения принимается за
100
с помощью единиц
измерения, которые
отражают отношение
сравниваемого и
базисного показателя

7.

Виды относительных величин
относительный показатель динамики - ОПД
относительный показатель структуры - ОПС
относительный показатель координации - ОПК
относительный показатель интенсивности - ОПИ
относительный показатель сравнения - ОПСр
относительный показатель плана - ОПП
относительный показатель реализации плана - ОПРП

8. Относительный показатель (величина) динамики

Показывает во сколько раз текущий уровень превышает
базовый

9. Относительный показатель (величина) структуры

Рассчитанные величины, называемые долями или
удельными весами, показывают, какой долей обладает или
какой удельный вес имеет та или иная часть в общем
итоге

10. Относительный показатель (величина) координации

Характеризует во сколько раз данная часть больше базисной,
или сколько % от нее составляет, или сколько единиц одной
части приходится на 1 (10, 100, 1000, 10000) единицу другой
части.

11. Относительный показатель (величина) сравнения

Представляет собой соотношение одноименных абсолютных
показателей, характеризующих разные объекты

12. Относительный показатель (величина) интенсивности

Получают, сопоставляя разноименные признаки одной
совокупности, а также объекты двух связанных между
собой совокупностей

13. Относительный показатель (величина) плана (относительный показатель планового задания)

Показывает во сколько раз намечаемый объем
производства превысит достигнутый уровень или
сколько % от этого уровня составит

14. Относительный показатель (величина) реализации плана (относительный показатель выполнения плана)

Отражает фактический объем производства в % или
коэффициентах по сравнению с плановым уровнем

15.

Читаемость = число книговыдач : число читателей.
Посещаемость = число посещений : число читателей.
Обращаемость = число книговыдач : объём фонда.
Книгообеспеченность читателя = объём фонда : число читателей.
Книгообеспеченность жителя = общий фонд библиотек территории : число
жителей.
Плотность библиотечной сети = число библиотек территории : число
жителей территории.
Доступность библиотечной сети = число жителей территории : число
библиотек.
Плотность и доступность характеризуют распространённость библиотечной
сети: чем больше библиотек на единицу территории или чем меньше
территория, приходящаяся на одну библиотеку, тем легче населению
пользоваться общественной книгой).

16. Средние величины

17. Средняя величина – обобщающий показатель, который дает количественную характеристику признака в статистической совокупности в

условиях
конкретного места и времени

18.

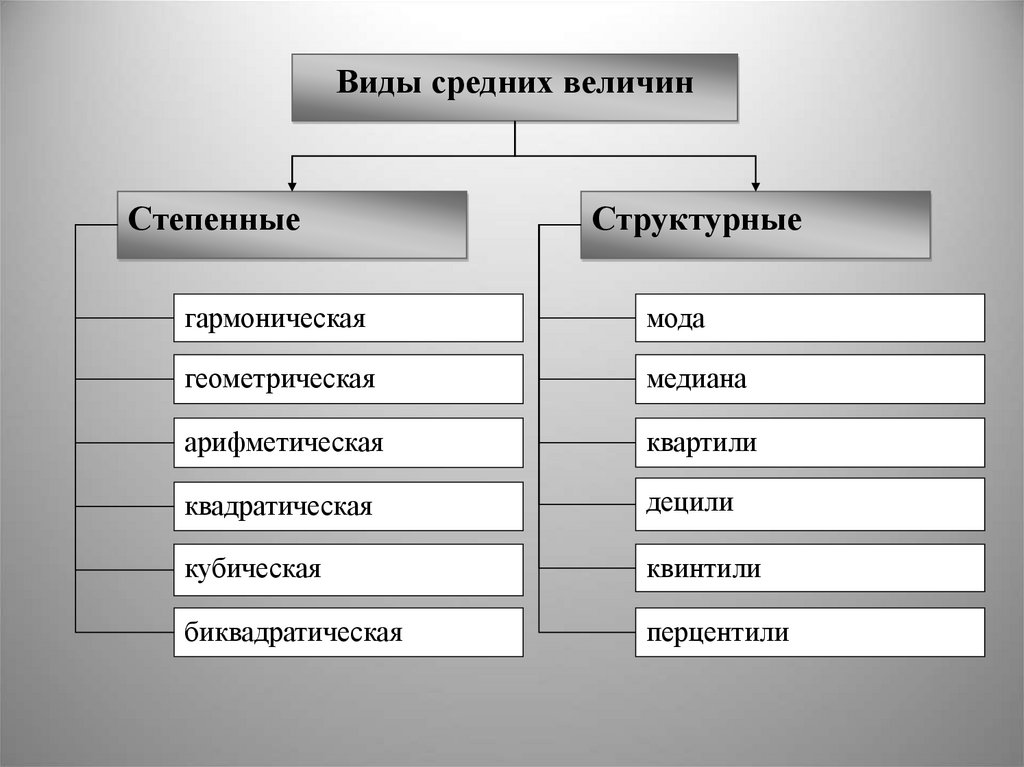
Виды средних величин
Степенные
Структурные
гармоническая
мода
геометрическая
медиана
арифметическая
квартили
квадратическая
децили
кубическая
квинтили
биквадратическая
перцентили

19.

Средняя арифметическая (k=1) исчисляется в тех случаях,
когда объем варьирующего признака для всей совокупности
образуется как сумма значений признака отдельных ее единиц.
средняя арифметическая
простая
средняя арифметическая
взвешенная

20.

Мода представляет собой значение изучаемого признака,
повторяющееся с наибольшей частотой.
В дискретном ряду мода – это варианта с наибольшей частотой.
В интервальном ряду используют следующую формулу:
- нижняя граница модального интервала
- величина модального интервала
- частота модального интервала
- частота следующая за модальным интервалом
- частота предшествующая модальному интервалу

21.

Медианой называют значение признака, приходящееся на
середину упорядоченной (ранжированной) совокупности.
В дискретном ряду медиана с нечетным числом членов
является варианта, расположенная в центре ряда.
В интервальном ряду используется следующая формула:
- начальное значение медианного интервала
-величина модального интервала
-сумма частот ряда
- накопленная частота интервала предшествующая
медианному интервалу
- частота медианного интервала

22. Показатели вариации

23.

Вариация признака - это различие индивидуальных значений
признака внутри изучаемой совокупности, т.е. колеблемость,
многообразие, изменяемость величины признака у отдельных
единиц совокупности
Показатели вариации
Абсолютные показатели:
размах вариации
среднее линейное отклонение
дисперсия
среднее квадратическое
отклонение
Относительные показатели:
коэффициент вариации
коэффициент осцилляции
линейные коэффициент вариации

24.

Размаха вариации – характеризует границы вариации
изучаемого признака
Xmax и Xmin - наибольшее и наименьшее значения варьирующего
признака
Показывает, на сколько велико различие между единицами
совокупности, имеющими самое маленькое и самое большое
значение признака. Показатель основан на крайних значениях
варьирующего признака и не отражает отклонений всех
вариант в ряду.

25.

Среднее линейное отклонение есть средняя арифметическая
из абсолютных значений отклонений отдельных вариантов от
их средней величины
для не сгруппированных данных
для сгруппированных данных
xi - значение признака в дискретном ряду или середина интервала в интервальном
распределении;
fi - частота признака.
Среднее линейное отклонение выражено в тех же единицах
измерения, что и варианты или их средняя. Оно дает
абсолютную меру вариации. Показывает, на какую величину
отклоняется признак в изучаемой совокупности от средней
величины признака.

26.

Дисперсия представляет собой средний квадрат отклонений
индивидуальных значений признака от их средних величин.
для несгруппированных
данных
для сгруппированных
данных
Расчет дисперсии может быть упрощен.
или

27.

Среднее квадратическое отклонение измеряется в тех же
единицах, что и варьирующий признак, и исчисляется путем
извлечения квадратного корня из дисперсии
для несгруппированных данных
для сгруппированных данных
показывает, на сколько в среднем отклоняются конкретные
варианты признака от его среднего значения

28.

Коэффициент вариации – характеризует меру вариации
значений признака вокруг средней величины
Чем коэффициент меньше, тем однороднее совокупность и
наоборот, чем больше тем неоднороднее

29.

Линейный коэффициент
вариации
Коэффициент осциляции
или