Дробный факторный эксперимент. Метод ортогонального центрального композиционного планирования

1. Лекция 2

Дробный факторный эксперимент.
Метод ортогонального центрального
композиционного планирования. Метод
ротатабельного планирования.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Метод ортогонального центрального
композиционного планирования
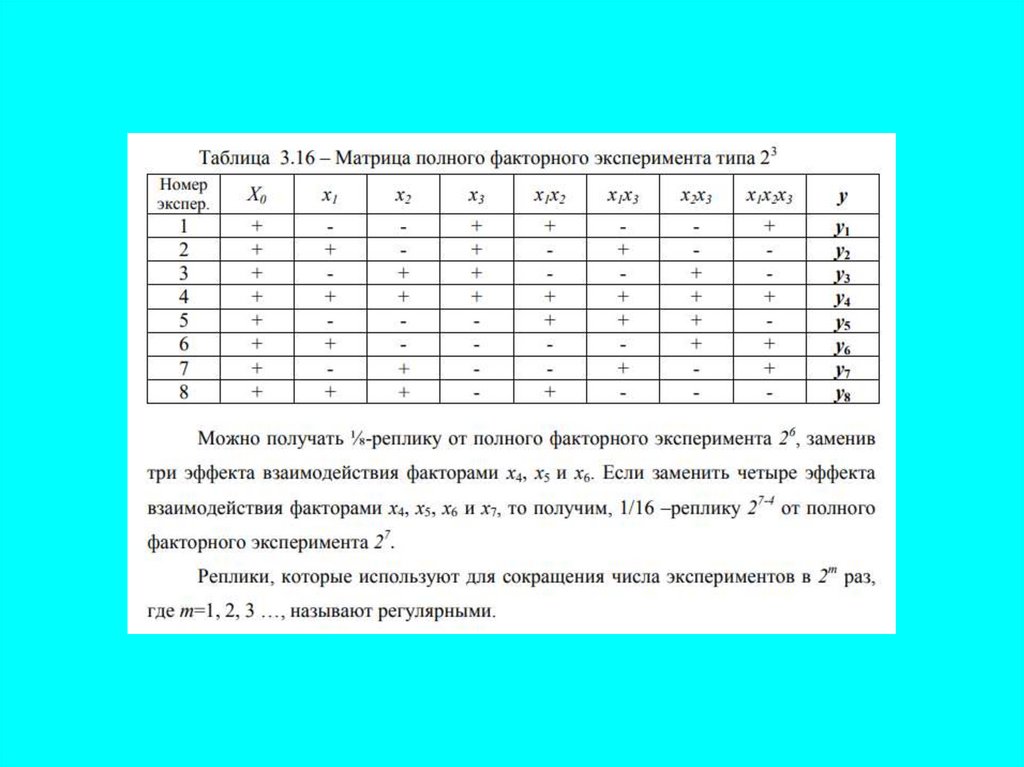
В том случае, когда поверхность отклика не может быть описана многочленом вида (2.9), для
адекватного математического описания используется многочлен более высокой степени,
например, отрезок ряда Тейлора (2.5), содержащий члены с квадратами переменных. С этой
целью используют центральное композиционное планирование эксперимента (ЦКП). Различают
два вида ЦКП: ортогональное и ротатабельное.
Количество опытов при ортогональном ЦКП определяется по формуле
где 2n – количество опытов, образующих полный факторный эксперимент;
2n – число так называемых «звездных» точек в факторном пространстве, имеющих координаты
(±α, 0, 0, ..., 0); (0, ±α, 0, ..., 0), ..., (0, 0, ..., ±α). Здесь величина α называется «звездным» плечом; 1
– опыт в центре планирования, т. е. в точке факторного пространства с координатами (0, 0, ..., 0).
Если с помощью полного факторного эксперимента не удается получить адекватного
математического описания в форме (2.9), то к нему добавляют опыты в «звездных» точках и в
центре плана, а полученную при этом композицию используют для получения математического
описания процесса в виде многочлена второй степени. Отсюда и произошло название метода:
центральное композиционное планирование.
Значения «звездного» плеча α для ЦКП с различным числом факторов п следующие:

11.

Эти значения α выбраны из условия ортогональности матрицы планирования.
Уравнение регрессии при ортогональном ЦКП ищут в следующем виде:
Переменные величины
введены для того, чтобы матрица планирования была ортогональна и коэффициенты
регрессии определялись независимо друг от друга по результатам опытов.
Для того, чтобы получить уравнение регрессии в обычной форме
находят величину
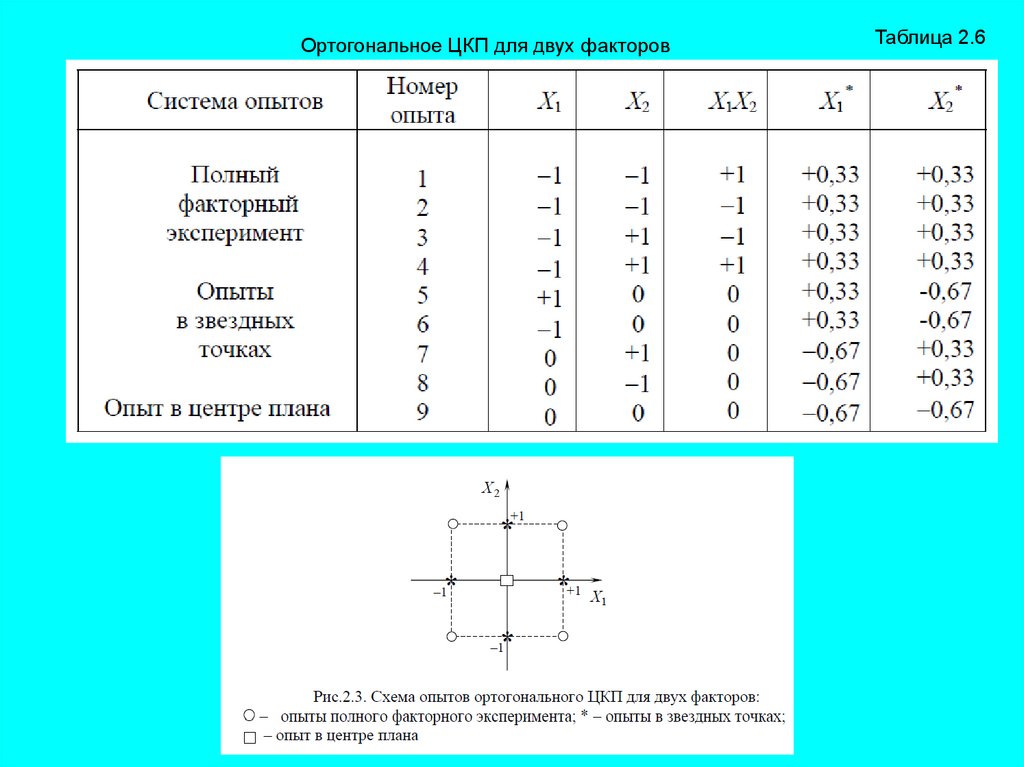
В табл. 2.6. приведена в качестве примера матрица ортогонального ЦКП для
двух факторов, а на рис. 2.3 изображена схема этих опытов.

12.

Ортогональное ЦКП для двух факторов
Таблица 2.6

13.

Коэффициенты регрессии при ортогональном ЦКП рассчитываются по следующим формулам:
Для расчета оценок дисперсий в определении коэффициентов регрессии используют следующие
выражения:

14.

Коэффициент bi, считается значимым, если
Аналогично проверяется значимость остальных
коэффициентов регрессии. Проверка адекватности
уравнения регрессии осуществляется с помощью критерия
Фишера (2.18).

15.

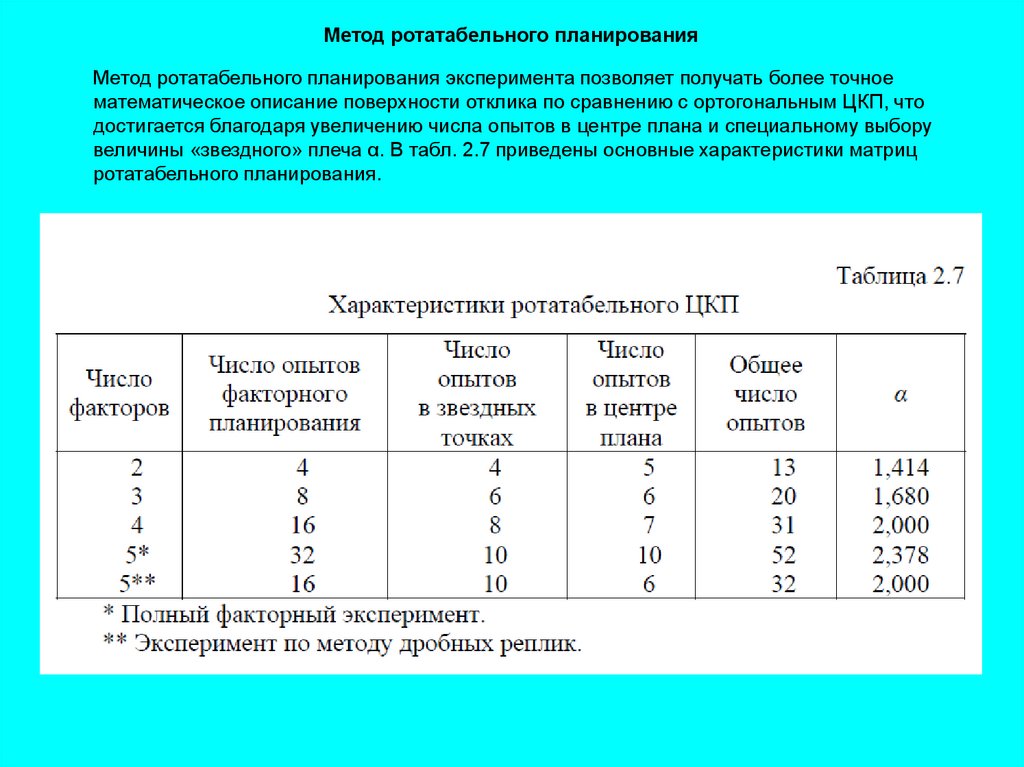
Метод ротатабельного планирования
Метод ротатабельного планирования эксперимента позволяет получать более точное
математическое описание поверхности отклика по сравнению с ортогональным ЦКП, что
достигается благодаря увеличению числа опытов в центре плана и специальному выбору
величины «звездного» плеча α. В табл. 2.7 приведены основные характеристики матриц
ротатабельного планирования.

16.

При ротатабельном планировании второго порядка достраивают план ПФЭ или его
регулярную дробную реплику (обычно полуреплику) до плана второго порядка
добавлением к “ядру” определенного количества “звездных” и нулевых точек. Матрицу
ПФЭ рекомендуется использовать в качестве “ядра” ротатабельного плана второго
порядка при к < 5, а полуреплику при к > 5. “Звездные” точки строят на осях координат,
определяя величину “звездного” плеча со (расстояния от нулевой точки до “звездной” по
оси координат); при этом принимается во внимание условие ротатабельности (для “ядра” в
виде плана ПФЭ):

17.

При ротатабельном ЦКП для вычисления коэффициентов регрессии и соответствующих оценок дисперсий находят следующие константы:
где n – число факторов; N – общее число опытов ротатабельного ЦКП; N0 – число
опытов в центре плана.
На основании результатов эксперимента вычисляют следующие суммы:

18.

Формулы для расчета коэффициентов регрессии имеют следующий вид:
Оценки дисперсий в определении коэффициентов регрессии вычисляют по
следующим формулам:

19.

В ротатабельном ЦКП принято считать, что коэффициент bi значим, если
Аналогичные условия значимости справедливы и для других коэффициентов регрессии.
Оценку дисперсии адекватности рассчитывают по формуле
С ней связано число степеней свободы:
Проверку адекватности уравнения регрессии осуществляют с помощью критерия Фишера.
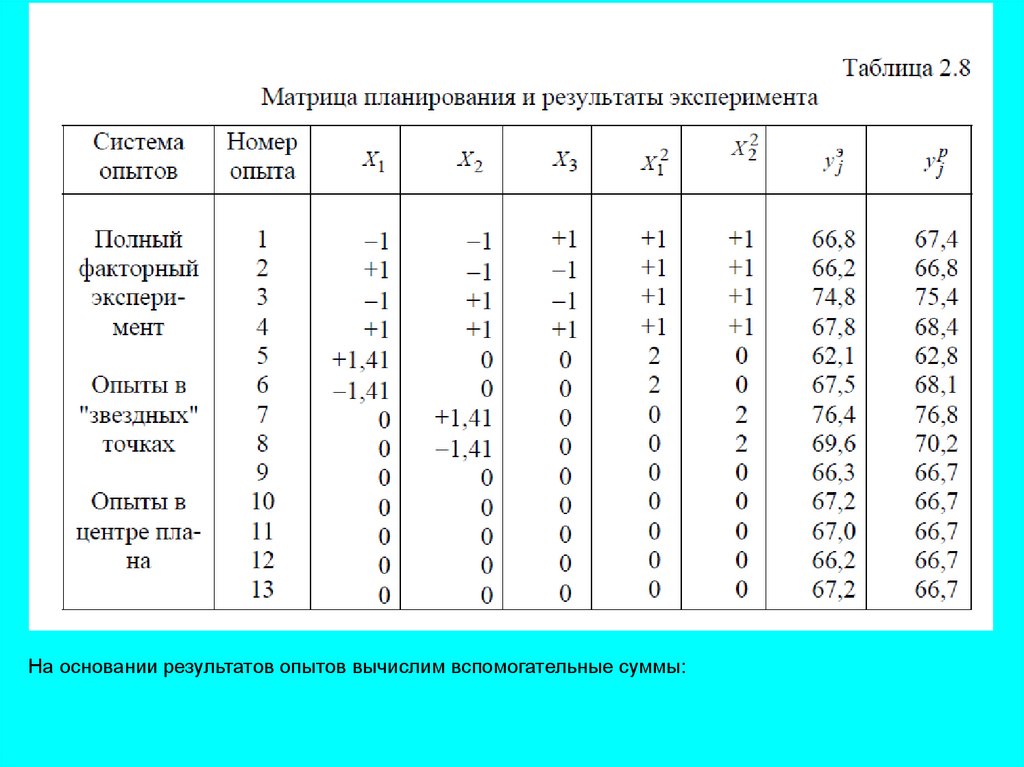
Пример. Рассмотрим ротатабельное ЦКП для двух факторов. Матрица планирования и
результаты эксперимента приведены в табл. 2.8.
Для нахождения коэффициентов регрессии вычислим следующие вспомогательные
коэффициенты:

20.

На основании результатов опытов вычислим вспомогательные суммы:

21.

Коэффициенты регрессии рассчитываем по формулам (2.43) — (2.46):

22.

Оценку дисперсии воспроизводимости можно найти на основании
результатов опытов, проведенных в центре плана.
Для этого вычислим:

23.

тогда
Эта величина найдена нами при числе степеней свободы
Оценки дисперсий в определении коэффициентов
регрессии вычисляем по формулам (2.47) − (2.50):

24.

Для проверки значимости коэффициентов регрессии рассмотрим следующие соотношения:
Отсюда видно, что все коэффициенты регрессии значимы.
Пользуясь формулой (2.51), вычисляем оценку дисперсии
адекватности:

25.

Число степеней свободы, связанных с этой оценкой
дисперсии, находим по формуле (2.52):
адекватно представленным результатам эксперимента.
Перейдем в уравнение регрессии от кодированных переменных к физическим. Пусть в нашем
примере кодированные переменные X1 и X2 представляют собой температуру и концентрацию, причем координаты центра плана x01= 60°С и
x02= 30%, а шаги варьирования ∆x1= 5°С и ∆х2= 1%.

26.

Тогда на основании формулы (2.8) справедливы следующие выражения:
Подставляя их в полученное в этом примере уравнение
регрессии, преобразуем его к виду
Пользуясь таким уравнением, исследователь избавляется от необходимости
переводить всякий раз условия опыта в кодированные переменные.