Дробный факторный эксперимент. Метод перевала

1. Дробный Факторный Эксперимент

Метод перевала

2. Построение матрицы дробных факторных экспериментов

• Пусть необходимо найти коэффициенты полинома
• y=bo+b1x1+b2x2+b3x3
• Если использовать ПФЭ, то при наличии трех факторов
число опытов равно 23=8, но в тоже время для
определения 4-х коэффициентов достаточно выполнить
5 опытов. Чтобы сократить число опытов по сравнению
с ПФЭ используют дробный факторный эксперимент
ДФЭ.
• Матрица ДФЭ предоставляет собой основу матрицы
ПФЭ, но с меньшим числом факторов планируемого
эксперимента. Остальные факторы, не вошедшие в
основу плана, определяются в виде произведения
факторов основы плана.

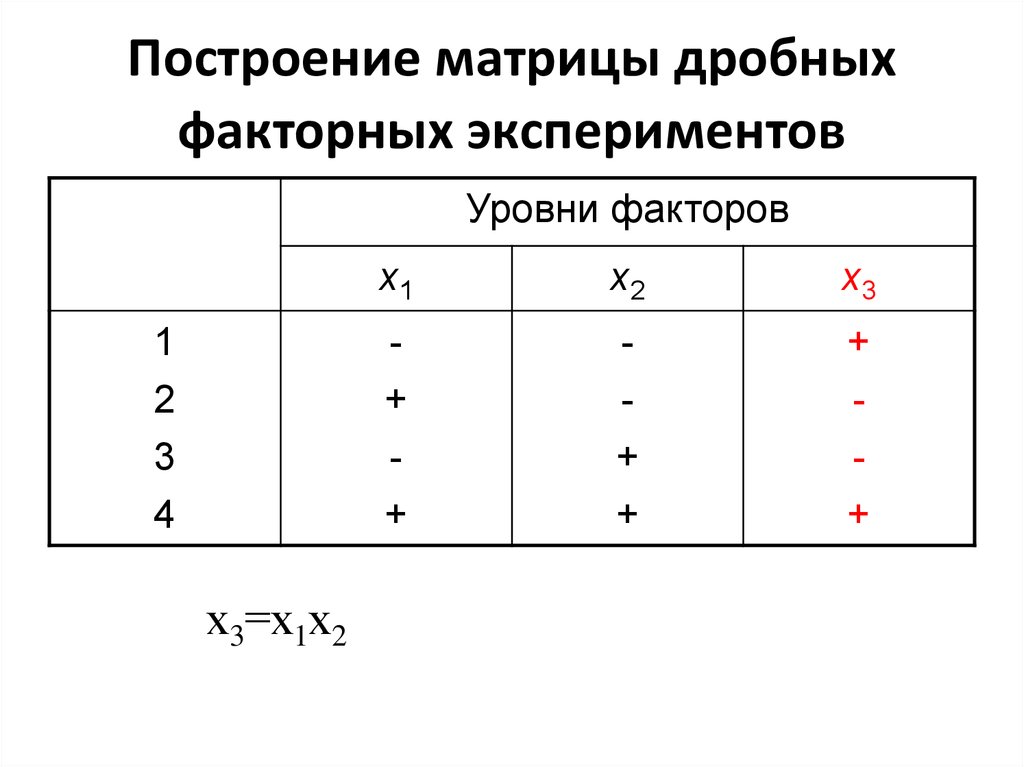
3. Построение матрицы дробных факторных экспериментов

Уровни факторов
1
2
3
4
х3=х1х2
х1
х2
х3
+
+
+
+
+
+

4. Число опытов в ДФЭ

• Произведение факторов, определяющие уровни
факторов не вошедшие в основу плана называют
генерирующим соотношением или генератором
ДФЭ.
• Матрицы позволяют дробными репликами.
• Если один фактор определяется с помощью
генератора, то число опытов сокращается в 2 раза,
если два фактора - то в 4 раза. В общем случае
число опытов сокращается в 2m раз, где m – число
факторов определяемых с помощью генераторов.
• Число опытов в ДФЭ n=2k-m, k- общее число опытов.

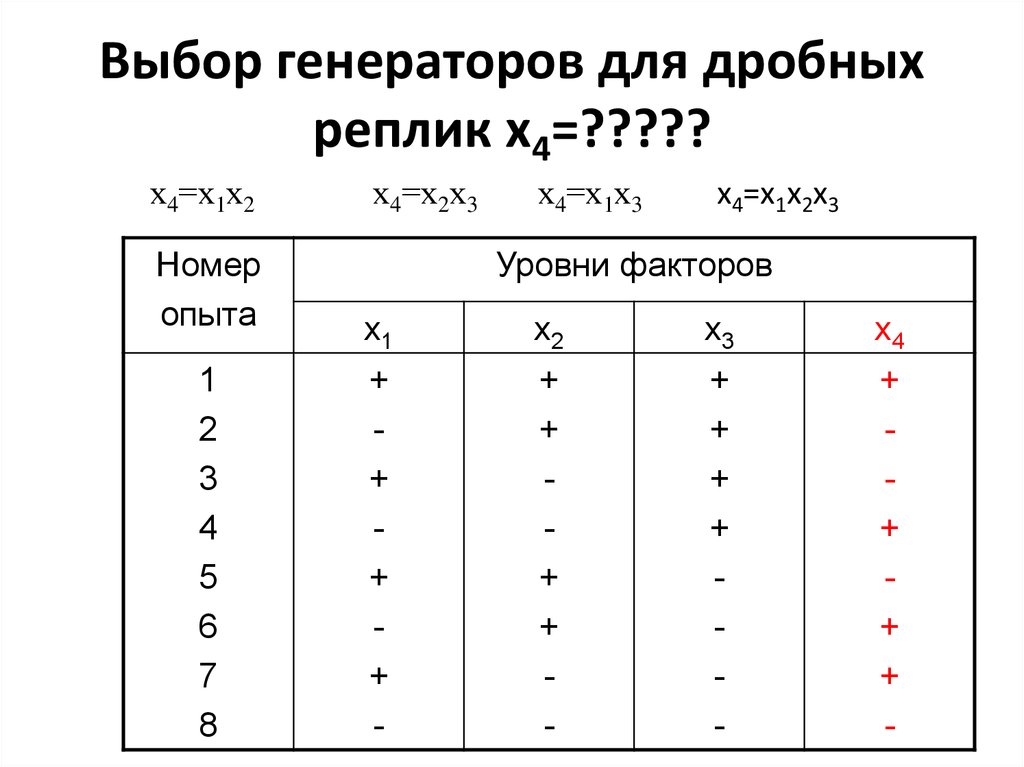
5. Выбор генераторов для дробных реплик х4=?????

х4=х1х2
Номер
опыта
1
2
3
4
5
6
7
8
х4=х2х3
х4=х1х3
х4=х1х2х3
Уровни факторов
х1
+
+
+
+
-
х2
+
+
+
+
-
х3
+
+
+
+
-
х4
+
+
+
+
-

6. Свойства ПФЭ и ДФЭ

• Симметричность относительно центра
эксперимента, т.е. алгебраическая сумма
элементов вектора столбца равна нулю.
• Условие нормировки: сумма квадратов
элементов каждого столбца равна числу
опытов.
• Ортогональность: сумма почленных
произведений любых двух векторов столбцов
матрицы равна нулю
• Ротатабельность: точки в матрице
планирования подбираются так, чтобы
точность предсказания значений параметра
оптимизации была одинакова на равных
расстояниях от центра эксперимента и не
зависела от направления.

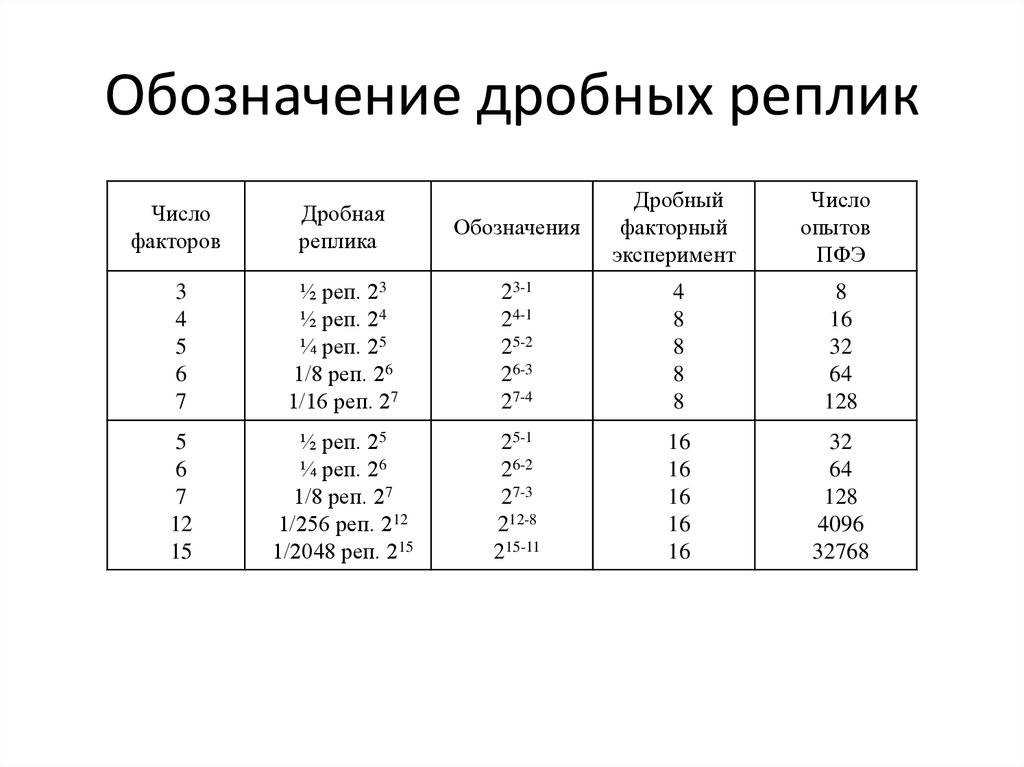
7. Обозначение дробных реплик

Обозначения
Дробный
факторный
эксперимент
Число
опытов
ПФЭ
½ реп. 23
½ реп. 24
¼ реп. 25
1/8 реп. 26
1/16 реп. 27
23-1
24-1
25-2
26-3
27-4
4
8
8
8
8
8
16
32
64
128
½ реп. 25
¼ реп. 26
1/8 реп. 27
1/256 реп. 212
1/2048 реп. 215
25-1
26-2
27-3
212-8
215-11
16
16
16
16
16
32
64
128
4096
32768
Число
факторов
Дробная
реплика
3
4
5
6
7
5
6
7
12
15

8. Принцип создания дробной реплики

• Рассмотрим модель без третьего фактора:
• Если мы считаем, что уравнение линейно, то , а вектор столбец
можно использовать для нового фактора . Однако в данном случае не
будет раздельных оценок, которые были в полном факторном
эксперименте. Оценки будут
b1 1 23
смешиваться следующим образом:
b2 2 13
b3 3 12
• В том случае, если предположение о линейности верно, то
Таким образом можно поставить четыре опыта для оценки влияния
трех факторов. Для оценки смешивания мы воспользовались
половиной полного факторного эксперимента, 23 или полу репликой.
Если бы мы приравняли
, то получили бы вторую половину
полного факторного эксперимента. b1 1 23
В этом случае:
b2 2 13
b3 3 12
• При реализации обеих полу реплик можно получать раздельные
оценки для линейных эффектов и эффектов взаимодействия.

9. ГЕНЕРИРУЮЩЕЕ СООТНОШЕНИЕ

• При построении полу реплики 23-1 х3 можно
прировнять +(х1х2) или -(х1х2) . Тогда для
произведения трех столбцов матрицы будет
выполняться следующее:
• Это - определяющий контраст или
символическое обозначение произведения
столбцов, равное ±1.
• Получаем из

10. Обобщающий определяющий контраст

• Соотношение, показывающее с каким из эффектов
смешан данный эффект называется генерирующим
соотношением.
• Эффективность реплики зависит от системы
смешивания. Реплики, у которых линейные эффекты
смешены с взаимодействиями высшего порядка,
являются более эффективными, т.к. обладают
максимальной разрешающей способностью.
• С ростом числа факторов быстро увеличивается число
реплик различной дробности. Эти реплики
характеризуются обобщающими определяющими
контрастами, которые получаются перемножением по
два, по три исходных определяющих контраста.

11. Эксперимент 24-1

• Определим систему смешения х4
• Пусть определяющий контраст
• Тогда система смешения факторов
Таким образом:
x x x x
b
x 1
1
2 3 4
2
1
1
1 234
b2 2 134
b3 3 124
b4 4 123
x2 x1 x3 x4
x3 x1 x2 x4
x4 x1 x2 x3
x1 x2 x3 x4
x1 x3 x2 x4
x1 x4 x2 x3
b12 12 34
b13 13 24
b14 14 23

12. Эксперимент 25-1

• Возможны 22 решения для выбора определяющего
контраста
• определяющий контраст.
x1 x2 x3 x4 x5
x2 x1 x3 x4 x5
x3 x1 x2 x4 x5
x4 x1 x2 x3 x5
x5 x1 x2 x3 x4
b1 1 2345
b2
b3
b4
b5
2 1345
3 1245
4 1235
5 1234

13. План 25-2 (достаточно 16 опытов)

• Пусть х4=х1х3, х5=х1х2х3, тогда определяющие контрасты будут:
1 x1 x3 x4 и 1 x1 x2 x3 x5 Перемножив получим 1 x2 x4 x5
• Чтобы полностью охарактеризовать разрешающую способность
реплики, необходимо записать обобщающий определяющий
контраст:
• Система смешивания определяется умножением обобщающего
определяющего контраста на и т.д.
x1 x3 x4 x1 x2 x4 x5 x2 x3 x5
x2 x1 x2 x3 x4 x4 x5 x1 x3 x5
x3 x1 x4 x2 x3 x4 x5 x1 x2 x5
x4 x1 x3 x2 x5 x1 x2 x3 x4 x5
x5 x1 x3 x4 x5 x2 x4 x1 x2 x3
• Если получилось, что
b1 1 34 1245 235
b2 2 1234 45 135
b3 3 14 2345 125
b4 4 13 25 12345
b5 5 1345 24 123

14. Метод перевала

• Если возникают сомнения: можно ли пренебрегать парными
взаимодействиями, тогда следует поставить вторую серию опытов и
выбрать другую ¼ реплики.
• При этом можно воспользоваться методом перевала. Смысл этого
метода заключается в том, что вторая четверть реплики получается из
первой путем изменения всех знаков матрицы на обратные.
1). x4 x1 x3
x5 x1 x2 x3
1 x1 x3 x4 x1 x2 x3 x5 x2 x4 x5
x1 x3 x4 x2 x3 x5 x1 x2 x4 x5
b1 1 34 235 1245
b1 1 235
x2 x1 x2 x3 x4 x1 x3 x5 x4 x5
b2 2 123 135 45
b2 2 135 ,
2).
x4 x1 x3
x5 x1 x2 x3
1 x1 x3 x4 x1 x2 x3 x5 x2 x4 x5
x1 x3 x4 x2 x3 x5 x1 x2 x4 x5
x2 x1 x2 x3 x4 x1 x3 x5 x4 x5
x3 x1 x4 x1 x2 x5 x2 x3 x4 x5
b1 1 34 235 1245
b1 1 34
b2 2 1234
b3 3 14
b4 4 13
b5 5 1345