Математическое моделирование процессов в природных, социально-экономических средах

1. Курс «Математическое моделирование процессов в природных, социально-экономических средах»

КУРС
«МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ПРОЦЕССОВ В ПРИРОДНЫХ,
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ СРЕДАХ»

2. Глава 2 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ

ГЛАВА 2
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Часть 1
2

3.

1.
Функциональные пространства
Пусть x(t), y(t), z(t), …, u(t), … функции, заданные на отрезке
[a,
b]
и
обладающие
некоторыми
оговоренными
заранее
свойствами – непрерывностью, дифференцируемостью и т. д. Их
сумма, разность и произведение на число определены на этом же
отрезке и обладают теми же свойствами. В этом случае будем
говорить,
что
определенно
функциональное
пространство,
элементами (точками, векторами) которого являются функции.
3

4.

Если дополнительно для любой пары x(t), y(t) функций
определено число x y , называемое расстоянием (нормой) и
обладающее свойствами обычного расстояния, т. е.
1.
x 0 x 0,
x 0 x ( t ) 0,
2.
ax a x , а - скаляр
3.
x y x y,
(аксиома треугольника для норм)
то функциональное пространство называется нормированным.
4

5.

Наличие в функциональном пространстве расстояния позволяет
обычным образом определить окрестность элементов этого
пространства -окрестностью элемента х0 является множество
элементов х этого пространства, таких, что
x x0 .
Как и в обычном анализе, можно определить сходимость
последовательности элементов, т. е. ввести понятие предела
x lim xn 0 n0 : n n0
n
x x0 .
5

6.

Заметим, что на одном и том же множестве функций расстояние
можно
задавать
по-разному.
При
этом
будут
получаться
различные нормированные пространства. Близость элементов в
них будет пониматься по-разному и, соответственно, по-разному
будет выглядеть предел последовательности элементов.
Важными являются следующие два примера.
6

7.

Пример.
Рассмотрим
на
отрезке
[a,
b]
совокупность
непрерывно
дифференцируемых функций. Определим расстояние между
функциями x(t) и y(t) соотношением
x y max x ( t ) y( t ) .
(1)
t [a ,b ]
Легко
проверить,
что
свойства
1 3
для
таким
образом
определенного расстояния выполняются. Близкими в смысле
расстояния (1) будут функции, модуль разности которых невелик.
К примеру, функции x(t) = 1 + sin Mt и y(t) = 1 близки в
указанном смысле при достаточно малом и любом М, так как
x ( t ) y( t ) sin Mt max sin Mt .
t [a ,b ]
7

8.

Пример 2.
Определим
на
этом
же
множестве
(непрерывно
дифференцируемых функций) другое расстояние
x y max { x ( t ) y( t ) , x ( t ) y ( t ) }.
t [a ,b ]
(2)
Как и выше, легко проверить, что требования 1 3 выполнены.
Близкими в смысле расстояния (2) будут функции, которые
близки на отрезке [a, b] вместе со своими производными.
Функции, рассмотренные выше, при фиксированном значении
могут быть сделаны сколь угодно далекими за счет выбора M, так
как
x ( t ) y( t ) sin Mt max { sin Mt , M cos Mt } M
t [a ,b ]
при М 1.
8

9.

Заметим, что расстояние (2) «сильнее» расстояния (1) из
близости в смысле расстояния (2) следует близость в смысле
расстояния (1). Обратное, как свидетельствует рассмотренный
пример, неверно.
Выбор способа вычисления расстояния на том или ином
множестве функций, как правило, определяется содержанием
задачи, приводящим к рассмотрению именно этого класса
функций.
9

10.

Множество непрерывных функций с расстоянием (1) обычно
обозначается
С[а,b].
Множество
гладких
(непрерывно
дифференцируемых) функций с расстоянием (2) обозначается
C[1a ,b] .
10

11.

2. Основные понятия
Пусть М – некоторое множество функций.
Функционал J = J(y) – переменная величина, зависящая от
функции у(х), если каждой функции у(х) М по некоторому
правилу поставлено в соответствие число.
Вариационное
исчисление
изучает
методы,
позволяющие
находить максимальные и минимальные значения функционалов.
Рассмотрим
исчисления.
общую
постановку
задачи
вариационного
11

12.

Пусть
Rn
действительное
число
n-мерного
Евклидова
пространства, X =(х1, х2, ..., хп) вектор этого пространства; F
некоторая совокупность функций, зависящих от п переменных; Н
отображение:
H: F f (х1, х2, ..., хп) H(f(х1), f(х2), ..., f(хп)) R
Требуется найти функцию f = f(х1, х2, ..., хп) F, на которой
отображение достигает либо минимальное, либо максимальное
значение:
max(min) H(f) = H(f0),
f F.
12

13.

Например,
рассмотрим
двумерную
плоскость.
В
качестве
функции F возьмем совокупность всех непрерывных функций,
для которых сходится двойной интеграл
f ( x1 , x2 )dx1dx2 .
Отображение Н определится равенством
H( f )
f ( x1 , x2 )dx1dx2 .
13

14.

Определение 1.
Функционалом называется отображение (оператор) Н, которое
ставит каждой функции из некоторой совокупности F в
соответствие действительное число.
14

15.

Пусть F множество непрерывно дифференцируемых функций
на отрезке [0, а], а> 0, удовлетворяющих условиям:
у(х)> 0, y(0) = 0.
Функционалом будет
a
1 ( y x )2
1
H ( y)
dx
2g
y
0
Рассмотрим интеграл
1
I y 2 ( x )dx .
(1)
0
15

16.

Подставляя вместо y(x) разные функции от х, каждый раз из
равенства (1) будем получать конкретное числовое значение.
Так при у = х2
1
1
I x 4dx .
5
0
При у = х3
I
1
7
и т. д.
Если функциям поставлены в соответствие числа, то говорят, что
задан функционал.
16

17.

Многие законы природы сводятся к утверждению, что некоторый функционал в рассматриваемом процессе должен достигать
минимума или максимума. В такой формулировке эти законы
носят название вариационных принципов механики или физики.
К числу таких вариационных принципов или простейших
следствий из них принадлежат: принцип наименьшего действия,
закон сохранения энергии, закон сохранения импульса, закон
сохранения количества движения, закон сохранения момента
количества движения, различные вариационные принципы
классической и релятивистской теории поля, принцип Ферма в
оптике.
17

18.

3. Примеры вариационных задач
Пример 1.
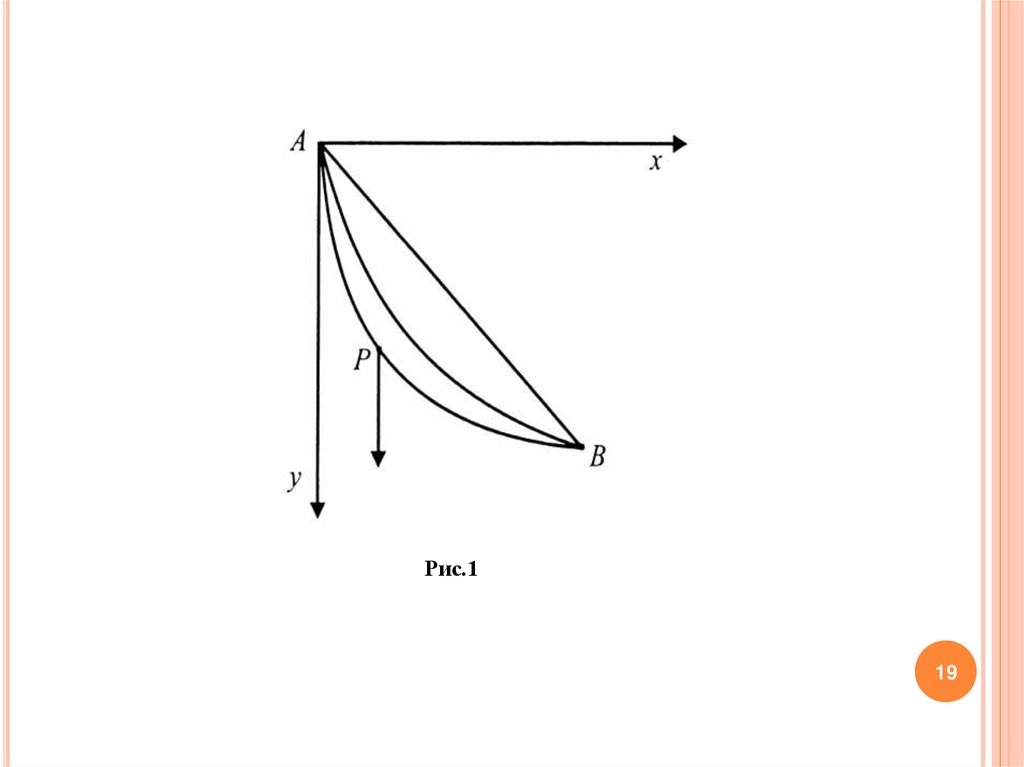
Задача о брахистохроне (Бернулли И., 1696 г.).
Среди всех кривых, соединяющих две разные точки плоскости,
найти ту, двигаясь по которой под действием силы тяжести,
материальная точка попадет из начальной точки в конечную за
кратчайшее время (трение и сопротивление среды отсутствуют)
18

19.

Рис.1
19

20.

Решение
Пусть на кривой заданы две точки А и В (рис. 1).
Из точки А в точку В под действием силы тяжести скатывается
материальная точка. Требуется найти такую кривую, чтобы
время скатывания материальной точки было минимальным. В
этом случае траектория точки называется брахистохроной.
Ось Ох направим горизонтально, ось Оу – вертикально вниз.
20

21.

Время скатывания материальной точки будет равно:
B
T dt .
(1)
A
Элемент dt можно найти из условия:
dS = vdt ,
т.е.
dS
dt
.
v
(2)
Скорость скатывающейся материальной точки равна:
v 2gy .
(3)
Элемент dS, как дифференциал дуги кривой, равен:
2
2
dS dx dy .
(4)
21

22.

Причем,
dy y x dx .
Учитывая равенства (2) (4), имеем:
1 ( y x )2 dx
1 ( y x )2
dt
dx .
2 gy
2 gy
Согласно равенству (4) получаем:
x2
T
x1
1 ( y x )2
dx .
2 gy
(5)
Следовательно, чтобы найти минимальное время перемещения,
нужно минимизировать интеграл (5).
22

23.

Замечание 1.
Брахистохроной
не
будет
отрезок
вертикальной
прямой,
соединяющий А и В, хотя он и является кратчайшим расстоянием
между этими точками, так как при движении по прямой скорость
движения будет нарастать сравнительно медленно. Если же мы
возьмем кривую, более круто спускающуюся около точки А вниз,
то хотя путь и удлинится, но значительная часть пути будет
пройдена с большей скоростью. Брахистохрона – дуга циклоиды.
23

24.

Замечание 2.
Предположим, что начальная скорость точки равна нулю и
скатывание осуществляется без трения. Тогда ее скорость v на
высоте у полностью определяется высотой, с которой точка
начала свое движение: кинетическая энергия точки должна быть
равна изменению потенциальной при спуске на уровень у
mv 2
mgy v 2 gy .
2
24

25.

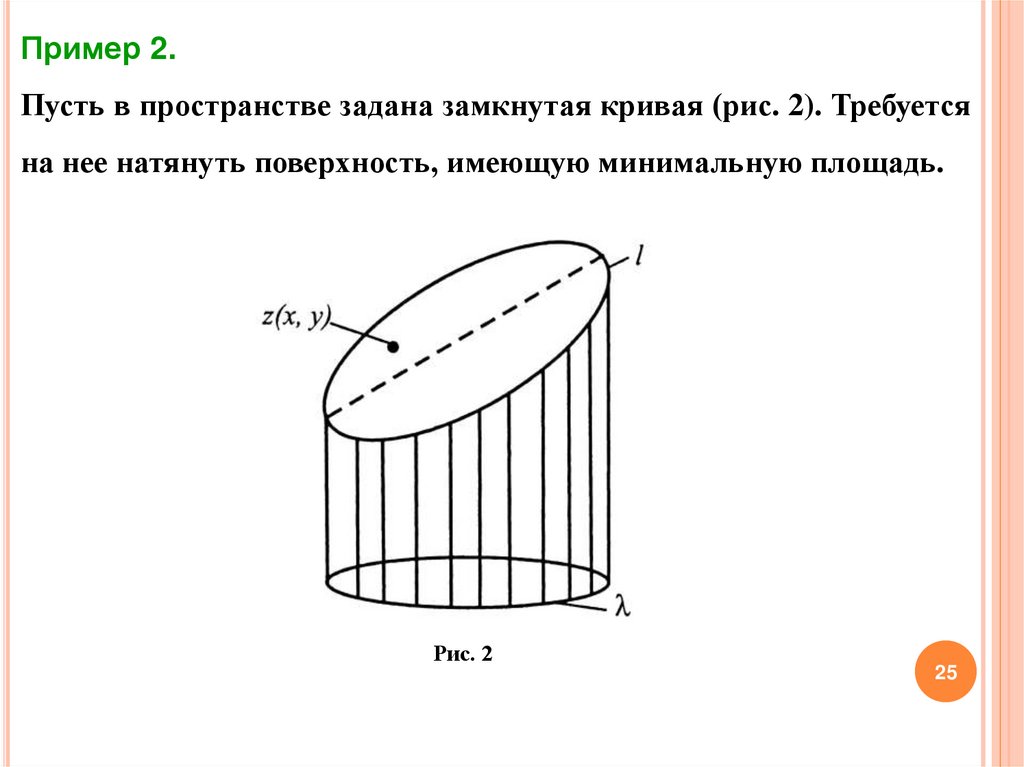
Пример 2.
Пусть в пространстве задана замкнутая кривая (рис. 2). Требуется
на нее натянуть поверхность, имеющую минимальную площадь.
Рис. 2
25

26.

Решение
Уравнение поверхности можно записать в виде:
z=z(x,y).
Пусть проекция линии l на плоскость будет плоской кривой , а
область, ограниченная кривой , D. Тогда площадь искомой
поверхности будет выражаться интегралом
S 1 ( z x )2 ( z y )2 dxdy .
(6).
( D)
Тем самым задача сводится к минимизации интеграла (6).
26

27.

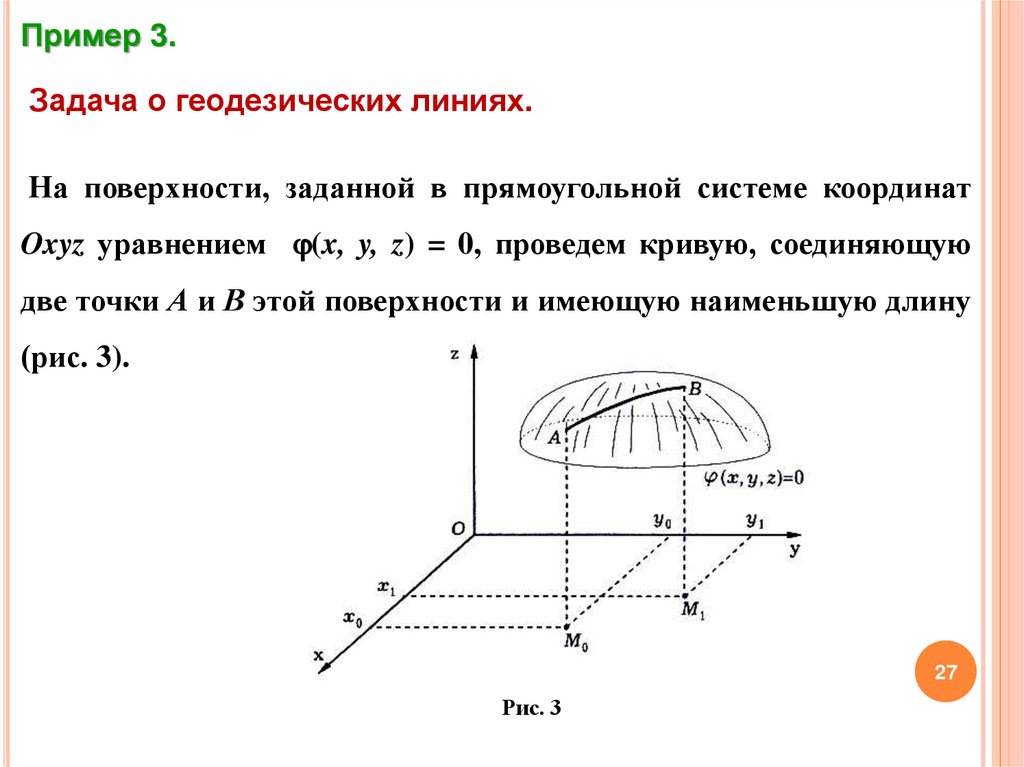
Пример 3.
Задача о геодезических линиях.
На поверхности, заданной в прямоугольной системе координат
Oxyz уравнением (x, y, z) = 0, проведем кривую, соединяющую
две точки А и В этой поверхности и имеющую наименьшую длину
(рис. 3).
27
Рис. 3

28.

Наименьшие по длине линии между двумя точками некоторой
поверхности являются геодезическими линиями этой поверхности.
Например,
геодезическими
линиями
плоскости
являются
прямые, геодезическими линиями на сфере дуги большого круга
Предположим, что поверхность (x, y, z) =0 является гладкой, а
искомая кривая может быть задана уравнениями у = у(х), z = z(х),
х [а, b], с помощью гладких функций у(х) и z(х). Тогда ее длина L
равна:
B
L
A
b
dx 2 dy 2 dz 2
1 ( y ) 2 ( z ) 2 dx .
(7).
a
28

29.

Задача свелась к определению таких гладких на отрезке [а, b]
функций у = у(х) и z = z(х), что
(х, у(х), z(x)) 0, у(х0) = y0, у(х1) = y1, z(x0) = z0, z(x1) = z1,
а интеграл (7) принимает минимальное значение.
29

30.

4. Вариационные задачи
Основная задача вариационного исчисления представляет собой
частный случай экстремальных задач в функциональных
пространствах
I(Y) min, Y Y ,
где Y некоторое множество функций.
Специфика ее заключается в выборе множества функций Y и
выборе конкретного функционала I.
30

31.

Основная
задача
является
обобщением
задач
нелинейного
программирования. В этом случае планам задач нелинейного
программирования соответствуют допустимые кривые задач
вариационного исчисления.
Известны
три
способа
перехода
от
задач
вариационного
исчисления к задачам нелинейного программирования.
31

32.

Первый
с п о со б
прототипа
основан на дискретизации физического
вариационной
задачи.
Например,
вместо
вариационной задачи (п.3) получится задача нелинейного
программирования,
если
материальную
точку
заставить
двигаться из А в В по цепи с конечным числом звеньев
(см. рис. 1).
В т о р о й с п о со б заключается в разностной аппроксимации
модели
вариационной
задачи,
при
которой
непрерывные
функции заменяются на сеточные, производные на разностные
отношения, интегралы на интегральные суммы.
Тр е т и й с п о со б состоит из разностной аппроксимации условий
оптимальности вариационной задачи.
32

33.

Приведем несколько примеров других вариационных задач.
1. Задача с нефиксированным отрезком [а, b], отличающаяся тем,
что числа а и b (оба или одно) не задаются, а выбираются из
условия минимума функционала.
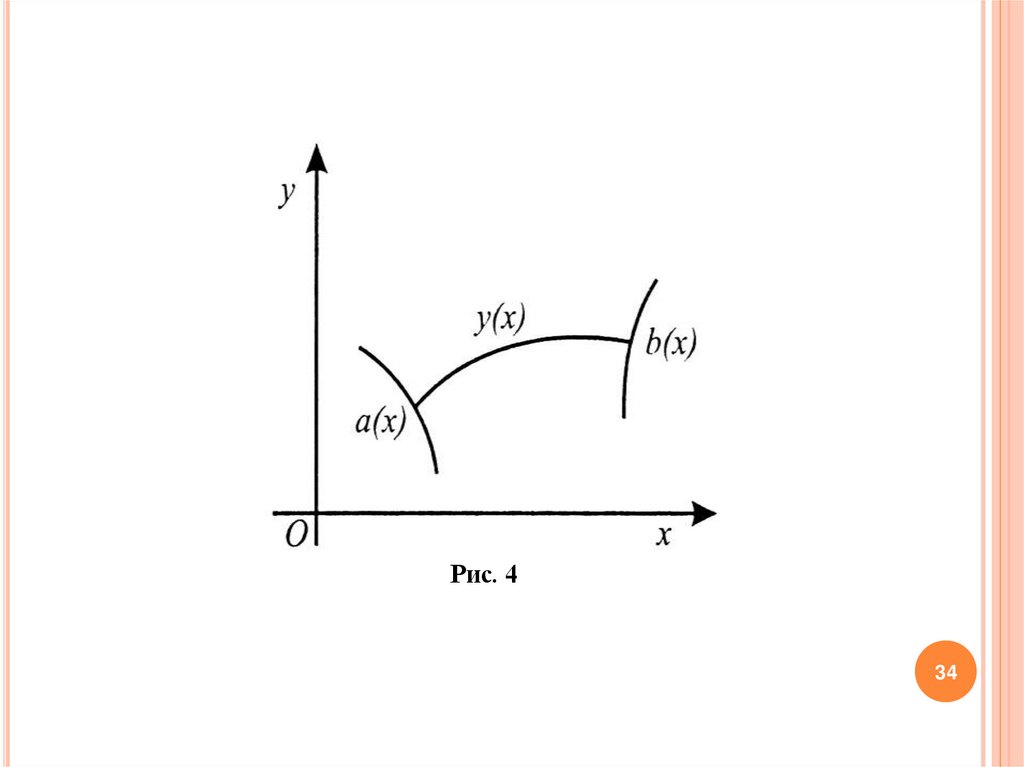
2. Задача с подвижными концами. В ней один конец кривой у(х)
должен лежать на заданной линии а(х), а другой - на линии b(х)
(рис. 4).
33

34.

Рис. 4
34

35.

Спасибо за внимание!
35