Similar presentations:
Анализ некоторых видов движения. Уравнение движения
1.
Анализ некоторых видов движенияУравнение движения
at 2
r t r0 Vt
2
Где r0- радиус-вектор, проведенный из начала
координат в рассматриваемую точку, V- скорость,
а- ускорение, t- время
Различают, равномерное и равнопеременное
движение. Для простоты рассмотрим только
прямолинейное движение
2.
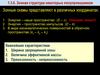
- равномерное движениеV t const; a t 0
20
15
S, m
r t r0 Vt
10
5
S t Vt
0
0
1
2
3
4
5
6
7
6
7
8
9
t, c
0,5
2,5
0,3
a, m/c 2
V, m/c
2
1,5
1
0,5
0,1
-0,1 0
1
2
3
4
5
-0,3
0
0
1
2
3
4
5
t, c
6
7
8
9
-0,5
t, c
8
9
3.
-неравномерное движениеV2
V t const;a n
0
R
Если a const , то движение называют
равнопеременным (ускоренным или замедленным)
4.
• Равноускоренное движение2
at
S t Vt
2
120
S, m
100
80
60
40
20
0
0
1
2
3
4
5
6
7
8
9
t, c
12
1,2
1
8
a, m/c 2
V, m/c
10
6
4
2
0,8
0,6
0,4
0,2
0
0
1
2
3
4
5
t, c
6
7
8
9
0
0
1
2
3
4
5
t, c
6
7
8
9
5.
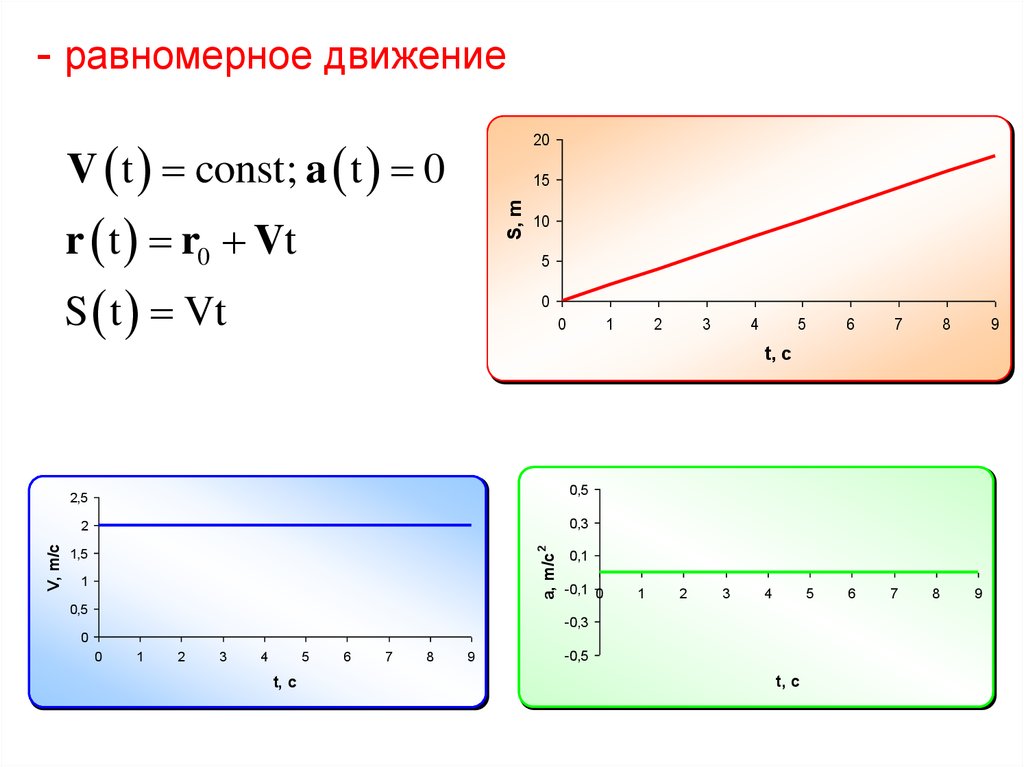
2at
S t Vt
2
• Равнозамедленное движение
60
S, m
50
40
30
20
10
0
0
1
2
3
4
5
6
7
8
9
16
14
12
10
8
6
4
2
0
0
-0,2
a, m/c 2
V, m/c
t, c
0
1
2
3
4
5
-0,4
-0,6
-0,8
-1
0
1
2
3
4
5
t, c
6
7
8
9
-1,2
t, c
6
7
8
9
6.
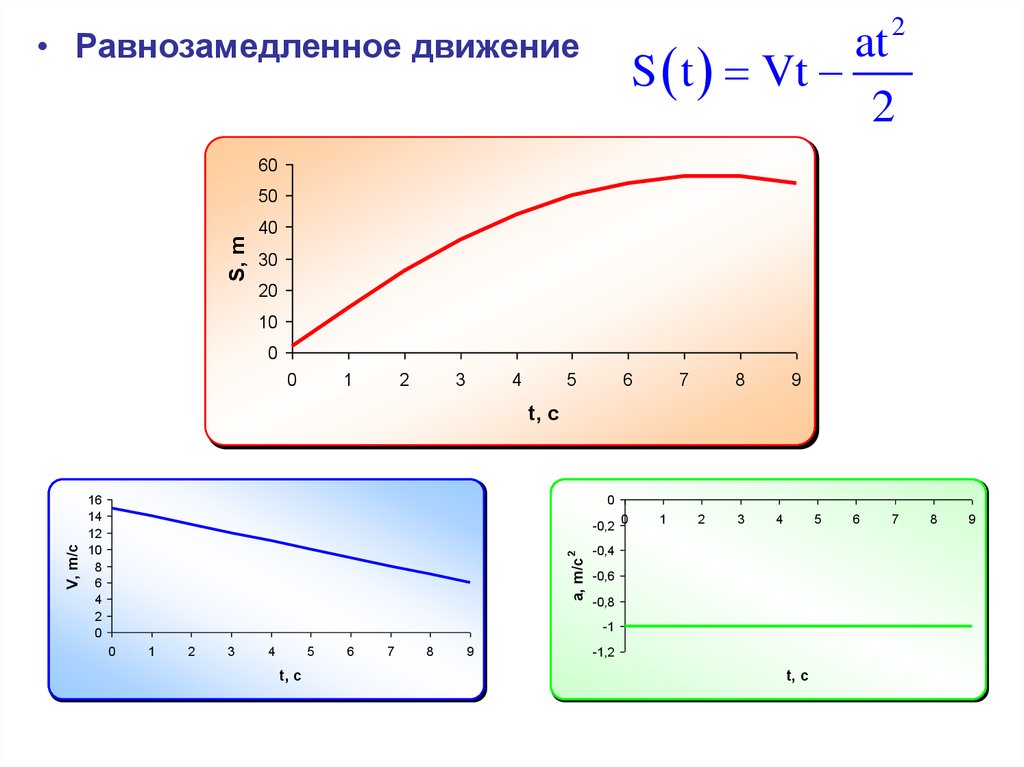
Момент инерцииМомент инерции материальной точки
относительно оси вращения равен
произведению массы точки на квадрат
расстояния от нее до оси вращения
J = mR
2
Момент инерции точки
Зависит только от ее
кратчайшего
расстояния до оси
вращения.
C
.
R
r
O
m
7.
Для системы материальных точек момент инерции равен суммемоментов инерции отдельных точек
2
i
i i
i
i
Если масса распределена непрерывно с плотностью (r ) , то тело
можно разбить на малые объемы ΔV с массами Δmi = ρi ΔVi .
i
Эти объемы можно рассматривать как материальные точки. Суммируя
их моменты инерции, получим момент инерции всего тела
J = J = m R
J = Δmi Ri2 = ρi ΔVi Ri2
В пределе
ΔVi 0
i
i
сумма переходит в интеграл по объему тела
J = R dm = R ρdV
2
2
(4.1.2)
Момент инерции твердого тела зависит от распределения в
нем массы, расстояния и ориентации оси относительно тела.
8.
В качестве примера найдем момент инерцииоднородного диска относительно оси,
перпендикулярной к его плоскости и проходящей
через его центр.
Пусть D - толщина диска, R0 – его радиус. Поскольку
диск однородный ( ρ = const ), то
J = R ρdV = ρ R dV
2
2
Разобьем диск на тонкие
кольцевые слои толщиной dR
и радиусами R.
Объем каждого слоя равен
dV = D 2πRdR
9.
Момент инерции диска равен сумме моментовинерции всех кольцевых слоев, поэтому он равен
интегралу
R0
π
4
J = D 2π ρ R dR = D ρ R0
2
0
3
Выражая массу диска через плотность
2
0
m = πR D ρ
получаем момент инерции однородного диска
или цилиндра
1
2
J = m R0
2
10.
Закон всемирного тяготенияДавно замечено, что звезды на небосводе
сохраняют взаимное расположение, тогда как
планеты описывают сложные, петлеобразные
траектории. Для объяснения такого поведения
небесных тел использовались два представления.
Первой планетарной моделью была
геоцентрическая система Птоломея (II век до н.э.),
который считал, что центром Вселенной является
Земля, а движение планет происходит по малым
кругам, центры которых в свою очередь движутся
по большим кругам вокруг Земли.
11.
Кеплер сформулировал 3 закона :1) каждая планета движется по эллипсу, в одном из
фокусов которого находится Солнце
2) радиус-вектор планеты за равные промежутки
времени описывает одинаковые площади
3) квадраты периодов обращения планет вокруг
Солнца относятся как кубы больших полуосей их
орбит
12.
В 1678 году Ньютон на основе законов механики изаконов Кеплера открыл закон всемирного
тяготения :
между любыми двумя материальными точками
с массами m1 и m2 действует сила взаимного
притяжения, пропорциональная произведению
масс и обратно пропорциональная квадрату
расстояния между ними
m1m2
F =G 2
r
где G = 6.672·10-11 Н м2/кг гравитационная
постоянная.
13.
Малое значение постоянной G показывает, чтосила гравитационного взаимодействия заметна
только для очень больших масс. Поэтому
гравитационное взаимодействие не играет
существенной роли в механике атомов и молекул.
Однако движение больших тел, таких как Луна,
планеты, спутники полностью определяется
гравитационными силами.
Как и электрические силы, гравитационные
силы обратно пропорциональны квадрату
расстояния между телами. Но в отличие от
электрических сил, которые могут быть как силами
притяжения, так и силами отталкивания,
гравитационные силы являются только силами
притяжения.
14.
Однако, еще Ньютон отметил, что за счетвзаимного притяжения планеты никогда не
движутся точно по эллипсам и не обращаются
дважды по одной и той же орбите.
По отклонениям орбиты Урана астроном
Леверье в 19 веке теоретически предсказал новую
планету – Нептун, которую обнаружили в
указанной им области неба. В 1930 году по
возмущениям орбиты Нептуна был открыт Плутон.
В 2006 году астрономический конгресс принял
решение исключить Плутон из числа планет,
поскольку его размеры и масса сравнительно
невелики и таких тел как он в солнечной системе
много.
15.
Гравитационное взаимодействиеосуществляется посредством гравитационного
поля, которое является одной из форм
существования материи.
Любое тело создает гравитационное поле в
окружающем его пространстве и изменяет
свойства пространства.
Это поле проявляет себя через силу,
действующую на другие тела. Данная сила не
зависит от того являются ли тела заряженными
или нейтральными и определяется только
массами тел.
16.
В поле тяготения Земли величина напряженностигравитационного поля
равна ускорению
свободного падения, среднее значение которого
на поверхности Земли равно 9.81 м/c2.
Зная радиус Земли RЗ = 6.38 106 м и
гравитационную постоянную, Кавендиш впервые
определил массу Земли
2
gRЗ
MЗ =
5.98 10 24 кг
G
17.
С удалением от Земли сила тяготения Землиуменьшается. Вместе с ней уменьшается и
напряженность ее гравитационного поля, то есть
ускорение свободного падения
MЗ
g =G
2
(RЗ + h)
где h - высота тела над поверхностью Земли.
Поэтому в горах ускорение свободного падения
меньше, чем на уровне моря.
18.
Необходимо также учитывать, что за счет силыКориолиса Земля сплюснута на полюсах – ее
радиус на экваторе на 21 км больше радиуса на
полюсе:
Rз(экватор) = 6378 км, Rз(полюс) = 6357 км.
За счет этого ускорение свободного падения
на экваторе меньше, чем на полюсах
на 0.00006 м/c2.
19.
Кроме того, на величину и направлениеускорения свободного падения влияет
центробежная сила инерции
, связанная с
вращением Земли вокруг своей оси.
Эта сила направлена в сторону,
противоположную силе притяжения, и поэтому
уменьшает ускорение свободного падения.
Сила инерции равна нулю на полюсах.
На экваторе сила инерции максимальна и
приводит к уменьшению ускорения свободного
падения на величину
2
2π
2
aз =
Rз 0.034 м/с
Tз
20.
В результате влияния всех факторовускорение свободного падения меняется с
широтой от 9.78 м/c2 на экваторе до 9.83 м/c2 на
полюсах. На средних широтах ~ 45º ускорение
близко к значению g = 9.81 м/c2.
Вес тела на экваторе примерно на 0.5%
меньше веса того же тела на полюсе.
21.
Две гири массами m1= 2 кг и m2=1 кг соединены нитью,перекинутой через блок массой m=1 кг. Найти ускорение
а, с которым движутся гири, и силы натяжения Т1 и Т2
нитей, к которым подвешены гири. Блок считать
однородным диском. Трением пренебречь.
Запишем в векторной форме
уравнения поступательного
движения первой и второй
гири:
m1a=m1g+T1; m2a=T2+m2g
и уравнение вращательного
движения диска Jε=M1+M2,
где M1- момент силы
натяжения нити T1, M2- момент
силы натяжения нити T2.
22.
Спроецируем первые 2 уравнения на ось х, апоследнее на ось y. Получим систему 4 уравнений:
1
m 2 a m 2 g T1 2
J RT1 RT2 3
a R 4
m1a m1g T1
Подставим (4) в (3)
a
J R T1 T2
R
5
Вычтем (2) из (1), подставим в полученное выражение
(5) и найдем а:
a
m1 m 2 g
m1 m 2 m 2
2.8 m c 2
6
23.
Подставляя (6) в (1) и (2), получимT1 m1 g a 14 H
T2 m 2 g a 12.6 H




















 physics
physics