Свойства степени с натуральным показателем

1.

«Свойства степени с натуральным показателем»

2. Тема урока: Свойства степени с натуральным показателем

Эпиграф урока
«Пусть кто-нибудь попробует вычеркнуть
из математики степени,
и он увидит, что без них далеко не уедешь»
М.В. Ломоносов

3. Определяем цель урока:

повторить, обобщить и
систематизировать знания по теме;
проверить усвоение знаний и умений
применять свойства степени при
решении упражнений

4. ТЕОРЕТИЧЕСКАЯ РАЗМИНКА

Степень- это произведение одинаковых
множителей.
Выражение аn называют степенью
а–
основание степени
n – показатель степени

5. Вспомним правила !

Если показатель четное число,
то значение степени всегда
положительное.
Если показатель нечетное число,
то значение степени всегда
отрицательное.

6. Вычислите устно

72
1
1
8
23
2
15
(-4)2
07
-42
33- 52
102 + 82
1
3
2
(10 - 7)3

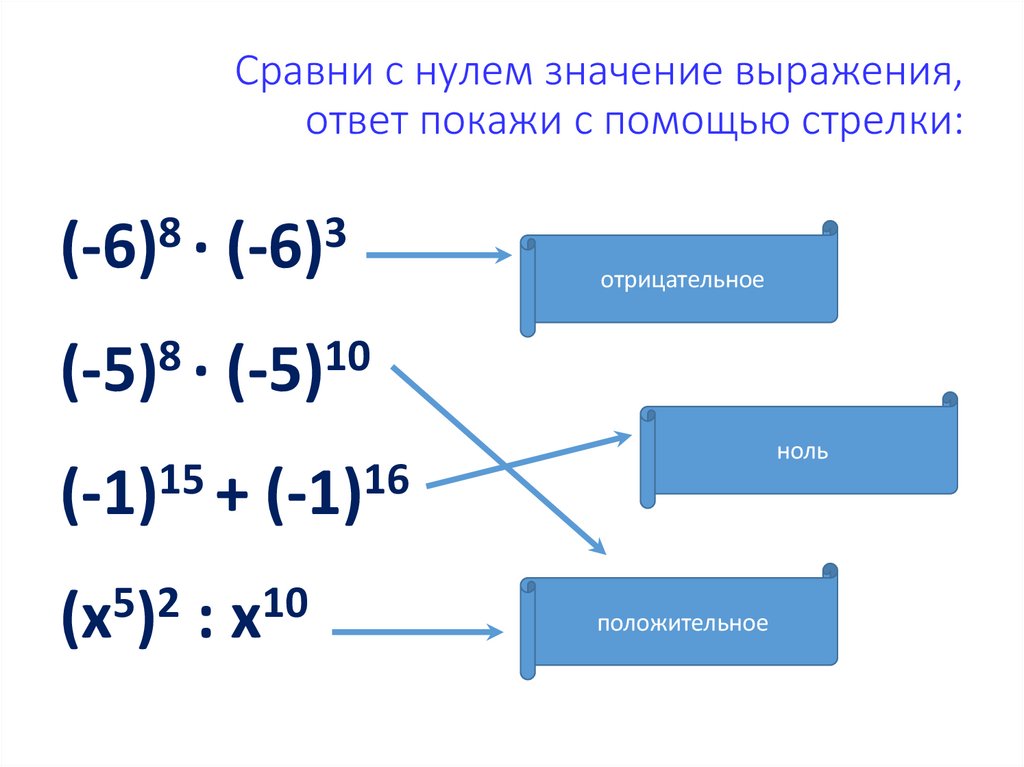
7. Сравни с нулем значение выражения, ответ покажи с помощью стрелки:

8
3
(-6) ∙ (-6)
отрицательное
(-5)8 ∙ (-5)10
ноль
15
16
(-1) + (-1)
(х5)2 : х10
положительное

8.

Найди значения выражений сам
Вариант 1.
Вариант 2.
а ) 5 32
= -45
а) 4 2 2
= -16
б )( 5 3) 2
= 225
б )( 4 2) 2
= 64
в )5 ( 3) 2
= 45
в )4 ( 2) 2
= 16
г ) 52 ( 3) 2 = -225
г ) 4 2 ( 2) 2 = -64
Проверь себя сам

9.

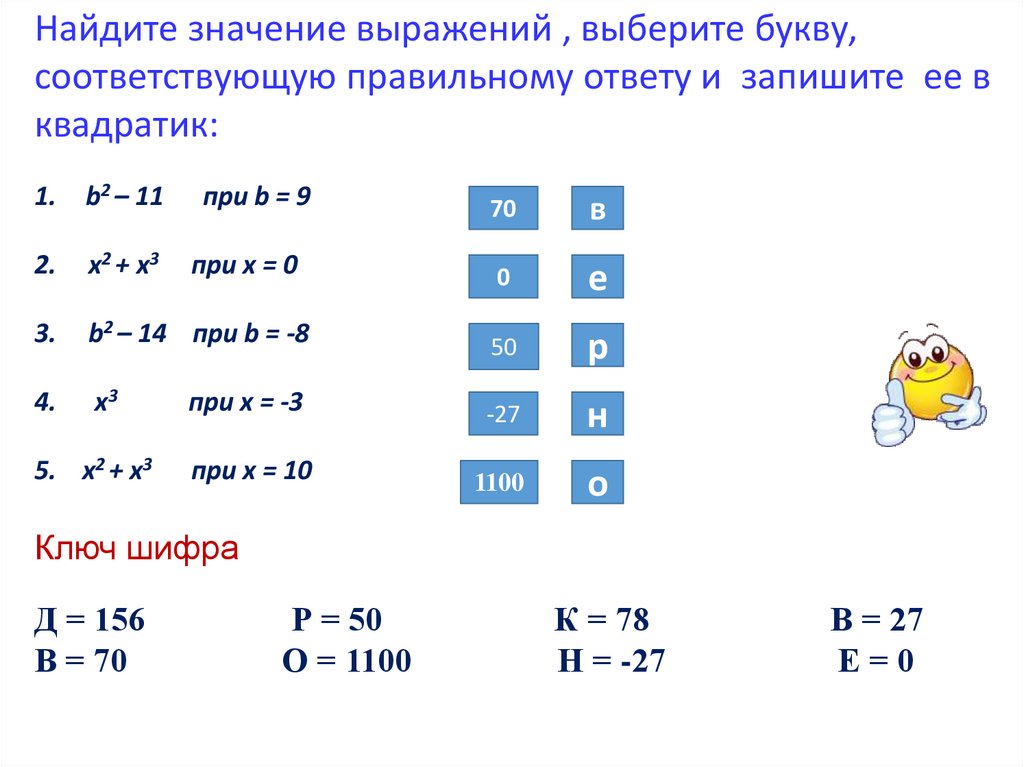
Найдите значение выражений , выберите букву,
соответствующую правильному ответу и запишите ее в
квадратик:
1.
b2 – 11
при b = 9
70
в
2.
х 2 + х3
при х = 0
0
е
3.
b2 – 14 при b = -8
50
р
4.
х3
при х = -3
-27
н
5. х2 + х3
при х = 10
1100
о
Ключ шифра
Д = 156
В = 70
Р = 50
О = 1100
К = 78
Н = -27
В = 27
Е=0

10.

Вспомним свойства степени!
1. Произведение степеней :
При умножении степеней с одинаковым
основанием надо:
основание оставить прежним,
а показатели степеней сложить.
n
k
n+k
a ·a =a

11.

2. Частное степеней :
При делении степеней с
одинаковым основанием надо:
основание оставить прежним,
а показатели вычесть.
an : ak=an - k

12.

3. Возведение степени в степень
При возведении степени в степень надо:
основание оставить прежним,
а показатели степеней перемножить.
n
к
nk
(a ) = a

13. 4. Возведение в степень произведения

возвести в эту степень каждый
множитель
ab a b
n
n
n

14. Представьте выражение в виде степени.

5
7
х ∙х
3
5
(a )
2
5∙5
2
3
(3х )
3
ссс
1
а
8
2
а :а
0
а
6
2
(-b) : (-b)
0
0

15.

Вариант 1.
79 75
1) Вычислить 12
7
а ) 49 б ) 7 в )14
2) Упростить (а 4 ) 6 : (а 3 ) 3
а) а
б ) а12 в )а15
3) При каком х выполняется равенство
56 5 х 510
а )125 б )25
в )4
4) При каком х выполняется равенство
56 5 х 510
а)125 б )25
в )4

16. Повторим правила!

Одночлен – это выражение, состоящее из произведения
чисел, переменных и их степеней.
Одночлен, в котором единственный числовой
множитель стоит на первом месте и степень любой
переменной повторяется только один раз называется
одночленом стандартного вида
Числовой множитель одночлена стандартного вида
называется коэффициентом одночлена.
Сумма показателей всех степеней переменных
называется степенью одночлена.

17. Приведите одночлены из левого столбика к стандартному виду, выберите буквы, соответствующие верным ответам

1) 2ху∙3х2у5
2) 3ху3∙ х3у6
3) -0,6ас3 ∙(-8)а2с4
4) 0,5 x2у ∙(-6ху)
5) -5а2с∙2ас∙(-0,6с3)
С
3х4 у9
Я
3ху3
Ю
6a3 с5
О
-3х3у2
Ж -8а2 с4
Б
6х3у6
В
0,6ас5
Г
4x2у5
З
4,8а3с7

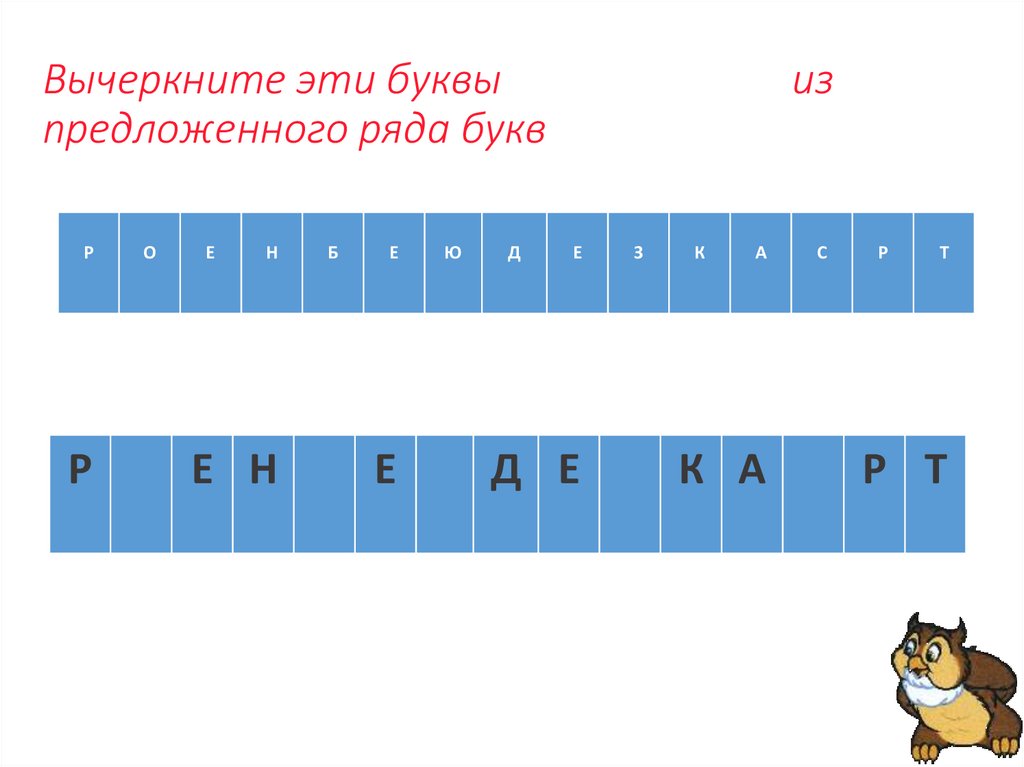
18. Вычеркните эти буквы из предложенного ряда букв

Вычеркните эти буквы
предложенного ряда букв
Р
Р
О
Е
Н
Е Н
Б
Е
Е
Ю
Д
из
Е
Д Е
З
К
А
К А
С
Р
Т
Р Т

19.

Рене Декарт
(1596 - 1650)
французский
математик,
который первый
ввел понятие
степени числа