Similar presentations:
Нормальное распределение
1. Нормальное распределение.
Непрерывная случайная величина, плотность вероятностикоторой выражается следующей формулой,
1
f (x)
2
( x a ) 2
2
2
e
;
( 0)
называется распределенной по нормальному закону.
2. Докажем, что f (x), определенная данной формулой, - это плотность случайной величины, т.е. проверим, что
f ( x ) dx 1f ( x ) dx
1
2
2
( x a ) 2
x a
2
z
e 2 dx
z
e 2 dz
1
2
dx dz
2
z
e 2 dz
1
2
1
2 1,
2
3. здесь
использована формула Пуассона:z2
e 2 dz
2 .
4.
Найдем математическое ожидание M(X).M(X)
x f ( x ) dx
Замена :
( x a ) 2
2
x e 2 dx
x -a
z ; x a z ; dx dz.
a
2
1
2
z2
(a z) e 2 dz
1
2
z2
e 2 dz
1
2
z2
z e 2 dz
a
2 a.
2
Второй интеграл равен нулю, т.к. это интеграл от нечетной
функции по промежутку, симметричному относительно
начала координат.
5. Таким образом,
M( X) a6.
Найдем дисперсию D (X).D( X )
( x a ) 2 f ( x ) dx
Замена :
1
2
1
2
( x a ) 2
2
2
( x a ) e 2 dx
x -a
z ; x a z ; dx dz.
z2
2 2
z e 2 dz
Интегрируем по частям:
2
2
z2
z e 2 z dz
u z;
z2
dv e 2 z dz
du dz ;
z2
v e 2
7.
Тогда получимz
z
2
ze 2
e 2 dz
2 2 .
2
2
2
2
2
D( X )
2
Таким образом параметр в нормальном распределении –
это среднее квадратическое отклонение.
8.
9.
Исследуем кривую Гаусса1
y f(x)
2
1). Область определения
2). f (x) > 0
3). f ( x ) 0 при x
4). f (x)
1
2
( x a ) 2
2
2
e
x
( x a ) 2
2( x a )
2
2
e
;
2
2
f ( x ) 0 при x a
10.
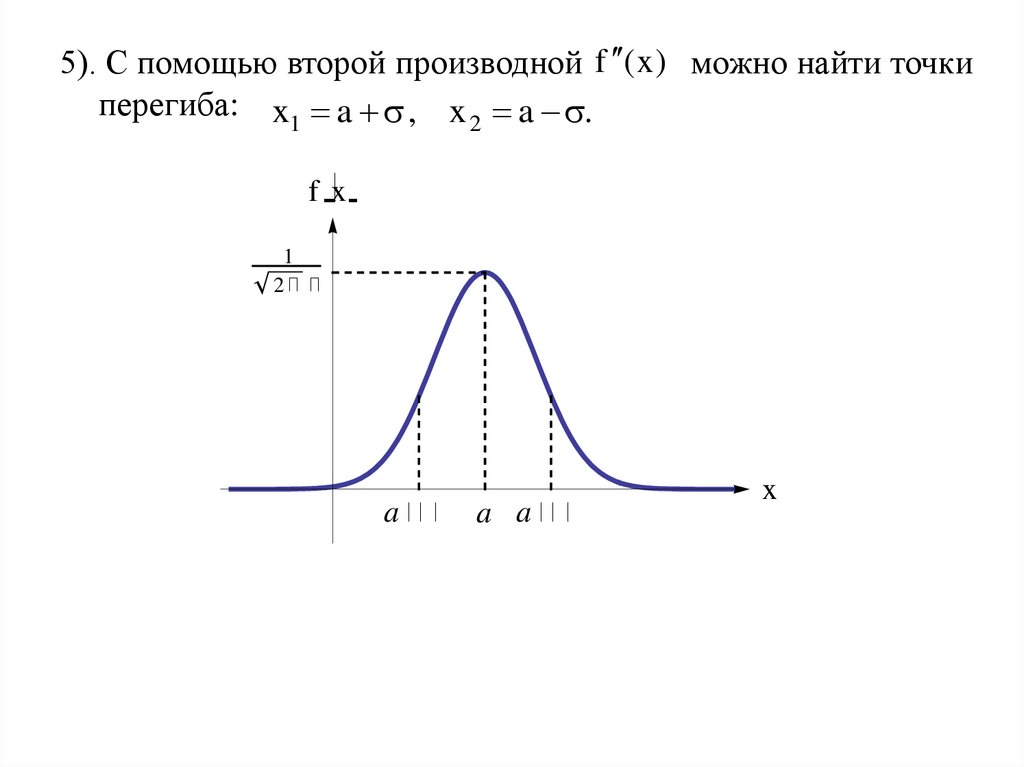
5). С помощью второй производной f ( x ) можно найти точкиперегиба: x1 a , x 2 a .
fx
1
2
a
a a
x
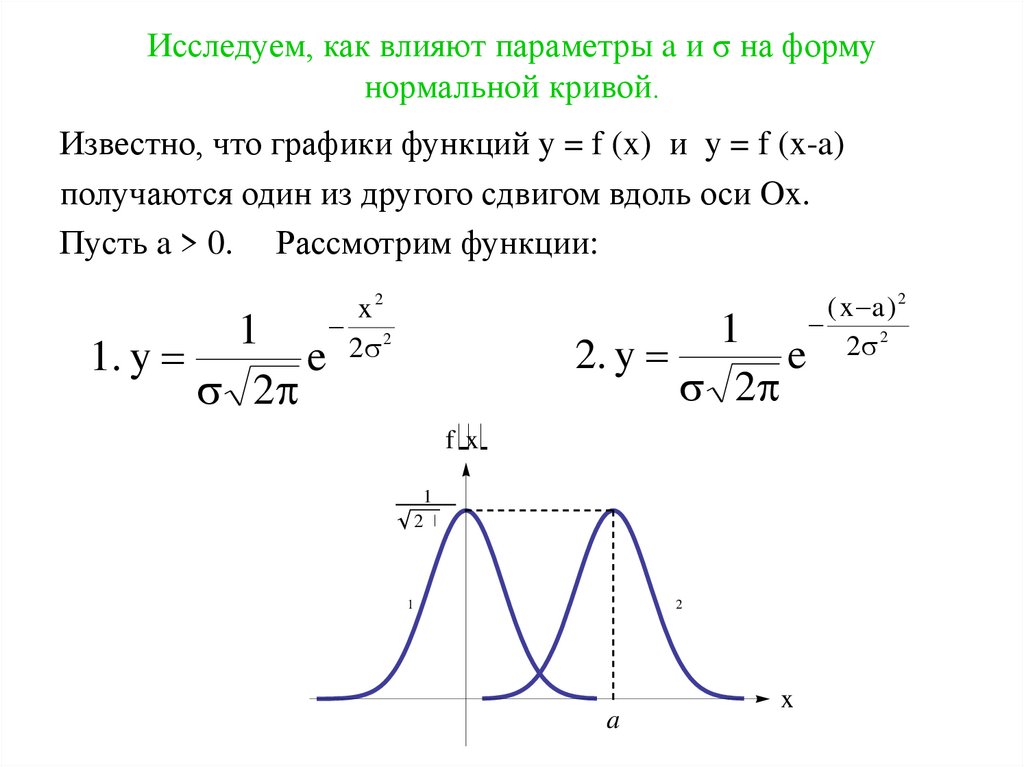
11. Исследуем, как влияют параметры a и σ на форму нормальной кривой.
Известно, что графики функций y = f (x) и y = f (x-a)получаются один из другого сдвигом вдоль оси Ox.
Пусть a > 0. Рассмотрим функции:
1
1. y
2
x2
2
e 2
1
2. y
2
( x a ) 2
2
2
e
fx
1
2
1
2
a
x
12.
Таким образом, график второй функции получается изграфика первой сдвигом вдоль оси Ox на а единиц вправо,
если a > 0, и – влево, если a < 0.
Отсюда следует, что график второй функции симметричен
относительно прямой x = a.
Значит, изменение параметра а влияет лишь на сдвиг
кривой и не влияет на ее форму.
13.
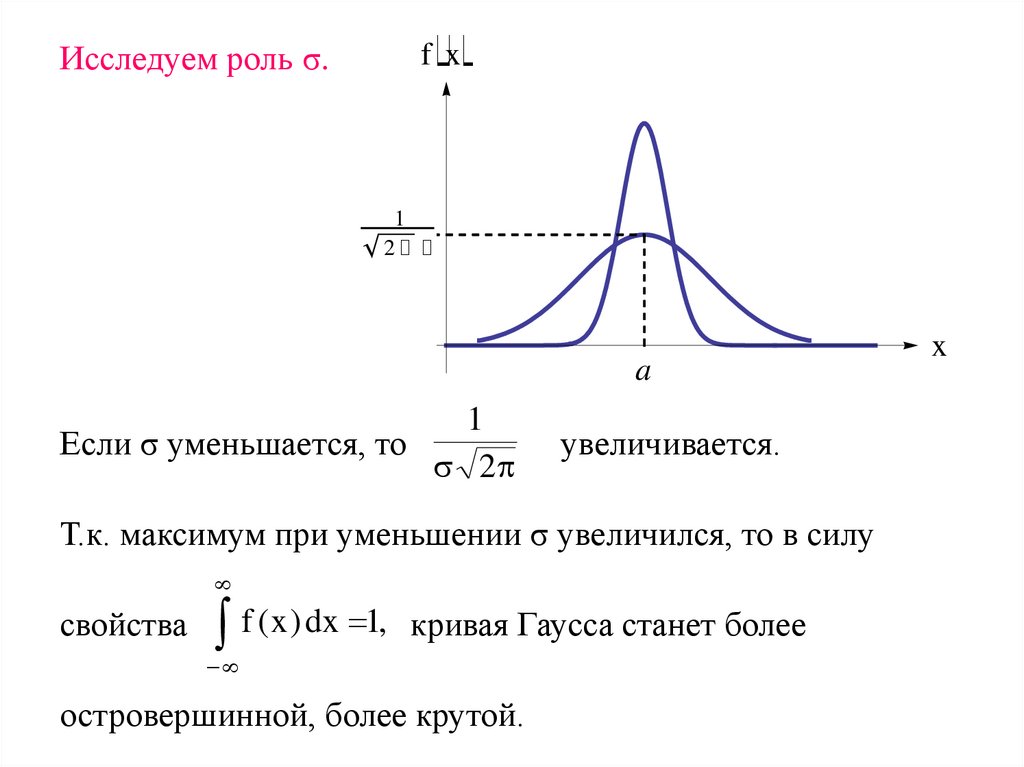
Исследуем роль σ.f x
1
2
a
1
Если σ уменьшается, то
2
увеличивается.
Т.к. максимум при уменьшении σ увеличился, то в силу
свойства
f (x ) dx 1, кривая Гаусса станет более
островершинной, более крутой.
x
14.
Это согласуется с вероятностным смыслом параметра σ (прималом σ значения случайной величины концентрируются
около математического ожидания).
15. Функция распределения нормально распределенной случайной величины.
По формуле предыдущей лекцииx
x
( t a ) 2
2
2
e
dt
1
F( x ) f ( x ) dx
2
t -a
z ; t a z ; dt dz;
x -a
при t x z
Замена :
x a
1
2
2
z
e 2 dz
x a
1
2
z2
e 2 dz
16.
Разделим промежуток интегрирования точкой 0 на два, тогдаинтеграл будет равен сумме двух интегралов:
0
1
2
1
2 0
x a
2
z
e 2 dz
1
2 0
z2
x a
x a
2
e dz
( )
2
так как
z2
e 2 dz
x t
e 2 dt ( x ),
1
2 0
1
x a
.
2
1
( )
2
17.
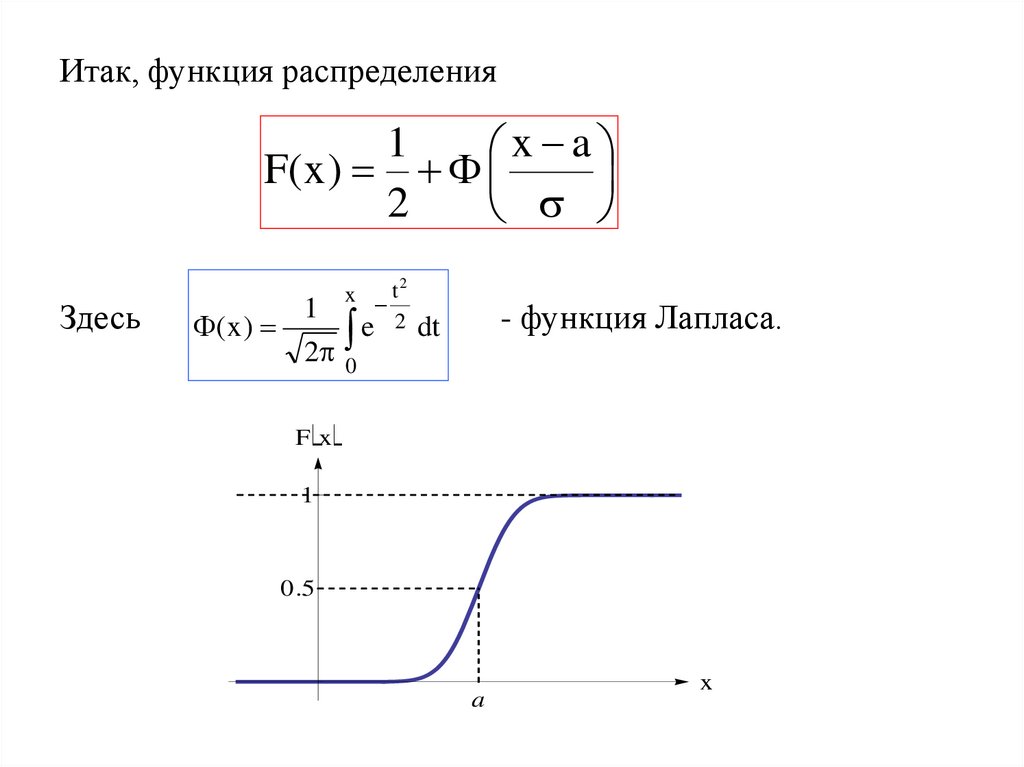
Итак, функция распределения1
x a
F( x )
2
2
Здесь
x t
e 2 dt
1
( x )
2 0
- функция Лапласа.
Fx
1
0.5
a
x
18. Вероятность попадания нормально распределенной случайной величины в заданный интервал.
Пусть случайная величина X распределена по нормальномузакону. Требуется найти вероятность, что она попадет в
интервал ( , ).
1
a 1
a
P( X ) F( ) F( )
2
2
так как
1
x a
F( x )
2
a
a
.
19.
Следовательно,a
a
P( X )
2
Здесь
( x )
x t
e 2 dt
1
2 0
- функция Лапласа.
20. Правило трех сигм
(3 ).Найдем вероятность того, что модуль отклонения нормально
распределенной случайной величины от ее математического
ожидания не превосходит утроенного среднего
квадратического отклонения, то есть
P(| X a | 3 ) ?
21.
ИмеемP(| X a | 3 ) P(a 3 X a 3 )
a 3 a
a 3 a (3) ( 3) 2 (3) 0,9973
Эта вероятность очень велика (близка к 1), то есть
осуществление исходного неравенства будет наблюдаться в
99,73% всех случаев – “практически всегда”.
Таким образом, модуль отклонения нормально
распределенной случайной величины от ее математического
ожидания практически не превосходит 3 . Это и есть
правило трех сигм.
22. Биномиальный закон распределения
Так называется закон, устанавливающий распределениевероятностей дискретной случайной величины X -числа
появлений события A при n повторных испытаниях, если
вероятность p появления события A в одном испытании для
всех испытаний постоянна.
23. Биномиальное распределение описывается формулой Бернулли
P( X m) Pn (m) Cnm p mq n m , q 1 pЧто означает Pn (m) (из предыдущих лекций)?
X
P
n
0
qn
n
P ( X m) C p q
m 0
m 0
m
n
m
n m
1
…
1 1 n 1
…
Cn p q
m
…
m m n m
…
Cn p q
n
pn
q n Cn1 p1q n 1 Cn2 p 2 q n 2 ... Cnm p m q n m ... p n (q p ) n 1
24. Математическое ожидание и дисперсия
1.1, 2 ,..., n
i
0
1
P
q
p
i2
0
1
P
q
p
M ( i ) 0 q 1 p p
M ( i2 ) p
D( i ) M ( i2 ) [M ( i )]2 p p 2 p(1 p) pq
25. Продолжение. Случайная величина
nX i
i 1
1.
n n
M ( X ) M i M ( i ) np
i 1 i 1
n n
D( X ) D i D( i ) npq
i 1 i 1
26. Закон распределения Пуассона
1.P ( X m)
me
m!
np
M ( X ) lim np lim
n
n
D( X ) lim npq lim q lim (1 p) lim 1
n
n
n
n
n
так как
p
n
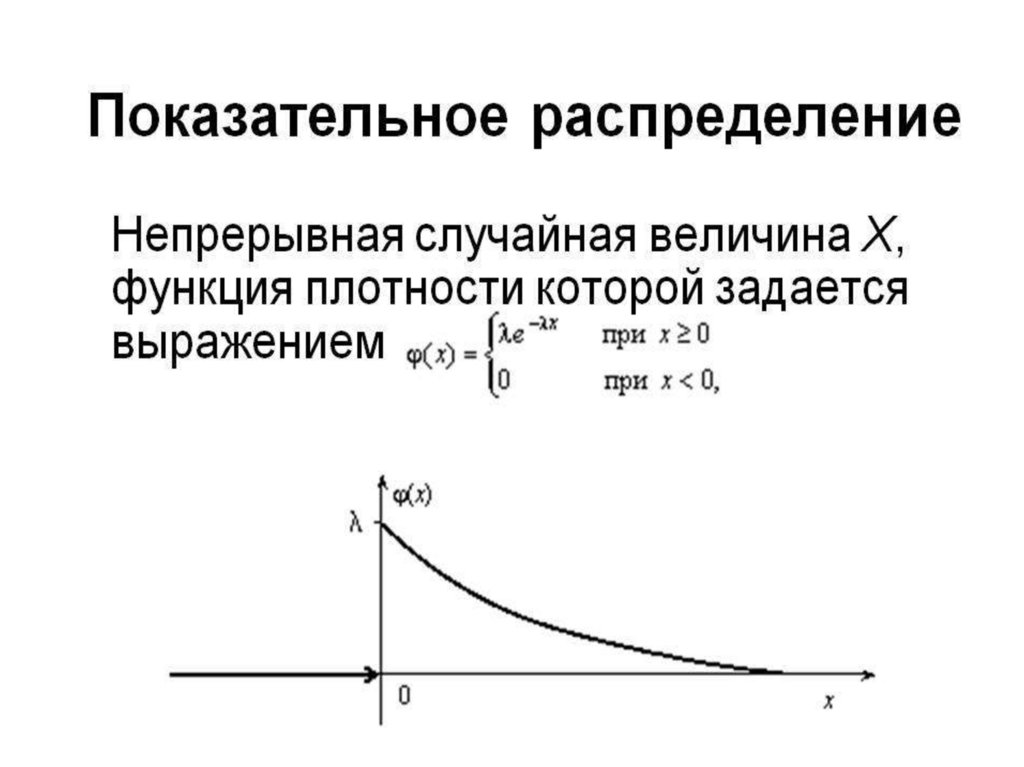
27. Показательное распределение
1.0, x ( ,0)
f ( x) x
ke , x [0, )
0
1 f ( x)dx ke
x
A
dx k lim e
A
0
x
1 x A
dx k lim
e
0
A
k
k
k
lim [e A 1]
( 1)
A
k
1, k
0, x ( ,0)
f ( x) x
e , x [0, )
28.
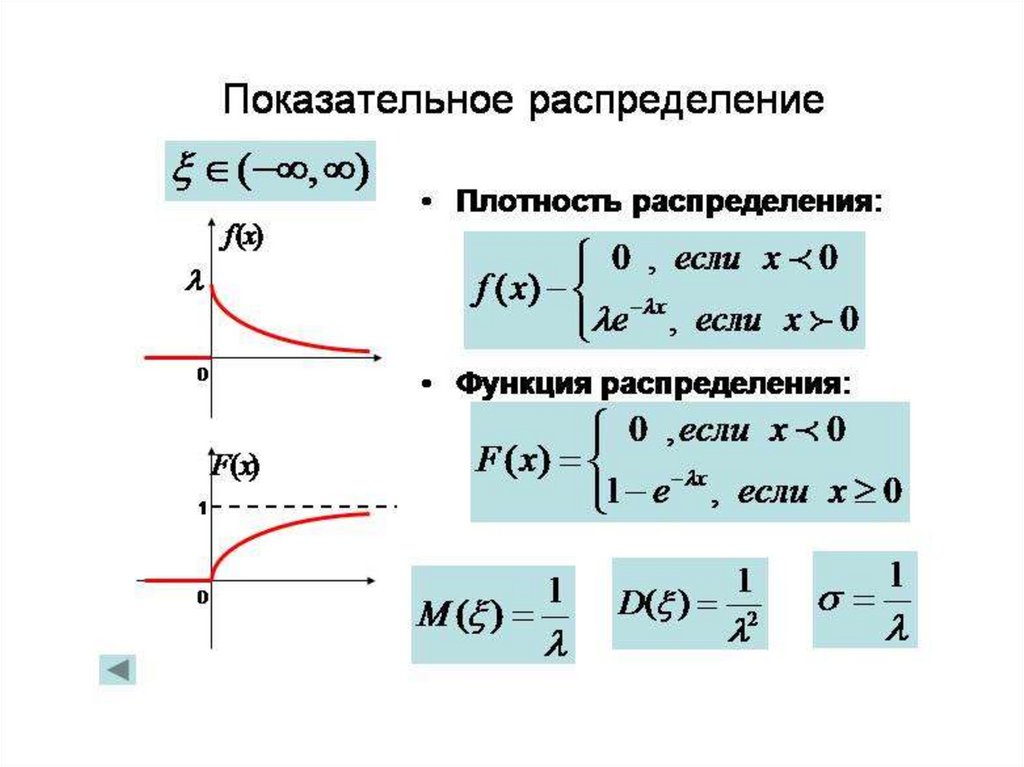
29. Функция распределения
2.1 t x
x
x
F ( x) e dt
e
(
e
1)
1
e
0
0
x
t
0, x ( ,0)
F ( x)
x
1
e
, x [0, )
30.
31. Числовые характеристики
1.0
M ( X ) x f ( x)dx x e
dv e x dx
1 x
du dx v
e
u x
x
A
dx lim xe x dx
A
b
0
b
udv uv vdu
b
a
a
a
x x A 1 A x
1
1 1
A A 1 x A
lim e
e dx lim e 2 e
lim
2
0
A
A
A 2 e A
0
0
Объясните, почему
A A
lim e 0
A
M (X )
1
32. Продолжение.
2. Дисперсия.D( X ) M ( X ) [ M ( X )] x e
2
2
2
0
D( X )
1
2
x
dx
1
2
1
2
33. Случайная величина T - время безотказной работы прибора
распределена по показательному законуF (t ) 1 e t
F (t ) P(T t ) определяет вероятность отказа за время t.
Следовательно, вероятность безотказной работы за время t
равна вероятности противоположного события:
Pн (t ) P(T t ) 1 F (t ) 1 (1 e t ) e t
Pн (t ) e t называется функцией надежности,
- интенсивность отказов.



























 mathematics
mathematics








