Результаты решения стационарных уравнений. Квантовые числа

1.

Результаты решения стационарных уравнений.
Квантовые числа.
1
Квантование полной энергии электрона:
me Z 2e4 1
En
,
2
2
2
(4πε 0 ) 2 n
n 1, 2,3,
( n Главное квантовое число)
2 Квантование квадрата орбитального момента импульса электрона:
Ll 2 l (l 1) 2 ,где l 0,1, 2,3, , (n 1) ( l Орбитальное квантовое число)
3
Квантование проекции момента импульса электрона на выделенное
направление в пространстве (ось Z):
Lz ml , где ml 0, 1, 2, 3, , l ( ml Магнитное орбитальное
квантовое число)
4
Волновые функции стационарных состояний и их зависимость от квантовых
E
чисел (n, l , m) имеет вид
i t
ψ n , l , m (r ,θ, φ) Rn , l (r )Yl , m (θ, φ) e
Отметим, что стационарное состояние в квантовой механике – это не такое состояние,
которое вообще не зависит от времени, а такое состояние, которое зависит от времени
по приведенному экспоненциальному закону.

2.

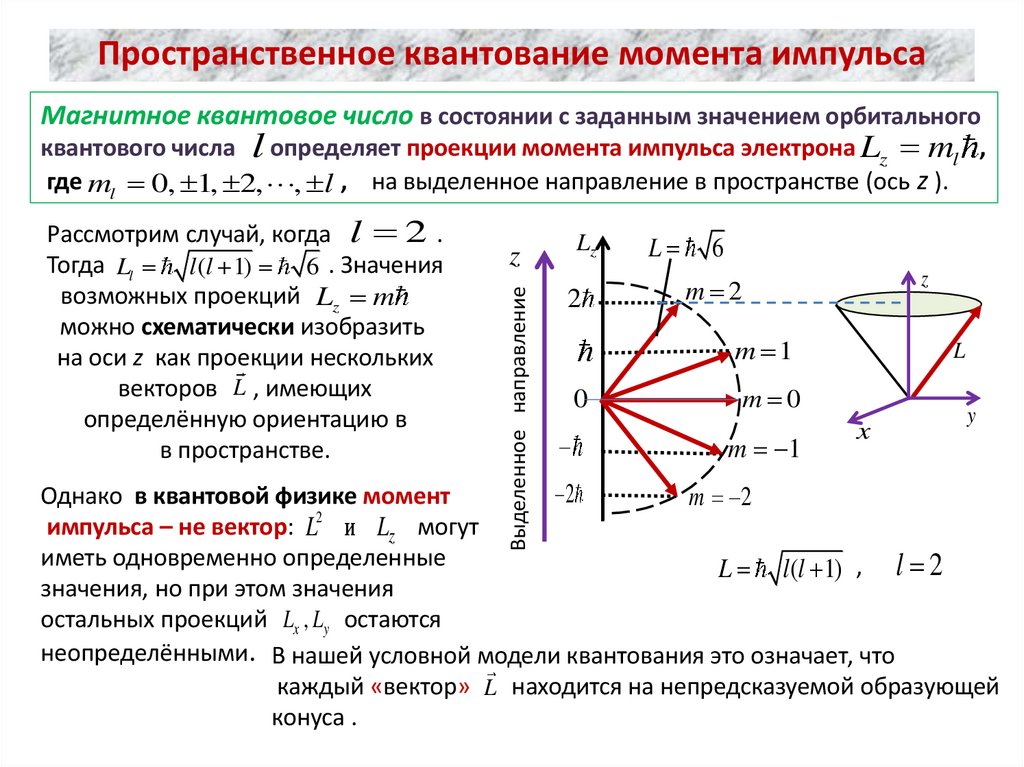
Пространственное квантование момента импульса
Магнитное квантовое число в состоянии с заданным значением орбитального
квантового числа l определяет проекции момента импульса электрона Lz ml ,
где ml 0, 1, 2, , l , на выделенное направление в пространстве (ось z ).
Lz
z
Выделенное направление
Рассмотрим случай, когда l 2 .
Тогда Ll l (l 1) 6 . Значения
возможных проекций Lz m
можно схематически изобразить
на оси z как проекции нескольких
векторов L , имеющих
определённую ориентацию в
в пространстве.
2
L
6
z
m 2
m 1
0
L
m 0
m 1
x
y
2
Однако в квантовой физике момент
m 2
2
импульса – не вектор: L и Lz могут
иметь одновременно определенные
L l (l 1) , l 2
значения, но при этом значения
остальных проекций Lx , Ly остаются
неопределёнными. В нашей условной модели квантования это означает, что
каждый «вектор» L находится на непредсказуемой образующей
конуса .

3.

Квантовые состояния электрона в атоме водорода
Для обозначения квантовых состояний с заданным
значением орбитального квантового числа l
используют следующие обозначения:
Значение l :
Символ состояния :
0
s
1
p
2
d
3
f
p - состояния
Перед символом состояния l указывается значение
главного числа
, например,
S - состояния
n
1s , 2s , 2p, 3d, …

4.

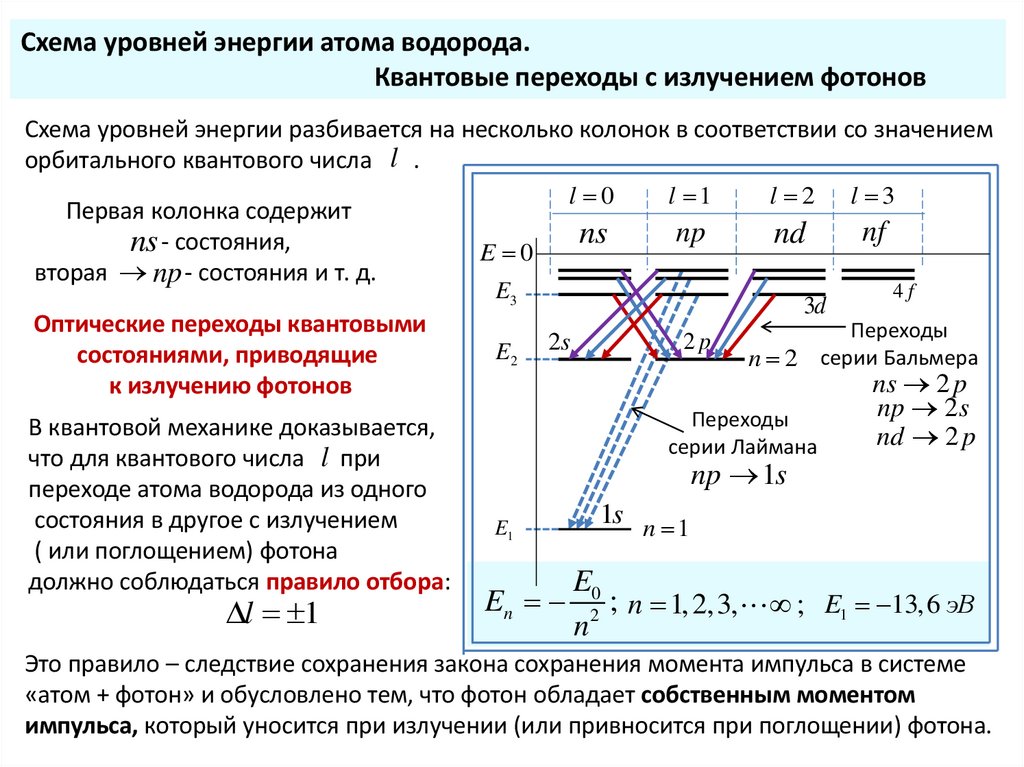
Схема уровней энергии атома водорода.
Квантовые переходы с излучением фотонов
Схема уровней энергии разбивается на несколько колонок в соответствии со значением
орбитального квантового числа l .
l 0
l 1
l 2 l 3
Первая колонка содержит
nf
np
nd
ns
ns - состояния,
E 0
вторая np - состояния и т. д.
4f
E3
3d
Оптические переходы квантовыми
Переходы
2
p
2s
E2
состояниями, приводящие
n 2 серии Бальмера
ns 2 p
к излучению фотонов
np 2 s
Переходы
В квантовой механике доказывается,
nd 2 p
серии Лаймана
что для квантового числа l при
np 1s
переходе атома водорода из одного
1s n 1
состояния в другое с излучением
E1
( или поглощением) фотона
должно соблюдаться правило отбора:
E0
l 1
En
n
2
; n 1, 2,3, ; E1 13, 6 эВ
Это правило – следствие сохранения закона сохранения момента импульса в системе
«атом + фотон» и обусловлено тем, что фотон обладает собственным моментом
импульса, который уносится при излучении (или привносится при поглощении) фотона.

5.

Схема уровней энергии в атомах щелочных металлов
E
Атом лития 37 Li
n=4
4p
4s
1
Атом 1 H
n=3
3p
3s
2p
2s
3d
n=2
Состояние каждого электрона в
многоэлектронном атоме
в первом приближении
определяется набором
квантовых чисел: ( n, l, m, ms )
В отличие от атома водорода,
энергия электронов зависит не
только от главного квантового
n
числа
, но и от орбитального
квантового числа l .
Причина зависимости энергии от l в том, что состояния с разными
распределениями плотности заряда, обладающие или не обладающие
сферической симметрией, по-разному экранируют заряд ядра для более
возбужденных состояний.
Электроны в атоме взаимодействуют между собой и с ядром ,
поэтому электрическое поле не является кулоновским.

6.

Взаимодействие магнитных моментов в атоме.
В многоэлектронном атоме каждый из N электронов
обладает орбитальным L i и спиновым S i моментами
импульса и магнитными моментами i и s ,i , которые
им соответствуют.
В результате взаимодействия магнитных
моментов отдельных электронов в атоме происходит
их сложение (по правилам квантовой механики) в
результирующий магнитный момент атома J ,
которому соответствует полный механический
момент LJ (суммарный момент импульса
многоэлектронного атома).
В легких и средних атомах встречается
LS - связь.

7.

LS-связь в легких и средних атомах
1 В результате наиболее сильного взаимодействия
орбитальных магнитных моментов отдельных
электронов образуются суммарный орбитальный
магнитный момент L и механический момент
2
всех электронов в атоме.
LL
L( L 1)
L - орбитальное
квантовое число атома
(целое число либо ноль)
В результате менее сильного взаимодействия
спиновых магнитных моментов отдельных
LS S (S 1)
электронов образуется суммарный магнитный
S – квантовое число
спиновый момент S и суммарный спин
спина атома
всех электронов в атоме.
Если в атоме четное число электронов, то квантовое число S является целы числом,
либо равно нулю. При нечетном числе электронов квантовое число S принимает
полуцелые значения.
3
Наиболее слабое спин-орбитальное взаимодействие
между магнитными моментами S и L приводит
к образованию результирующего магнитного
момента J и механического момента всего атома
LJ
J ( J 1)
Квантовое число J для заданной пары квантовых чисел L и S
принимает значения: J L S , L S 1, L S 2, , L S .

8.

Обозначение квантовых состояний
многоэлектронного атома
Энергия многоэлектронного атома зависит от всех квантовых
чисел n, L, S , J . Квантовое состояние атома при известном n
символически записывается в виде:
Символ:
(2 S 1)
" L " J
(" L ")
где под
понимается одна из следующих букв (S,P, …) в
схеме обозначений:
Квантовое число L : 0
Буква : S
1
P
2
D
3 ...
F ...
J L S , L S 1, L S 2, , L S .

9.

Заполнение уровней энергии электронами атомах
В одноэлектронном приближении
пренебрегается взаимодействием
между электронами и каждый из
них характеризуется набором из
4-х квантовых чисел:
Главное квантовое число:
nn 1,1,2,3,
2,3 ;
Орбитальное квантовое
число: l 0,1, 2, , ( n 1) ;
Квантовое число проекции
орбитального момента Ll , z
m 0, 1, 2, , l ;
Квантовое число проекции
спина LS , Z : mS (1 2) .
Обозначение атомов:
Число нуклонов в ядре
Число протонов в ядре
A
Z
"
N
X (n l " )
Обозначение
Электронная
химического элемента конфигурация
В электронной конфигурации показывается
последовательное заполнение уровней
энергии с указанием : квантового числа n ;
квантового числа l в буквенном
обозначении: s (l 0), p (l 1),
и числа электронов N в этом состоянии.
Электронные конфигурации в атомах двух периодов таблицы Менделеева:
1
1
7
3
Li (1s 2 2 s1 )
14
7
4
2
H (1s1 )
9
4
2
2
1
Be (1s 2 2 s 2 ) 11
5 B (1s 2 s 2 p )
N (1s 2 2s 2 2 p 3 )
16
8
O (1s 2 2s 2 2 p 4 )
12
6
19
9
He (1s 2 )
C (1s 2 2s 2 2 p 2 )
F (1s 2 2s 2 2 p 5 )
20
10
Ne (1s 2 2s 2 2 p 6 )

10.

Заполнение уровней энергии электронами. Правила Хунда.
Заполнение электронами уровней энергии происходит с учетом принципа
Паули , исходя из требования минимума полной энергии атома в
соответствии с правилами Хунда.
Совокупность электронов с одинаковым значением квантового числа
n образуют
оболочку . Например, K – оболочка ( n 1 ); L – оболочка ( n 2 ) и т.д.
В оболочках имеются подоболочки, различающиеся значением орбитального
квантового числа l . Например, подоболочки 2 s, 2 p в L – оболочке.
Эмпирические правила Ф. Хунда (немецкий физик-теоретик, 1927г)
1 Наименьшая энергия в данной электронной конфигурации
реализуется при максимальном суммарном спине всех
электронов ( S Smax ) и при данном S max максимальном
орбитальном моменте атома ( L Lmax ) .
2 Для основного (не возбужденного) состояния квантовое
число полного механического равно J L S , если
подоболочка заполнена менее, чем наполовину.
В остальных случаях J L S .

11.

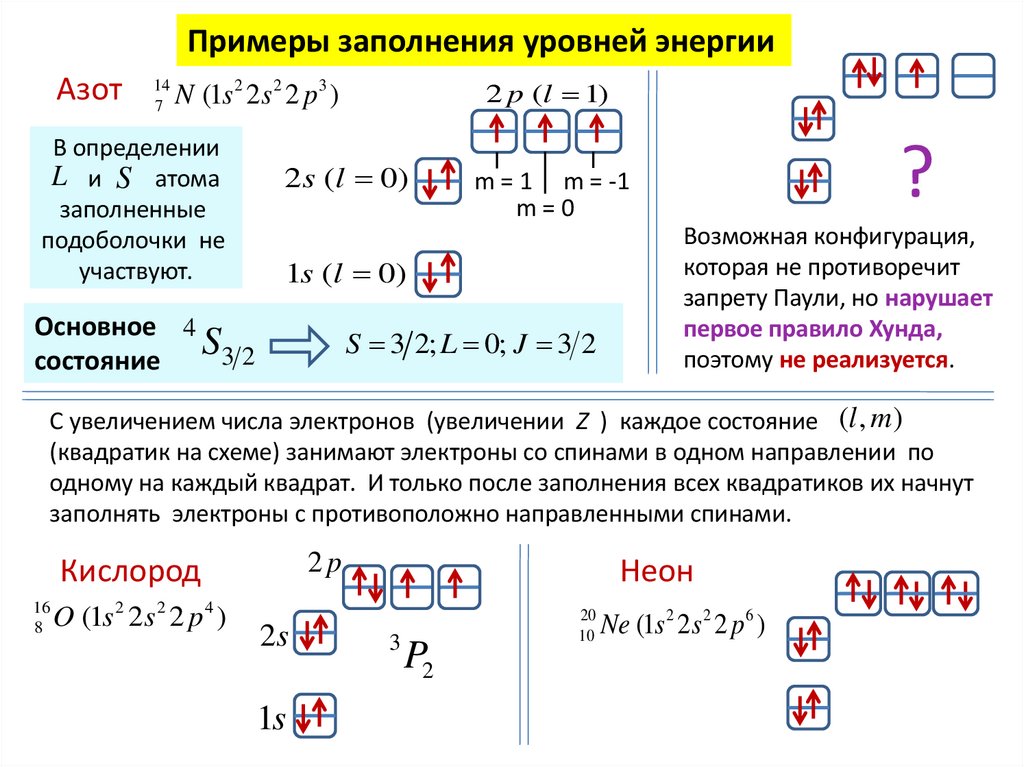
Примеры заполнения уровней энергии
Азот
14
7
2 p (l 1)
N (1s 2 2s 2 2 p 3 )
В определении
L и S атома
заполненные
подоболочки не
участвуют.
2 s (l 0)
1s (l 0)
Основное 4
S3 2
состояние
?
m = 1 m = -1
m=0
S 3 2; L 0; J 3 2
Возможная конфигурация,
которая не противоречит
запрету Паули, но нарушает
первое правило Хунда,
поэтому не реализуется.
С увеличением числа электронов (увеличении Z ) каждое состояние (l , m )
(квадратик на схеме) занимают электроны со спинами в одном направлении по
одному на каждый квадрат. И только после заполнения всех квадратиков их начнут
заполнять электроны с противоположно направленными спинами.
2p
Кислород
16
8
O (1s 2 2s 2 2 p 4 )
2s
1s
Неон
3
P2
20
10
Ne (1s 2 2s 2 2 p 6 )

12.

Заполнение уровней энергии электронами
на примере атома углерода
Конфигурация:
2
2
1s 2s 2 p
12
6
2
C
2p
1
1s 2 2s 2 2 p 2
2s
m=1
m = -1
m=0
3
1s
1
S0
1
D2
1
S0
D2
P0,1,2
3
P2
3
P1
3
P0
Схема энергетических уровней
3
Наименьшей энергией обладает состояние P (максимальный спин), далее следует
состояние 1D2 , у которого L больше, чем у состояния 1S0 при равной
мультиплетности ( 2S 1 1 ).
Состояние 3 P вырождено, оно состоит из трех состояний P0 ; P1 ; P2
( в соответствии со значениями J L S , L S 1, , L S , имеющих одну и ту
же энергию, если пренебречь спин-орбитальным взаимодействием.
3
3
3
3
Спин-орбитальное взаимодействие снимает вырождение, расщепляя состояние P0,1,2
на 3 подуровня, среди которых основным состоянием является 3 P0 в соответствии
с правилами Хунда.

13.

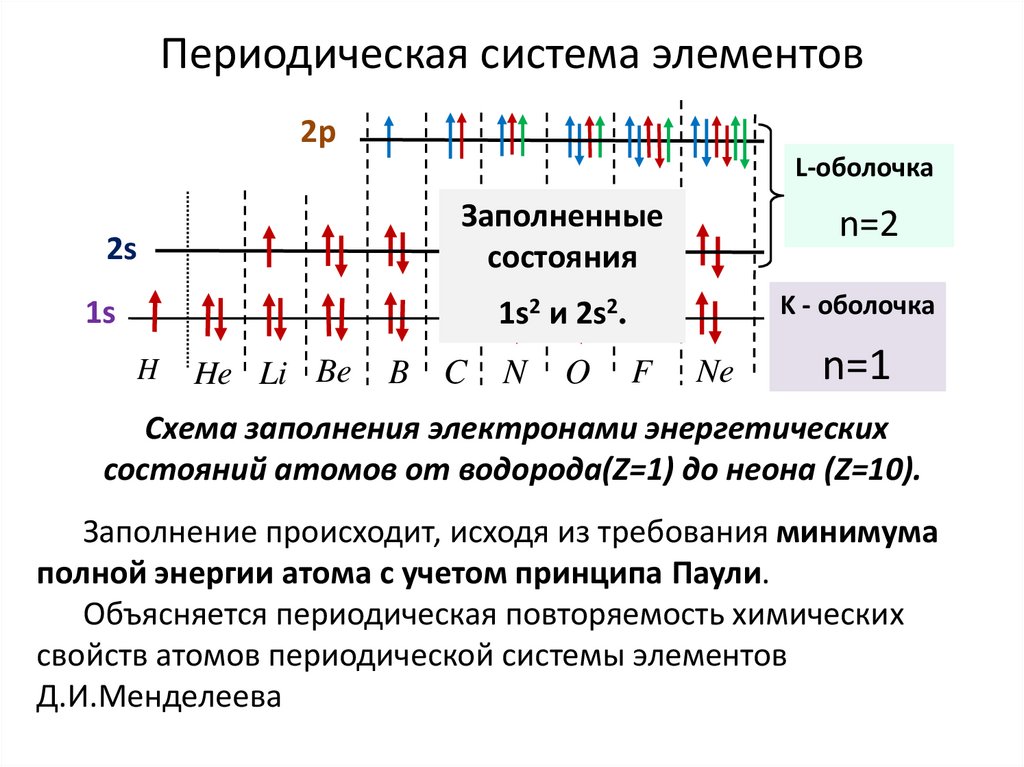
Периодическая система элементов
2p
L-оболочка
2s
Заполненные
состояния
n=2
1s
1s2 и 2s2.
K - оболочка
H
He Li Be
B C
N
O
F
Ne
n=1
Схема заполнения электронами энергетических
состояний атомов от водорода(Z=1) до неона (Z=10).
Заполнение происходит, исходя из требования минимума
полной энергии атома с учетом принципа Паули.
Объясняется периодическая повторяемость химических
свойств атомов периодической системы элементов
Д.И.Менделеева

14.

Правила отбора при оптических переходах
Квантовая теория, исходя из закона сохранения моментов импульса,
обосновывает правила отбора для разрешенных оптических переходов
атома из одного квантового состояния в другое.
Переходы с излучением подчиняются следующим правилам
изменения квантовых чисел:
S 0; L 0, 1; J 0, 1;
ms 0; mL 0, 1; mJ 0, 1
Переход из состояния с ( J нач 0 ) в состояние с ( J кон 0) запрещен.
Примеры.
2
Разрешенные переходы:
Запрещенные
переходы:
2
D3 2 2 P1 2 ;
D3 2 S1 2 ;
2
2
2
D5 2 P1 2 ;
2
F7 2 2 D5 2
2
F5 2 P3 2
2

15.

Излучение головной
спектральной линии серии
Бальмера в атоме водорода
по квантовой теории
Шредингера.
n 3
n 2
3s
3p
Учет релятивистских эффектов и
спин-орбитального взаимодействия
приводит к сдвигу уровней энергии и
к их тонкому расщеплению.
В мультиплете головной линии серии
Бальмера содержится 5 спектральных
линий
2
3d
2
2s
2p
656,3нм
s1 2
n 2
2
s1 2
2
P3 2
2
2
P3 2
2
P1 2
P1 2
D5 2
2
D3 2
5 10 5 эВ

16.

Магнитный момент многоэлектронного атома
Квантово-механический расчет приводит к следующему соотношению
между механическим моментом и результирующим магнитным
моментом всех электронов в атоме:
e
J
g LJ ; g J ( J 1) ; g 1 J ( J 1) S ( S 1) L( L 1)
J
Б
2me
2 J ( J 1)
где множитель g называется
физик-теоретик).
LJ
L
S
LS
LL
J
J
g-фактором Ланде (А.Ланде – немецкий
e
L
LL
2me
LL
L( L 1)
e
S 2
LS
2me
LS
S (S 1)
S 2 Б S (S 1)

17.

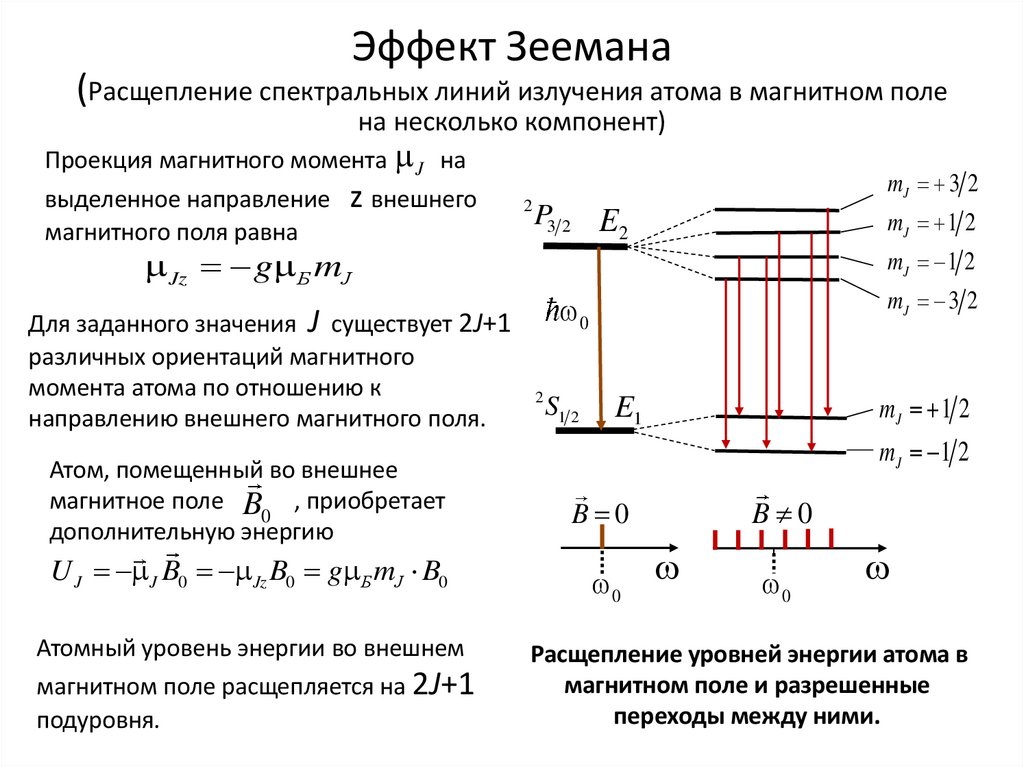
Эффект Зеемана
(Расщепление спектральных линий излучения атома в магнитном поле
на несколько компонент)
Проекция магнитного момента J на
выделенное направление
магнитного поля равна
z внешнего
2
mJ 3 2
P3 2 E
2
mJ 1 2
Jz g Б mJ
Для заданного значения J существует 2J+1
различных ориентаций магнитного
момента атома по отношению к
направлению внешнего магнитного поля.
Атом, помещенный во внешнее
магнитное поле B , приобретает
0
дополнительную энергию
U J J B0 Jz B0 g Б mJ B0
Атомный уровень энергии во внешнем
магнитном поле расщепляется на 2J+1
подуровня.
mJ 1 2
mJ 3 2
0
2
S1 2
mJ 1 2
E1
mJ 1 2
B 0
B 0
0
0
Расщепление уровней энергии атома в
магнитном поле и разрешенные
переходы между ними.