Термы двухатомных молекул. Квантовые числа и термы атомов. Термы основного состояния. Лекция 13

1. Лекция 13

Термы двухатомных молекул. Квантовые
числа и термы атомов. Термы основного
состояния. Таблица микросостояния для
конфигурации np2

2.

Одной из главных проблем локального подхода к построению структурной
модели атома является установление явного вида одноэлектронных
орбиталей, описывающих отдельные электроны атома.
Самый
простой!
Использование системы стационарных состояний атома водорода
(одноэлектронного атома) в качестве модели многоэлектронного атома
+
1s
+
+
++
2s
1s
2s
Модель является весьма грубой:
полное пренебрежение взаимодействиями электронов друг с другом
(электромагнитные и квантовые)

3.

С другой стороны, данная модель позволяет полностью перенести на
многоэлектронный атом все характеристики атома водорода:
наблюдаемые электрона, такие как энергия Е, модули векторов
механических моментов — орбитального |L|, спинового |S| и полного |J|,
и их проекции — Lz, Sz, Jz ,
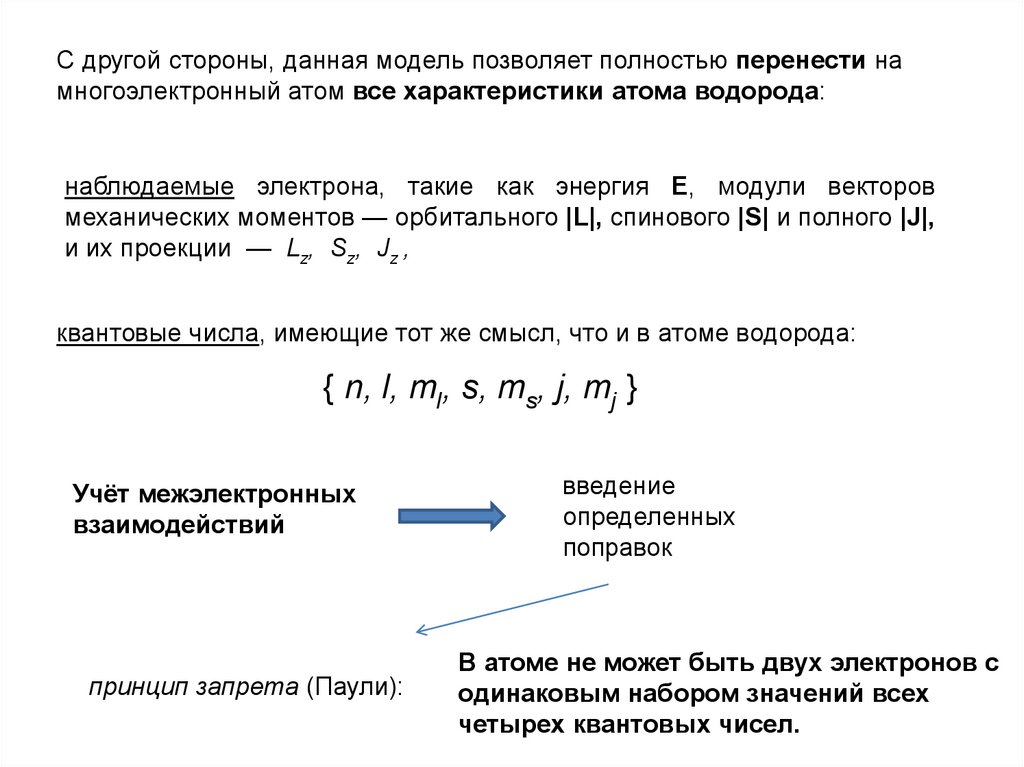
квантовые числа, имеющие тот же смысл, что и в атоме водорода:
{ n, l, ml, s, ms, j, mj }
Учёт межэлектронных
взаимодействий
принцип запрета (Паули):
введение
определенных
поправок
В атоме не может быть двух электронов с
одинаковым набором значений всех
четырех квантовых чисел.

4.

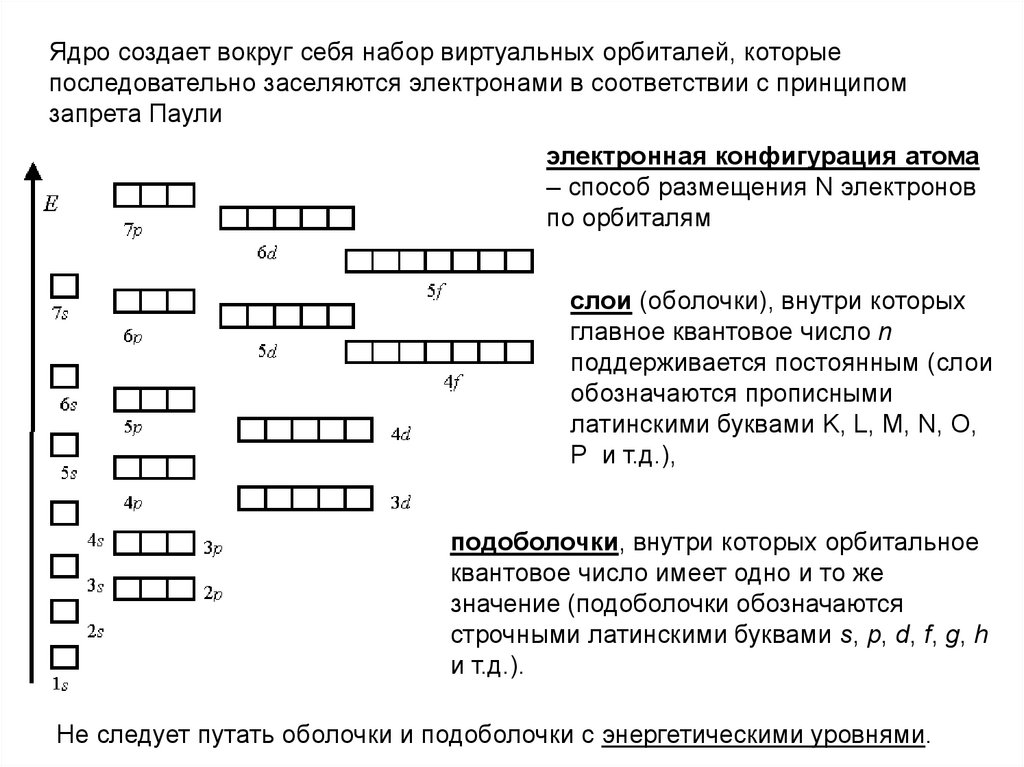
Ядро создает вокруг себя набор виртуальных орбиталей, которые
последовательно заселяются электронами в соответствии с принципом
запрета Паули
электронная конфигурация атома
– способ размещения N электронов
по орбиталям
слои (оболочки), внутри которых
главное квантовое число n
поддерживается постоянным (слои
обозначаются прописными
латинскими буквами K, L, M, N, O,
P и т.д.),
подоболочки, внутри которых орбитальное
квантовое число имеет одно и то же
значение (подоболочки обозначаются
строчными латинскими буквами s, p, d, f, g, h
и т.д.).
Не следует путать оболочки и подоболочки с энергетическими уровнями.

5.

Оболочки и подоболочки могут быть охарактеризованы двумя важными
параметрами:
заселенностью (конкретное число электронов в составе)
емкостью max (максимально возможное число электронов)
Емкость слоя
max = 2n2
Емкость подоболочки
max = 4l + 2
слои и оболочки
заполненные ( = max )
незаполненные ( < max )
Электронная конфигурация описывается электронной формулой
vi
(ni li )
Например, формула атома углерода имеет вид: (1s)2(2s)2(2p)2

6.

атомные термы
совокупность состояний атома, обладающих одной и той же
энергией, т.е. другими словами, энергетический уровень.
Полная энергия атома зависит от ряда параметров:
1. от орбитальных энергий и распределения электронов по атомным
орбиталям (электронной конфигурации);
2. от кулоновских межэлектронных взаимодействий (межэлектронного
отталкивания);
3. от магнитного спин-орбитального взаимодействия, обусловленного
взаимным влиянием магнитных моментов атома — орбитального и
спинового.
В результате, энергия атома зависит от величин глобальных механических
моментов ( |L|, |S|, |J| ) или, что то же самое, от значений соответствующих
квантовых чисел L, S и J

7.

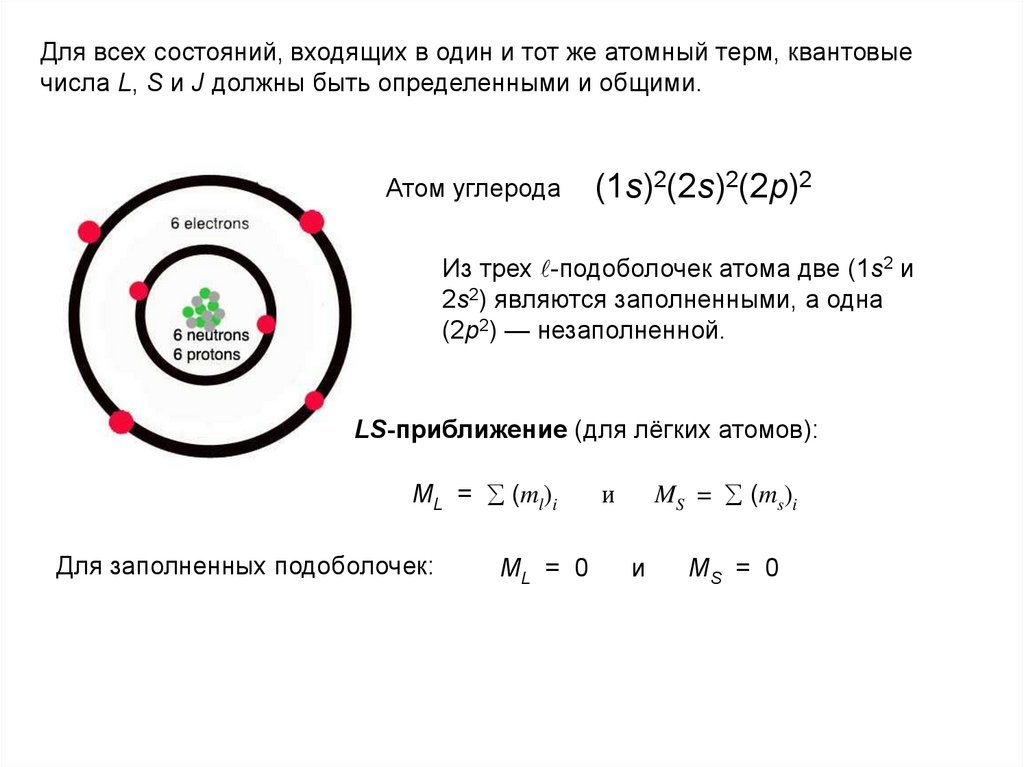
Для всех состояний, входящих в один и тот же атомный терм, квантовые
числа L, S и J должны быть определенными и общими.
Атом углерода
(1s)2(2s)2(2p)2
Из трех -подоболочек атома две (1s2 и
2s2) являются заполненными, а одна
(2р2) — незаполненной.
LS-приближение (для лёгких атомов):
ML = (ml)i
Для заполненных подоболочек:
ML = 0
MS = (ms)i
и
и
MS = 0

8.

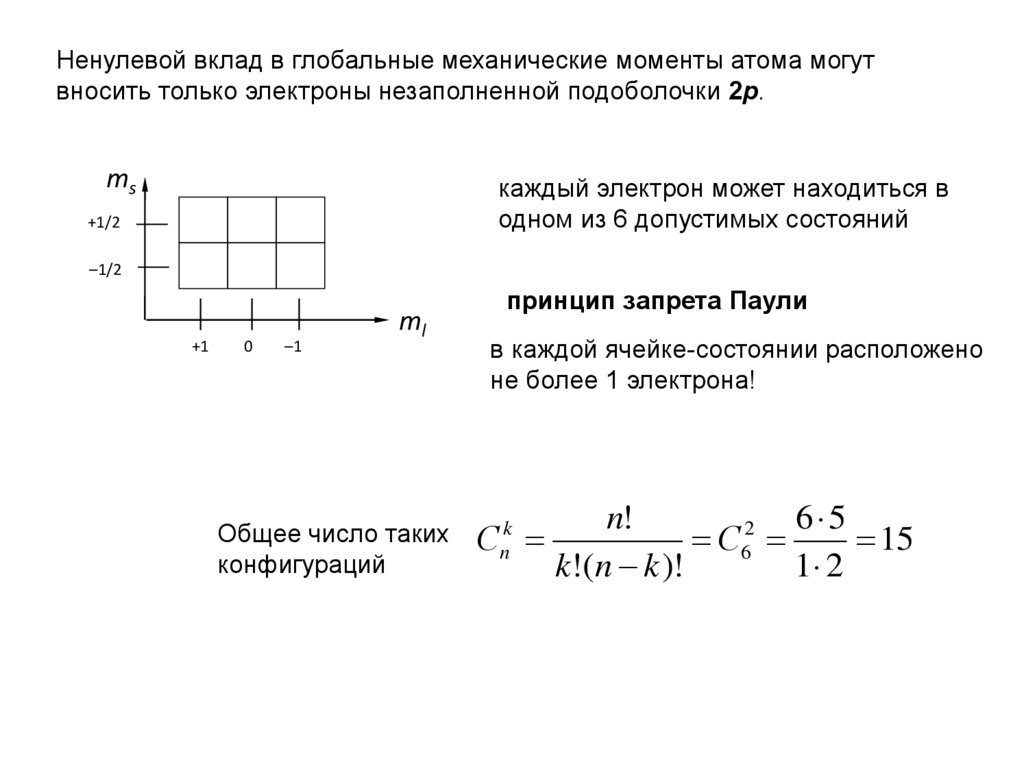
Ненулевой вклад в глобальные механические моменты атома могут
вносить только электроны незаполненной подоболочки 2р.
ms
каждый электрон может находиться в
одном из 6 допустимых состояний
+1/2
–1/2
+1
0
–1
ml
Общее число таких
конфигураций
принцип запрета Паули
в каждой ячейке-состоянии расположено
не более 1 электрона!
n!
6 5
2
С
С6
15
k!(n k )!
1 2
k
n

9.

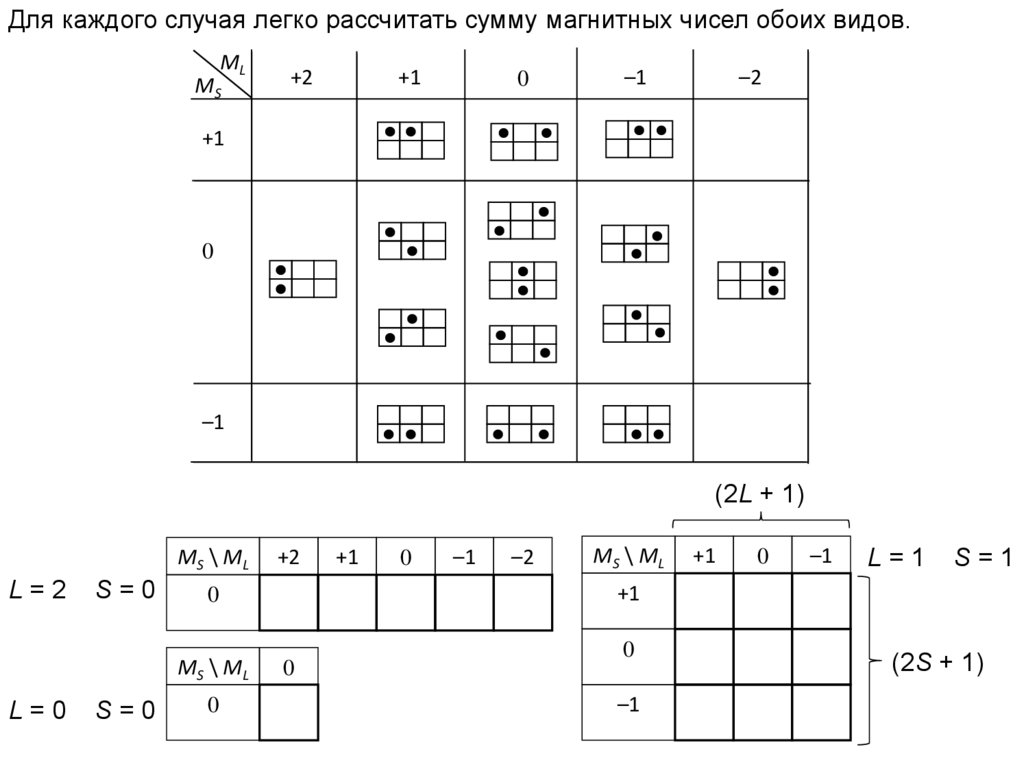
Для каждого случая легко рассчитать сумму магнитных чисел обоих видов.
ML
MS
+2
+1
0
–1
–2
+1
0
–1
(2L + 1)
MS \ ML
L=2
S=0
S=0
0
+1
0
–1
–2
MS \ ML
+1
0
–1
L=1
S=1
+1
0
MS \ ML
L=0
+2
0
0
–1
(2S + 1)

10.

1 терм
L=2
S=0
(+2,0)
2 Терм
L=1 S=1
3 терм
L=0
S=0
(+1,0)
(+1,+1)
(+1,0)
(+1,-1)
( 0,0)
( 0,+1)
( 0,0)
( 0,-1)
(-1,0)
(-1,+1)
(-1,0)
(-1,-1)
( 0,0)
(-2,0)
5 состояний
9 состояний
1 состояние
15 состояний, возможных для атома углерода
( L, S ) (2,0) 1D
2
Конфигурация ( p ) Термы ( L, S ) (1,1) 3P
( L, S ) (0,0) 1S

11.

Номенклатура термов в первую очередь учитывает эти два признака:
во-первых, величину орбитального момента импульса
во-вторых, величину спинового момента импульса
По величине суммарного L термы называются:
Число L : 0 1 2 3 4 5 ...
Терм :
S P D F G H ...
По величине суммарного спина S вводится мультиплетность, равная 2S+1
Число S :
1/ 2
1
3/ 2
2
5/ 2
...
Мультиплетность 2 S 1
2
3
4
5
6
...
Наименование
(дублет ) (триплет) (квартет) (квинтет) (секстет) ...
Результирующий символ
атомного терма
2 S 1
L

12.

Для всех состояний одного терма
– одна и та же пространственная
форма электронного облака.
энергия межэлектронного
отталкивания будет
одинакова
Зная принадлежность состояний к определенным термам, можно
предсказать их распределение по энергетической шкале
Правила Хунда
1 правило: минимальной энергией обладает терм с максимальной
мультиплетностью (значением квантового числа S).
2 правило: при равных мультиплетностях минимальной энергией
обладает терм с максимальным квантовым числом L
Так, для атома углерода минимальной энергией будут обладать 9
состояний терма 3P (1-е правило Хунда), а максимальной — 1
состояние терма 1S (2-е правило Хунда)

13. Учет спин-орбитального взаимодействия

Полная энергия атома будет зависеть от их взаимной
ориентации векторов L и S
Полный механический момент J
J = L + S, L + S – 1, ... | L – S |
Для атома углерода
1) терм 1S : L = 0
2) терм 3P : L = 1
3) терм 1D : L = 2
S = 0, J = 0
S = 1, J = 1 + 1 = 2, J = 1 + 0 = 1, и
S=0, J=2+0=2
J=1–1=0
3P (1)
0
1S
1S (1)
0
3P
3P (3)
1
3P (5)
2
1D
1D (5)
2

14.

Относительные энергии подтермов определяются 3-м правилом Хунда:
а) если подоболочка заполнена наполовину и менее ( 2l + 1), то
минимальная энергия соответствует подтерму с минимальным
значением квантового числа J,
а) если подоболочка заполнена более чем наполовину ( > 2l + 1), то
минимальная энергия соответствует подтерму с максимальным
значением квантового числа J.
Для атома углерода выполняется первое условие, и следовательно,
энергии подтермов соотносятся следующим образом:
3P
2
> 3P1 > 3P0
Число состояний в подтерме равно 2J + 1 и определяется числом
возможных ориентаций вектора J.
Все состояния подтерма имеют одинаковую энергию. Однако подтерм
также можно расщепить, если наложить внешнее магнитное поле. В этом
случае энергия будет зависеть от ориентации вектора полного момента
относительно внешнего поля.

15. Расщепление энергетических уровней спин-орбитальным взаимодействием

При рассмотрении этого эффекта широко используются две схемы: схема
j-j-взаимодействия и схема Рассела—Саундерса ( L-S –взаимодействия).
j-j-схема - спиновый угловой момент отдельного электрона
взаимодействует с орбитальным моментом с образованием суммарного
вектора j. Отдельные j суммируются и дают J полного углового момента
атома.
В схеме Рассела-Саундерса индивидуальные орбитальные угловые
моменты электронов ml взаимодействуют с образованием
суммарного
углового момента
(L). Взаимодействие спиновых моментов дает S.
Результирующий
угловой
момент,
включающий
спин-орбитальное
взаимодействие, обозначается J. Квантовое число J изменяется от L - S до L
+ S. Если подоболочки заполнены менее чем наполовину, то состоянию с
низшей энергией (терму основного состояния) соответствует минимальное
значение J.
В том случае, когда подоболочка заполнена более чем наполовину
состоянию низшей энергии сопоставляется максимальное значение J. Если
оболочка заполнена наполовину, существует только одно значение J,
поскольку L = 0.
Схема Рассела-Саундерса используется для d-элементов

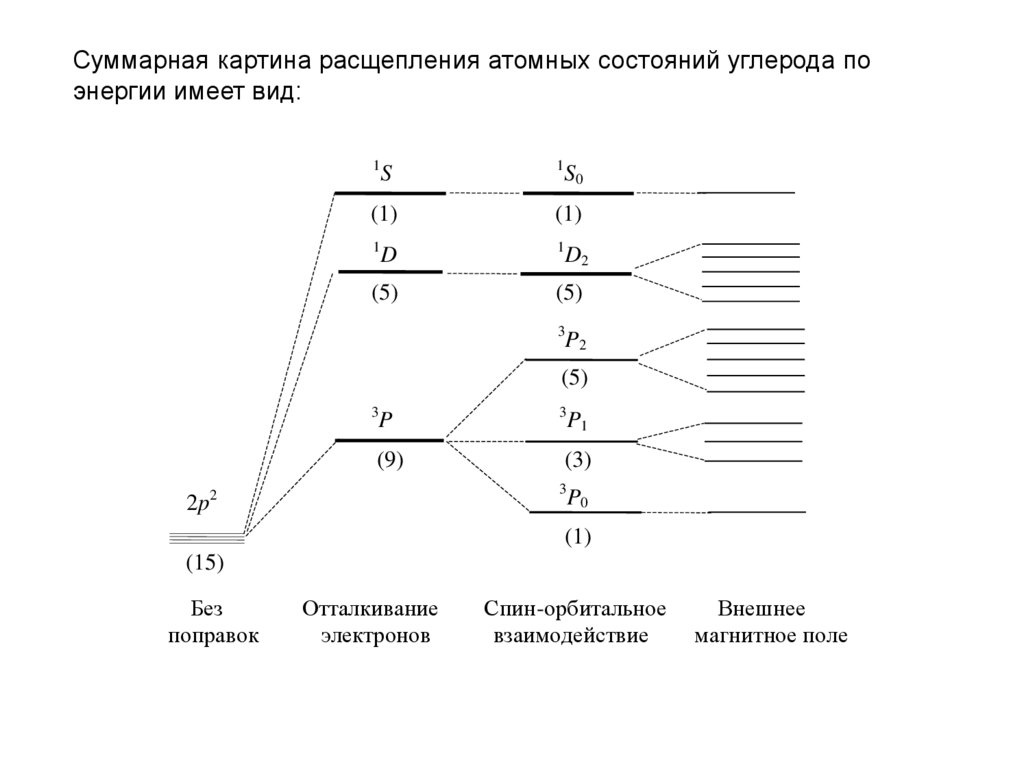
16.

Суммарная картина расщепления атомных состояний углерода по
энергии имеет вид:
1
S
1
(1)
(1)
1
D
1
(5)
(5)
S0
D2
3
P2
(5)
3
P
3
(9)
(3)
3
2p2
P1
P0
(1)
(15)
Без
поправок
Отталкивание
электронов
Спин-орбитальное
взаимодействие
Внешнее
магнитное поле