Квантовые числа. Лекция 5

1. Квантовые числа

2. Квантовые числа

Квантовыми числами называют целые
(0, 1, 2,...)
или полуцелые
1
3
5
( , , ,...)
2
2
2
числа, определяющие возможные
дискретные
значения
физических
величин,
которые
характеризуют
квантовые системы

3. Главное квантовое число n

Главное квантовое число n 1,2,3,...
Оно
определяет
уровни
энергии
электрона в атоме водорода
( z 1)
или водородоподобных ионах
m e Z
En
2
2
2
8 0 h n
4
2

4.

Атомы элементов характеризуются зарядом
ядра и равным ему числом электронов,
находящихся
на
определенных
энергетических уровнях.

5.

Эти
уровни
cоотносятся
с
главным
квантовым числом n, которое отражает
удаленность электронного слоя от ядра и
запас энергии электронов в этом слое: чем
больше значение n, тем «размазаннее»
электронное облако и больше энергия
электронов

6.

График зависимости
потенциальной
энергии
Еn
от
расстояния r между
электроном и ядром.
С возрастанием
главного квантового
числа n
увеличивается r, а
полная и
потенциальная
энергии стремятся к
нулю

7. Электронные квантовые слои

Число орбит в атоме элемента определяется
номером
периода
периодической
системы
Д.И.Менделеева. Поскольку периодов семь,
различают уровни энергии 1, 2, 3, 4, 5, 6, 7,
которые называют также квантовыми слоями и
обозначают прописными латинскими буквами.
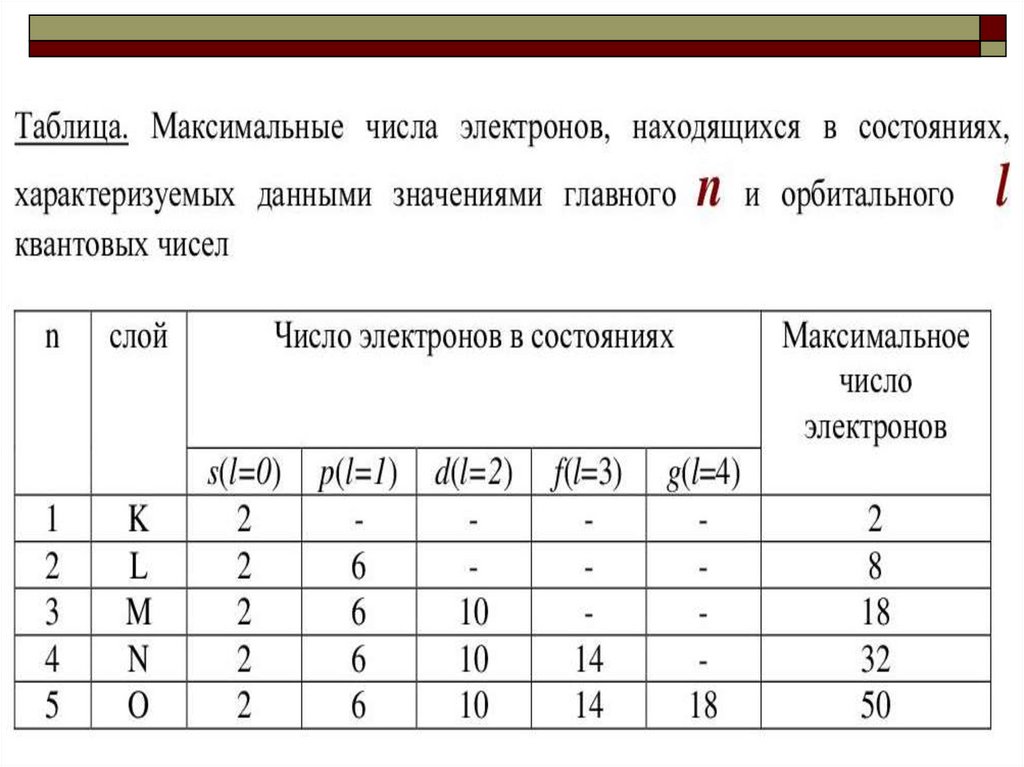
Максимальное число электронов в квантовом слое
(на
энергетическом
уровне)
соответствует
формуле n
= 2n2, где n – номер слоя.
max

8.

Энергетические уровни состоят
из
определенного
числа
подуровней:
первый уровень (К, n = 1) – из
одного подуровня (s),

9.

второй (L,
n = 2) – из двух (2s,2р),
третий (М,
(3s,3р,3d),
n = 3) – из трех
четвертый (N,
(4s,4р,4d,4f).
n = 4) – из четырех

10. Электронные квантовые слои

11. Примечание

У атомов элементов главных подгрупп
периодической таблицы Д.И.Менделеева
число электронов в последнем квантовом
слое равно номеру группы.
У атомов элементов побочных подгрупп
число электронов в последнем слое равно
двум (исключение составляют Сu, Ag, Au,
Cr, Ru, Rh, Pt – по одному электрону, у Pd
– ноль электронов).

12.

Подуровень характеризует побочное
(орбитальное) квантовое число l
Оно определяет форму электронного
облака и показывает запас энергии
электрона на подуровне.
Подуровни обозначаются буквами:
s, р, d, f, а также числами: 0, 1, 2, 3.

13. Орбитальное квантовое число l

орбитальное квантовое число
данном n принимает значения
при
(l = 0, 1, …, (n – 1)).
Это число характеризует
момент
импульса
Ll
относительно ядра
орбитальный
электрона
Ll l (l 1)

14. Таблица значений орбитального квантового числа и состояний электрона в атомах

значение l
0
1
2
3
4
5
6 7
состояние
s
p
d
f
g h l k

15.

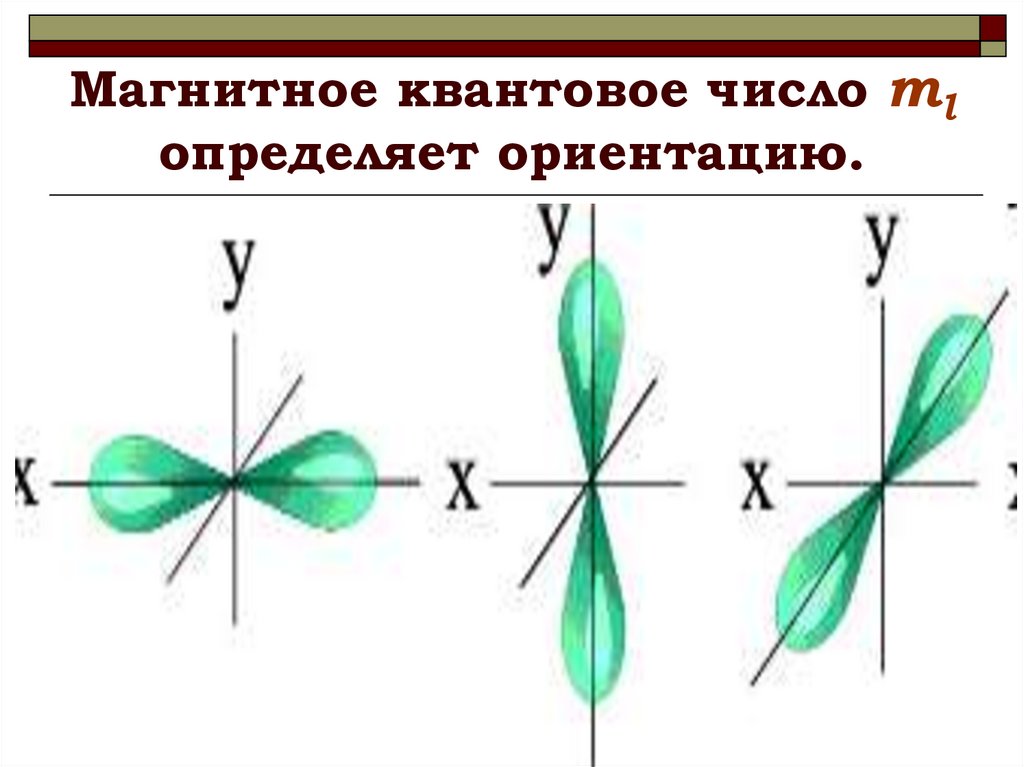
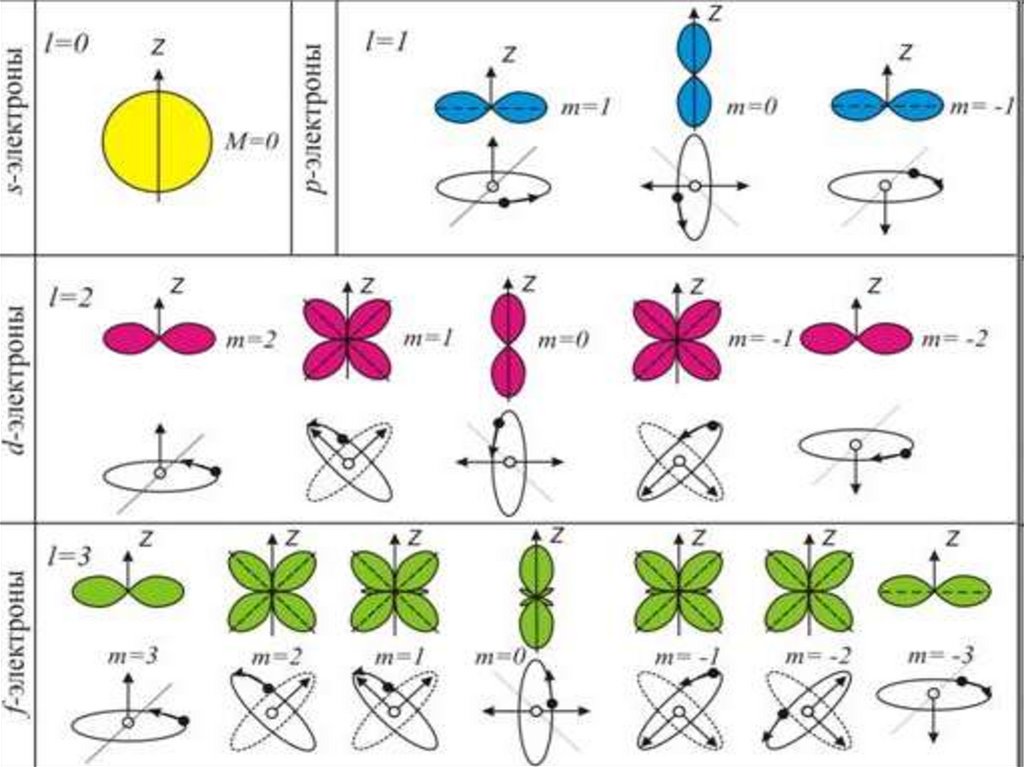
16. Магнитное квантовое число m

Магнитное
квантовое
число
принимает
значения: m = 0, ±1, ±2,…,±l
(l – орбитальное квантовое число) всего 2l 1
значений.
Это число определяет проекции орбитального
момента импульса электрона на некоторое
произвольно выбранное направление Z (или
направление внешнего магнитного поля)
Llz m

17. Магнитное квантовое число ml определяет ориентацию.

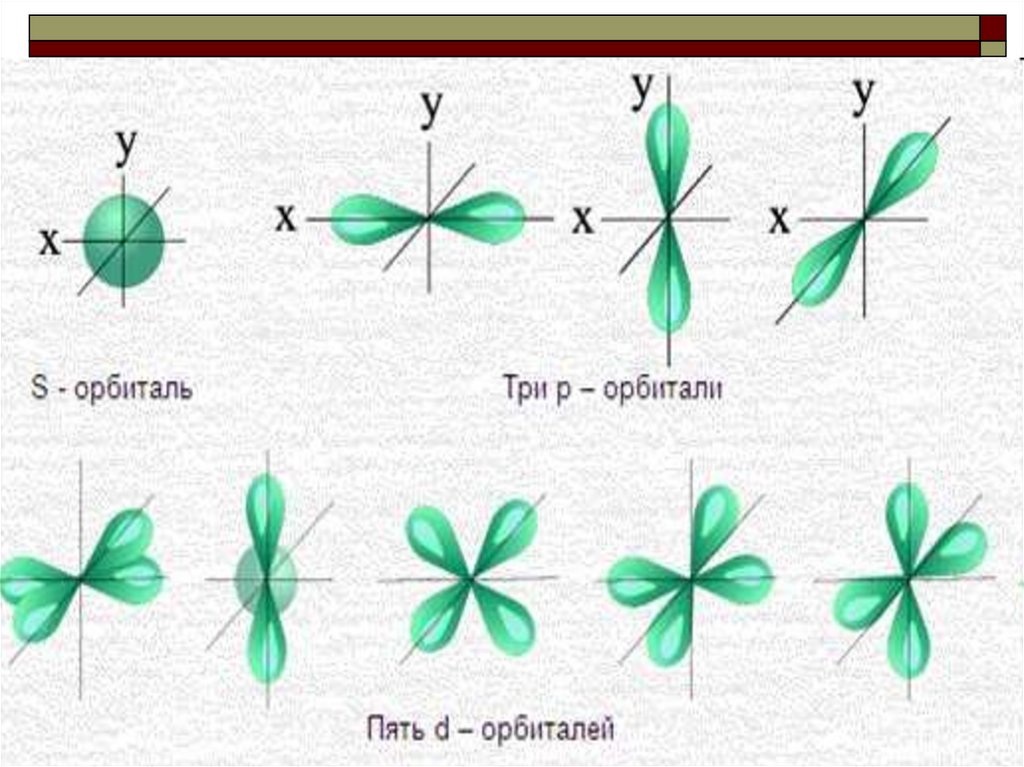
18.

Орбитали, или иначе электронные облака,
имеют разную геометрическую форму. Для
атомных орбиталей приняты обозначения:
s
(форма сферы), р (форма поверхности
гантели или восьмерки),
d и f (более сложные формы)

19.

20.

21.

22. Спин

Спин
(англ.
spin,
букв.-вращение),
собственный момент количества движения
элементарной частицы (электрона, протона
и т. п.).
Имеет квантовую природу и не связан с
какими-либо перемещениями частицы, в
том числе не зависит от наличия или
отсутствия у нее орбитального (углового)
момента количества движения.

23.

24. Спиновое квантовое число

Количество
электронов
на
орбитали
определяется четвертым квантовым числом
– спиновым (обозначается как s).
Это число отражает наличие у электрона
собственного углового момента (ранее
связывалось с вращением электрона вокруг воображаемой
оси по или против часовой стрелки).

25.

Спины электронов могут быть ориентированы в
направлениях, которые обычно называют "спинвверх"
(мажорные
спины)
и
"спин-вниз"
(минорные спины).

26.

Если поместить электроны в магнитное
поле, то их спины выстроятся вдоль
направления поля.
При этом они будут прецессировать
(определенным образом вращаться) вокруг
силовых линий - это явление можно
сравнить с орбитальной прецессией нашей
планеты.

27.

28. Спиновое квантовое число S

Спиновое (магнитное спиновое) квантовое
число ms. Оно может принимать только два
значения ( 1 )
2
и характеризует возможные значения
проекции на ось Z спина (собственного
механического момента) электрона
Llsz ms

29.

Абсолютная
величина
спинового
импульса электрона Lls находится по
формуле
Lls
где
s –
равное 1/2.
s( s 1)
спиновое квантовое число,

30. Свойства спина

В отличие от орбитального углового
момента,
который
порождается
движением частицы в пространстве,
спин не связан с движением в
пространстве.
Спин — это внутренняя, исключительно
квантовая
характеристика,
которую
нельзя
объяснить
в
рамках
релятивистской механики.

31.

Если электрон движется
по
часовой
стрелке
(рис.), то ток направлен
против часовой стрелки
и вектор рm
(в соответствии с правилом
правого винта) направлен
перпендикулярно
плоскости
орбиты
электрона, как указано
на рисунке.

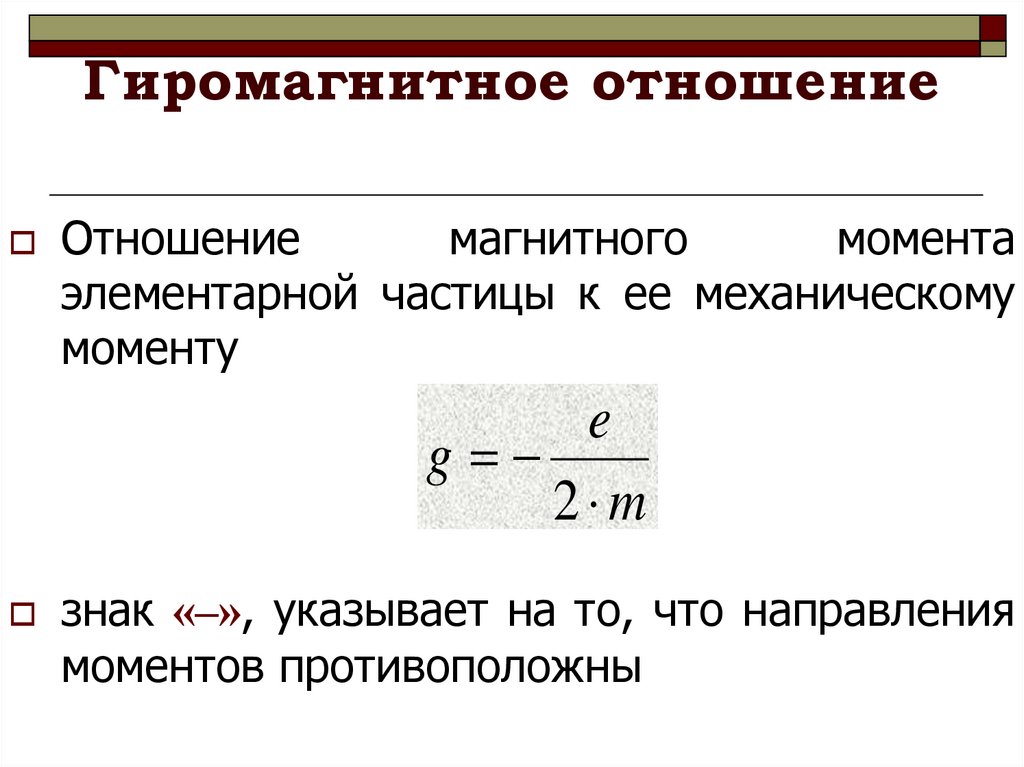
32. Гиромагнитное отношение

Отношение
магнитного
момента
элементарной частицы к ее механическому
моменту
e
g
2 m
знак «–», указывает на то, что направления
моментов противоположны

33. Магнетон Бора.

Магнетон Бора - квантовый магнитный
момент электрона.
Он является единицей магнитного
момента электрона. Данная величина
названа в честь Нильса Бора.
e
B
2 me

34.

В общем случае магнитный момент
электрона складывается из орбитального и
спинового магнитных моментов.
Магнитный момент
складывается из
входящих в его
магнитного момента
атома, следовательно,
магнитных моментов
состав электронов и
ядра
(обусловлен магнитными моментами входящих в
ядро протонов и нейтронов).

35. Вывод

Однако магнитные моменты ядер в тысячи раз меньше
магнитных
моментов
электронов,
поэтому
ими
пренебрегают.
Таким образом, общий магнитный момент
атома (молекулы) равен векторной сумме
магнитных моментов (орбитальных и
спиновых) входящих в атом (молекулу)
электронов

36. Принцип Паули

37. Принцип Паули (принцип исключения)

в одном и том же атоме (или в какой – либо
другой квантовой системе) не может быть
двух электронов, обладающих одинаковой
совокупностью четырех квантовых чисел:
главного n, орбитального l, магнитного m
и спинового ms. Иными словами, в одном
и том же состоянии не могут
находиться
одновременно
два
электрона.

38.

Для электронов в атоме принцип Паули
записывается следующим образом
Z1(n, l, m, ms) = 0 или 1,
где
Z1(n, l, m, ms ) – число электронов в
состоянии,
характеризуемом
данным
набором квантовых чисел.

39.

Максимальное число
Z2(n, l, m,)
электронов, находящихся в состояниях,
описываемых набором трех квантовых
чисел и отличающихся только ориентацией
спинов
Z2(n, l, m,) = 2,
так как спиновое квантовое число ms
может принимать лишь два значения 1/2 и
– 1/2.

40.

Максимальное число Z3(n, l) электронов,
находящихся в состояниях, определяемых
двумя квантовыми числами n и l
Z3(n, l) = 2(2l + 1).

41.

Максимальное число
Z(n) электронов,
находящихся в состояниях, определяемых
значением главного квантового числа n
Z ( n)
l n 1
l 0
Z 3 (n, l ) 2n
2

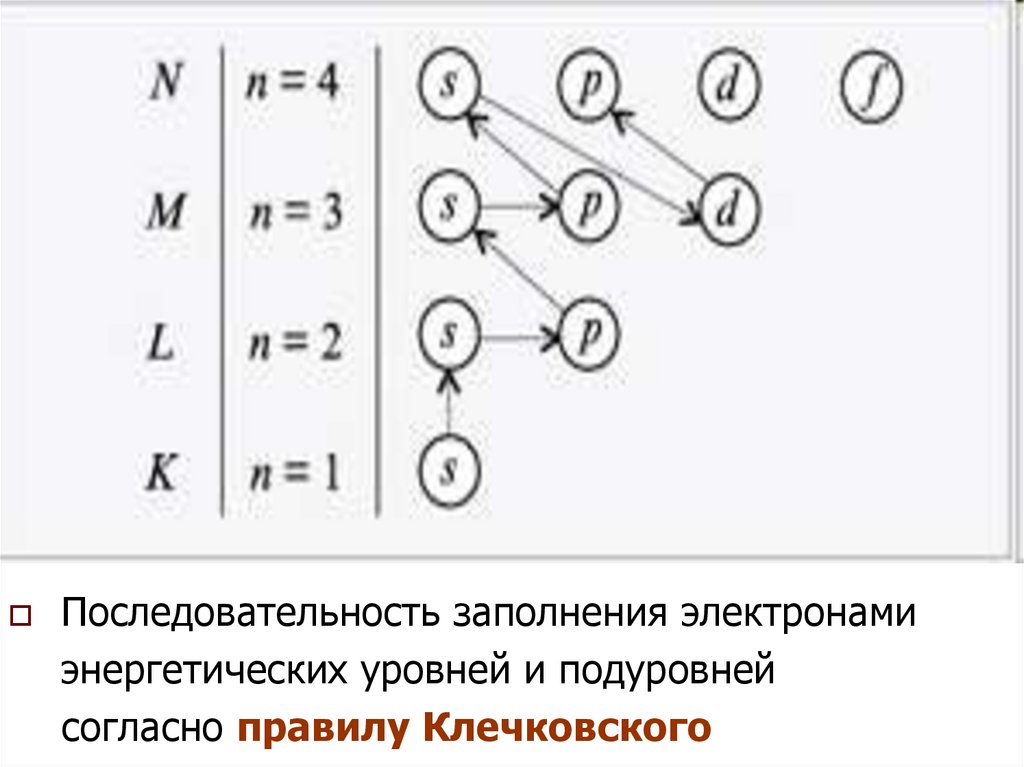
42.

43. Правило Клечковского

принцип наименьшей
энергии

44.

последовательность
заселения
электронами энергетических уровней и
подуровней в атоме должна отвечать
наибольшей связи электронов с ядром,
т.е.
электронная
система
должна обладать наименьшей
энергией.

45.

Порядок
заполнения
энергетических
состояний определяется стремлением
атома к минимальному значению суммы
главного и побочного квантовых чисел,
причем при фиксированном значении
(n
заполняются
+ l)
состояния,
минимальному значению
n.
отвечающие

46.

Последовательность заполнения электронами
энергетических уровней и подуровней
согласно правилу Клечковского

47. Правило Хунда

Электроны располагаются на орбиталях
таким образом, чтобы суммарный спин
атома был максимален.
Согласно этому правилу в пределах
энергетического подуровня все орбитали
сначала заселяются одним электроном, а
затем – вторым.

48. Правило отбора

49. Правило отбора

правила,
определяющие
возможные
квантовые переходы для атомов, молекул,
атомных
ядер,
взаимодействующих
элементарных частиц и др.
устанавливают, какие квантовые переходы
разрешены (вероятность перехода велика)
и какие запрещены — строго (вероятность
перехода равна нулю) или приближённо
(вероятность перехода мала)

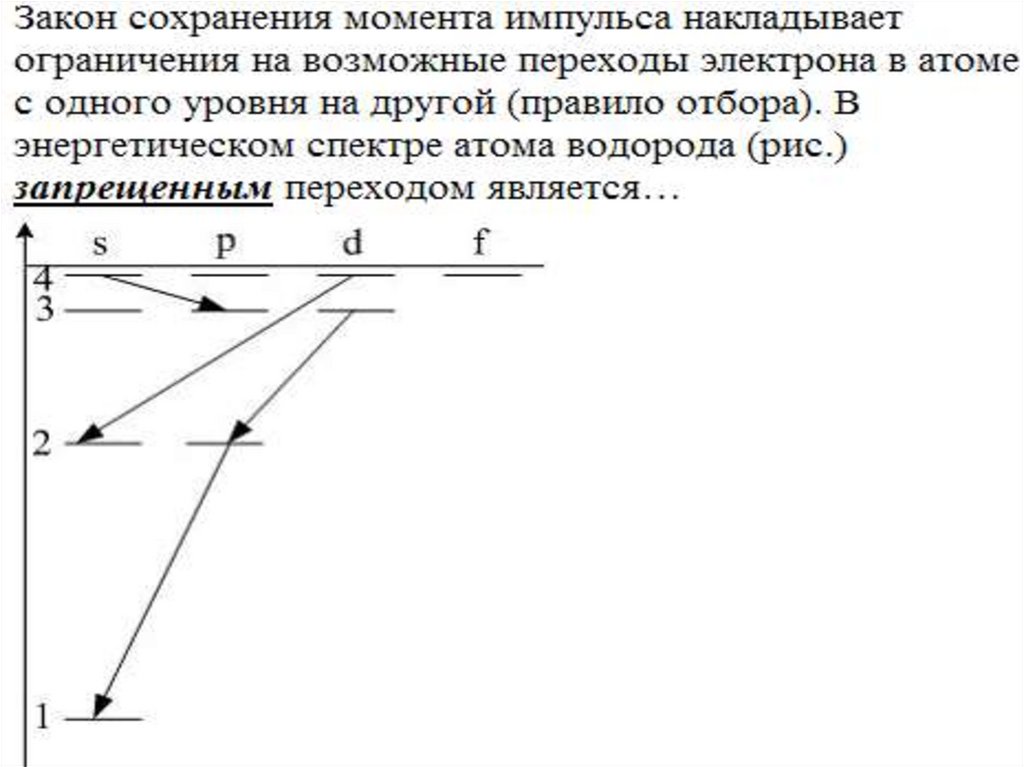
50. Правило отбора

Переходы с нарушением строгих законов
сохранения
(например,
энергии,
импульса,
момента количества движения, электрического
заряда и т.д. замкнутой системы) абсолютно
исключаются.
Если состояния системы характеризуются с
помощью квантовых чисел, то правила отбора
определяют их возможные изменения при
квантовых переходах рассматриваемого типа.

51. Магнитное квантовое число

Для магнитного квантового числа
свет, который испускается при переходе с
,
линейно
поляризован.
При
переходах с
испускается
циркулярно поляризованный свет.

52. Квантовое число полного момента

Для квантового числа полного момента
многоэлектронной системы
кроме того, запрещены переходы между
состояниями, в которых оба квантовых
числа полного момента равны нулю.

53. Орбитальное квантовое число

Для орбитального квантового числа

54.

55.

56.

57.

58. Физические основы применения рентгеновского излучения в медицине

59.

60.

61.

Рентгеноскопия грудной
клетки.

62.

Рентгенография

63.

64.

Легкие курильщика

65.

66. Компью́терная томогра́фия

Метод
неразрушающего
послойного
исследования
внутренней
структуры
объекта, был предложен в 1972 году
Годфри Хаунсфилдом и Алланом Кормаком,
удостоенными
за
эту
разработку
Нобелевской премии.
Метод основан на измерении и сложной
компьютерной
обработке
разности
ослабления
рентгеновского
излучения
различными по плотности тканями.