Оптические явления

1.

company name

2.

ОПТИКА
Оптика (от греч. optike - зрительный ) - раздел физики, изучающий
природу и свойства света, процессы его излучения и распространения,
взаимодействие света с веществом.
Природа света
корпускулярная
(Ньютон)
Свет – поток частиц
(квантов или фотонов)
company name
E h - энергия кванта (Планк)
волновая
(Гюйгенс)
Свет
–
совокупность
поперечных монохроматических
электромагнитных волн

3.

Геометрическая
оптика
Геометрическая
оптика
раздел
оптики,
изучающий
законы
распространения света в прозрачных средах, законы отражения света от
зеркальных поверхностей и принципы построения изображений при
прохождении света в оптических системах.
Световой луч – это линия, вдоль которой
распространяется энергия от источника света. В
однородной оптической среде световые лучи
представляют собой прямые линии (Евклид).
Законы геометрической оптики:
company name
1) закон прямолинейного распространения света – в
однородной среде свет распространяется прямолинейно.
оптически
Оптически однородной считается такая среда, в которой свет
распространяется с постоянной скоростью.
Среду, в которой свет распространяется с меньшей скоростью, называют
оптически более плотной.
Среду, в которой свет распространяется с большей скоростью, называют
оптически менее плотной.

4.

Законы
геометрической
оптики
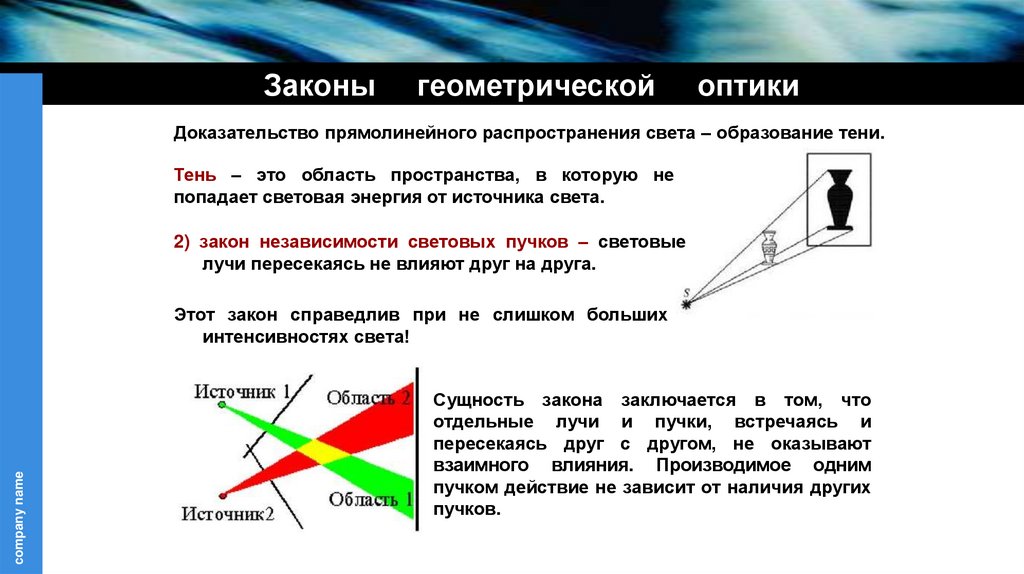
Доказательство прямолинейного распространения света – образование тени.
Тень – это область пространства, в которую не
попадает световая энергия от источника света.
2) закон независимости световых пучков – световые
лучи пересекаясь не влияют друг на друга.
company name
Этот закон справедлив при не слишком больших
интенсивностях света!
Сущность закона заключается в том, что
отдельные лучи и пучки, встречаясь и
пересекаясь друг с другом, не оказывают
взаимного влияния. Производимое одним
пучком действие не зависит от наличия других
пучков.

5.

Законы
геометрической
оптики
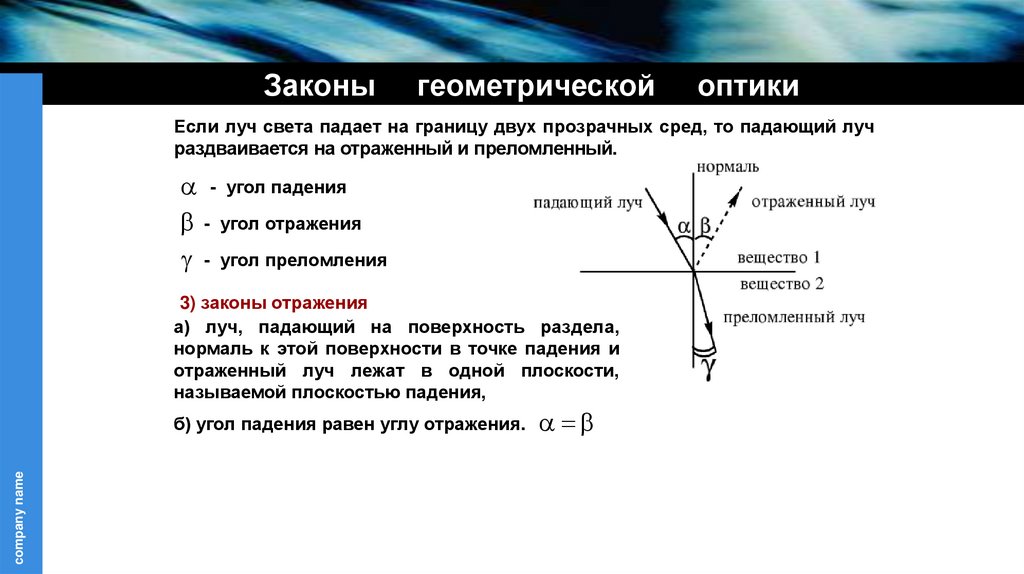
Если луч света падает на границу двух прозрачных сред, то падающий луч
раздваивается на отраженный и преломленный.
- угол падения
- угол отражения
- угол преломления
3) законы отражения
а) луч, падающий на поверхность раздела,
нормаль к этой поверхности в точке падения и
отраженный луч лежат в одной плоскости,
называемой плоскостью падения,
company name
б) угол падения равен углу отражения.

6.

Законы
геометрической
оптики
4) законы преломления
а) луч, падающий на поверхность раздела, нормаль к этой поверхности в точке падения и
преломленный луч лежат в одной плоскости,
б) закон Снеллиуса – отношение синусов угла падения и угла преломления есть величина постоянная
для двух данных сред, называемая относительным показателем преломления.
sin
n21
sin
n21 -
относительный
показатель
преломления
второй
среды
относительно первой.
n2
n21
n1
company name
n2 и n1 - абсолютные показатели преломления второй и первой сред.
Абсолютным показателем преломления вещества называется величина
n, равная отношению скорости света в вакууме к скорости света в данной
среде:
n c V

7.

Законы
Пусть в первой среде
геометрической
оптики
n1 c V1 , а во второй n2 c V2 , тогда
sin c V2 V1
Физический
смысл
относительного
n21 показателя преломления состоит в том, что
sin c V1 V2
он показывает, во сколько раз скорость
света в одной среде больше, чем в другой.
Если свет переходит из оптически менее плотной среды в оптически более
плотную ( n1 n2 ), например, из воздуха в стекло, то угол преломления
оказывается меньше угла падения, .
company name
Если свет переходит из оптически более плотной среды в оптически менее
плотную ( n1 n2 ), например, из стекла в воздух, то угол преломления
оказывается меньше угла падения, .
2

8.

Законы
геометрической
оптики
Угол падения, при котором угол преломления равен 2 , называется
предельным углом падения пр .
При углах падения пр свет полностью отражается от
границы раздела.
Явление, при котором луч света не переходит во
вторую среду, полностью отражаясь от границы
раздела, называется полным внутренним отражением.
Предельный угол можно определить из закона Снеллиуса:
если
пр , то 2 , следовательно
sin пр
company name
sin 2
sin пр n21
n2
пр arcsin
n1

9.

ИНТЕРФЕРЕНЦИЯ
СВЕТА
Интерференцией называется явление наложения волн, при котором происходит устойчивое во времени
их взаимное усиление в одних точках пространства и ослабление в других.
Впервые явление интерференции было обнаружено Робертом Бойлем (1627-1691 г.) и Робертом Гуком
(1635-1703 г.).
В 1801 г. Томас Юнг впервые объяснил явление интерференции света, ввел сам термин
«интерференция» и объяснил разноцветную окраску тонких пленок.
Необходимым условием интерференции волн является их когерентность, т.е. согласованное
протекание во времени и пространстве нескольких колебательных процессов.
Две волны называются когерентными, если разность их фаз не изменяется во времени.
Когерентными могут быть волны с одинаковой частотой.
Свет представляет собой электромагнитные волны.
E , H - векторы напряженности электрического и магнитного полей волны
E E 0 cos t kr
company name
H H 0 cos t kr
E 0 , H 0 - амплитуды векторов E , H
- круговая частота
Поскольку
основное
E
r - расстояние от источника
взаимодействие света с веществом
связано с вектором
, то его
k 2 - волновое число
принято
называть
световым
вектором.
t kr - фаза волны

10.

ИНТЕРФЕРЕНЦИЯ
условие максимума
Максимальная интенсивность
I I1 I 2 2 I 1 I 2
наблюдается при разности фаз
2 1 2m ; m 0,1,2...
company name
В
рассматриваемой
точке
колебания
происходят
с
одинаковыми
фазами
и
усиливают друг друга, амплитуда
колебаний точки максимальна и
равна удвоенной амплитуде.
СВЕТА
условие минимума
Минимальная интенсивность
I I1 I 2 2 I 1 I 2
наблюдается при разности фаз
2 1 2m 1 ; m 0,1,2...
Волны
приходят
в
рассматриваемую
точку
в
противофазе и гасят друг друга.
Амплитуда в точке наложения
волн равна нулю.
Если накладываются когерентные волны равной интенсивности I1 I 2 ,
то результирующая интенсивность принимает значения от I min 0 до
I max 4 I1 .

11.

ИНТЕРФЕРЕНЦИЯ
СВЕТА
Поскольку длина волны, а значит и волновое число k, зависит от
показателя преломления среды: 1 n1 , 2 n2
( - длина
волны в вакууме).
Тогда
2
2 1
r2n2 r1n1
Произведение геометрической длины пути r световой волны в данной
среде на показатель преломления n этой среды называется оптической
длиной пути L, а разность оптических длин проходимых волнами путей –
оптической разностью хода
r2 n2 r1n1 L2 L1
company name
Максимум и минимум интерференции наблюдается в том случае, если
оптическая разность хода равна
max m - условие максимума
min 2m 1
m 0, 1, 2...
2
- условие минимума
целое
число,
определяющее
порядок
интерференционного максимума или минимума.

12.

ОПТИКА
Интерференция света в тонких пленках
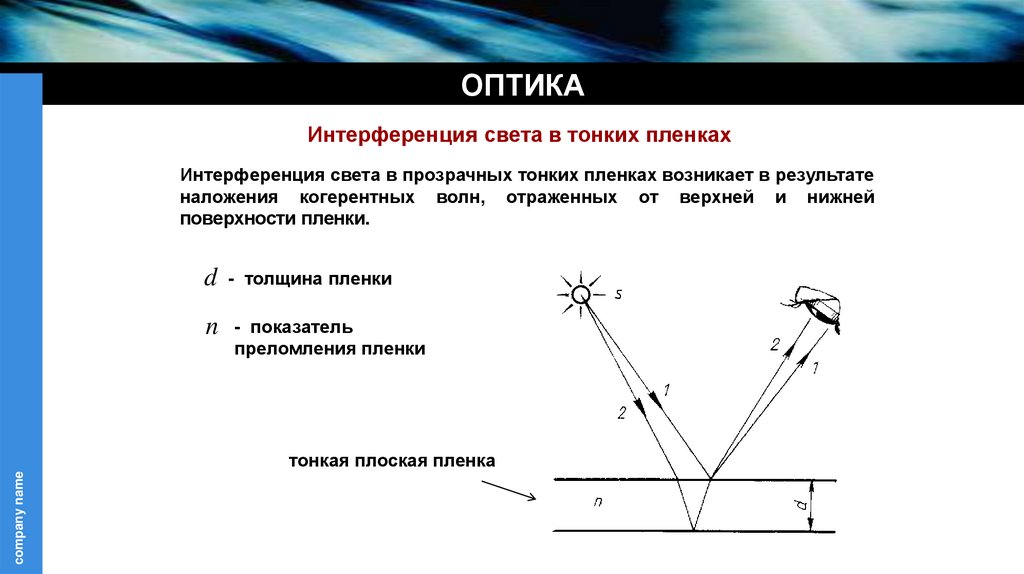
Интерференция света в прозрачных тонких пленках возникает в результате
наложения когерентных волн, отраженных от верхней и нижней
поверхности пленки.
d - толщина пленки
n - показатель
преломления пленки
company name
тонкая плоская пленка

13.

ОПТИКА
Интерференция света в тонких пленках
Интерференционная
картина
определяется оптической разностью
хода
между
интерферирующими
лучами.
L L2 L1 n AB BC AD
Согласно рисунку
company name
AB BC
h
cos
AD AC sin 2h tg sin
Учитывая закон преломления,
sin n sin

14.

Интерференция света в тонких пленках
получим
2dn
2dn
sin 2 2dn
2
2dn tg sin
2dn
1
sin
cos
cos
cos cos
2dn cos 2
2dn cos
cos
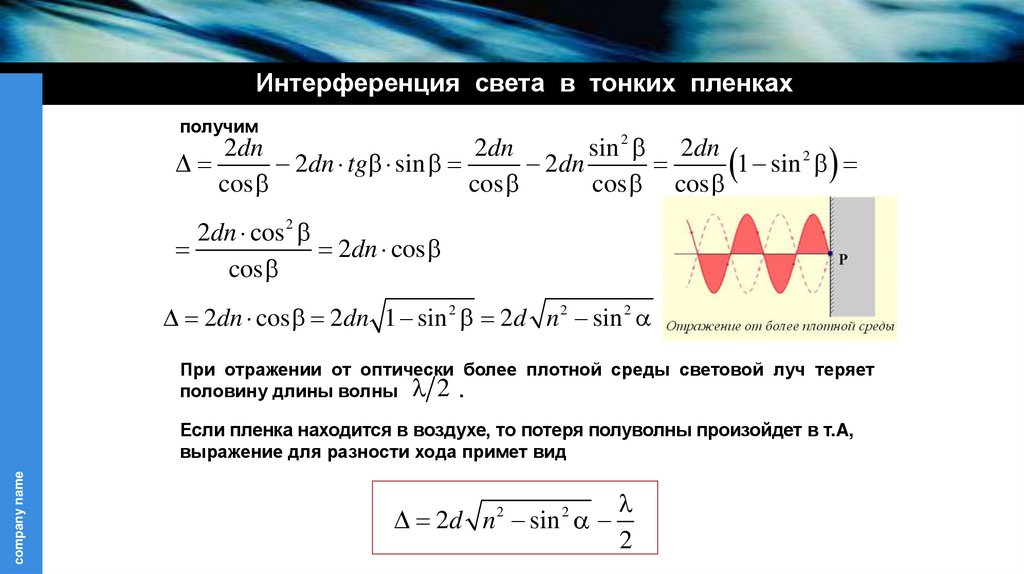
2dn cos 2dn 1 sin 2 2d n 2 sin 2
При отражении от оптически более плотной среды световой луч теряет
половину длины волны 2 .
company name
Если пленка находится в воздухе, то потеря полуволны произойдет в т.A,
выражение для разности хода примет вид
2d n 2 sin 2
2

15.

Интерференция света в тонких пленках
В точке P будет наблюдаться интерференционный максимум, если
выполняется условие
L m
2d n sin m
2
2
2
2d n sin 2m 1
2
2
2
В точке P будет наблюдаться интерференционный минимум, если
выполняется условие
company name
L 2m 1
2
2d n sin 2m 1
2
2
2
2d n 2 sin 2 m
2

16.

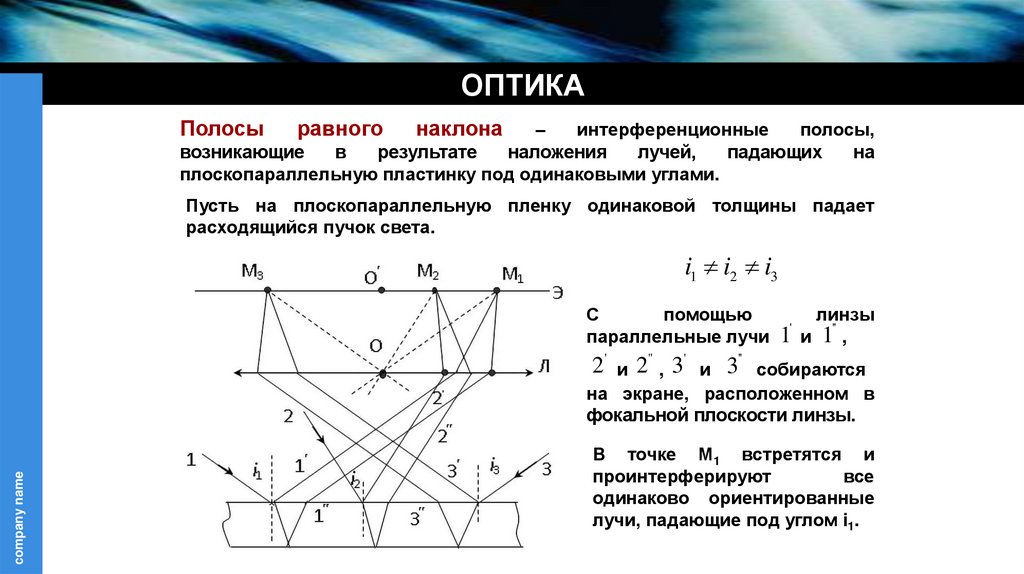
ОПТИКА
Полосы
равного
наклона
–
интерференционные
полосы,
возникающие
в
результате
наложения
лучей,
падающих
на
плоскопараллельную пластинку под одинаковыми углами.
Пусть на плоскопараллельную пленку одинаковой толщины падает
расходящийся пучок света.
i1 i2 i3
С
помощью
линзы
'
''
параллельные лучи 1 и 1 ,
2' и 2'' , 3' и 3'' собираются
company name
на экране, расположенном в
фокальной плоскости линзы.
В точке М1 встретятся и
проинтерферируют
все
одинаково ориентированные
лучи, падающие под углом i1.

17.

Полосы равного наклона
company name
Если рассмотреть луч 3 с тем же углом падения i1, но иначе ориентированный
по отношению к пластинке, то интерференция подобных ему лучей будет
наблюдаться в другой точке экрана, в т. М3, находящейся на таком же
расстоянии от центра экрана, что и точка М1. Таким образом, лучи с углом
падения i1, но с разными ориентациями, образуют на экране кольцо,
освещенность которого будет зависеть от разности хода лучей.
Лучи с углом падения i2 и всевозможных ориентаций образуют на экране
кольцо с тем же центром, но другого радиуса. В итоге на экране получится
интерференционная картина , состоящая из светлых и темных колец, каждое из
которых соответствует строго определенному углу наклона (углу падения)
лучей.

18.

Интерференция света
Полосы равной толщины
Параллельный пучок света падает на пленку переменной толщины (клин).
Интерференционные
полосы
будут наблюдаться там, где
толщина пленки удовлетворяет
условиям
максимума
или
минимума
max m min 2m 1
2
company name
Результат интерференции в точках P1 и P2 экрана определяется по
формуле, подставляя в нее толщину пленки в месте падения луча (b1 или
b2)
2b n 2 sin 2
2
Свет обязательно должен быть параллельным
const : если
одновременно будут изменяться два параметра b и , то устойчивой
интерференционной картины не будет.

19.

Полосы равной толщины
company name
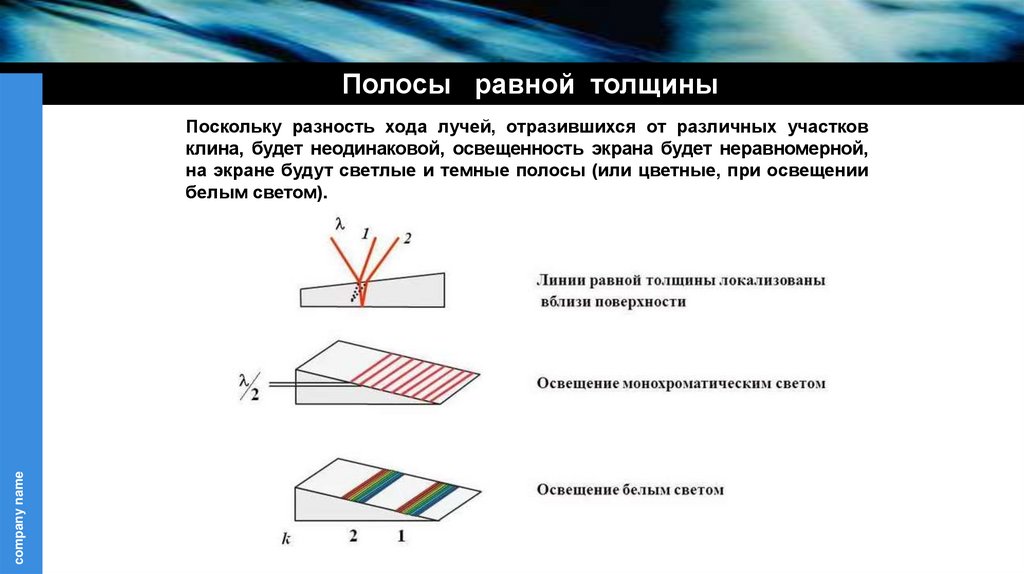
Поскольку разность хода лучей, отразившихся от различных участков
клина, будет неодинаковой, освещенность экрана будет неравномерной,
на экране будут светлые и темные полосы (или цветные, при освещении
белым светом).

20.

Полосы равной толщины
Кольца Ньютона – частный случай полос равной толщины.
Кольца Ньютона наблюдаются при отражении
света
от
верхней
и
нижней
границ
воздушного
зазора
между
плоскопараллельной
пластинкой
и
соприкасающейся с ней плосковыпуклой
линзой.
h - толщина воздушного зазора
company name
Параллельный пучок света падает на плоскую
поверхность линзы и частично отражается от
верхней и нижней поверхности воздушного
зазора между линзой и пластинкой.
При наложении отраженных лучей возникают
полосы равной толщины (концентрические
окружности).

21.

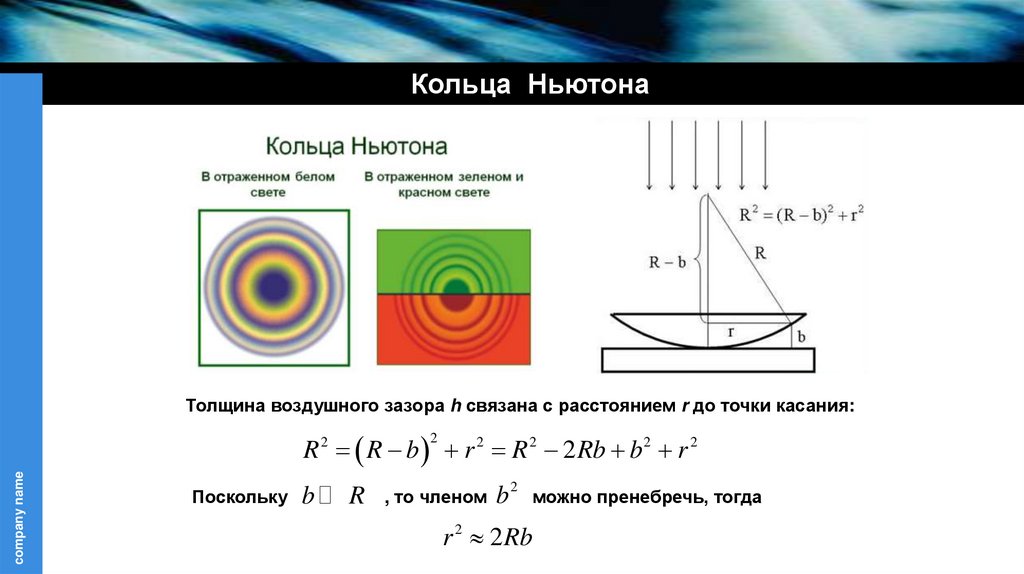
Кольца Ньютона
Толщина воздушного зазора h связана с расстоянием r до точки касания:
R R b r 2 R 2 2 Rb b 2 r 2
2
company name
2
Поскольку
b
R
, то членом b
2
можно пренебречь, тогда
r 2 2 Rb

22.

Кольца Ньютона в отраженном свете
Толщина зазора h определяет оптическую разность хода между лучами,
отраженными от верхней и нижней границы зазора между линзой и
пластинкой, которая с учетом потери полуволны на отражение равна:
2bn
2
, где
r
b
2R
Если выполняется условие
наблюдается светлое кольцо:
max m
company name
интерференционного
r2
n m
R
2
Если выполняется условие
наблюдается темное кольцо:
min 2m 1
2
r2
r2
2
n n
2R
2 R
2
2
максимума,
то
1
m
R
2
rmсв
n
интерференционного
r2
n 2m 1
R
2
2
минимума,
темн
m
r
то
m R
n

23.

Кольца Ньютона в проходящем свете
m 0,1,2.. - номер кольца
company name
В проходящем свете интерференционные максимумы
меняются местами:
и минимумы
Оптическая разность хода для проходящего и отраженного света
отличается на / 2 , т.е. максимумам интерференции в отраженном свете
соответствуют минимумы в проходящем, и наоборот.
Светлым кольцам в отраженном свете будут соответствовать темные
кольца в проходящем.

24.

Дифракция света
company name
Типы дифракции
Принцип Гюйгенса-Френеля
Зоны Френеля

25.

Дифракция света
company name
(лат. diffractus – «огибание препятствия волнами»)
Дифракция света – совокупность явлений, связанных с отклонениями от
законов геометрической оптики и наблюдаемых при распространении
света в среде с резкими неоднородностями.
Дифракция света - отклонение света от прямолинейного направления
распространения при прохождении вблизи препятствий, т.е. свет огибает
препятствия.
Дифракция света приводит к огибанию световыми волнами
препятствий и проникновению света в область геометрической тени.

26.

Дифракция света
Дифракционные картины от различных препятствий
1) Если на пути параллельного светового пучка расположено круглое
препятствие (круглый диск, шарик или круглое отверстие в непрозрачном
экране), то на экране, расположенном на достаточно большом расстоянии
от препятствия, появляется дифракционная картина система
чередующихся светлых и темных колец.
company name
2) Если препятствие имеет линейный характер (щель, нить (игла), край
экрана), то на экране возникает система параллельных дифракционных
полос.

27.

Дифракция света Принцип Гюйгенса
Принцип Гюйгенса – каждая точка, до которой доходит волна,
служит центром вторичных сферических волн, а огибающая этих
волн задает положение волнового фронта в следующий момент
времени.
На плоскую преграду с отверстием падает параллельный фронт
волны. Согласно Гюйгенсу любая точка выделяемого отверстием
участка волнового фронта служит центром вторичных волн,
которые в однородной изотропной среде будут сферическими.
company name
Принцип Гюйгенса решает задачу о направлении распространении
волнового фронта, но не затрагивает вопроса об амплитуде, а,
следовательно, и об интенсивности волн, распространяющихся по
различным направлениям. Этот недостаток был устранен
Френелем.
Принцип Гюйгенса-Френеля: каждая точка волновой поверхности служит
источником вторичных сферических волн. Все вторичные источники,
расположенные на одной и той же волновой поверхности, когерентны
между собой. Результирующая волна в произвольной точке пространства
является результатом интерференции вторичных волн.

28.

Принцип Гюйгенса - Френеля
Метод зон Френеля
Френель предложил разбить волновую поверхность на кольцевые зоны такого размера, чтобы
расстояния от краев соседних зон до точки наблюдения отличались на половину длины волны.
Зоны Френеля – сферические сегменты на волновой поверхности.
Расстояния от краев зон до точки M изменяется на λ/2.
A1 , A2 ... A n - амплитуда волны, пришедшей в точку M от
i-ой зоны Френеля
A1 A2 A 3 A4 ...
company name
Амплитуды колебаний Ai монотонно убывают, т.к. с увеличением номера
зоны i:
1) увеличивается расстояние l ,
2) увеличивается угол α между нормалью к зоне и направлением на точку
наблюдения,
3) площади зон остаются приблизительно одинаковыми.

29.

Метод зон Френеля
Амплитуды колебаний Ai монотонно убывают:
Am 1 Am 1
Am
2
A1 A2 A 3 A4 ...
Результирующая амплитуда колебаний в точке M равна:
Aрез Ai A1 A2 A3 A4 A5 ...
0
0
0
company name
A1 A1
A3 A3
A5 A5
A7
Aрез A2 A4 A6 ...
2 2
2 2
2 2
2
Aрез
A1
2
Амплитуда результирующего колебания в точке M равна половине
амплитуды колебаний от первой зоны Френеля.