Конвективный теплообмен

1.

КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

2. Конвективный теплообмен

Конвективный теплообмен - процесс передачи теплоты при
движении жидкости или газа, осуществляемый при
совместным действии конвекции и теплопроводности.
Конвекцией называется перенос макрочастиц (потоков)
жидкости в пространстве. Если эти частицы перемешаются из
области с одной температурой в область с другой
температурой, их перемещение сопровождается переносом
энергии. Перенос энергии конвекцией сопровождается
теплопроводностью при непосредственном соприкосновении
различно нагретых частиц жидкости.
Количество теплоты, отдаваемое жидкостью твердой стенке
или воспринимаемое жидкостью от стенки в единицу времени,
определяется уравнением Ньютона – Рихмана
Q t с t ж F
а плотность теплового потока
q t с t ж t

3.

Коэффициент теплоотдачи (α ), Вт/(м2·К) характеризует
интенсивность конвективного теплообмена между жидкостью
(газом) и поверхностью твердого тела; t
– температурный
напор, t tс t ж , K.
Коэффициент теплоотдачи (α ) определяет количество
теплоты, которое передается в единицу времени через 1 м2
поверхности тела при разности температур поверхности тела и
окружающей среды, равной 1 градусу
или коэффициент
теплоотдачи численно равен плотности теплового потока (q) при
температурном напоре, равном единице
t tс t ж .1
Коэффициент теплоотдачи зависит от многих факторов, и в
общем случае является функцией формы и размера тела,
режима движения жидкости (газа), физических свойств
жидкости (газа), положения в пространстве и состояния
поверхности теплообмена и других величин.
Процесс теплоотдачи в зависимости от природы движения
жидкости протекает различно. Различают вынужденную и
свободную конвекцию.

4.

При вынужденной конвекции жидкость или газ движутся за счет
внешних для данного процесса сил (насос, вентилятор, ветер), при
свободной конвекции – за счет разности плотностей нагретых и
холодных частиц жидкости. Свободное движение может
появиться в жидкости (газе) с переменной плотностью только в
том случае, когда жидкость находится в поле сил гравитации.
Вынужденное
движение
в
общем
случае
может,
сопровождается свободным движением. При больших скоростях
вынужденного движения, влияние свободной конвекции
становится пренебрежимо малым.
Изучение процесса теплоотдачи практически сводится к
определению зависимости коэффициента теплоотдачи
от
различных факторов.
В дальнейшем будут рассмотрены только стационарные
процессы теплоотдачи. Условием стационарности является
неизменность во времени скорости и температуры в любой точке
жидкости.

5. Дифференциальные уравнения конвективного теплообмена (факультатив)

Дифференциальное уравнение теплоотдачи получено при
условии
соблюдения
равенства
тепловых
потоков,
передаваемых конвективным теплообменом от газа к стенке
тела и теплопроводностью в пограничном слое газа
t
t c t ж n ж
Дифференциальное уравнение энергии при условии
однородности и несжимаемости жидкости, отсутствия
внутренних источников теплоты и работы расширения, а также
постоянства физических параметров жидкости в пределах
элементарного объема, формулируется следующим образом:
Dt
a 2t
d

6.

субстанциальная (полная) производная
Dt t
t
t
t
wx wy wz
d
x
y
z
локальное изменение температуры во времени в какойлибо точке жидкости характеризуется t
изменение температуры при переходе от точки к точке за
счет конвективного теплообмена характеризуется
t
t
t
wx wy wz
x
y
z
Дифференциальное уравнение неразрывности получается на
основе закона сохранения массы, и для сжимаемой жидкости
(газа) имеет следующий вид:
w x w y w z
0
x
y
z

7.

Уравнение движения (уравнение Навье-Стокса) в векторной
форме можно представить в следующем виде
Dw
2
g p w
d
Полученная
система
дифференциальных
уравнений
конвективного
теплообмена
описывает
бесконечное
множество конкретных процессов.
Точные решения этой системы имеются только для отдельных
частных случаев при ряде упрощающих предпосылок.
В связи с ограниченными возможностями аналитического
решения
системы
дифференциальных
уравнений
конвективного
теплообмена,
решающее
значение
приобретает эксперимент.
Цель экспериментального исследования заключается в
получении на основе опытных данных эмпирических
уравнений, по которым можно затем вести расчет
конвективного теплообмена в подобных процессах.

8. Основы теории подобия и метода анализа размерностей

Теория подобия применяется в том случае, если известны
дифференциальные уравнения, описывающие рассматриваемый процесс, но решить эти уравнения в общем виде
невозможно.
Теория подобия дает возможность из этих дифференциальных уравнений получить выражения безразмерных комп-лексов
(чисел или критериев подобия).
Теория подобия показывает, что решение системы дифференциальных уравнений может быть представлено в виде
функциональной связи чисел подобия, существенно сократив
количество переменных.
К
примеру,
вместо
зависимости
по
определению
коэффициента теплоотдачи
f l , w, , , , с р , t , , g ,
использовать уравнение подобия конвективного теплообмена
Nu f Re, Pr,Gr .

9.

Основные теоремы теории подобия
Два или несколько явлений будут подобны, если
подобны все физические величины, характеризующие
эти явления, т.е. подобные между собою явления
имеют одинаковые безразмерные комплексы критерии подобия.
Решение
дифференциального
уравнения,
описывающего данный процесс,
может быть
представлено в виде функциональной зависимости
между критериями подобия, характеризующими этот
процесс и полученными из исходного уравнения и
условий однозначности.
Подобны между собой те явления, которые
принадлежат к одному классу, к одному роду и имеют
равные определяющие критерии подобия.

10.

Условия подобия физических явлений:
подобные процессы протекают в геометрически
подобных системах;
для подобных физических явлений одноименные
величины (характеристики) в сходственных точках
пространства должны быть пропорциональны;
подобные физические явления должны относится к
одному классу;
подобные
физические
явления
описываются
одинаковыми дифференциальными уравнениями;
условия однозначности подобных явлений должны быть
одинаковыми, но могут отличаться численными
значениями;
для подобных физических явлений одноименные числа
подобия должны иметь одинаковые численные
значения.

11.

Моделирование – это экспериментальное изучение
физических явлений в лабораторных условиях на моделях
при отсутствии возможности проведения изучения явлений
в реальных натурных условиях на промышленном
объекте.
Целью
моделирования
является
создание
экспериментальных
установок
(моделей),
проведение на них экспериментальных исследований
и обработка экспериментальных данных для
получения численных значений коэффициентов в
уравнениях подобия. К примеру постоянных C, m, n, j в
уравнении подобия конвективного теплообмена
Nu C Re m Pr n Gr j .
Искомая величина - коэффициент теплоотдачи ( )
входит в определяемый критерий – критерий Нуссельта.
Остальные критерии – определяющие Re, Pr,Gr .

12.

Числа подобия
• Критерий Нуссельта характеризует соотношение
тепловых потоков, передаваемых за счет конвективного
теплообмена и теплопроводности, и является искомой
величиной
l
Nu
• Критерий Рейнольдса характеризует соотношение
между силами инерции и молекулярного трения
(вязкости)
w l
Re
• Критерий
Прандтля
характеризует
физические
свойства жидкости и их влияние на конвективный
теплообмен
cp
cp
Pr
a

13.

Числа подобия
• Критерий Грасгофа характеризует соотношение подъемной
силы, возникшей вследствие разности плотностей неравномерно
нагретых объемов жидкости и силы молекулярного трения, и
является параметром интенсивности свободного движения
жидкости
3
Gr
g t l
2
.
• Критерий Пекле определяется следующим образом:
Pe
w l
a
Re Pr
Для стационарного конвективного теплообмена
подобия (критериальное уравнение) принимает вид
уравнение
Nu f Re, Pr,Gr .
Поскольку критериальные уравнения получены на основе
обработки экспериментальных данных, то в каждом случае
указывается:
диапазон
характеристик,
при
которых
рекомендуется использовать предлагаемое уравнение;
определяющие температура и линейный размер.

14. Обработка и обобщение результатов эксперимента

Уравнение подобия конвективного теплообмена в
условиях вынужденного движения жидкости имеет
следующий вид
Nu f Re, Pr
На основе экспериментальных данных определяются
необходимые характеристики и рассчитываются значения
критериев подобия. Предположим, что зависимость между
критериями подобия имеет степенной вид, т.е.
Nu c Re Pr ,
n
m
где c, n, m – безразмерные постоянные величины.
Логарифмируя соотношение, получаем
lg Nu lg c n lg Re m lg Pr .
Наносим опытные значения критериев подобия во всем
диапазоне проведенных исследований на график.

15.

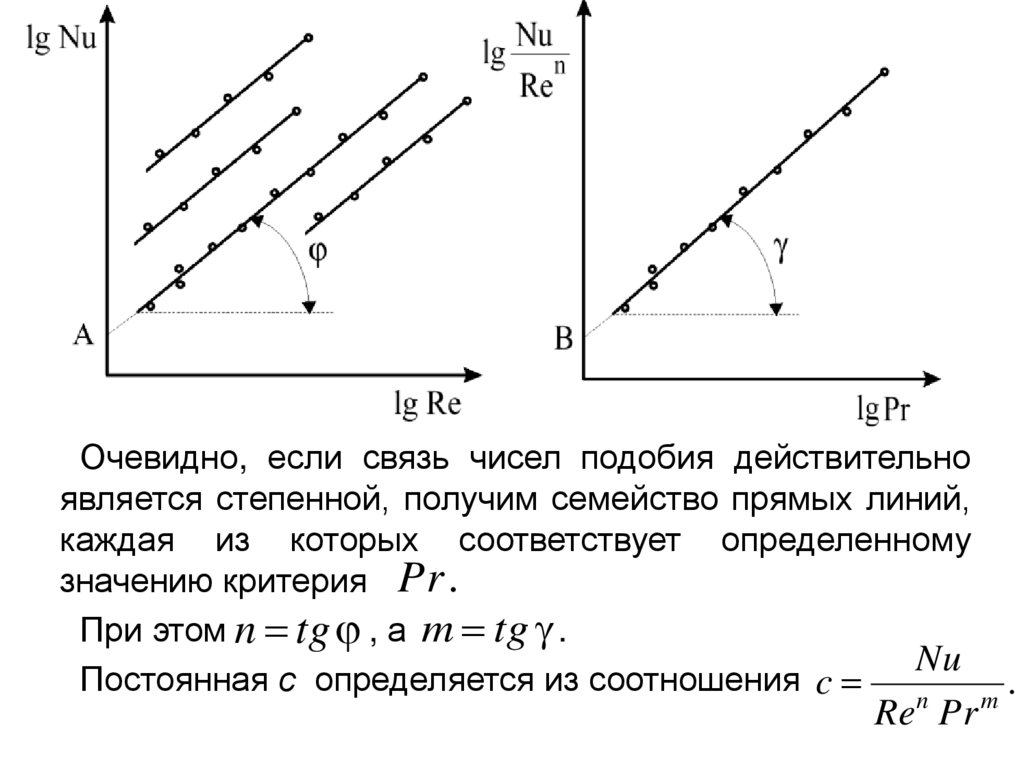
Очевидно, если связь чисел подобия действительно
является степенной, получим семейство прямых линий,
каждая из которых соответствует определенному
значению критерия Pr .
При этом n tg , а m tg .
Nu
Постоянная с определяется из соотношения c
.
n
m
Re Pr

16.

Спасибо за внимание !