Similar presentations:
Конвективный теплообмен в однофазных средах
1.
КОНВЕКТИВНЫЙТЕПЛООБМЕН В
ОДНОФАЗНЫХ СРЕДАХ
1
2. Конвективный тепломассообмен
Виды конвекцииВынужденная конвекция - движение жидкости
вызывается внешними силами (насос, вентилятор и др.)
Свободная (естественная) конвекция - движение
возникает под действием неоднородного поля
массовых сил (сила тяжести, центробежная сила и др.)
В рамках феноменологического метода среда
рассматривается как непрерывное вещество без
какой либо структуры.
Перенос тепла и массы происходит:
не только за счет grad T или grad C,
но и совместно с движущейся средой.
2
3.
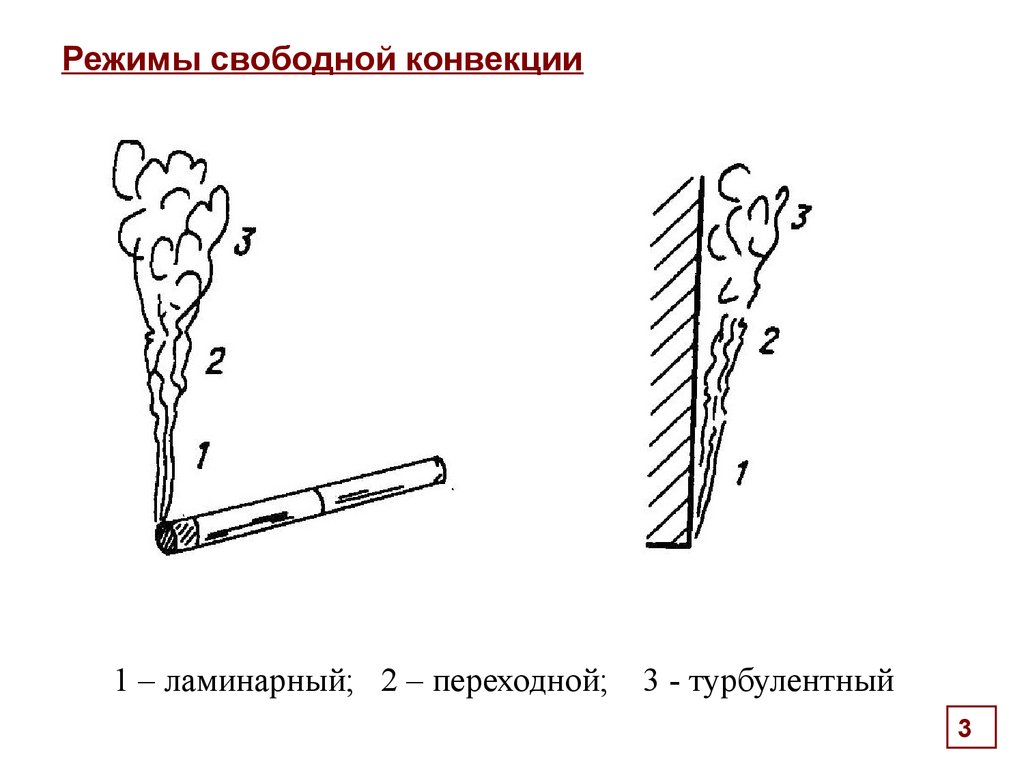
Режимы свободной конвекции1 – ламинарный; 2 – переходной;
3 - турбулентный
3
4. Осборн Рейнольдс Osborne Reynolds (1842-1912)
45.
Людвиг ПрандтльLudwig Prandtl
(1875-1953)
5
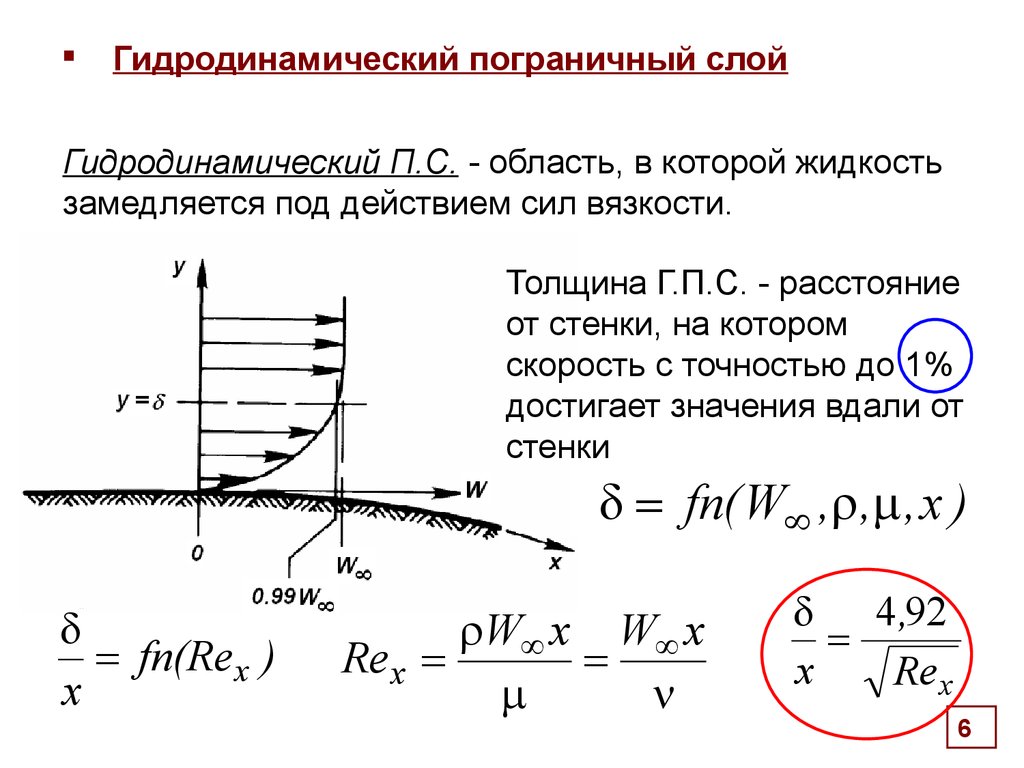
6. Гидродинамический пограничный слой
Гидродинамический П.С. - область, в которой жидкостьзамедляется под действием сил вязкости.
Толщина Г.П.С. - расстояние
от стенки, на котором
скорость с точностью до 1%
достигает значения вдали от
стенки
fn( W , , , x )
fn(Rex )
x
W x W x
Rex
4 ,92
x
Rex
6
7.
Гидродинамический пограничный слойЛаминарный поток
Турбулентный поток
ламинарный П.С.
переходной П.С.
развитый
турбулентный П.С.
вязкий
подслой
безразмерное расстояние
7
8. Тепловой пограничный слой
Тепловой или диффузионный П.С. - область вблизистенки, на которую
основная доля изменения
температуры
Г.У. III рода
t
f
( t w t )
y y 0
Закон Фурье
q_тепл
Число Нуссельта (Nusselt)
Tw T
Tw T
y
L y
Закон Ньютона
q_конв
L
L
Nu L
f
0
8
9. Ernst Kraft Wilhelm Nusselt (1882-1957)
910. Оценка толщины пограничного слоя
Касательное напряжение (Закон Ньютона)Оцениваем толщину П.С. из условия
Сила инерции единичного
объема жидкости в П.С.
Fин
dW
к
dy
Fин ~ Fm р
dW
dx dW
dW
W
d
d dx
dx
длина пластины L - порядок градиента скорости W/L
Сила трения, отнесенная к единице объема:
Fm р
d w
d 2W
W
2 ~ 2
1 1 dy
dy
L W L W
Fин
W2
~
L
W2
W
2
L
более точно
4 ,92
L
Re
10
11. Дифференциальные уравнения конвективного теплообмена (законы сохранения)
Dt2
a t
d
(1) энергии
DW 1
2
g
gradP
W
(2,3,4) количества движения
d
(5) массы
div( W ) 0
(6) состояния
(неразрывности)
F ( P ,V ,t ) 0
для газов
PV RT
Система из шести уравнений - шесть неизвестных
Wx ,W y ,Wz , P ,V ,t
11
12. Дифференциальные уравнения конвективного теплообмена
Субстанциональная производнаяD
Wx
Wy
Wz
(W grad )
x
y
z
условия однозначности :
геометрические (форма, размер);
физические (свойства);
временные (условия протекания процесса во времени);
граничные (скорости, температуры на границах и т.д.);
I, II, III рода
Все уравнения должны решаться совместно
12
13. Осреднение скорости по сечению канала
Через кольцо радиуса r,шириной dr протекает
количество жидкости
W ( r ) 2 r dr
Массовый расход
жидкости в трубе
Если const
R
G W R 2 W (r ) 2 r dr
W 2
R
R
2
W ( r ) r dr
0
Вводим безразмерные координаты,
r R
u W( r ) W
0
1
1
u
d
0
2
служит для проверки правильности измерений распределения скорости.
13
14. Осреднение температуры по сечению канала
Количество тепла в потоке жидкости:R
Q c p W t R 2 c p t( r ) W ( r ) 2 r dr
0
Если , c p const
средняя по теплосодержанию температура жидкости
R
1
W( r ) r r
t t( r )
2 d 2 t ( ) u( ) d
W
R R
0
0
.
14
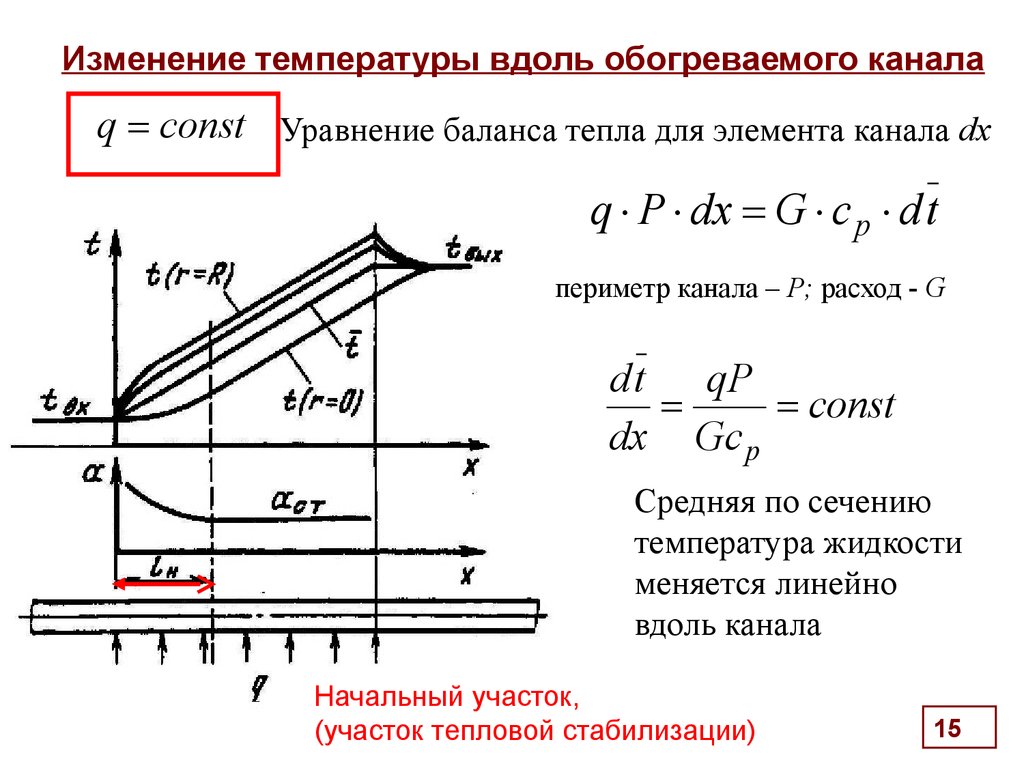
15. Изменение температуры вдоль обогреваемого канала
q const Уравнение баланса тепла для элемента канала dxq P dx G c p d t
периметр канала – P; расход - G
d t qP
const
dx Gc p
Средняя по сечению
температура жидкости
меняется линейно
вдоль канала
Начальный участок,
(участок тепловой стабилизации)
15
16. Изменение температуры вдоль обогреваемого канала
t w const , т.е. тепловой поток меняется по длине каналаУравнение теплового баланса:
Здесь
q( x) ( x) t w t f ( x)
q( x) P dx G c p d t
пусть температура стенки tw=0
( x) P
dt
dx
Gc p
t
После интегрирования
x ( x) P
t ( x) tвх exp
dx
0 Gc p
tвх – темп. жидкости на входе в канал
Начальный участок
16
17. Подобие и моделирование тепловых процессов
Данные, полученные при изучении одного явления, можнораспространить на другие явления, подобные данному
Условия подобия физических процессов (теорема Кирпичева-Гухмана):
1. Подобные процессы должны иметь одинаковую физическую
природу или описываться одинаковыми по форме
дифференциальными уравнениями.
Теплопроводность - электропроводность
2. Условия однозначности должны быть одинаковыми. Они
могут различаться лишь числовыми значениями.
Г.У.одного рода
3. Определяющие числа подобия (т.е. критерии подобия,
составленные из параметров, входящих в условия
однозначности) должны иметь одинаковые числовые значения.
Reнат = Reмод
17
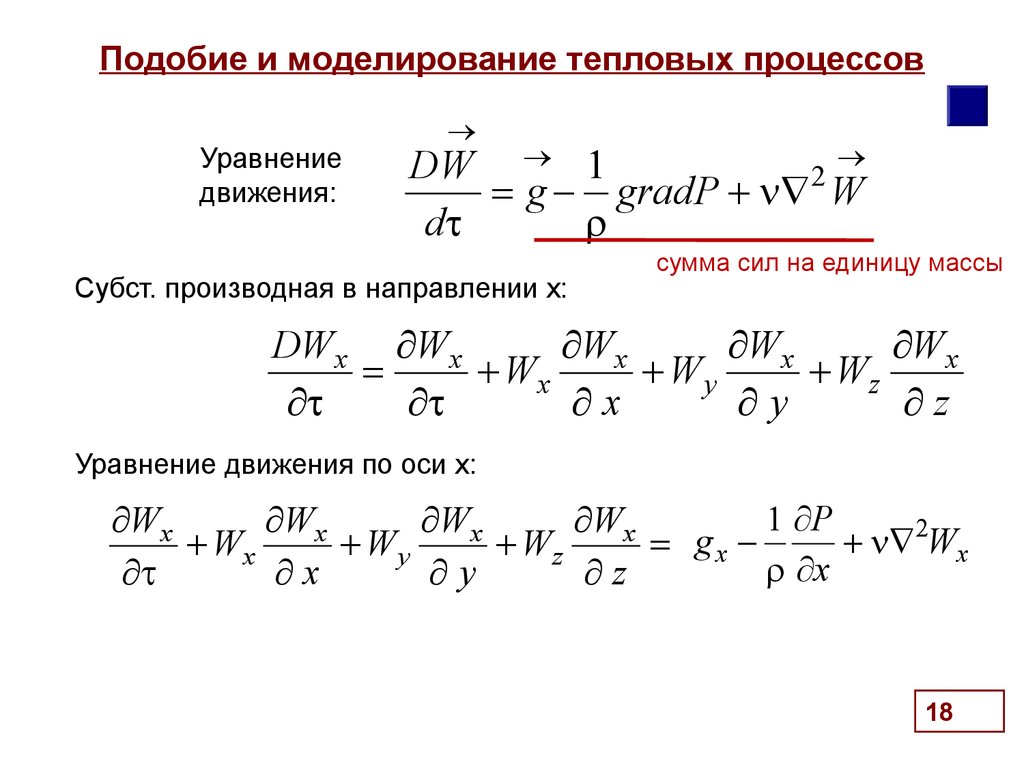
18. Подобие и моделирование тепловых процессов
Уравнениедвижения:
DW 1
2
g gradP W
d
Субст. производная в направлении х:
сумма сил на единицу массы
DWx Wx
Wx
Wx
Wx
Wx
Wy
Wz
x
y
z
Уравнение движения по оси х:
1 P
Wx
Wx
Wx
Wx
2Wx
Wx
Wy
Wz
gx
x
x
y
z
18
19. Подобие и моделирование тепловых процессов
Число Рейнольдса - характеристика отношения (но не самоотношение) инерционных сил к силам трения.
Fин
одномерное уравнение движения:
Введем безразмерные координаты:
x l
u Wx W
отношение сил инерции к
силам вязкости
Fвяз
Wx
2Wx
Wx
2
x
x
2
du
1 d u
Wu
d
l d 2
du
du
du
dWx
W u
u
u
Wx
d
d W l
d
dx
Re
2
2
2
2
d
u
1 d u
d u
d Wx
2
2
2
2
d
l d
d
dx
19
20. Подобие и моделирование тепловых процессов
Толкование числа Рейнольдса, данное КарманомСогласно кинетической теории кинематическая вязкость
с точностью до постоянного множителя равна сL, где с - средняя
скорость молекул; L - средняя длина свободного пробега.
W l
Re
c L
Т.е. с точностью до постоянного множителя :
В обычных задачах гидродинамики
l
L
W
c
W
Если
c не мало, как обычно, то нужен учет сжимаемости газа
l
Если
мало, то газ нельзя рассматривать как сплошную среду
L
20
21. Подобие и моделирование тепловых процессов
Физический смысл числа Нуссельтаа).
Пусть у стенки имеется неподвижный слой жидкости с
теплопроводностью , в котором сосредоточен весь
температурный напор. По этому напору рассчитывается
коэффициент теплообмена .
характерная длина
l
l
Nu
f
f /
толщина П .С .
Пример:
Теплообмен в трубе
Nu=100,
диаметр трубы в 100 раз больше толщины т.п.с.(где
сосредоточен почти весь температурный перепад ).
d
Nu
f
21
22. Подобие и моделирование тепловых процессов
б). Nu как характеристика отношения действительного тепловогопотока, определяемого коэффициентом теплообмена , и теплового
потока через слой l с теплопроводностью :
Nu
/l
в). Nu - безразмерный градиент
температуры на границе стенка-жидкость
q
t n n
q
tw t f
tw t
t
t
q
tw t f
n n
n n
Nu
tw t f q / l tw t f / l
n l
n
тангенс угла
наклона
касательной к
температурной
кривой у стенки
22
23. Подобие и моделирование тепловых процессов
теорема Букингема"Если какое-либо уравнение однородно относительно
размерностей (т.е. математическая запись не зависит
от выбора единиц), то его можно преобразовать к
соотношению, содержащему безразмерные
комплексы, составленные из определяющих
параметров".
Если не удается получить систему безразмерных величин,
описывающих какое-либо явление, то это верный признак
того, что было что-то пропущено.
23
24. Подобие и моделирование тепловых процессов
-теорема"Если существует однозначное соотношение между n
размерными физическими величинами
f1 A1 , A2 ,.....An
и эти переменные описываются при помощи k основных
единиц размерности, то исходное выражение эквивалентно
выражению
0
f 2 1 , 2 ,..... n k 0
где - безразмерные комплексы
т.е. если имеется n величин и k единиц, то можно получить
(n - k) безразмерных комбинаций".
24
25. Подобие и моделирование тепловых процессов
Пример : формула Дарси для расчета гидравлическогосопротивления канала:
- коэффициент гидравлического
l W 2
p
d 2
сопротивления трения;
l - длина;
d - гидравлический диаметр.
Из физических соображений
p f1 l , d , W , , ,
шероховатость
25
26. Подобие и моделирование тепловых процессов
Основные единицы для параметров функции f1масса (M), длина (L), время (T).
р
l
d
W
ML-1T-2
L
L
LT-1
ML-1T-1
ML-3
L
Предположим, что функция f1
степенная:
p l d W
a
b
c
d
e
f
Подставим размерности каждой величины:
ML 1T 2 La Lb ( LT 1 ) c ( ML 1T 1 ) d ( ML 3 ) e Lf
26
27. Подобие и моделирование тепловых процессов
Чтобы уравнение не зависело от выбора фундаментальных единиц(M,L,T), размерности в правой и левой частях должны быть равны:
M 1 d e
L 1 a b c d 3e f
T 2 c d
три уравнения,
шесть неизвестных
e=1-d; c=2-d; b=a-d-f
После подстановки:
p l d
a
a d f
W
2 d
d
1 d
f
Объединяем члены с одинаковыми показателями
d
a
p
l Wd
f
2
2
W
d
d
f
n=7
k=3
=7-3=4
27
28. Общие рекомендации перед началом эксперимента
Для определения безразмерных комбинаций, необходимых приобработке экспериментальных данных:
1. Выбрать независимые переменные, учесть различные
коэффициенты и физические константы.
2. Выбрать систему основных размерностей, через которую
выразить независимые переменные.
3. Составить безразмерные комбинации величин. Решение будет
правильным, если выполняются три условия:
● каждая комбинация действительно является безразмерной;
● число комбинаций не меньше, предсказываемого -теоремой;
● каждая переменная встречается хотя бы один раз.
4. Изучить комбинации с точки зрения их применимости
физического смысла. Составить план изменения комбинаций.
28
29. Примеры соотношений конвективного теплообмена
1. Гидродинамика вынужденного течения жидкости вканалах
Eu f (Re)
W l
Re
Eu
определяющее число подобия, критерий Рейнольдса;
p
2
( W )
определяемое число подобия, число Эйлера.
.
Если есть свободное движение под действием силы тяжести,
Eu f (Re, Fr )
критерий Фруда
Fr
g l
W2
29
30. Примеры соотношений конвективного теплообмена
2. Теплообмен при вынужденном теченииNu f (Re, Pr)
для сред с
Pr 1
Nu f ( Pe )
для сред с
Pr 1
определяющие числа подобия
число Рейнольдса
(Reynolds)
.
число Пекле
(Peclet)
W l
Re
число
Прандтля
.
(Prandtl)
W l
Pe Re Pr
a
определяемое число подобия, число Нуссельта
Nusselt
Pr
a
l
Nu
f
30
31. Примеры соотношений конвективного теплообмена
Критерий Пекле –(Peclet)
Pe
Wl
a
a c
Q1 W c F t W c
Pe
F t
Q2
l
l
Q1 Wc F t
Q2 F t
l
- количество тепла, переносимого
движущейся жидкостью, текущей со
скоростью W (конвективный перенос),
- количество тепла, переносимого
теплопроводностью через слой l.
31
32. Примеры соотношений конвективного теплообмена
Критерий Прандтля(Prandtl)
физ.свойство среды
Pr
a
кинематическая вязкость
температуропроводность
Перенос количества движения определяется разностью W.
Перенос тепла - разностью T.
Число Pr характеризует отношение между полями температуры
и скорости (подобие профилей скорости и температуры)
Три класса теплоносителей по Pr
Pr ~1 (вода, воздух).
Pr >>1 (масла).
Pr <<1 (жидкие металлы)
32
33. Выбор определяющих размеров и температур
Определяющий размерТеория подобия не дает указаний. Обычно это размер, который
отвечает существу процесса.
гидравлический диаметр
4F
dг
F - площадь сечения канала,
- смоченный периметр.
Определяющая температура
.
температура, при которой выбирают свойства среды
- .средняя по теплосодержанию температура потока
- средняя температура пограничного слоя:
tопр ( t f t w ) 2
33





























 physics
physics








