Similar presentations:
Геометрические приложения определенного интеграла. Лекция 13
1.
Первое высшее техническое учебное заведение РоссииСанкт-Петербургский горный университет императрицы Екатерины II
Раздел: Определенный интеграл
Лекция 13. Геометрические приложения
определенного интеграла
26.05.2025
г. Санкт-Петербург
2025
2.
Содержание лекции•Площадь плоской фигуры в прямоугольных координатах
•Площадь плоской фигуры, ограниченной параметрическими
уравнениями
•Полярная система координат
•Площадь криволинейного сектора
•Объем тела вращения
•Длина дуги кривой
•Площадь поверхности вращения
2
3.
Площадь плоской фигуры в прямоугольныхкоординатах
Криволинейная трапеция – фигура,
ограниченная графиком функции y=f(x),
осью Ох и прямыми х=а, х=b.
3
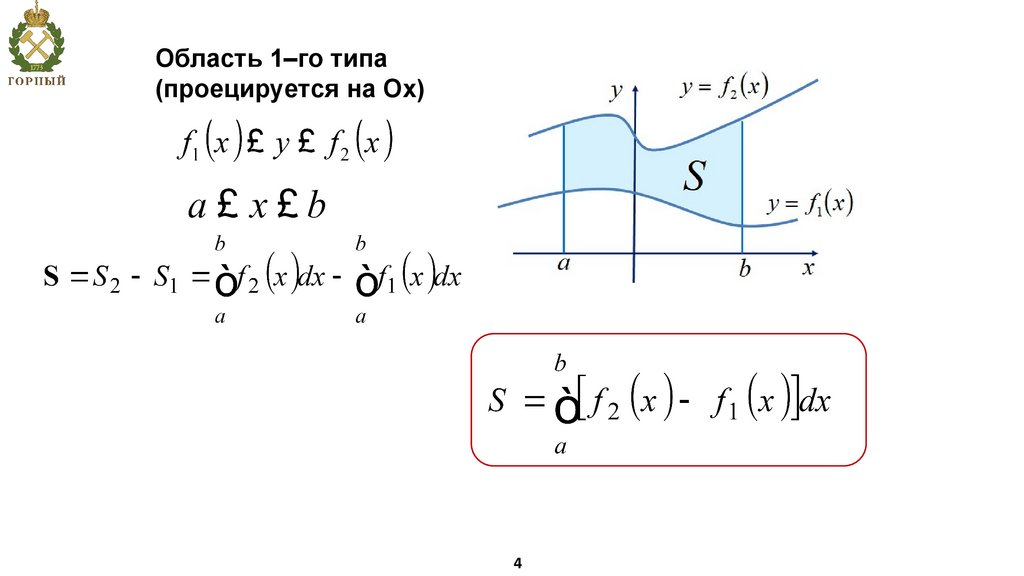
4.
Область 1–го типа(проецируется на Ох)
4
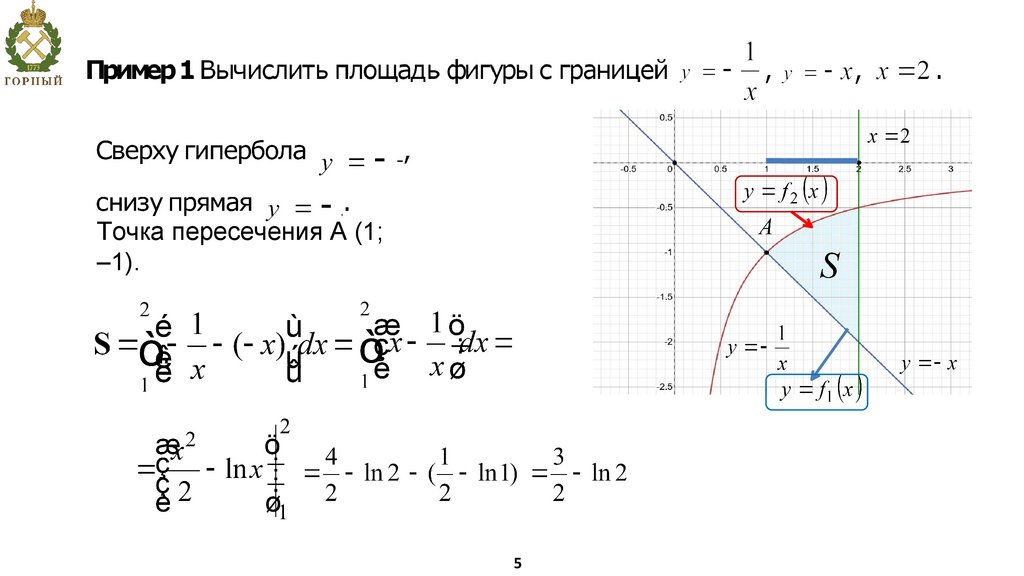
5.
Точка пересечения А (1;–1).
5
6.
Область 2–го типа(проецируется на Оу)
Если область сложная, то:
– разбить ее на конечное число областей 1-го и 2-го типа;
– найти сумму площадей простых подобластей.
6
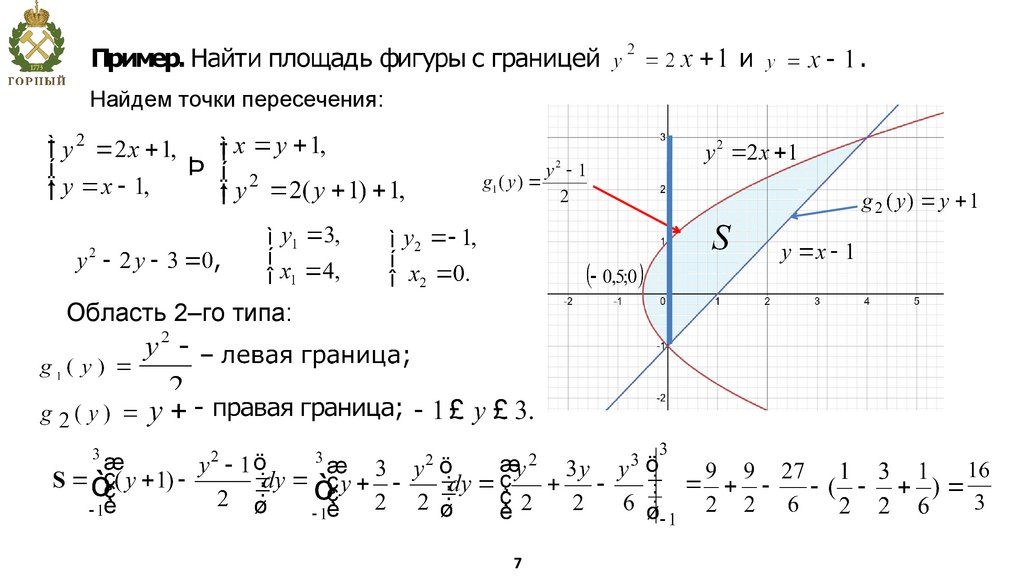
7.
Найдем точки пересечения:Область 2–го типа:
7
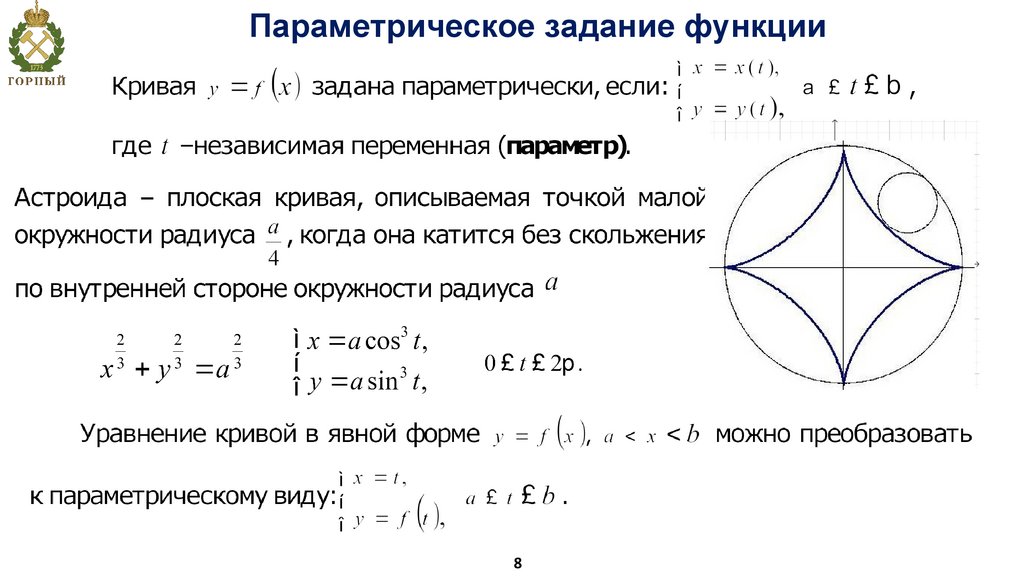
8.
Параметрическое задание функции8
9.
Площадь плоской фигуры, ограниченнойпараметрическими уравнениями
9
10.
1011.
1112.
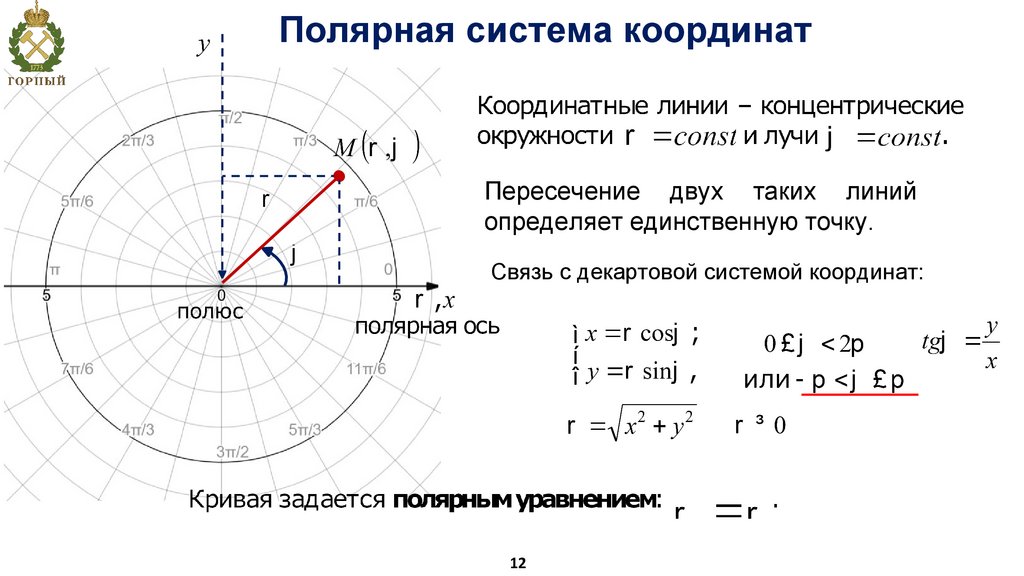
Полярная система координатПересечение двух таких линий
определяет единственную точку.
Связь с декартовой системой координат:
12
13.
Криволинейный сектор в полярной системе координат13
14.
Площадь криволинейного сектора в полярной системекоординат
14
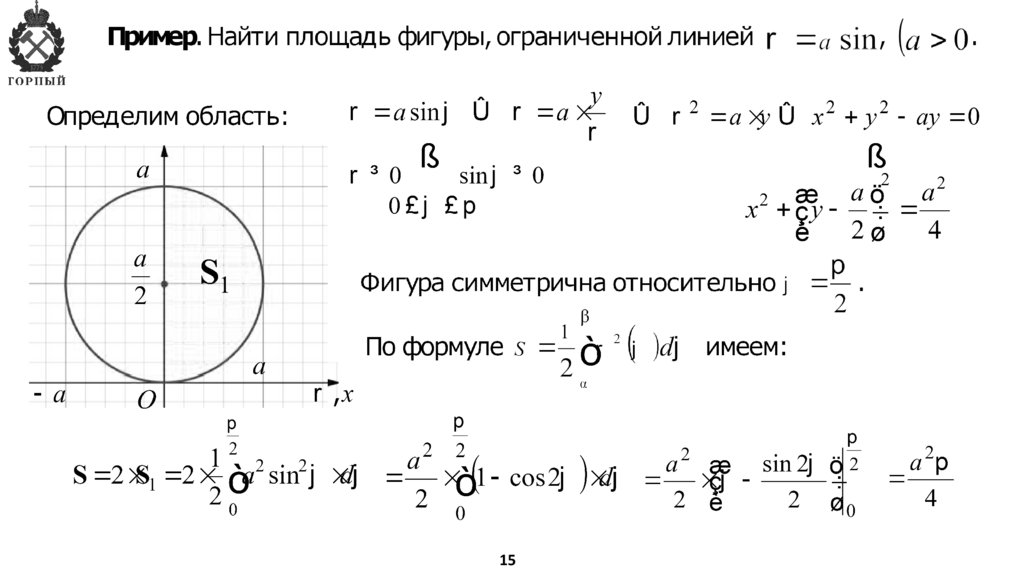
15.
1516.
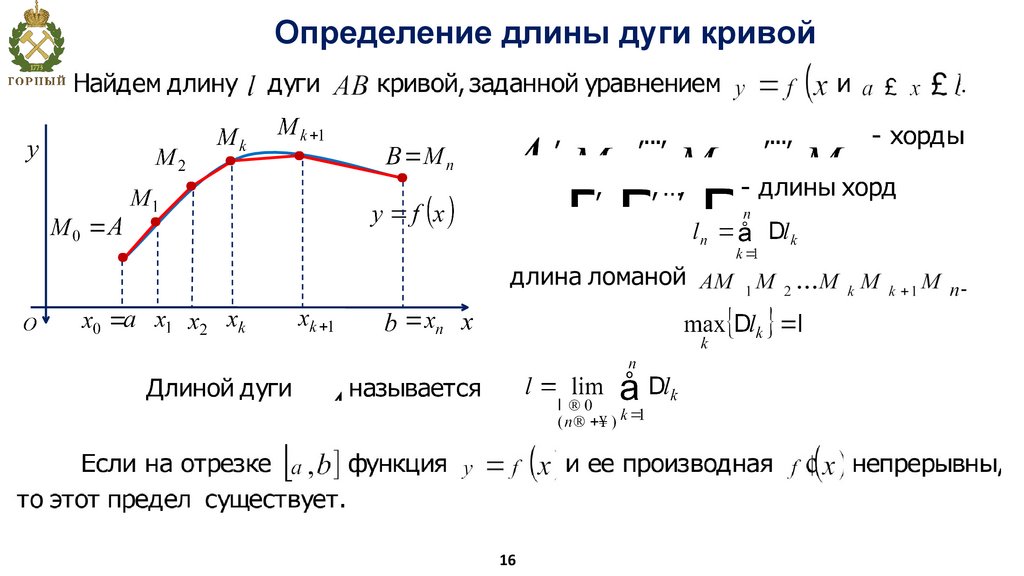
Определение длины дуги кривой16
17.
Длина дуги кривой17
18.
Длина дуги кривой, заданной параметрическиФункции x(t) и y(t) имеют непрерывные производные, причем
Замечание. Длина пространственной гладкой
кривой, заданной параметрическими уравнениями:
18
19.
Длина дуги кривой в полярных координатах19
20.
2021.
2122.
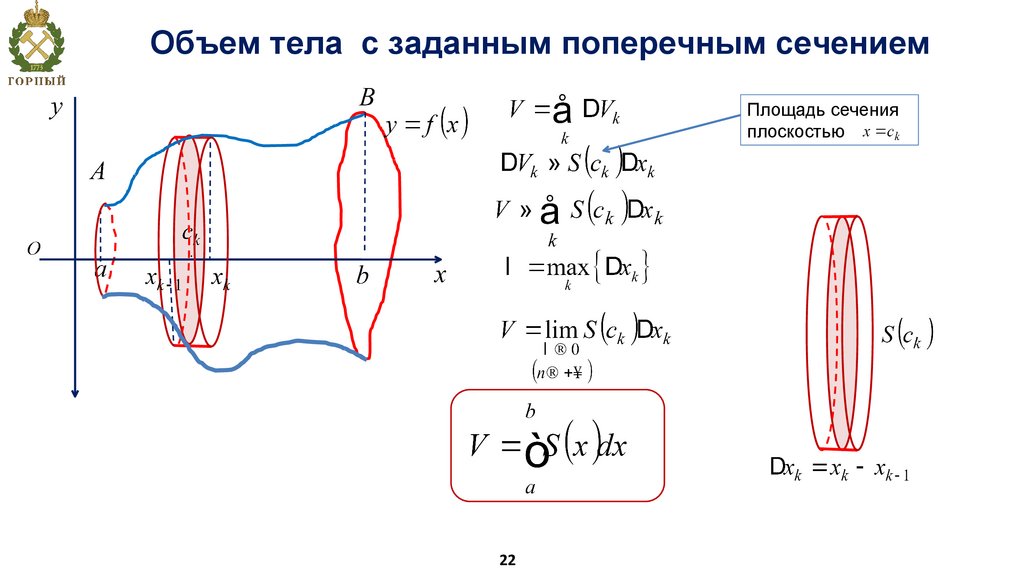
Объем тела c заданным поперечным сечениемПлощадь сечения
плоскостью
22
23.
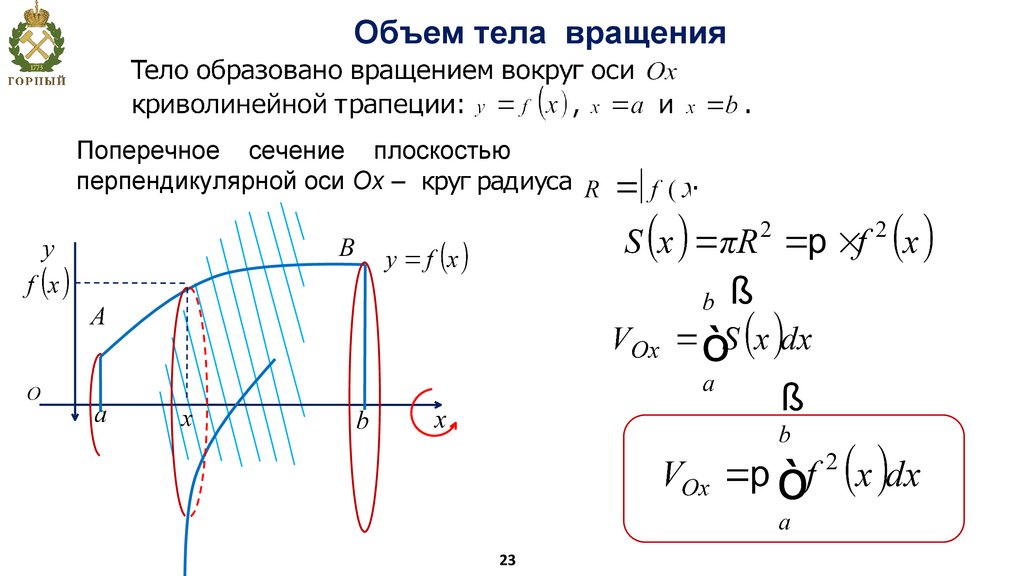
Объем тела вращенияПоперечное сечение плоскостью
перпендикулярной оси Ох –
23
24.
Объемтела
вращения
трапеции вокруг оси ординат:
24
25.
2526.
2627.
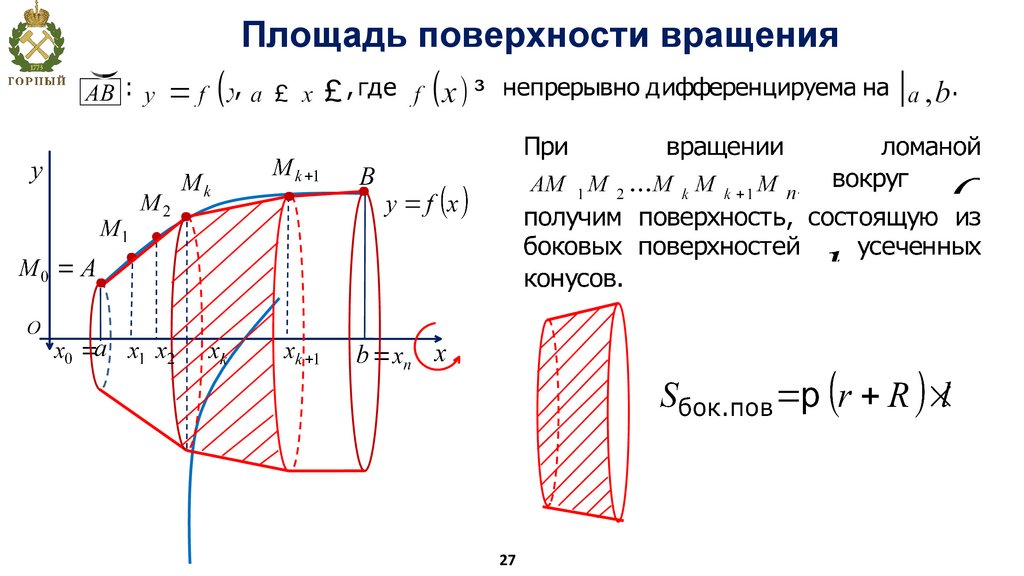
Площадь поверхности вращения27
28.
2829.
Площадь поверхности:Площадь поверхности:
29
30.
Кривая задана параметрическимиуравнениями:
Кривая задана
координатах:
в
полярных
30
31.
3132.
Первое высшее техническое учебное заведение РоссииСанкт-Петербургский горный университет императрицы Екатерины II
32|32






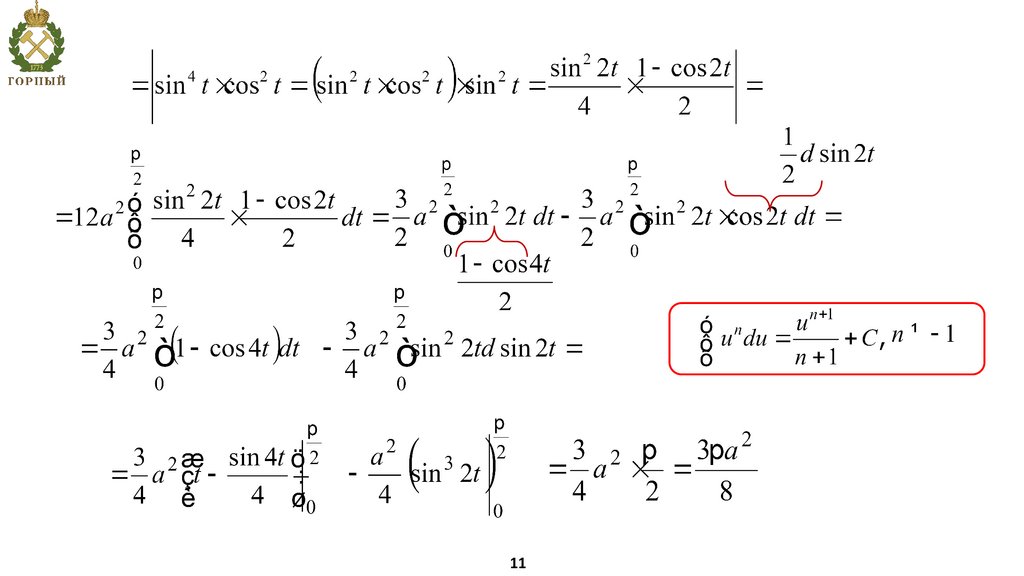















 mathematics
mathematics








