Статика жидкости. Понятие гидростатического давления

1. Статика жидкости. Понятие гидростатического давления

2. Темы лекции

• Общие условия равновесия.
• Напряженное состояние покоящейся жидкости.
Гидростатическо давление и его свойства.
• Уравнение равновесия жидкости.
• Основное уравнение гидростатики в
дифференциальной форме
• Равновесие однородной несжимаемой жидкости в
поле силы тяжести.
• Определение силы давления жидкости на
поверхности тел.
2

3. Цели занятия

• Умение применять уравнение равновесия жидкости.
• Способы определение силы давления жидкости на
поверхности тел.

4.

Гидравлика делится на два раздела: гидростатика и гидродинамика.
Гидродинамика является более обширным разделом и будет рассмотрена
в последующих лекциях. В этой лекции будет рассмотрена гидростатика.
Гидростатикой называется раздел гидравлики, в котором
рассматриваются законы равновесия жидкости и их практическое
применение.
Жидкости
всегда подвержены действию некоторых сил.
Вследствие текучести этих сред силы являются распределенными,
то есть действующим во всех точках поверхности или объема.
Рассмотрим силы, действующие на некоторый объем жидкой . В
зависимости от области приложения силы делятся
• внешние
• внутренние.
Внешние силы приложены к выделенному объему со стороны
внешней
среды,
внутренние
–
возникают
в
пределах
рассматриваемого объема.
4

5.

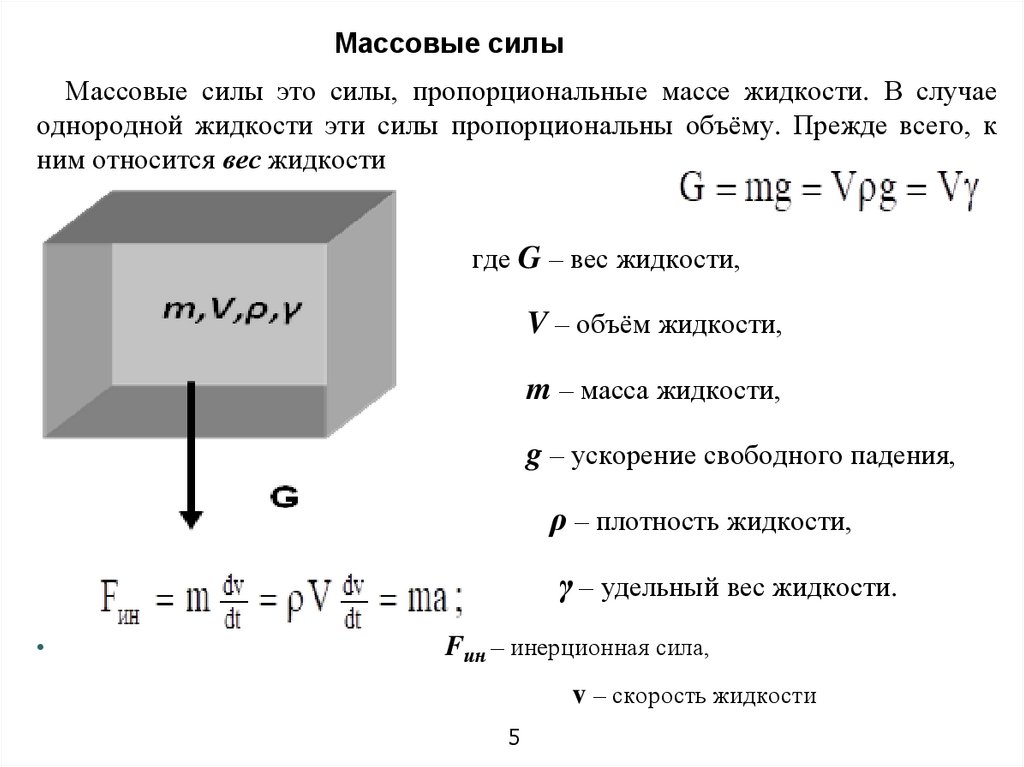
Массовые силы
Массовые силы это силы, пропорциональные массе жидкости. В случае
однородной жидкости эти силы пропорциональны объёму. Прежде всего, к
ним относится вес жидкости
где G – вес жидкости,
V – объём жидкости,
m – масса жидкости,
g – ускорение свободного падения,
ρ – плотность жидкости,
γ – удельный вес жидкости.
Fин – инерционная сила,
v – скорость жидкости
5

6.

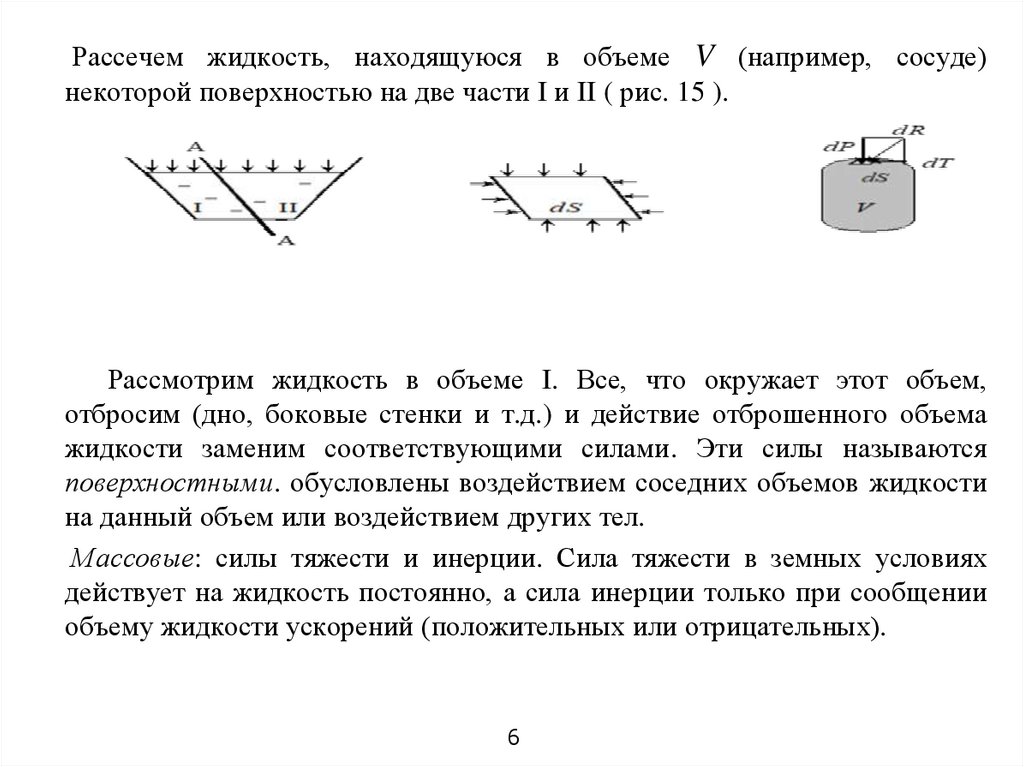
Рассечем жидкость, находящуюся в объеме V (например, сосуде)
некоторой поверхностью на две части I и II ( рис. 15 ).
Рассмотрим жидкость в объеме I. Все, что окружает этот объем,
отбросим (дно, боковые стенки и т.д.) и действие отброшенного объема
жидкости заменим соответствующими силами. Эти силы называются
поверхностными. обусловлены воздействием соседних объемов жидкости
на данный объем или воздействием других тел.
Массовые: силы тяжести и инерции. Сила тяжести в земных условиях
действует на жидкость постоянно, а сила инерции только при сообщении
объему жидкости ускорений (положительных или отрицательных).
6

7.

Выделим из жидкости некоторый объем. Возьмем на поверхности этого
объема бесконечно малую площадку dS. Hа эту площадку действует
поверхностная сила dR. Разложим эту силу на нормальную dP и
касательную dT.
Hормальная сила, приходящаяся на единицу площади,
называется давлением и обозначается буквой p, т.е.
Сила трения (касательная сила), приходящаяся на единицу площади,
обозначается буквой , .
Сила трения обычно пропорциональна градиенту скорости
Для жидкости, находящейся в равновесии (в покое), сила трения равна
нулю, так как в этом случае
7

8.

Если давление Р отсчитывают от абсолютного нуля, то его называют
абсолютным давлением Рабс. Если давление отсчитывают от атмосферного,
то оно называется избыточным Ризб. Атмосферное давление постоянно Ра =
103 кПа.
Кроме того, различают давление гидродинамическое и
гидростатическое. Гидродинамическое давление возникает в движущейся
жидкости. Гидростатическое давление – давление в покоящейся жидкости.
Схема к определению давлений
1 Па = 1 Н/м² = 10-3 кПа = 10-6 МПа. = 0,102 кгс/м² или 1 кгс/м² = 9,81 Па.
8

9.

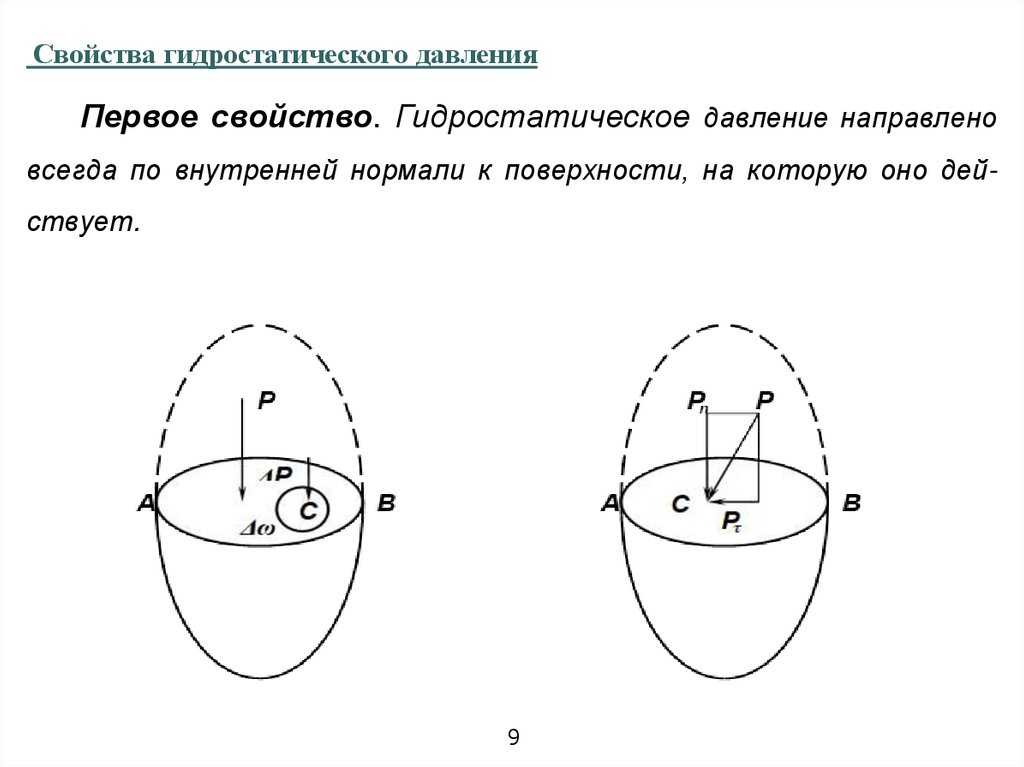
Свойства гидростатического давления
Первое свойство. Гидростатическое давление направлено
всегда по внутренней нормали к поверхности, на которую оно дей-
ствует.
9

10. Гидростатическое давление и его свойства

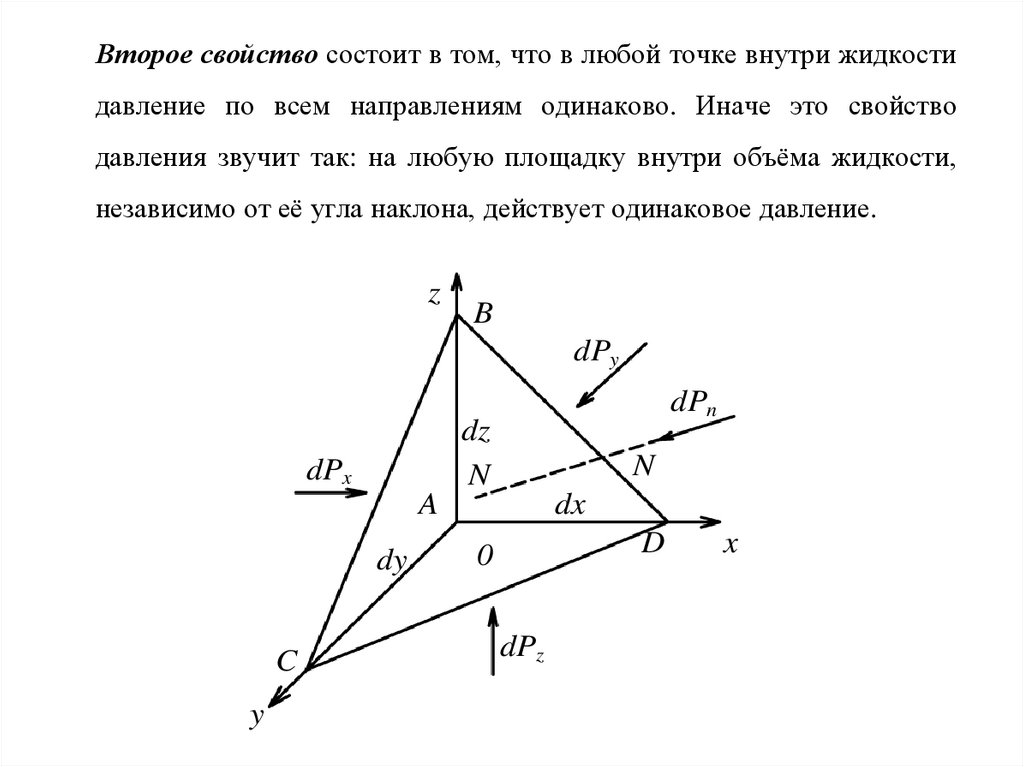
Второе свойство состоит в том, что в любой точке внутри жидкости
давление по всем направлениям одинаково. Иначе это свойство
давления звучит так: на любую площадку внутри объёма жидкости,
независимо от её угла наклона, действует одинаковое давление.
z
B
dPy
dPn
dz
N
dPx
N
dx
A
dy
C
y
D
0
dPz
x

11.

Воспользуемся известными уравнениями статики твердого тела, а
именно уравнениями проекций сил и уравнениями моментов:
Учитывая, что при стягивании тетраэдра в точку, уравнения моментов
такой системы удовлетворяются тождественно, а действующие на него
силы сводятся к системе сил, проходящих через одну и ту же точку.
Таким образом, остается только три проекции сил:
К действующим силам относятся поверхностные и массовые силы.
11

12. Гидростатическое давление и его свойства

К поверхностным силам относятся силы давления жидкости,
окружающей элементарный тетраэдр.
Таких сил будет четыре (по числу граней).
На грань АВС действует сила
1
Px p x dydz,
2
Четвертая сила dPn– сила давления на грань ВСD равна: dPn = pnd ,
проекция силы dPnна ось ox
1
dPn cos N , ox pn dydz.
2
1
dPn cos N , oy pn dxdz;
2
1
dPn cos N , oz pn dxdy.
2

13. Гидростатическое давление и его свойства

• Массовые силы
1
dm dxdydz,
6
• Обозначим проекции ускорения j по координатным осям x,y,z, т.е.
примем, что
- jcos = X;
- jcos = Y;
-jcos = Z.
Запишем сумму проекций всех сил на ось ox
Fx p
1
1
1
dydz pn dydz dxdydzX 0.
2
6
x2
После сокращений
px= py= pz= pn.

14.

Третье свойство. Гидростатическое давление в точке зависит только
от ее координат в пространстве, т. е.
Это свойство не требует специального доказательства, так как
очевидно, что по мере увеличения заглубления точки под вровень
давление в ней будет возрастать и, наоборот, по мере уменьшения
заглубления — уменьшаться.
14

15. Гидростатическое давление и его свойства

• Разделяется давление:
абсолютное, избыточное и давление вакуума.
абсолютное давление - давление в точке измерения,
отсчитанное от нуля.
избыточное давление - разница между абсолютным
давлением и атмосферным: pизб = pабс – pА .
• давление вакуума - разница между замеренным
давлением и атмосферным называется давлением
вакуума: pвак = pА – pабс.

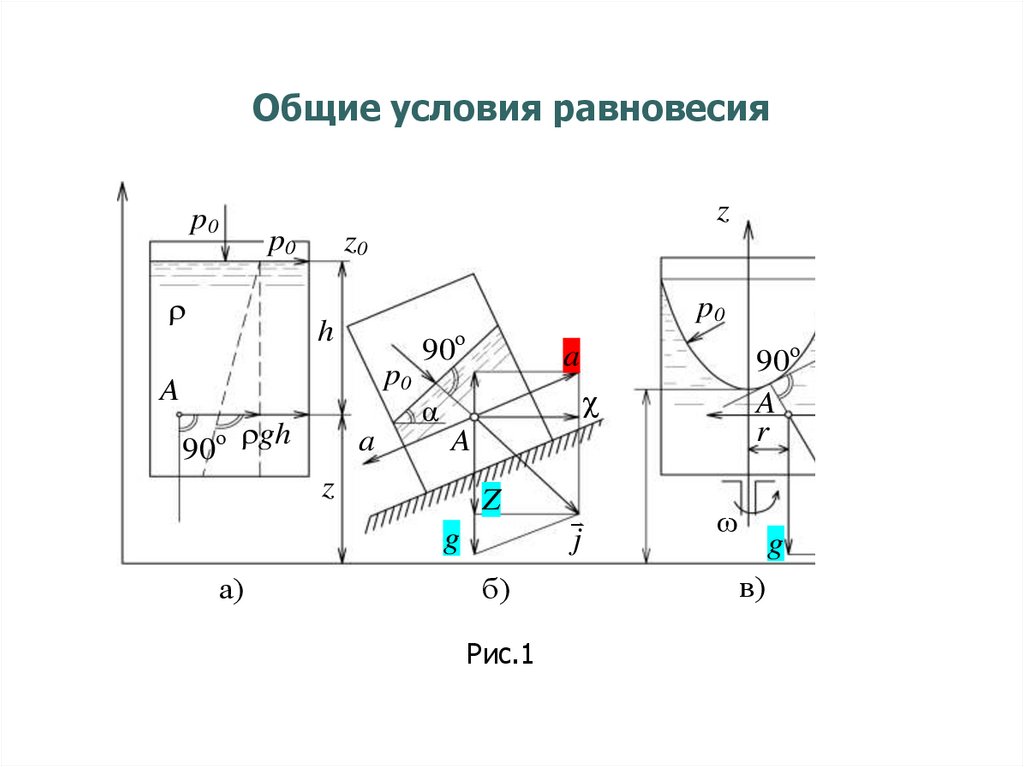
16. Общие условия равновесия

• Различают:
- абсолютное равновесие жидкости, т.е. равновесие
относительно сосуда, двигающегося равномерно и
прямолинейно или покоящегося относительно земли
(рис. 1 а),
относительное
равновесие
–
равновесие
относительно сосуда, движущегося прямолинейно с
постоянным ускорением относительно земли (рис. 1
б) или относительно сосуда, вращающегося с
постоянной угловой скоростью ω, относительно своей
оси (риc.1 в)

17. Общие условия равновесия

z
z
p0
p0
z0
p0
h
p0
A
90о
χ
α
90о gh
a
A
z
Z
g
а)
90о
A
r
a
б)
Рис.1
j
ω
g
в)
χ
j
x

18. Общие условия равновесия

Жидкость может сохранять свое равновесное состояние в том случае,
если внешние силы, действующие в точках граничной поверхности,
направлены только по внутренним нормалям к этой поверхности.
Очевидно, что действие силы давления по внешней нормали приводит к
нарушению равновесия, т.к. жидкость не оказывает сопротивления
растягивающим силам. Касательные силы возникают при движении
жидкости, поэтому при равновесии жидкости, находящейся в покое, они
равны нулю.
В основу гидростатики положены две теоремы:
- равенство нулю суммы всех сил, приложенных к
рассматриваемому элементу жидкости
- равенство нулю суммы моментов этих сил относительно какойто оси.

19. Дифференциальное уравнение равновесия жидкости (ур-е Эйлера)

• Выделим в жидкости элементарный объем в виде прямоугольного
параллелепипеда с ребрами, параллельными осям координат и
равными dx, dy, dz. Полагая его твердым телом, составим три уравнения
проекций действующих сил :
F x = 0; F y = 0; F z = 0.
равнодействующая единичная массовая сила- X, Y, Z.
z
С
С1
В1
В
p1
p
D
dz
А
dy
y
D1
dx
А1
x

20.

Равновесие параллелепипеда обеспечивается шестью проекциями
(по числу граней).
В уравнение
= 0 войдут только две силы: dP и dP .
Сила давления на грань ABCD
Сила давления на грань A B C D
Следовательно
тогда
Проекции объемных сил.
Проекция объемной силы dR равна произведению массы на
соответствующую проекцию ускорения объемной силы, т.е.
X – проекция ускорения силы dR на ось Ох.
dx, dy, dz – объем выделенного элемента;
20

21.

Сумма проекций поверхностных и объемных сил на ось Ох равна:
уравнение проекций сил на ось Ох, отнесенных к единице объема:
Аналогично получим два других уравнения:
=0,
=0.
Таким образом, при равновесии жидкости имеем три дифференциальных
уравнения:
Система уравнений равновесия жидкости относится как к
несжимаемой, так и к сжимаемой жидкости.
Эта система уравнений впервые была получена Эйлером в 1755 г.
21

22. Уравнение Эйлера

1 p
X
0;
x
1 p
Y
0;
y
1 p
Z
0.
z
В векторной форме данная системы дифференциальных
уравнений Эйлера для гидростатики

23. Основное уравнение гидростатики в дифференциальной форме.

Умножим каждое из уравнений на dx, dy и dz соответственно и
просуммируем их
Xdx Ydy Zdz 1 p dx p dy p dz 0.
x
y
z
полный дифференциал давления
dp Xdx Ydy Zdz .
жидкость находится в состоянии равновесия, то правая часть
является полным дифференциалом какой-то функции Uпотенциальной, или силовой функцией, а силыимеющие
потенциал.
dp = dU.
Силы, работа которых не зависит от пути движения, а только от
начального и конечного положений, называют потенциальными. Из
вышеизложенного следует, что равновесие жидкости возможно
только в том случае, когда массовые силы имеют потенциал.

24. Основное уравнение гидростатики в дифференциальной форме.

поверхностью
уровня
- поверхность, точки которой имеют
одинаковые значения данной функции. К поверхности равного уровня
относятся:
– поверхности равного давления;
– изотермические поверхности (поверхности равной температуры);
– поверхности равной плотности и т.д.
эквипотенциальные поверхности, в каждой точке которых U = const,.
Частным
случаем
эквипотенциальной
поверхности
является
поверхность равного давления, т.е. поверхность, в каждой точке
которой p =const. В этом случае dp = 0 и принимает вид:
Xdx Ydy Zdz 0.

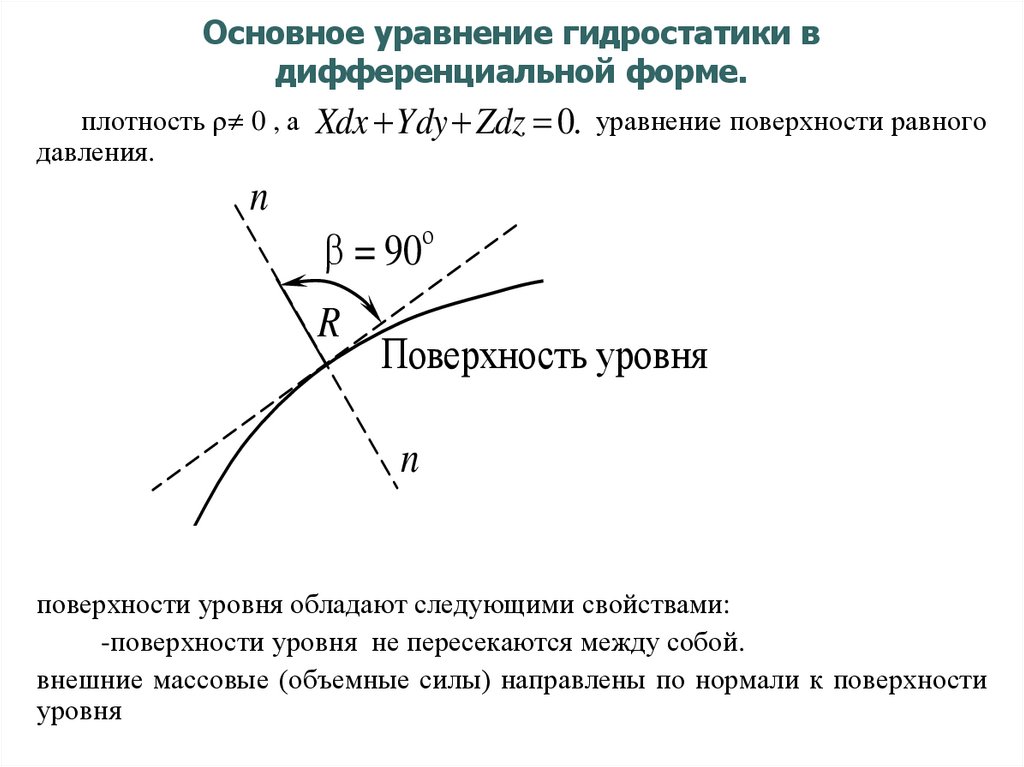
25. Основное уравнение гидростатики в дифференциальной форме.

плотность 0 , а Xdx Ydy Zdz 0. уравнение поверхности равного
давления.
n
= 90о
R
Поверхность уровня
n
поверхности уровня обладают следующими свойствами:
-поверхности уровня не пересекаются между собой.
внешние массовые (объемные силы) направлены по нормали к поверхности
уровня

26.

Равновесие жидкости в поле земного тяготения
В качестве объемной силы в поле земного тяготения выступает сила
тяжести.
Полное ускорения объемных сил равно ускорению свободного падения: g =
9,81 м/c2.
В выбранной системе координат проекции единичной объемной силы на
оси Ox, Oy и Oz будут следующими:
.
Знак «минус» в ускорении свободного падения соответствует направлению
силы тяжести в отрицательную сторону оси Oz.
Подставляя значения X, Y, Z в уравнение поверхности уровня получим
и следовательно,
26

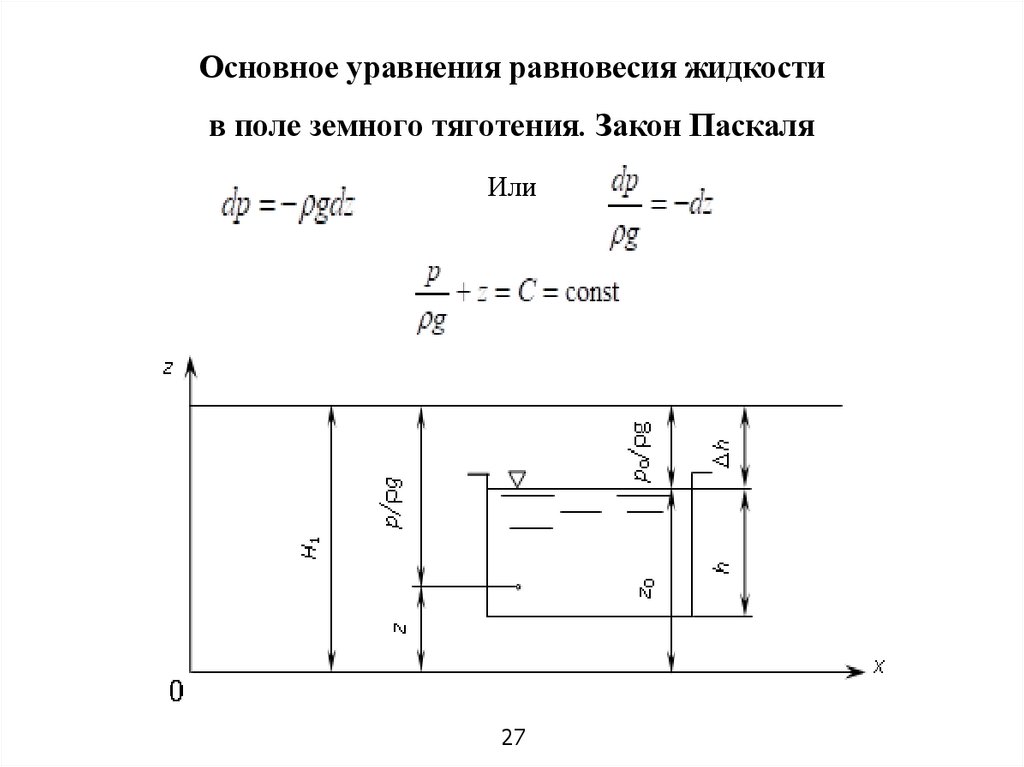
27.

Основное уравнения равновесия жидкости
в поле земного тяготения. Закон Паскаля
Или
27

28.

Постоянную
интегрирования
найдем
из
граничных
условий. Для
свободной поверхности жидкости имеем:
где
давление на свободной поверхности жидкости,
р0 – р0 = ратм.
Следовательно
Решая совместно уравнения , получаем
Это уравнение называется основным уравнением равновесия жидкости
в поле тяготения. Обычно уравнение записывается в форме
28

29. Равновесие однородной несжимаемой жидкости в поле силы тяжести

закон Паскаля:
давление, приложенное к свободной поверхности,
передается во все точки без изменения.
• абсолютное давление - сумма барометрического (атмосферного)
давления и избыточного
pабс = pбар pизб.
Вакуум - отрицательное избыточное давление.
• z - геометрический напор;
• p/ g – пьезометрический напор.
p гидростатический напор.
z
g

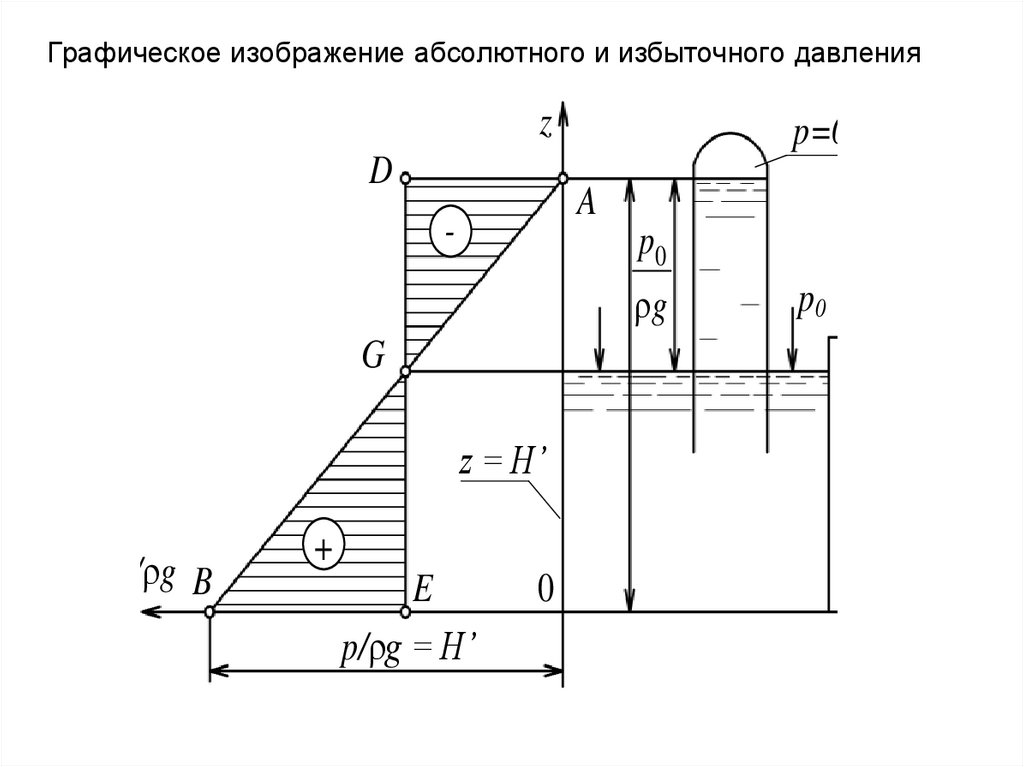
30. Равновесие однородной несжимаемой жидкости в поле силы тяжести

Графическое изображение абсолютного и избыточного давления
z
D
p=0
A
-
p0
g
p0
G
z = H’
p/ g B
+
E
p/ g = H’
0
x

31. Равновесие однородной несжимаемой жидкости в поле силы тяжести

• Треугольник OAB выражает закон изменения
абсолютного давления, а два треугольника с общей
вершиной в точке G символизируют закон изменения
избыточного давления:
- нижний треугольник BGE выражает pизб/ g 0,
- верхний pизб/ g 0.
Величина гидростатического давления (полного или
избыточного) может быть выражена тремя способами:
- в единицах силы, действующей на единицу
н , кгс , кгс
площади, например
м 2 м 2 см 2
- в атмосферах; в гидравлике используется
техническая атмосфера
1ат 1 кгс2 9,81.10 4 н2
см
м

32. Равновесие однородной несжимаемой жидкости в поле силы тяжести

• высотой
столба
жидкости,
называется
пьезометрической
высотой , м.вод.ст.
• соотношения между единицами измерения давления:
1 кгс 1ат 9,81.10 4 н 10 м вод.ст. = 735 мм рт. ст.
см 2
м2
1 н 1,02.10 5 ат 1,02.10 5 кгс =1,02.10-4мвод.ст.
м2
см2

33.

Избыточное давление
Избыточным (или манометрическим) давлением называется разность между
полным (абсолютным) и атмосферным (барометрическим) давлением
Если полное давление p меньше атмосферного pат, то избыточное давление
будет отрицательным. Отрицательное избыточное давление, т.е. недостаток
давления до атмосферного, называется вакуумом (вакуумметрическим
давлением, разрежением)
Абсолютная величина вакуума может изменяться в пределах от 0 до pат
при p=0 имеем pвак=pат,
а при p=pат имеем pвак=0.
33

34.

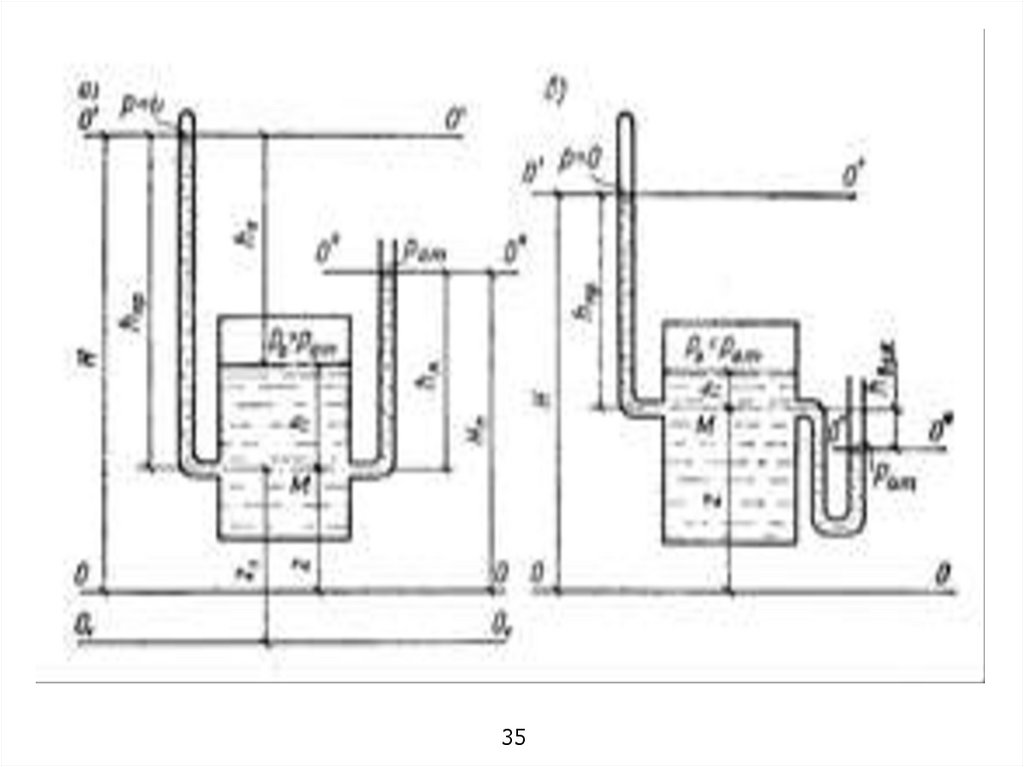
Если жидкость находится в закрытом резервуаре и давление на ее
свободной поверхности po больше атмосферного pат (рис,) то избыточное
давление жидкости на стенку резервуара в любой точке будет равно:
=
где: (po – pат) – есть избыточное давление на свободной поверхности
жидкости.
Если в закрытом резервуаре давление на свободной поверхности po
меньше атмосферного pат, то избыточное давление будет равно
Когда давление на свободной поверхности жидкости равно
атмосферному po=pат (открытый резервуар, водоем), избыточное
давление будет равно (рис. ):
34

35.

35

36.

На законе Паскаля основан принцип действия различных гидравлических устройств, с помощью которых давление передается на
расстояние.
К таким устройствам относятся: гидравлические прессы, гидроподъемники,
гидродомкраты,
гидравлические
аккумуляторы,
равлические тормозные системы, гидромультипликаторы и др.
36
гид-

37.

К поршню площадью F приложена сила Р1, которая передается жидкости,
создавая давление р1:
По закону Паскаля давление передается на поршень площадью F2,
создавая полезную силу, под действием которой прессуется материал:
Следовательно
или
Из формулы видно, что отношение усилий на малом и большом поршнях
пропорционально квадрату отношения диаметров поршней.
37

38.

Относительное равновесие жидкости
в поле сил тяготения
Относительным равновесием жидкости называется такое состояние, при
котором каждая ее частица сохраняет свое положение относительно твердой
стенки движущегося сосуда.
При относительном равновесии надо решить две задачи.
•1. Определить форму поверхности уровня.
•2. Установить характер распределения давления.
Решение этих задач основано на дифференциальных уравнениях
равновесия .
При относительном равновесии следует учитывать силы инерции,
дополняющие систему массовых сил, действующих в жидкости,
находящейся в состоянии абсолютного покоя.
38

39.

Равноускоренное движение по вертикали.
Их проекции или проекции ускорений X = 0; Y = 0; Z = (–g j)
(при спуске (+j) и при подъеме (–j)).
Уравнение поверхности уровня имеет вид
Если g j, то dz = 0, а потому
z c const .
Это уравнение семейства горизонтальных плоскостей, как при
подъеме, так и при спуске поверхности уровня.
39

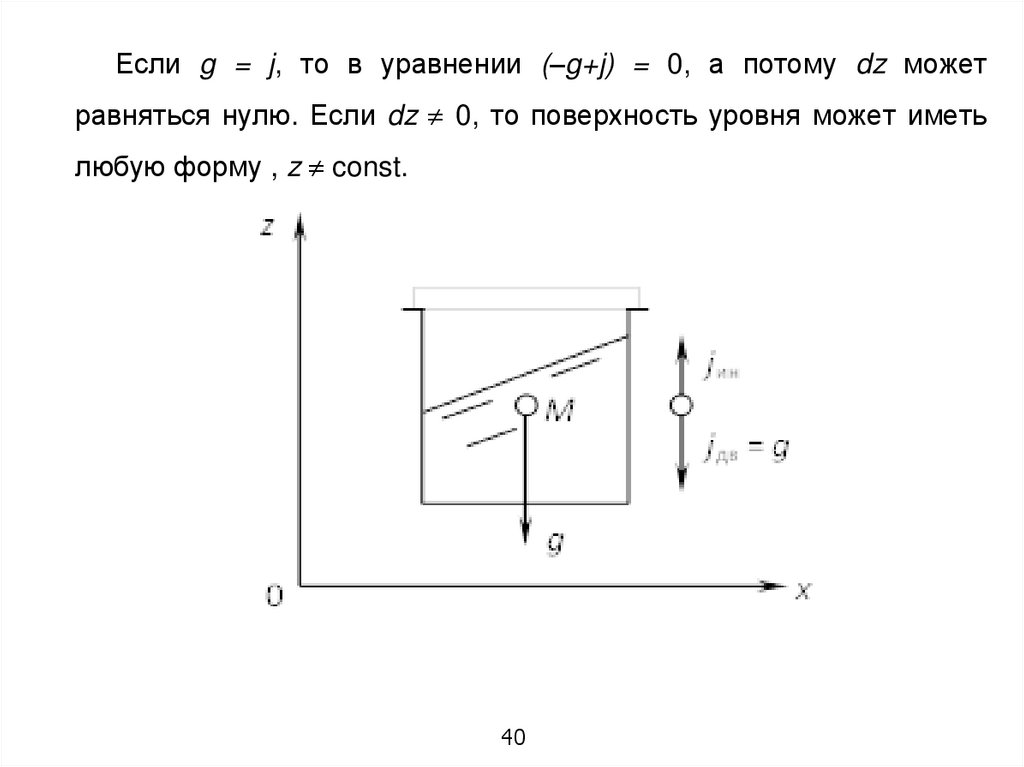
40.

Если g = j, то в уравнении (–g+j) = 0, а потому dz может
равняться нулю. Если dz 0, то поверхность уровня может иметь
любую форму , z const.
40

41.

Закон распределения давления
С учетом того, что X = 0; Y = 0; Z = (–g j), уравнение преобразуется к
виду:
При равноускоренном движении (спуске) (–g+j)
а при равноускоренном подъеме (–g – j)
Анализ уравнений показывает, что произведение
можно рассматривать как условный вес, отнесенный к единице
объема жидкости.
Обозначим его , тогда при спуске ( j < g), жидкость оказывается
как бы более легкой,
а при j = g получим
стала невесомой .
и, следовательно, = 0, поэтому жидкость
41

42.

Пример 1 Определить уравнение свободной поверхности жидкости в
сосуде, движущемся горизонтально с ускорением «а».
На жидкость действуют сила тяжести и сила инерции, т.е
Имеем
Откуда
уравнение прямой
Следовательно, свободная поверхность представляет собой плоскость,
наклоненную к горизонту под углом , который определяется из равенства
42

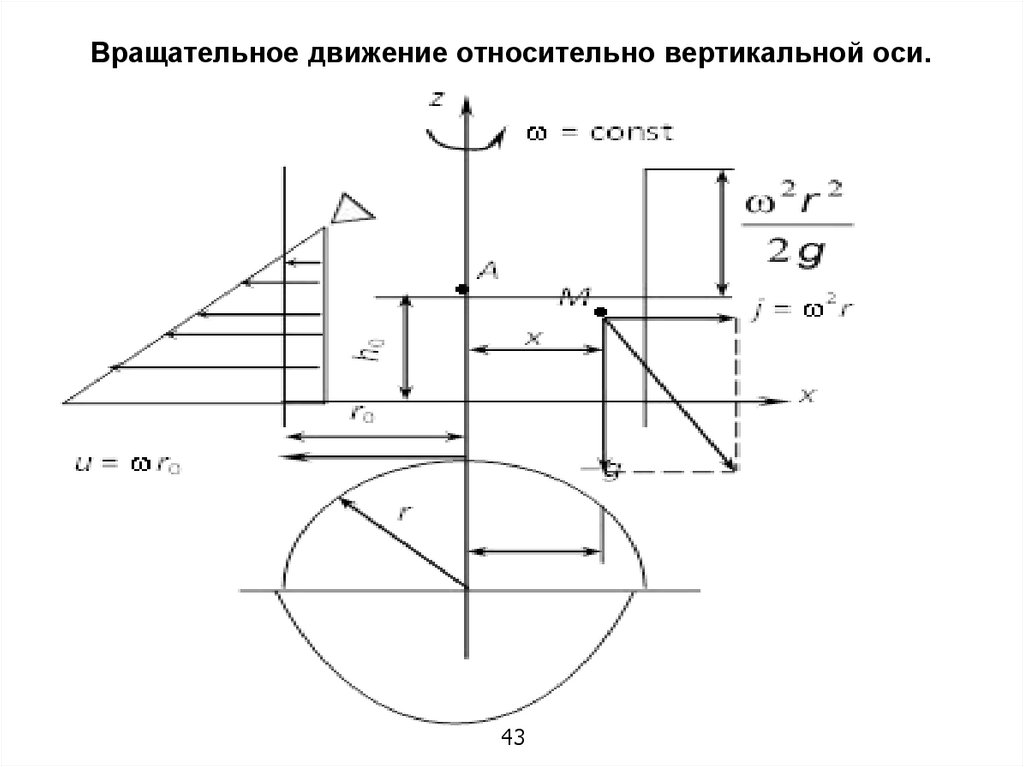
43.

Вращательное движение относительно вертикальной оси.
43

44.

С учетом осесимметричности движения относительно оси oz
уравнение можно записать в цилиндрических координатах:
где Z = –g – ускорение свободного падения;
R – проекция ускорения центробежной силы, равного
u – окружная скорость;
r – радиус вращения.
Учитывая, что u = r, имеем:
уравнение поверхности в данном случае имеет вид:
Интегрируя это уравнение, получим
Это уравнение представляет собой параболу в плоскости roz.
44

45.

С учетом равенства
уравнение свободной поверхности име-
ет вид:
где h – глубина на расстоянии r от оси вращения.
Таким образом, глубина h увеличивается с увеличением расстояния от оси.
45

46.

Закон распределения давления
dp Xdx Ydy Zdz .
Тогда
или
После интегрирования и изменения порядка слагаемых получим
принимая r=0, z=h0 и p=p0, получим
или
Из уравнения видно, что для любого заданного r=const, закон распределения давления по высоте является
линейным.
46

47.

Пример 2. Определить уравнение свободной поверхности жидкости в
сосуде, вращающемся вокруг вертикальной оси с угловой скоростью .
Вследствие трения о стенки сосуда жидкость будет вращаться с такой
же угловой скоростью. Жидкость будет находиться в относительном покое.
Поэтому при решении задачи применимы уравнения равновесия.
Из массовых сил на жидкость действует центробежная сила и сила
тяжести. Центробежная сила, действующая на массу m, находится на
расстоянии r от оси вращения.
свободная поверхность - параболоид вращения.
47

48.

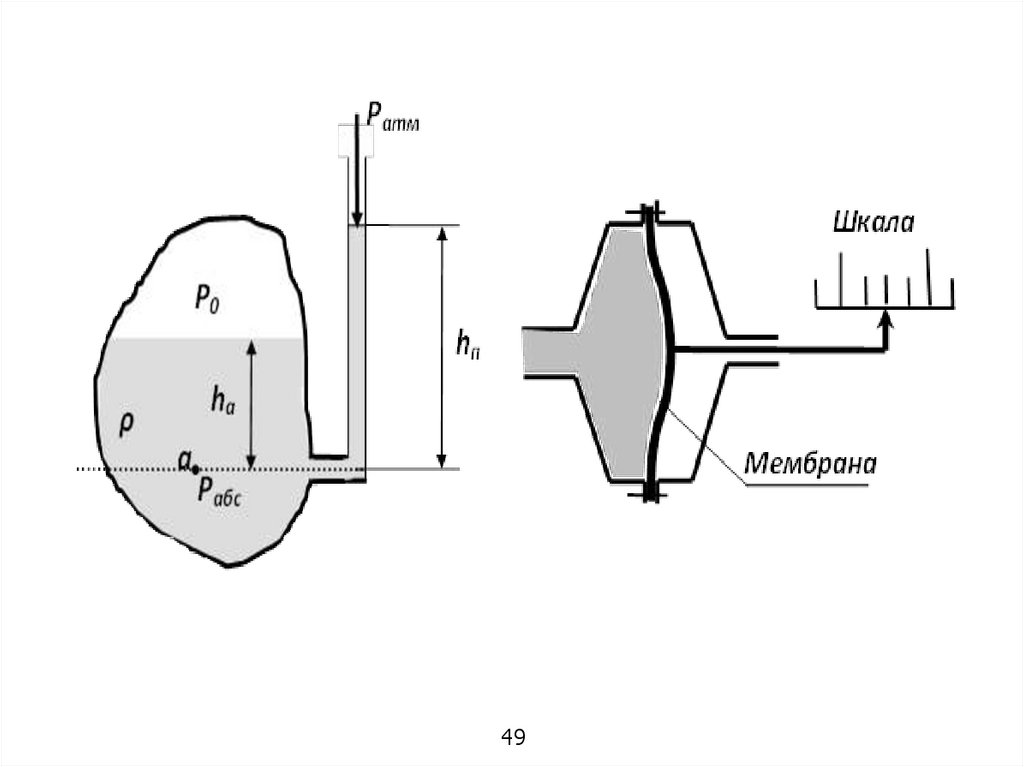
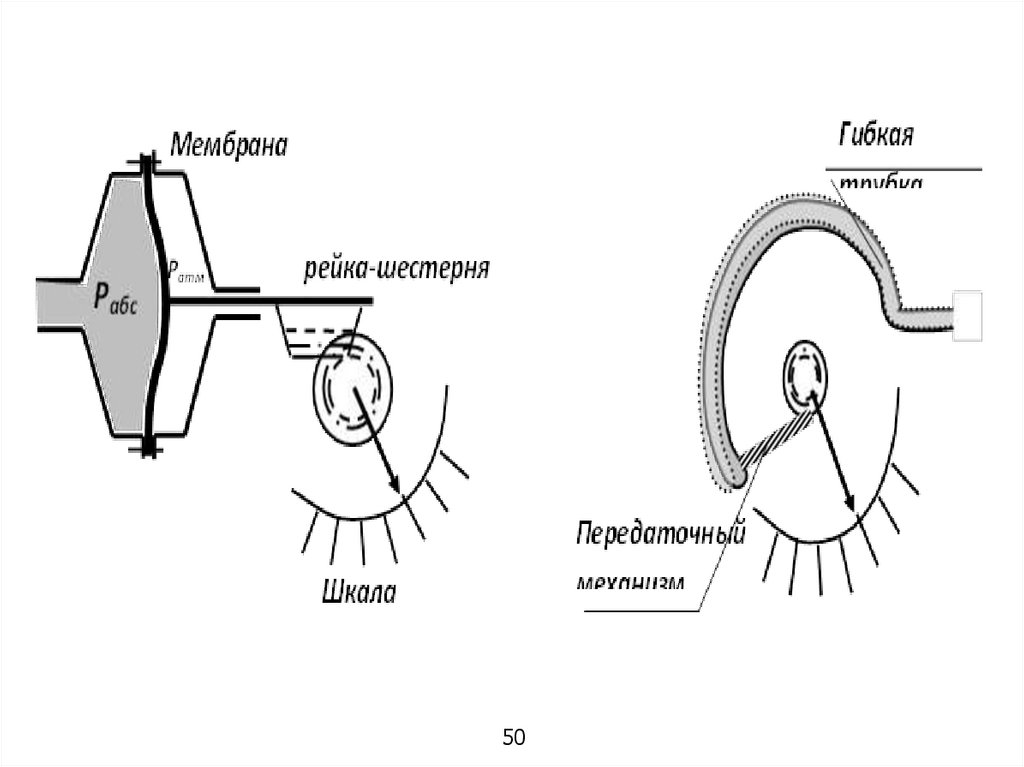
Приборы для измерения давления
Существует два основных типа приборов для измерения давления в
жидкости. К приборам первого типа можно отнести пьезометры. Они
представляют собой вертикальную трубку, обычно прозрачную.
с другой стороны
Отсюда
Величина
называется пьезометрической высотой.
Если абсолютное давление меньше атмосферного
такое давление называют вакуумметрическим давлением
высоту в пьезометре называют вакуумметрической высотой
48

49.

49

50.

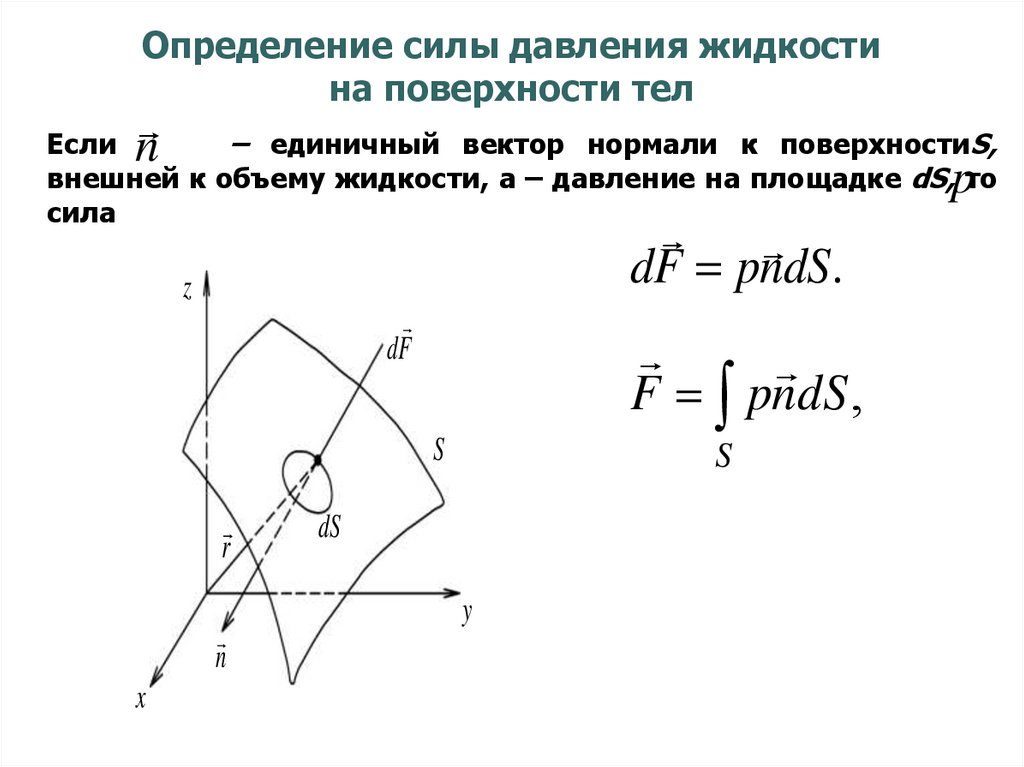
50

51. Определение силы давления жидкости на поверхности тел

n
Если
– единичный вектор нормали к поверхностиS,
внешней к объему жидкости, а – давление на площадке dS, то
сила
p
dF pndS.
z
dF
F pndS ,
S
r
n
x
S
dS
y

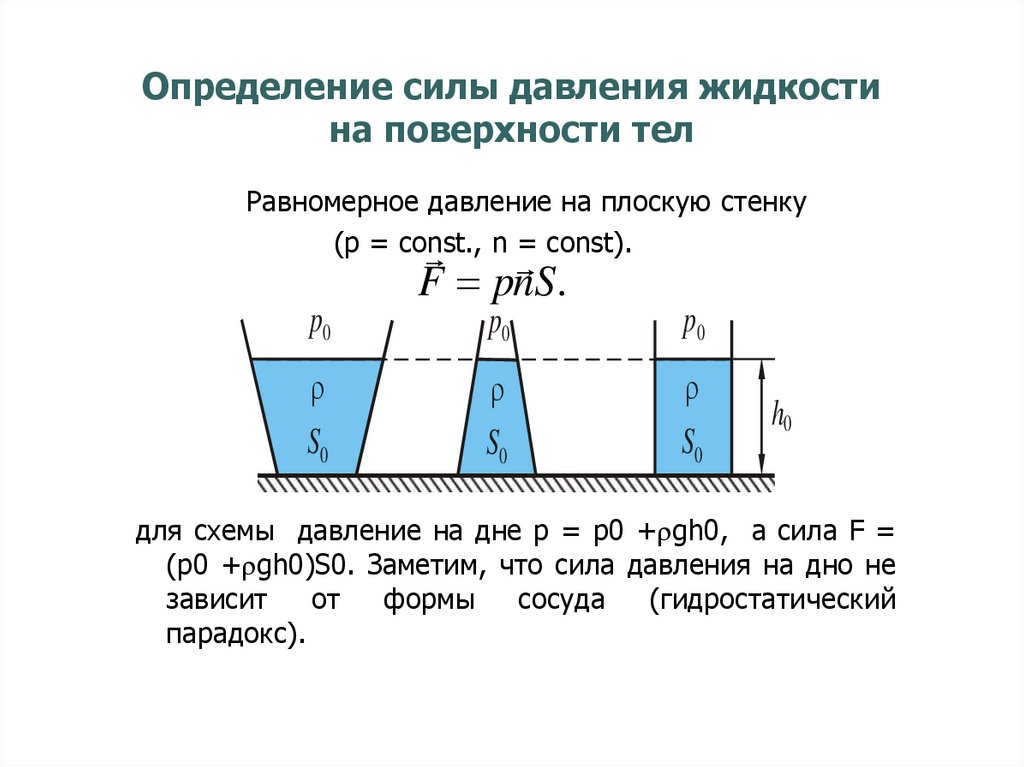
52. Определение силы давления жидкости на поверхности тел

Равномерное давление на плоскую стенку
(p = const.,
n = const).
F pnS.
p0
p0
p0
S0
S0
S0
h0
для схемы давление на дне p = p0 + gh0, а сила F =
(p0 + gh0)S0. Заметим, что сила давления на дно не
зависит
от
формы
сосуда
(гидростатический
парадокс).

53. Copyright

Внимание. Данный дидактический материал предназначен для личного использования
студентом и защищен законом об авторских правах. Согласно данному закону частичное
или полное воспроизведение данного материала в иных целях строго запрещено.
Copyright©UNIMARCONI
53