Первообразная. Интеграл. Метод интегрирования по частям

1. Первообразная Интеграл Метод интегрирования по частям

2. Содержание

Понятие первообразной
Неопределенный интеграл
Таблица первообразных
Три правила нахождения первообразных
Определенный интеграл
Вычисление определенного интеграла
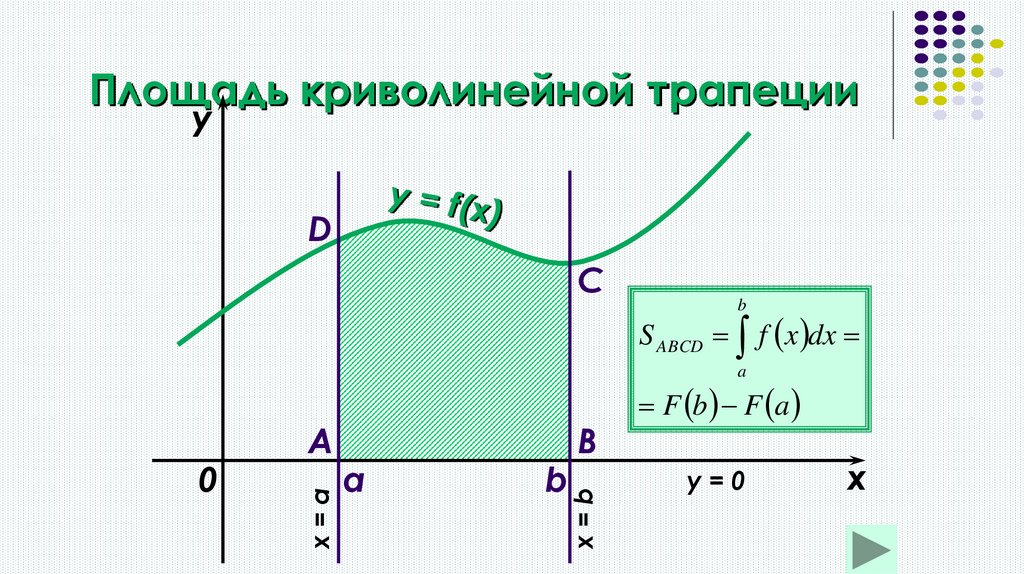
Площадь криволинейной трапеции
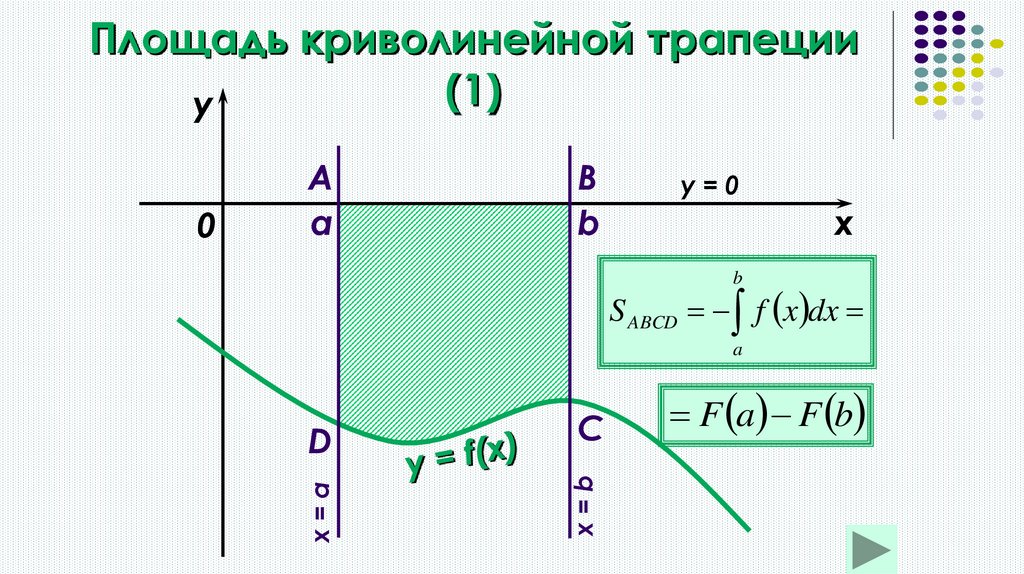
Площадь криволинейной трапеции (1)
Площадь криволинейной трапеции (2)
Площадь криволинейной трапеции (3)
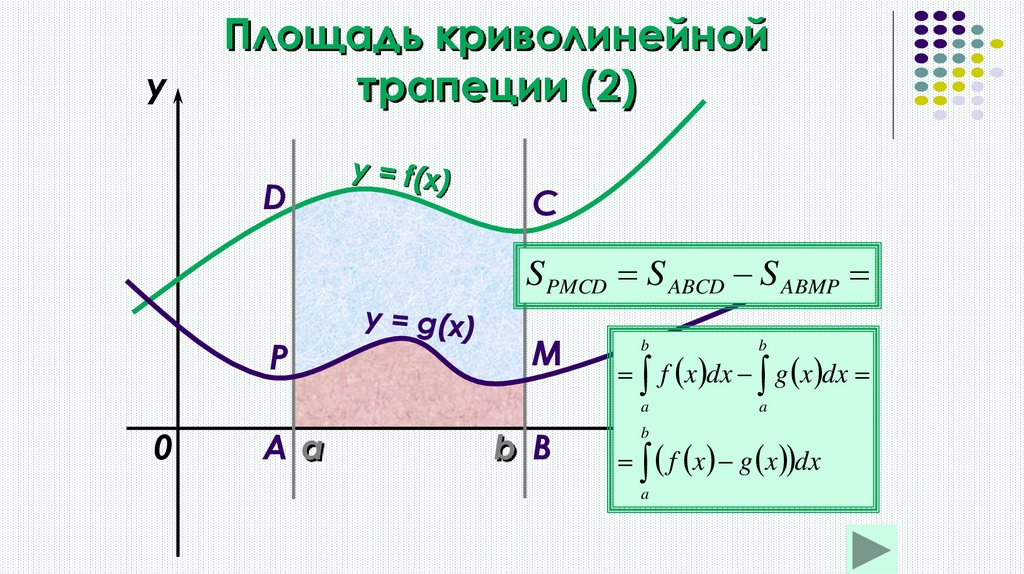
Площадь криволинейной трапеции (4)
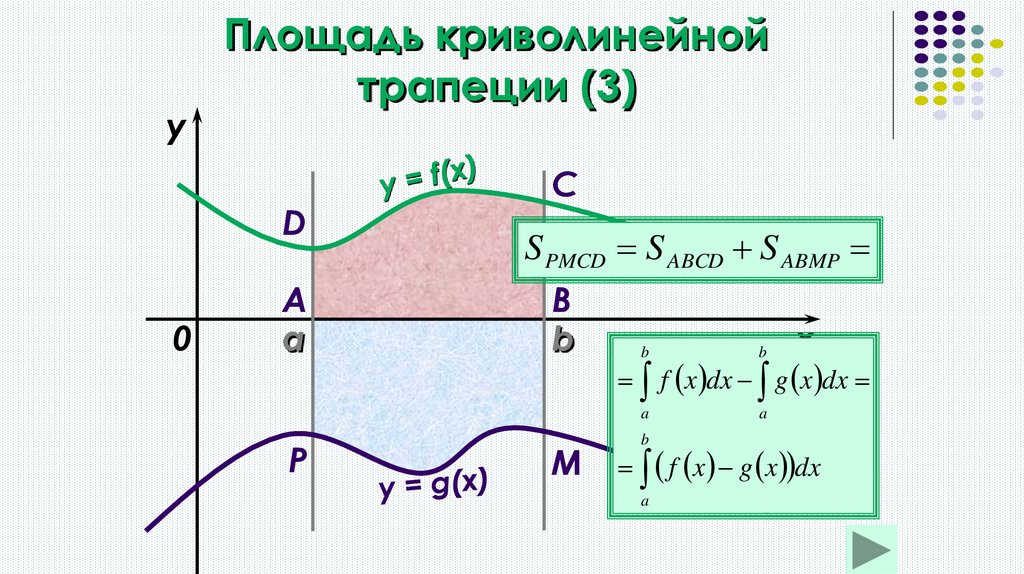
Пример (1)
Пример (2)

3. Понятие первообразной

Функцию F(x) называют первообразной для
функции f(x) на интервале (a; b), если на нем
производная функции F(x) равна f(x):
F ( x ) f ( x )
Операцию, обратную дифференцированию
называют интегрированием.

4.

Примеры
1. f(x) = 2x; F(x) = x2
F (x)= (x2) = 2x = f(x)
2. f(x) = – sin x; F(x) = сos x
F (x)= (cos x) = – sin x = f(x)
3. f(x) = 6x2 + 4; F(x) = 2x3 + 4x
F (x)= (2x3 + 4x) = 6x2 + 4 = f(x)
4. f(x) = 1/cos2 x; F(x) = tg x
F (x)= (tg x) = 1/cos2 x= f(x)

5. Неопределенный интеграл

Неопределенным интегралом от непрерывной
на интервале (a; b) функции f(x) называют
любую ее первообразную функцию.
f
(
x
)
dx
F
(
x
)
c
Где С – произвольная постоянная (const).

6.

Примеры
1. Adx Ax C ; Ax C A
2. e dx e С;
x
x
x
4. x dx
С;
4
3
x
cos x C sin x
3. sin xdx cos x С ;
4
e C e
x
x
1
С 4x 3 x 3
4
4
1
5.
dx tg x C ;
2
cos x
4
tg x C
1
2
cos x

7. Таблица первообразных

F(x)
x n 1
C
n 1
2x x
C
3
sin x C
cos x C
tgx C
ctgx C
F(x)
f(x)
x
a C
ax
lna
х
1
C
x
ln x
cos x
ex C
sin x
1
сos 2 x
1
sin2 x
C
ex
Cx
loga x C
1
x lna
f(x)
x
n
arcsin x C
1
1 x2

8.

Три правила нахождения
первообразных
1º Если F(x) есть первообразная для f(x), а G(x) –
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).
2º Если F(x) есть первообразная для f(x), а k –
постоянная, то функция kF(x) есть первообразная
для kf(х).
3º Если F(x) есть первообразная для f(x), а k и b –
1
постоянные, причем k ≠ 0, то функция
F(kx + b)
k
есть первообразная для f(kx + b).

9. Определенный интеграл

b
f x dx F x F b F a
b
a
a
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла
заключается в том, что определенный интеграл
равен
площади
криволинейной
трапеции,
образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.

10. Вычисление определенного интеграла

3x 2 x 1 dx x x x
2
2
3
2
2
1
1
23 22 2 13 12 1 6 1 5
10
3
2 x 6 x 6
x 6 dx
3
3
10
2 10 6 10 6 2 3 6 3 6 80
2
18 7
3
3
3
3

11. Площадь криволинейной трапеции

y
D
C
b
S ABCD f x dx
a
a
b
B
x=b
x=a
0
A
F b F a
y=0
x

12. Площадь криволинейной трапеции (1)

y
B
b
y=0
x
b
S ABCD f x dx
D
C
x=b
a
x=a
0
A
a
F a F b

13.

y
Площадь криволинейной
трапеции (2)
D
C
S PMCD S ABCD S ABMP
P
0
Aa
M
b B
b
b
a
a
f x dx g x dx
f x g x dxx
b
a

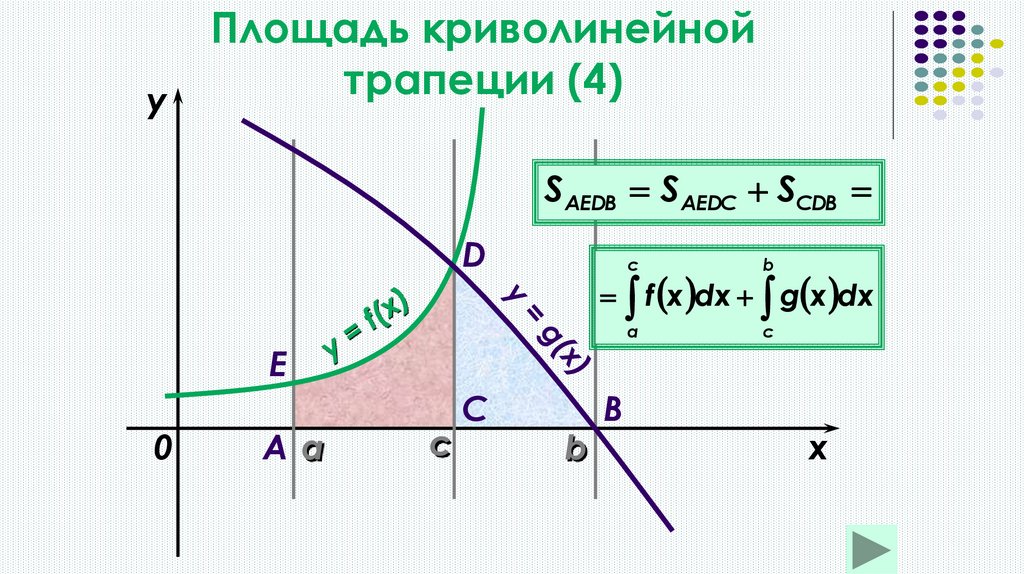
14.

y
Площадь криволинейной
трапеции (3)
D
0
A
a
P
C
S PMCD S ABCD S ABMP
B
b
M
b
b
a
a
x
f x dx g x dx
b
f x g x dx
a

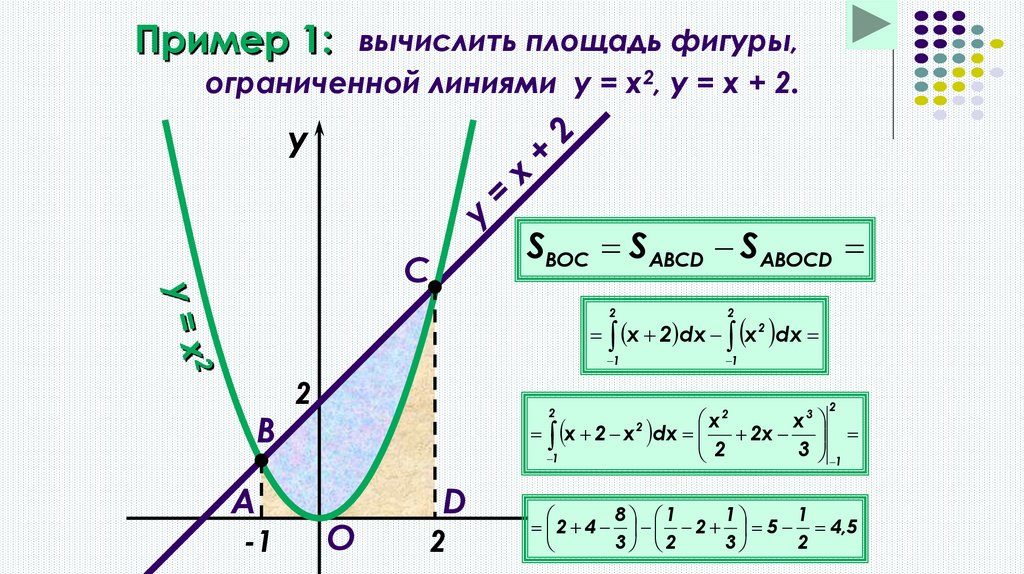
15. Пример 1:

вычислить площадь фигуры,
ограниченной линиями y = x2, y = x + 2.
y
SВОС SABCD SABOCD
C
2
2
1
1
x 2 dx x 2 dx
B
A
-1
2
2
2
x
x
х 2 х 2 dx 2x
3 1
2
1
O
D
2
2
3
8 1
1
1
2 4 2 5 4,5
3 2
3
2
x

16.

y
Площадь криволинейной
трапеции (4)
SАЕDВ SAEDC SСDB
D
с
b
a
с
f x dx g x dx
Е
0
Aa
с
C
b
B
x

17.

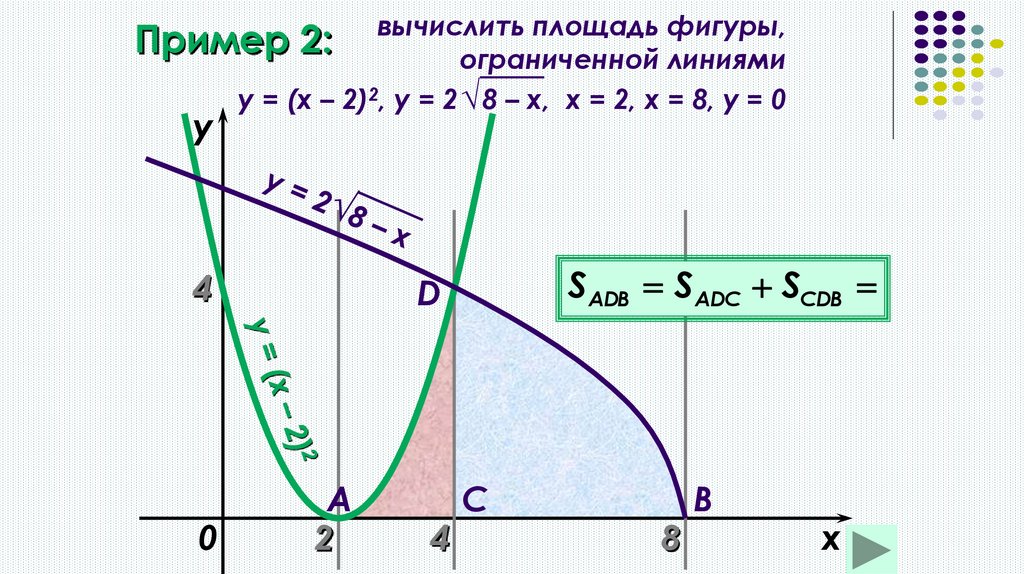
вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
y
4
0
SАDВ SADС SСDB
D
A
2
4
C
8
B
x

18.

вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
3 4
x 2
x - 2 dx 2 8 - хdx
4
2
2
8
4
3
8
4 8 x 8 x
3
2
4
4 2 3 2 2 3 4 8 8 8 8 4 8 4 8 4
3
3
3
3
8 32 40
1
13
3 3
3
3

19. СУТЬ МЕТОДА ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ

Этот метод основан на правиле
дифференцирования произведения
Пусть u = u(x), v = v(x) – функции, дифференцируемые на
некотором
промежутке
Х.
Тогда,
как
известно,
дифференциал произведения этих функций вычисляется по
формуле:
d(u·v)=u´dv + v´du
Взяв неопределенный интеграл от обеих частей этого
равенства, получим:
ʃd(u·v)=ʃ(udv + vdu)

20.

СУТЬ МЕТОДА ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ
Но ʃd(u·v) = u·v + C,
a ʃ(udv + vdu) = ʃudv + ʃvdu;
поэтому
u·v + C = ʃudv + ʃvdu,
откуда получаем:
ʃudv = uv + C - ʃvdu.

21.

СУТЬ МЕТОДА ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ
Так как ʃv´du уже содержит произвольную постоянную, то в
правой части полученного равенства можно опустить С и
записать равенство в виде:
ʃudv = uv - ʃvdu
(1).
Эта формула называется
формулой интегрирования по частям.
Ею обычно пользуются в тех случаях, когда подынтегральное
выражение v´du проще, чем подынтегральное выражение
u´dv.

22.

СУТЬ МЕТОДА ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ
Важно!!!
Одно и то же подынтегральное выражение можно записать
в виде udv различными способами.
Обычно стараются в подынтегральном выражении выделить
части u и dv так, чтобы функция v была не сложнее, чем v', а u'
проще, чем u.
В частности, полезно иметь в виду, что для таких функций, как
lnx, xⁿ, arctgx, arcctgx производные имеют более простой вид,
нежели сами функции. Поэтому в большинстве случаев эти
функции удобно принимать за u.

23.

ПРИМЕР 1. Вычислите
Табличного интеграла логарифмической функции нет, следовательно
другого пути нет, как принять его за u.
u ln x
dv x 3 dx
4
4
4
4
x
x
dx
x
1
x
1 4
3
3
x
3
х ln xdx v x dx 4 ln x 4 x 4 ln x 4 x dx 4 ln x 16 x C
4
4
du
dx
x

24.

ПРИМЕР 2. Вычислите
Производная степенной функции понижает показатель степени на 1,
поэтому удобнее ее взять за u.
u x2
du 2 xdx
2
x sin xdx dv sin xdx
v sin xdx cos x
u x
du dx
x 2 cos x 2 x cos xdx
dv cos xdx
v cos xdx sin x
x 2 cos x 2( x sin x sin xdx) x 2 cos x 2 x sin x 2 cos x C

25.

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
МЕТОДОМ ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ
Теорема.
Если функции u = u(x) и v = v(x) дифференцируемы на
отрезке [a; b], то имеет место формула
b
b
a
a
b
u
dv
uv
a v du

26.

e
x
ln
x
dx
ПРИМЕР 3. Вычислите
1
2
u ln x
x
1
x
e
x
ln
x
dx
ln
x
dx
1
1
2
21 x
du dx
x
e
2
e
dv x dx
x2
v
2
e
x2
1
e
ln x 1 x dx
2
21
2
2
2
2
2
e
1
e
1
e
e
1
1
e
x
x e ln e ln 1
e
ln x 1
2
4 4 2 4 4
1
2
4
2
4
2
2

27.

ПРИМЕР 4. Вычислите e sin x dx
x
0
u e x
dv sin x dx
e sin x dx e cos x 0 e cos x dx
x
du
e
dx
v
cos
x
0
0
x
x
x
u e x
dv cos x dx
e cos x 0 e sin x 0 e sin x dx
x
du
e
dx
v
sin
x
0
x
x
x
Пусть F ( x) e x sin x dx Тогда F ( x) e cos x 0 e sin x 0 F ( x)
x
0
x
2 F ( x) e x cos x 0 e x sin x 0
2 F ( x) e0 cos 0 e cos e sin e0 sin 0 1 e
1 e
F ( x)
2
Ответ:
1 e
0 e sin x dx 2
x

28.

КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. В чем смысл метода интегрирования по частям?
2. Запишите формулу интегрирования по частям.
3. Вычислите интегралы:
1) x cos x dx ;
x dx
2
2
2)
;
3
)
x
a
dx .
2
sin x
4. Сформулируйте теорему о вычислении определенных интегралов методом
интегрирования по частям.
5. Разберите и запишите примеры вычисления определенных интегралов в
презентации.
7. Вычислите определенные интегралы: