Чисельні методи

1.

Чисельні методи – це математичний інструментарій, за допомогою якого
математична задача формулюється у вигляді, зручному для розв’язання на комп’ютері.
Тоді математичну задачу називають обчислювальною задачею. Більшість чисельних
методів є наближеними методами розв’язання задачі, які дають змогу знайти
наближений до точного розв’язок з деякою похибкою.
За своєю структурою чисельнi методи дiляться на два типи: прямi та iтерацiйнi.
Означення 1. Чисельний метод називається прямим , якщо розв’язок досягається
через скiнченну кiлькiсть математичних дiй.
Прямими, наприклад, є методи Крамера та Жордана-Ґауса розв’язання систем
лiнiйних алгебраїчних рiвнянь
Означення 1. Чисельний метод називається iтерацiйним, якщо в ньому
виконується певна кiлькiсть iтерацiй (повторень однакових дiй) для отримання
наближеного розв’язку з заданою точнiстю.

2.

Основні поняття теорії похибок
Під час розв’язування прикладних задач важливо мати уяву про точність
одержаних результатів. Похибки, які виникають у таких результатах, зумовлені
наступними причинами:
• математичний опис задачі є неточним внаслідок неточності задання числових
даних або через невідповідність математичного опису задачі реальності;
• для розв’язування задачі використовують наближені методи;
• при вводі даних, під час виконання арифметичних операцій та виводу результатів
обчислень здійснюють округлення.
Похибки, викликані цими причинами, називають, відповідно:
• неусунена похибка;
• похибка методу;
похибка обчислень.

3.

Неусунену похибку часто класифікують як:
a) неусунену похибку обчислень, що є наслідком неточності задання параметрів
математичної моделі задачі;
b) b) похибку математичного моделювання, що є наслідком заміни реальної задачі її
математичною моделлю.
Розрізняють пряму та обернену задачу теорії похибок. Пряма задача полягає
у оцінюванні похибки результату обчислень, якщо відомі оцінки похибок вхідних
даних. Обернена задача полягає у визначенні необхідної точності вхідних даних,
що забезпечує задану точність результату обчислень.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

Приклад .Визначити абсолютну і відносну похибки наближеного числа.
Визначити, яка рівність більш точна.
9/11 = 0,818: √ 18=4,24
Розв`язок..
Знаходимо значення цих виразів із великою кількістю знаків
a=9/11 = 0,818181….. b= √ 18 = 4,2426…..
Потім обчислюємо граничні абсолютні похибки, закруглюючи їх з
перевищенням

26.

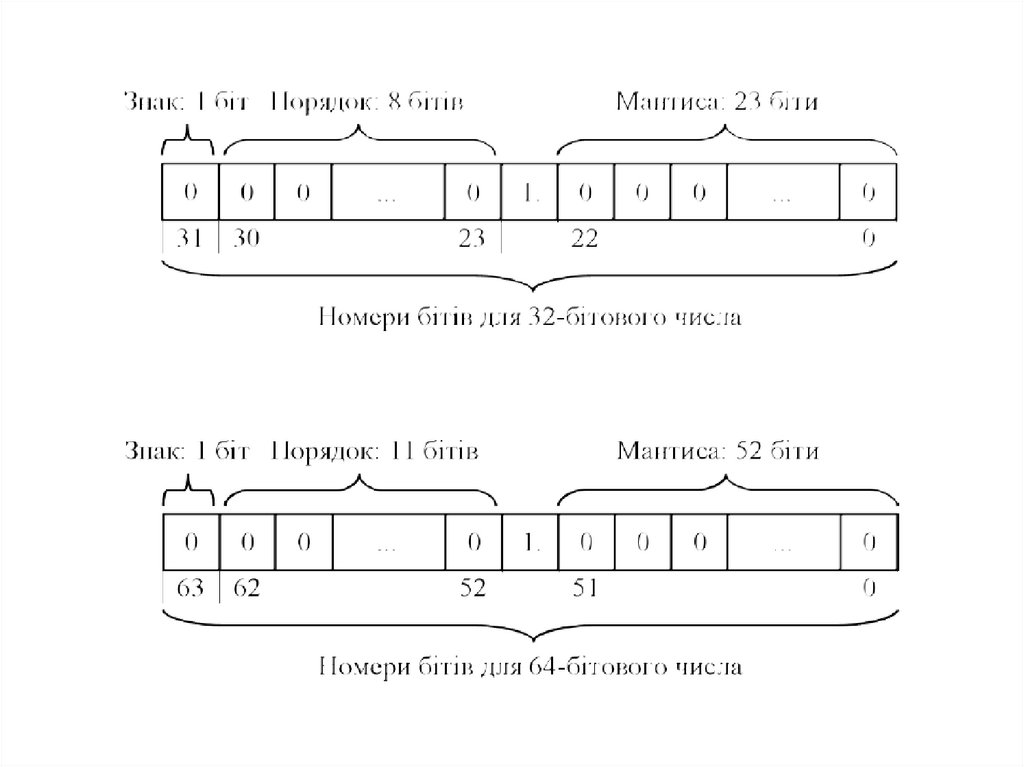
Похибка округлення в арифметицi з плаваючою крапкою
Розглянемо, як виникають погрiшностi округлень при розрахунках на комп’ютерi. Як
правило, всi числа у будь-якiй мовi програмування та на процесорному рiвнi
подаються як числа з плаваючою крапкою: