Чисельні методи. Лекція 1

1.

2.

• Лекція 1
• Математичні моделі
• Точність наближених обчислень
• Похибка методу.
• Похибка округлення
• Прямі та ітераційні методи
2

3.

• Для розв'язання математичних задач в основному
існує дві групи методів:
1. Аналітичні методи, в яких розв'язок задачі
подається у вигляді аналітичних виразів.
• Їх перевагами є: запис розв'язку у загальному
вигляді; висока точність і малий об'єм комп'ютерної
пам'яті для зберігання розв'язку.
• Основний недолік – неуніверсальність, бо тільки
невелика частина математичних задач може бути
розв'язана аналітично.
3

4.

• 2. Чисельні методи, що дозволяють звести розв'язування
задачі до виконання скінченного числа арифметичних і
логічних дій з числами. При цьому розв'язок визначається
як набір чисел, які надалі можуть бути інтерпретовані
різним способом (наприклад, подані у вигляді таблиць,
графіків, анімації тощо).
• Їх перевагами є: абсолютна універсальність, бо теоретично можуть бути застосовані для розв'язання будь-яких
задач; добре пристосовані для реалізації на комп'ютері.
• Недоліком є велика трудомісткість у ході ручного рахунку,
що, зазвичай, не є проблемою,
4

5.

• Чим ми з вами будемо займатися?
• Розглянемо два рівняння
2 x 1 0;
x 7 x cos5 x ln( x 4 1) 8
• Якщо з розв'язком першого них ніяких проблем бути
не може, то при розв'язку другого рівняння виникають
чималі труднощі.
• Аналогічна ситуація з обчисленням інтегралів
1
xdx ;
0
x x ln( x 1) 3
1 5
0
1 cos x
2
dx
5

6.

• Задачею обчислювальної математики є одержання
наближених чисельних рішень, коли це неможливо зробити
аналітичними методами, або ж коли використання
аналітичних методів є надто складним та трудомістким.
• При рішенні складних задач звичайно доводиться
застосовувати декілька методів. Так на початкових
(допоміжних) етапах це може бути чисельне
диференціювання, інтегрування, визначення власних
значень матриць, а на заключному розв’язок системи
лінійних алгебраїчних рівнянь(СЛАР). Тому ефективність
рішення задачі в цілому повністю визначається
характеристиками методів, що використовуються для
кожної складової.
6

7.

• Звичайно від методів потребують виконання
наступних вимог точність, стійкість, економічність та
універсальність.
• Кількісною мірою точності є величина похибки, яка за
своєю природою поділяється на
• - таку, що не можна усунути;
• - обчислювальну похибку.
7

8.

• Модель це деякий гнесеологічний об'єкт (що
відноситься до процесу пізнання), створений з метою
отримання та зберігання інформації про деякий
об'єкт-оригіналі. Будь-яка модель включає такі
компоненти.
• Об'єкт дослідження.
• Суб'єкт дослідження.
• Завдання, що стоїть перед дослідником.
• Засоби створення моделі.
8

9.

• На запитання є наступна математична конструкція
A
d 2 x(t )
dt 2
dx(t )
B
Cx(t ) f (t )
dt
• моделлю ми змушені відповісти НІ.
• Якщо прийняти A RC, B LC
• де R, L,C є відповідно електричним опором,
індуктивністю і ємністю, то отримуємо математичну
модель ділянки лінійного електричного ланцюга.
9

10.

• У випадку коли A m, B
• цей вираз є математичною моделлю руху
матеріальної точки масою m підвішеною на пружині
жорсткістю C з урахуванням сил опору.
• На перший погляд це дуже різні фізичні процеси,
• але спільним у них є те, що вони описують явище
коливань.
10

11.

• При чисельному розв’язку математичних і
прикладних задач на тому або іншому етапі майже
неминуче виникають похибки. Похибкою називається
відхилення наближеного розв’язку від істинного
розв’язку.
11

12.

• Кількісною мірою точності є величина похибки, яка за
своєю природою поділяється на
• - таку, що не можна усунути;
• - обчислювальну похибку.
• У першому випадку похибка виникає в результаті тих
спрощень, які приймались при побудові моделі, а
також з-за неточного дання параметрів моделі.
Вона не може змінитися в процесі рішення моделі,
але знати її необхідно щоб не назначати надмірно
жорсткі умови на точність.
12

13.

• Так у відомому з фізики рівнянні коливанні
матеріальної точки
d 2x
dx
m 2 cx 0 (1)
dt
dt
• де m– маса точки, – коефіцієнт опору, а c –
жорсткість пружини, параметри m, , c визначаються
шляхом вимірювання і мають похибку обумовлену
точністю вимірювальних приладів.
13

14.

• Якщо врахувати, що сила опору і жорсткість пружини є
нелінійними функціями відповідно швидкості і зміщення то
маємо рівняння
d 2x
2
3
dx
dx
dx
m 2 1 2 3 ... c1 x c2 x 2 c3 x 3 ... 0
dt
dt
dt
dt
• яке більш точно описує процес коливань. Похибка метода
виникає тому, що чисельними методом рішається друга,
більш проста задача, яка є наближенням вихідної. Так
рівняння (1) є наближенням рівняння (2). Процес заміни
нелінійної задачі лінійною називається лінеаризацією,
тобто (1) отримане шляхом лінеаризації останнього
рівняння.
14

15.

• Обчислювальну похибку поділяють на похибку методу
і похибку округлення.
• Причиною виникнення похибки метода є наближена
заміна об’єкту, що має нескінченне число вимірів ,
об’єктом з скінченним числом вимірів.
• Приклад 1. Наближена заміна відрізка x [a; b] скінченною множиною дискретних точок(дискретизація )
.
b a
xi a ih
h
N
15

16.

• Приклад 2. Якщо розв'язок деякої задачі функція f(x)
шукається у вигляді ряду
f ( x) i i ( x)
i 0
• То звичайно верхня границя сумування не може
дорівнювати нескінченності і замінюється деяким
цілим числом (не обовязково дуже великим)
N
f ( x) i i ( x)
i 0
16

17.

• Якщо похибка метода є його індивідуальною
характеристикою, то похибка округлення за своєю
природою визначається машинною формою
зображення числа. Так у системі з плаваючою
крапкою число зображується у вигляді
x q
p
t
k q k
k 1
17

18.

• тут q - ціле-основа системи числення; 1 ,.., t - цілі в
межах 0 k q . Довжина мантиси t визначається
числом розрядів і є величиною обмеженою t t 0 .
Очевидно, що при виконанні арифметичних дій,
довжина мантиси результату буде більше ніж t0 , і її
частина починаючи з t 1 повинна бути відкинутою.
Граничне значення t0 визначається як типом ЕОМ,
так і вимогами до системи зображення числа :
звичайна точність, подвійна і т.д.
18

19.

• На перший погляд здається , що чим детальніше буде
проведено розбиття відрізка, тим похибка результату
буде менша. Але це справедливо тільки для похибки
метода. Зі збільшенням точок зростає обсяг
обчислень і значить і похибка округлення.
19

20.

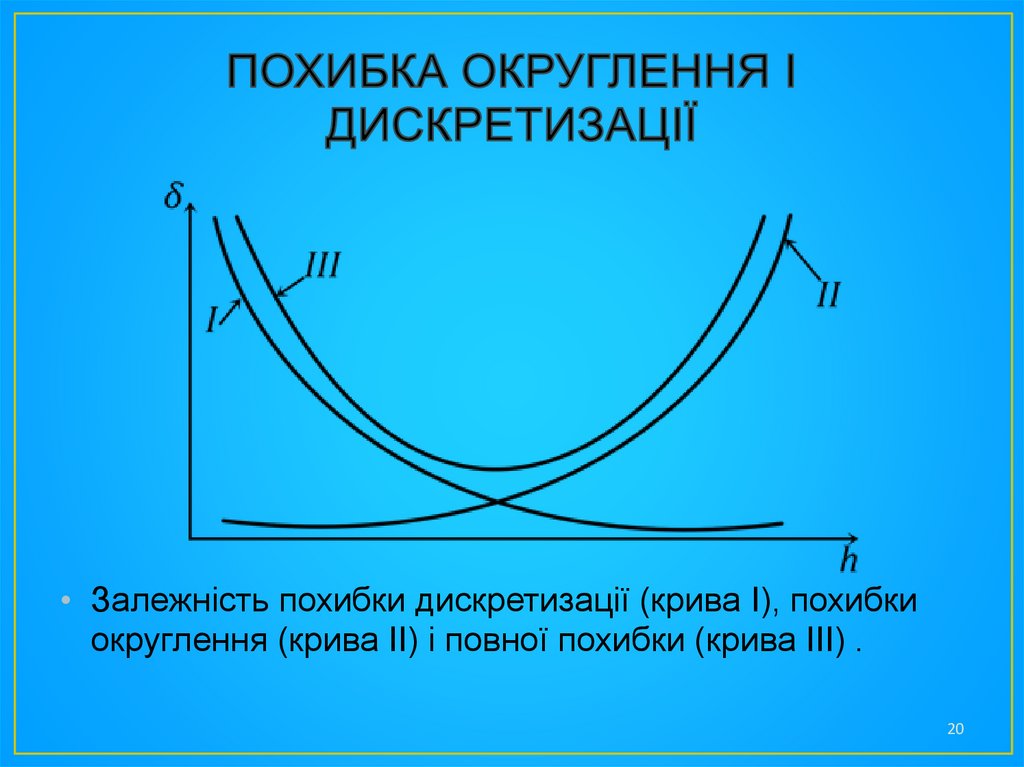
• Залежність похибки дискретизації (крива I), похибки
округлення (крива II) і повної похибки (крива III) .
20

21.

• Розглянемо один випадок прояву обчислювальної
похибки. Якщо при розв’язанні рівняння
x 2 140 x 1 0
• обчислення проводити в десятинній системі числення,
при цьому в мантисі числа після округлення
отримувати чотири розряду, то
• x 70 4899 , 4899 69.9992...
• і після округлення маємо
x 70 69,99 0,01
21

22.

• Якщо те саме значення x знайти позбувшись
ірраціональності
x 70 4899
4899 4900 4899
1
70
0,007148
70 69,99 139,9
70 4899
• Провівши обчислювання з додатковими розрядами,
можна, перевірити, що в обох випадках всі
підкресленні цифри вірні, але в другому випадку
точність результату суттєво вище. Справа у тому що у
першому випадку прийшлось віднімати два близькі
великі числа. Цей ефект має назву втрати
значущих цифр при відмінні.
22

23.

• Вважається, що метод є стійким, якщо невеликі зміни
вхідних параметрів приводять до невеликих змін в
результатах.
• Економічність методу визначається обсягом
обчислень необхідним для його реалізації. На
практиці пріоритетним є вимоги точності та стійкості.
Якщо виникає потреба вибору одного з кількох
методів, то при виконанні цих двох умов проводиться
порівняння за іншими характеристиками
23

24.

• Чисельні методи діляться на два класи прямі та
ітераційні. При застосуванні прямих методів алгоритм
рішення використовується один раз. Рішення задачі
ітераційним методом (методом послідовних
наближень) складається з наступних етапів:
• - вибір початкового наближення;
• - визначення нового наближення;
• - перевірка виконання умови зупинки алгоритму;
• - перехід до наступного наближення, якщо умова
зупинки не виконується.
24

25.

• Умовою зупинки може бути, як величина різниці між
двома наближеннями, так і кількість ітерацій.
Ітераційні методи застосовуються у тих випадках коли
використати прямі методи неможливо, або ж коли
відоме початкове наближення близьке до точного.
При використанні ітераційних методів суттєвим є
поняття збіжності. Якщо U ( n) U, при n де n номер наближення, а U - точне рішення, то метод
збігається.
25

26.

• Практичною мірою збіжності алгоритму є виконання
умови
( n 1)
( n)
(n)
( n 1)
U
U
U
U
• Величина норми обчислюється наступним чином:
• для числа U U
1
n
2
2
U ui
• для вектора
i 1
1
;
b
2
2
• для функції U ( x) U ( x)dx
.
a
26

27.

• Чисельний метод вважається вдало вибраним, якщо
його похибка в декілька разів менше, похибки, що не
усувається, а обчислювальна похибка в декілька разів
менша похибки метода.
27