Similar presentations:
Чисельні методи розв’язування систем лінійних алгебраїчних рівнянь
1.
2.
ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ (СЛАР).СЛАР (системи лінійних алгебраїчних рівнянь) найбільш прості, але в той же час до них
зводиться багато задач чисельного аналізу. Є багато різних способів розв’язку СЛАР.
Методи розв’язування СЛАР, які використовуються на практиці, можна
розділити на дві великі групи:
3.
Методи розв’язування СЛАР поділяються на прямі та ітераційні. Приумові точного виконання обчислень прямі методи за скінчену кількість операцій
в результаті дають точний розв’язок. Використовуються вони для невеликих та
середніх СЛАР n=100-10000 .
Ітераційні методи використовуються для великих СЛАР n>100000, як
правило розріджених. В результаті отримуємо послідовність наближень, яка
збігається до розв’язку.
4.
Методи послідовних наближень характеризуються тим, що з самого початкузадаються деякими наближеними значеннями невідомих. Із цих наближених значень
тим чи іншим способом отримують нові покращені наближені значення.
З новими наближеними значеннями поступають аналогічно.
При виконанні певних умов можна прийти, після великої кількості кроків, до
точного розв’язку.
Точні методи характеризуються тим, що з їх допомогою можливо, провівши
скінчене число операцій, одержати точні значення невідомих. При цьому
припускається, що коефіцієнти і праві частини системи відомі точно, а всі обчислення
здійснюються без заокруглень. Частіше вони здійснюються в два етапи:
на першому етапі перетворюють систему до того чи іншого простого виду;
на другому – розв’язують спрощену систему і отримують значення невідомих.
Найпростішим з точних методів являється метод виключення Гаусса.
5.
Метод виключення ГауссаМетод Гаусса був запропонований відомим німецьким математиком
Карлом Фрідріхом Гауссом (1777 - 1855) і є одним з найбільш універсальних
методів вирішення СЛАР.
Карл Фрідріх Гаус - німецький математик, засновник однойменного методу рішення СЛАР
Карл Фрідріх Гаус - був відомим великим математиком і його свого часу
визнали «королем математики». Хоча назва «метод Гаусса» є загальноприйнятим,
Гаусс не є його автором: метод Гаусса був відомий задовго до нього. Перше його опис
є в китайському трактаті «Математика в дев'яти книгах», який складений між II ст. до
н. е. і I ст. н. е. і являє собою компіляцію попередніх праць, написаних приблизно в X
ст. до н. е.
6.
Сутність цього методу полягає в тому, що за допомогою послідовнихвиключень невідомих дана система перетворюється на ступінчасту (зокрема,
трикутну) систему, рівносильну даній. При практичному вирішенні завдання,
розширена матриця системи за допомогою елементарних перетворень над її
рядками зводиться до ступінчастого вигляду. Далі послідовно знаходяться всі
невідомі, починаючи від низу до верху.
Тобто метод Гаусса - найбільш універсальний метод для знаходження
рішення будь-якої системи лінійних рівнянь, він працює в разі, коли система має
нескінченно багато рішень або несумісна.
7.
СЛАР в залежності від її елементів може мати:1. Одне рішення;
2. багато рішень;
3. зовсім не мати рішень.
У перших двох випадках СЛАР називається сумісною, а в третьому випадку несумісна. Якщо система має одне рішення, вона називається визначеною., а якщо
рішень більше одного, тоді система називається невизначеною.
До елементарним перетворенням відносяться:
• зміна місць рівнянь системи;
• почленное множення обох частин на одне з рівнянь на деяке число, так, щоб
коефіцієнти при першій змінної в двох рівняннях були протилежними числами;
• складання до обох частин одного з рівнянь певних частин іншого рівняння.
8.
Якщо з системою рівнянь провести такі дії:• множити обидві частини кожного з рівнянь на довільне і відмінне від нуля число;
• міняти місцями рівняння;
• до обох частин будь-якого з рівнянь додати певні частини іншого рівняння, які
множаться на довільне число,тоді виходить еквівалентна система, у якій таке ж
рішення чи нема рішень зовсім.
Метод Гаусс складається з двух етапiв: прямий хiд, зворотний хiд .
Нехай дана довільна СЛАР (1):
(1)
9.
Прямий хiд мiстить у собi n−1 крокiв.Крок 1
10.
(2)11.
Крок 2.12.
13.
Подальшi кроки такi самi.14.
(3)15.
16.
(4)17.
18.
19.
20.
Приклад 1. Вирішити систему рівнянь методом Гаусса.3 x1 x2 5,
2 x1 x2 x3 0,
2 x x 4 x 15.
1
2
3
Рішення: Прямий хід.
Розділимо перше рівняння на 3, отримаємо систему:
x 1 x 5 ,
1 3 2 3
2 x1 x 2 x3 0,
2 x x 4 x 15.
2
3
1
21.
Помножимо перше рівняння на 2 і складемо з другимрівнянням системи, отримаємо:
x 1 x 5 ,
1 3 2
3
10
1
x2 x3
,
3
3
2 x1 x2 4 x3 15.
Помножимо перше рівняння на -2 і складемо з третім
рівнянням системи, отримаємо:
22.
x 1 x 5 ,1 3 2 3
10
1
x2 x3 ,
3
3
35
1
3 x2 4 x3 3 .
Розділимо друге рівняння на 1/3, отримаємо:
1
5
x1 3 x2 3 ,
x2 3 x3 10,
1 x2 4 x3 35 .
3
3
23.
Помножимо друге рівняння на 1/3 і складемо з третімрівнянням системи, отримаємо:
1
5
x1 3 x 2 3 ,
x 2 3 x3 10,
5 x3 15.
Розділимо третє рівняння на 5, отримаємо:
1
5
x1 3 x 2 3 ,
x 2 3 x3 10,
x 3 3.
24.
Зворотній хід.З третього рівняння знаходимо
x3 3
З другого рівняння знаходимо
x2 10 3 3 1
З третьего рівняння знаходимо
5 1
x1 2
3 3
25.
26.
27.
Стiйкiсть методу. У математицi пiд стiйкiстю розв’язку розумiютьйого мале змiнювання при малому змiнюваннi вхiдних даних. У
чисельних методах, крiм погрiшностей у вхiдних даних,
виникають також погрiшностi пiд час розрахункiв.
Означення 1. Чисельний метод називається стiйким до
погрiшностей у вхiдних даних, якщо при малих погрiшностях у
вхiдних даних вiн дає малу погрiшнiсть у результатi обчислень.
Означення 2. Чисельний метод називається стiйким до
погрiшностей обчислень та округлень, якщо цi погрiшностi не
впливають не результат розрахункiв.














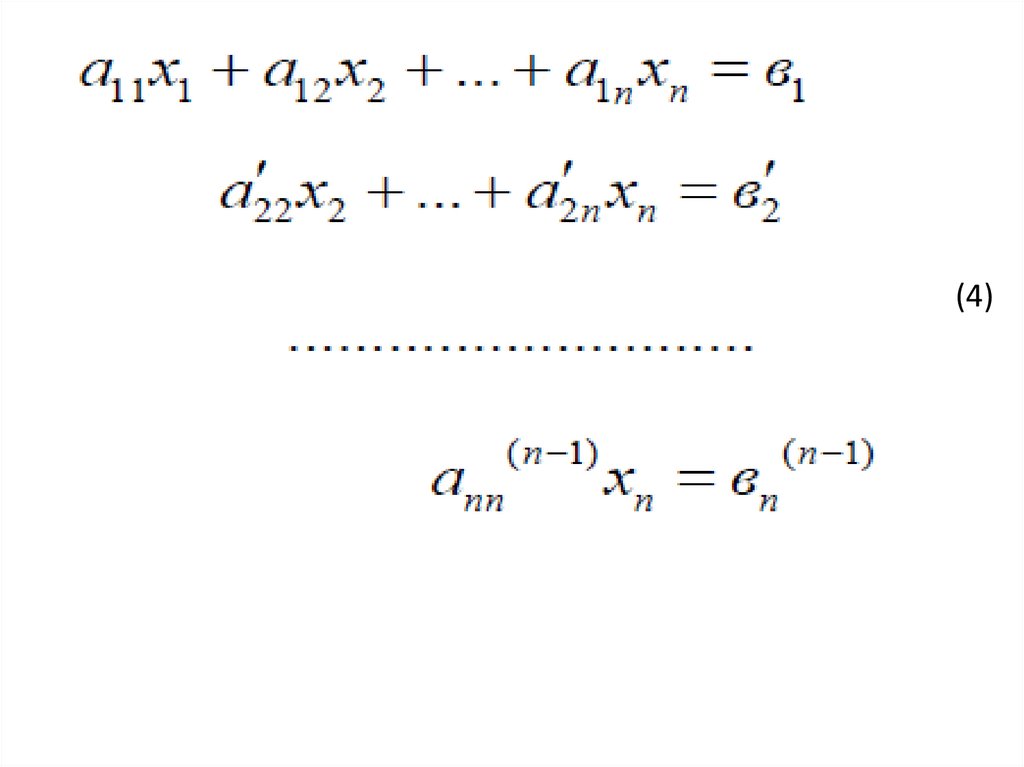
























 mathematics
mathematics








