Алгебра матриц. Виды матриц

1. Алгебра матриц

Овчинникова Е.В.

2. ВИДЫ МАТРИЦ

Матрицей A = (aij) размера m × n называется прямоугольная
таблица чисел, содержащая m строк и n столбцов:
Числа аij (i = 1...m; j = 1...n), составляющие данную матрицу,
называются ее элементами: i – номер строки матрицы, j – номер
столбца.
2

3. ВИДЫ МАТРИЦ

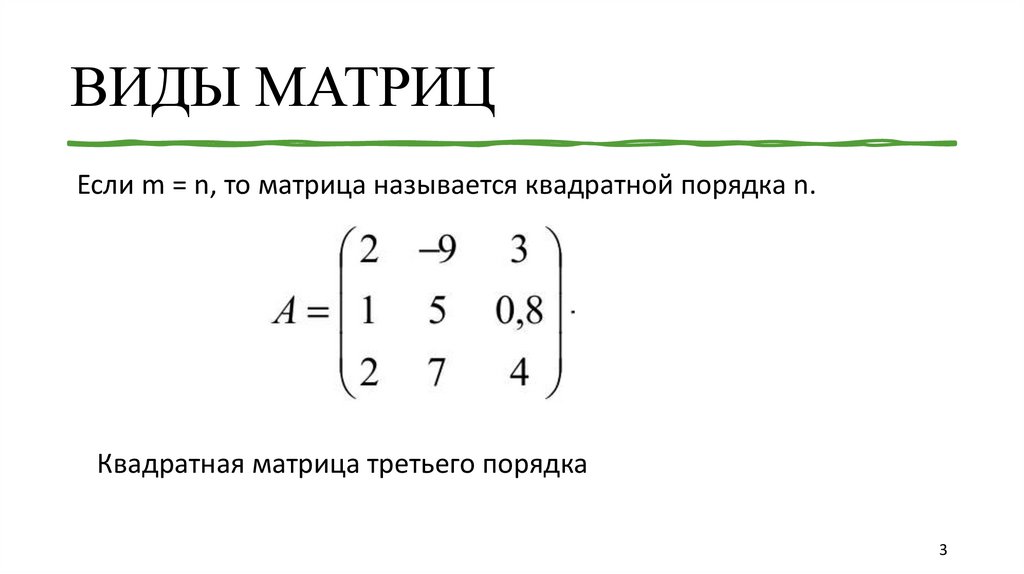
Если m = n, то матрица называется квадратной порядка n.
Квадратная матрица третьего порядка
3

4. ВИДЫ МАТРИЦ

Матрица, состоящая из одной строки, называется векторомстрокой, а матрица, со стоящая из одного столбца – векторомстолбцом.
A = (a a ,…, a1n) –вектор-строка;
11
12
–вектор-столбец
4

5. ВИДЫ МАТРИЦ

Элементы квадратной матрицы aij, у которых номер столбца равен номеру
строки (I = j), называются диагональными и образуют главную диагональ
матрицы. Если все внедиагональные элементы квадратной матрицы равны
нулю, то матрица называется диагональной.
5

6. ВИДЫ МАТРИЦ

Если у диагональной матрицы n-го порядка все диагональные элементы
равны единице, то матрица называется единичной матрицей n-го порядка,
она обозначается буквой E.
Единичная матрица третьего порядка
6

7. ВИДЫ МАТРИЦ

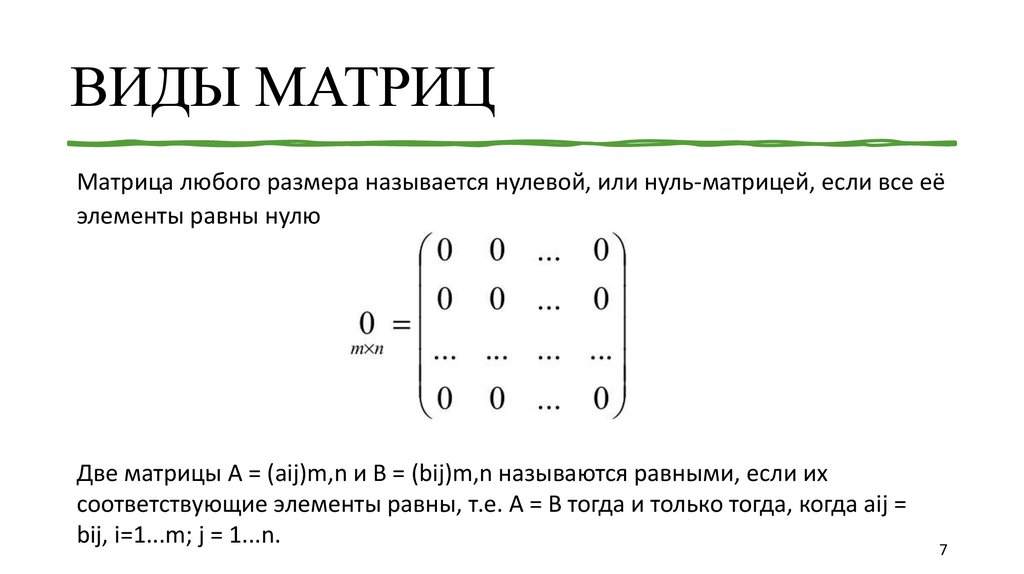
Матрица любого размера называется нулевой, или нуль-матрицей, если все её
элементы равны нулю
Две матрицы А = (аij)m,n и В = (bij)m,n называются равными, если их
соответствующие элементы равны, т.е. А = В тогда и только тогда, когда aij =
bij, i=1...m; j = 1...n.
7

8. ДЕЙСТВИЯ НАД МАТРИЦАМИ

Суммой двух матриц А = (аij)m,n и В = (bij)m,n называется матрица С = А + В,
элементы которой сij равны сумме соответствующих элементов аij и bij матриц
А и В.
Для суммы матриц справедливы следующие свойства:
1. А + В = В + А – коммутативность;
2. А + (В + С) = (А + В) + С – ассоциативность;
3. А + 0 = А, 0 – нулевая матрица.
8

9. ДЕЙСТВИЯ НАД МАТРИЦАМИ

Произведением матрицы А = (аij)m,n на число α называется матрица В = αА,
элементы которой bij вычисляются следующим образом: bij = αaij, i = 1...m; j =
1...n.
свойства:
9

10. ДЕЙСТВИЯ НАД МАТРИЦАМИ

Матрица (-А) = (-1) × А называется противоположной матрице А.
Разность двух матриц одинакового размера определяется через предыдущие операции:
A – B = A +(-1) × B.
10

11. ДЕЙСТВИЯ НАД МАТРИЦАМИ

Произведением матрицы А порядка m × k на матрицу В порядка k ×n (т.е. количество столбцов
первой матрицы равно числу строк второй) называется матрица С = А × В порядка m × n , элементы
которой сij вычисляются по формуле:
Из данного выражения следует правило умножения матриц: чтобы получить элемент, стоящий на
пересечении i-й строки и j-го столбца матрицы С, необходимо все элементы i-й строки матрицы А
умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения
сложить. Для произведения матриц справедливы следующие свойства:
11

12. ДЕЙСТВИЯ НАД МАТРИЦАМИ

Найти произведения АВ и ВА матриц
12

13. Транспонирование матрицы

такое преобразование, при котором строки заменяются
соответствующими столбцами. Обозначение транспонированной
матрицы: A′,