Четыре замечательные точки треугольника (11 класс)

1.

Муниципальное бюджетное общеобразовательное учреждение города Костромы
Средняя общеобразовательная школа №2
Четыре замечательные
точки треугольника»
Автор проекта:
Боков В.С.- учащийся
11А класса
Руководитель проекта:
Селезнева М.В
преподаватель
математики
Кострома, 2025

2.

⮚ 1. Введение
Содержание
⮚2. Исторические сведения о замечательных точках треугольника
⮚ 3.Треугольник
⮚ 4.Медианы треугольника
⮚5. Биссектрисы треугольника
⮚ 6.Высоты в треугольнике
⮚7. Исследование замечательных точек треугольника
⮚8.Заключение
⮚9.Список литературы
⮚
⮚

3.

Введение
Геометрия - это раздел математики, который рассматривает различные
фигуры и их свойства. Геометрия начинается с треугольника. Вот уже два с
половиной тысячелетия треугольник является символом геометрии; но он не
только символ, треугольник - атом геометрии.
В своей работе я рассмотрю свойства точек пересечения биссектрис, медиан
и высот треугольника, расскажу о замечательных их свойствах и линиях
треугольника.
К числу таких точек, относятся:
а) точка пересечения биссектрис (центр вписанной окружности);
б) точка пересечения серединных перпендикуляров (центр описанной
окружности);
в) точка пересечения высот (ортоцентр);
г) точка пересечения медиан (центроид).
Цель проекта:: исследование треугольника на его замечательные
точки, изучение их классификаций и свойств.

4.

1. Исторические сведения о замечательных точках треугольника
Свойства треугольника были хорошо изучены еще в древности греками. В знаменитых
«Началах» Евклида доказывается, что центром окружности, описанном около треугольника,
является точка пересечения серединных перпендикуляров к его сторонам.
Принято считать, что вся современная наука оформилась в 17 веке.
Начало открытий замечательных точек треугольника, положил в 17 веке Джованни Чева (1648 - 1734) –
итальянский математик. Основной заслугой Чевы является построение учения о секущих, которое
положило начало новой – синтетической геометрии; оно изложено в сочинении "О взаимно
пересекающихся прямых".
Во-первых, его теорема (знаменитая теорема Чевы) сама по себе представляет ценность, во-вторых, ее
применение позволило открыть свойства замечательных точек треугольника, известных как точки
Нагеля и Жергонна.

5.

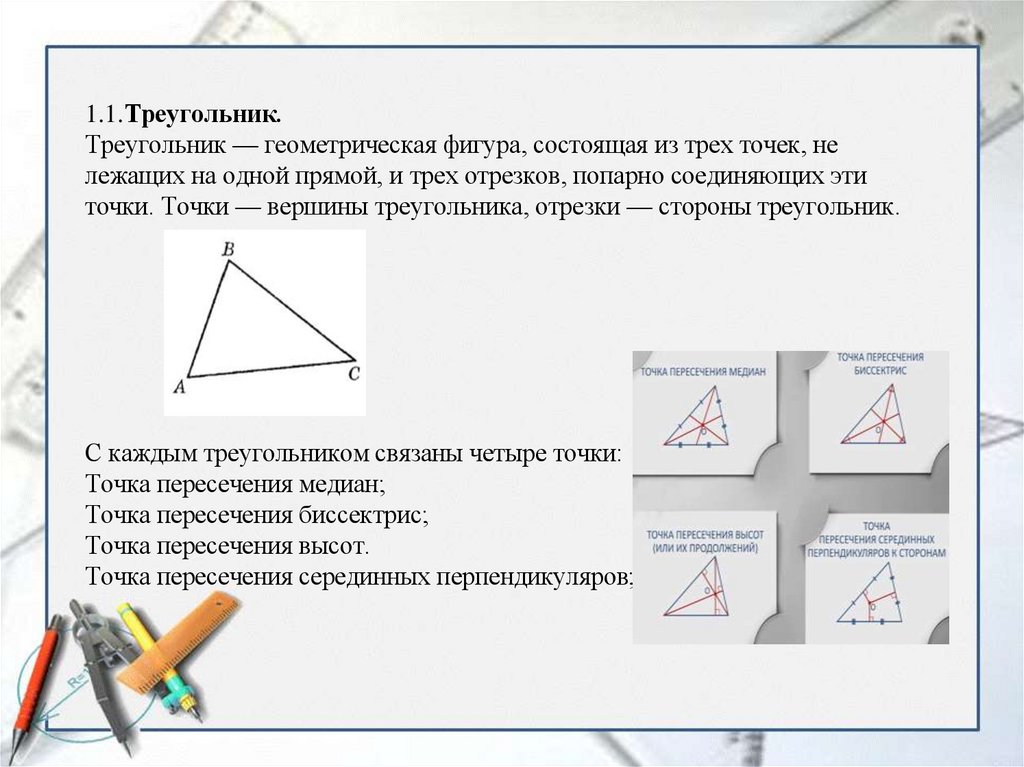
1.1.Треугольник.
Треугольник — геометрическая фигура, состоящая из трех точек, не
лежащих на одной прямой, и трех отрезков, попарно соединяющих эти
точки. Точки — вершины треугольника, отрезки — стороны треугольник.
С каждым треугольником связаны четыре точки:
Точка пересечения медиан;
Точка пересечения биссектрис;
Точка пересечения высот.
Точка пересечения серединных перпендикуляров;

6.

1.2. Медианы треугольника.
Медиана треугольника ― отрезок, соединяющий вершину треугольника с
серединой противоположной стороны. Точка пересечения медианы со стороной
треугольника называется основанием медианы.
Построим середины сторон треугольника и проведем отрезки, соединяющую
каждую из вершин с серединой противолежащей стороны. Такие отрезки
называются медианой.
Мы видим, что эти отрезки пересекаются в одной точке. Если мы измерим
длины получившихся отрезков медиан, то можно проверить еще одно свойство:
точка пересечения медиан делит все медианы в отношении 2:1, считая от вершин.
И еще, треугольник, который опирается на острие иглы в точке пересечения
медиан, находится в равновесии! Точка, обладающая таким свойством,
называется центром тяжести (барицентр). Центр равных масс иногда называют
центроидом.

7.

1.3.Биссектрисы треугольника.
Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный
от вершины угла до её пересечения с противолежащей стороной. У треугольника
существуют три биссектрисы, соответствующие трём его вершинам.
В произвольном треугольнике ABC проведем биссектрисы его углов. И вновь
при точном построении все три биссектрисы пересекаются в одной точке D.
Точка D – тоже необычная: она равноудалена от всех трех сторон треугольника. В
этом можно убедиться, если опустить перпендикуляры DA 1, DB 1 и DC1 на
стороны треугольника. Все они равны между собой: DA1=DB1=DC1.
Если провести окружность с центром в точке D и радиусом DA 1, то она будет
касаться всех трех сторон треугольника (то есть будет иметь с каждым из них
только одну общую точку). Такая окружность называется вписанной в
треугольник. Биссектрисы углов треугольника пересекаются в центре вписанной
окружности.

8.

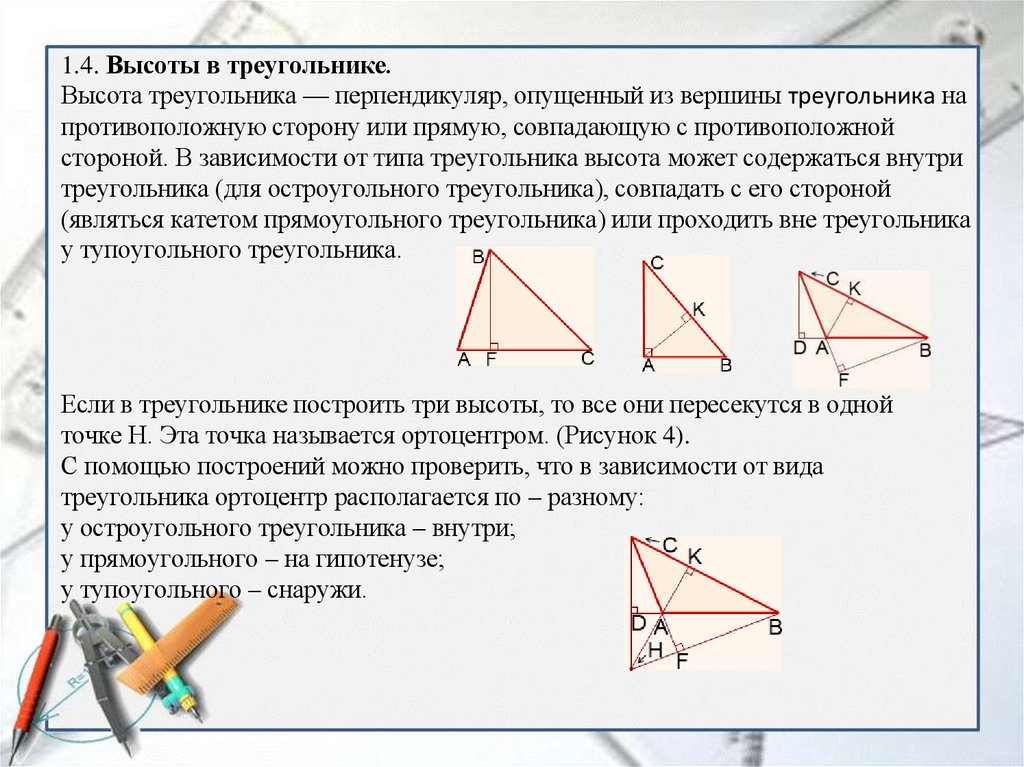
1.4. Высоты в треугольнике.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на
противоположную сторону или прямую, совпадающую с противоположной
стороной. В зависимости от типа треугольника высота может содержаться внутри
треугольника (для остроугольного треугольника), совпадать с его стороной
(являться катетом прямоугольного треугольника) или проходить вне треугольника
у тупоугольного треугольника.
Если в треугольнике построить три высоты, то все они пересекутся в одной
точке H. Эта точка называется ортоцентром. (Рисунок 4).
С помощью построений можно проверить, что в зависимости от вида
треугольника ортоцентр располагается по – разному:
у остроугольного треугольника – внутри;
у прямоугольного – на гипотенузе;
у тупоугольного – снаружи.

9.

1.5. Серединные перпендикуляры к сторонам треугольника
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному
отрезку и проходящая через его середину.
Начертим произвольный треугольник ABC и проведем серединные
перпендикуляры к его сторонам. Если построение выполнено точно, то все
перпендикуляры пересекаются в одной точке – точке О. Эта точка равноудалена от
всех вершин треугольника. Другими словами, если провести окружность с
центром в точке О, проходящую через одну из вершин треугольника, то она
пройдет и через две другие его вершины.
Окружность, проходящая через все вершины треугольника, называется описанной
около него. Поэтому установленное свойство треугольника можно
сформулировать так: серединные перпендикуляры к сторонам треугольника
пересекаются в центре описанной окружности.

10.

2. Исследование замечательных точек треугольника.
Все три высоты треугольника пересекаются в одной точке. Эта точка называется
ортоцентром треугольника.
Высоты остроугольного треугольника расположены строго внутри треугольника.
Соответственно, точка пересечения высот также находится внутри треугольника.
В прямоугольном треугольнике две высоты совпадают со сторонами. (Это высоты,
проведенные из вершин острых углов к катетам).
Высота, проведенная к гипотенузе, лежит внутри треугольника.
AC — высота, проведенная из вершины С к стороне AB.
AB — высота, проведенная из вершины B к стороне AC.
AK — высота, проведенная из вершины прямого угла А к гипотенузе ВС.
Высоты прямоугольного треугольника пересекаются в вершине прямого угла (А
— ортоцентр)..
В тупоугольном треугольника внутри треугольника лежит только одна высота —
та, которая проведена из вершины тупого угла.
.

11.

2. Исследование замечательных точек треугольника.
Все три высоты треугольника пересекаются в одной точке. Эта точка называется
ортоцентром треугольника.
Высоты остроугольного треугольника расположены строго внутри треугольника.
Соответственно, точка пересечения высот также находится внутри треугольника.
В прямоугольном треугольнике две высоты совпадают со сторонами. (Это высоты,
проведенные из вершин острых углов к катетам).
Высота, проведенная к гипотенузе, лежит внутри треугольника.
AC — высота, проведенная из вершины С к стороне AB.
AB — высота, проведенная из вершины B к стороне AC.
AK — высота, проведенная из вершины прямого угла А к гипотенузе ВС.
Высоты прямоугольного треугольника пересекаются в вершине прямого угла (А
— ортоцентр)..
В тупоугольном треугольника внутри треугольника лежит только одна высота —
та, которая проведена из вершины тупого угла.
.

12.

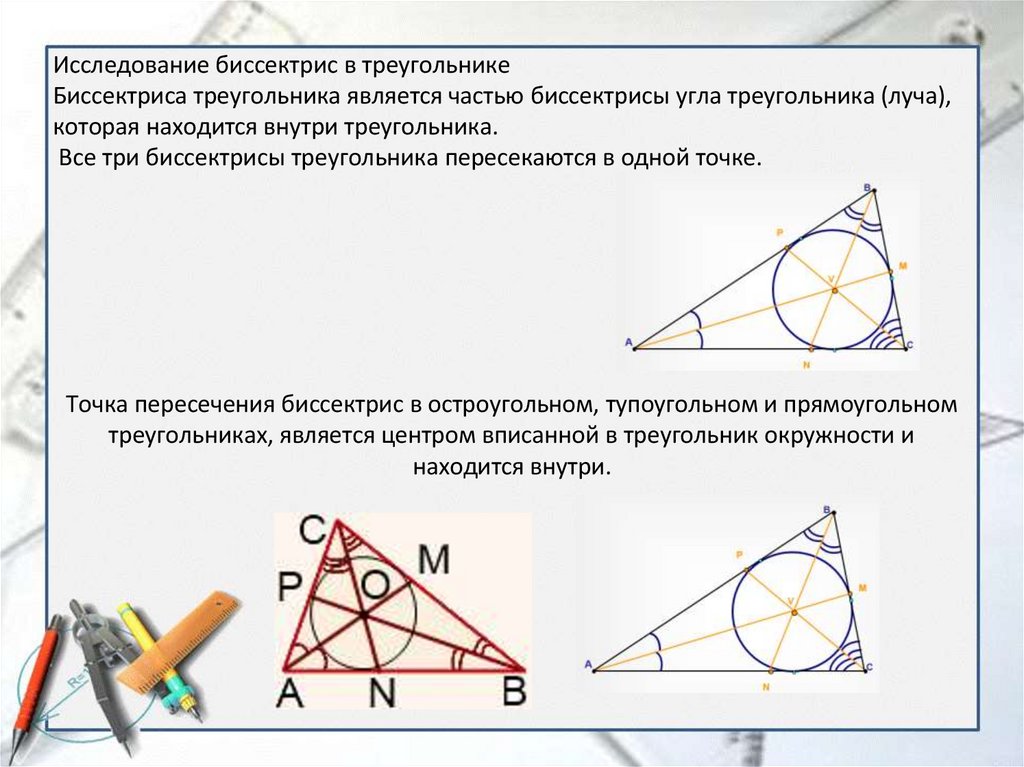
Исследование биссектрис в треугольнике
Биссектриса треугольника является частью биссектрисы угла треугольника (луча),
которая находится внутри треугольника.
Все три биссектрисы треугольника пересекаются в одной точке.
Точка пересечения биссектрис в остроугольном, тупоугольном и прямоугольном
треугольниках, является центром вписанной в треугольник окружности и
находится внутри.

13.

Исследование медиан в треугольнике.
Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих
вершину и середину противолежащей стороны, тоже три.
Исследовав я понял, что в любом треугольнике медианы пересекаются в одной
точке. Эту точку называют центром тяжести треугольника.
Исследование серединных перпендикуляров к стороне треугольника.
Серединный перпендикуляр треугольника – это перпендикуляр, проведенный к
середине стороны треугольника. Три серединных перпендикуляра треугольника
пересекаются в одной точке, являются центром описанной окружности.
Точка пересечения серединных перпендикуляров в остроугольном треугольнике
лежит внутри треугольника; в тупоугольном – вне треугольника; в прямоугольном
– на середине гипотенузы.

14.

Заключение
В ходе проделанной работы мы приходим к следующим выводам:
Цель достигнута: исследовали треугольник и нашли его замечательные точки.
Поставленные задачи решены:
1). Изучили необходимую литературу;
2). Изучили классификацию замечательных точек треугольника;
3). Научились строить замечательные точки треугольника;
Гипотеза, что умение находить замечательные точки треугольника, помогает в
решении задач на построение подтвердилась.
В работе последовательно излагаются приемы построения замечательных точек
треугольника, приведены исторические сведения о геометрических построениях.

15.

СПАСИБО
ЗА
ВНИМАНИЕ!