Центральные и вписанные углы

1.

2.

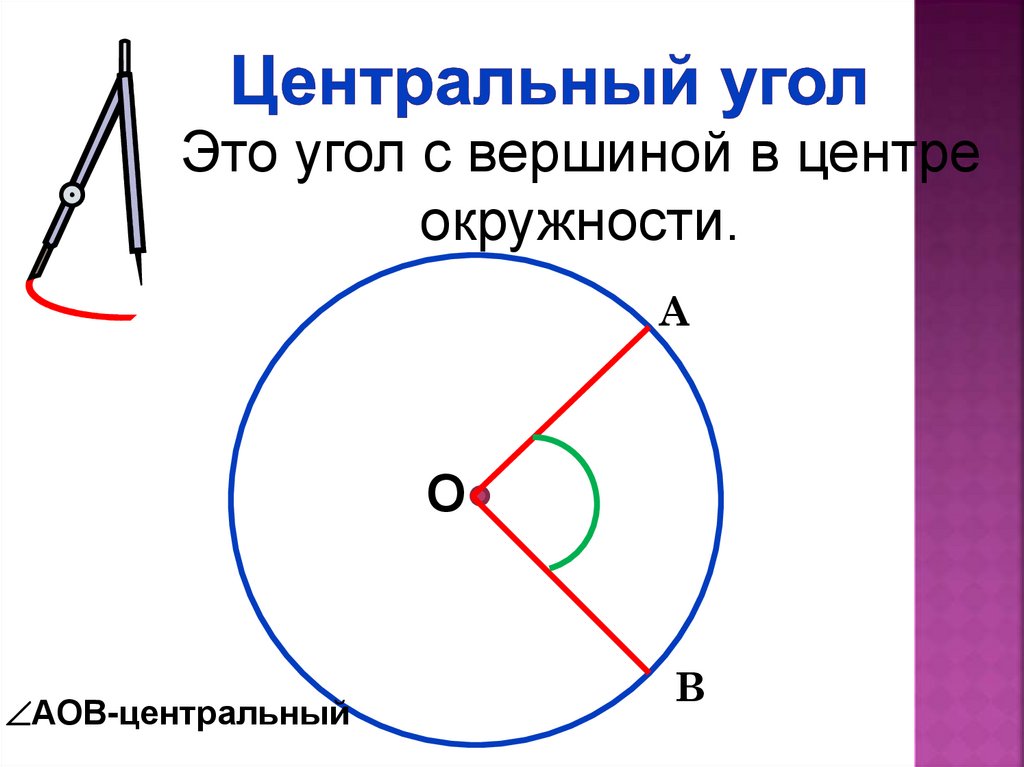
Это угол с вершиной в центре
окружности.
А
О
АОВ-центральный
В

3.

А
О
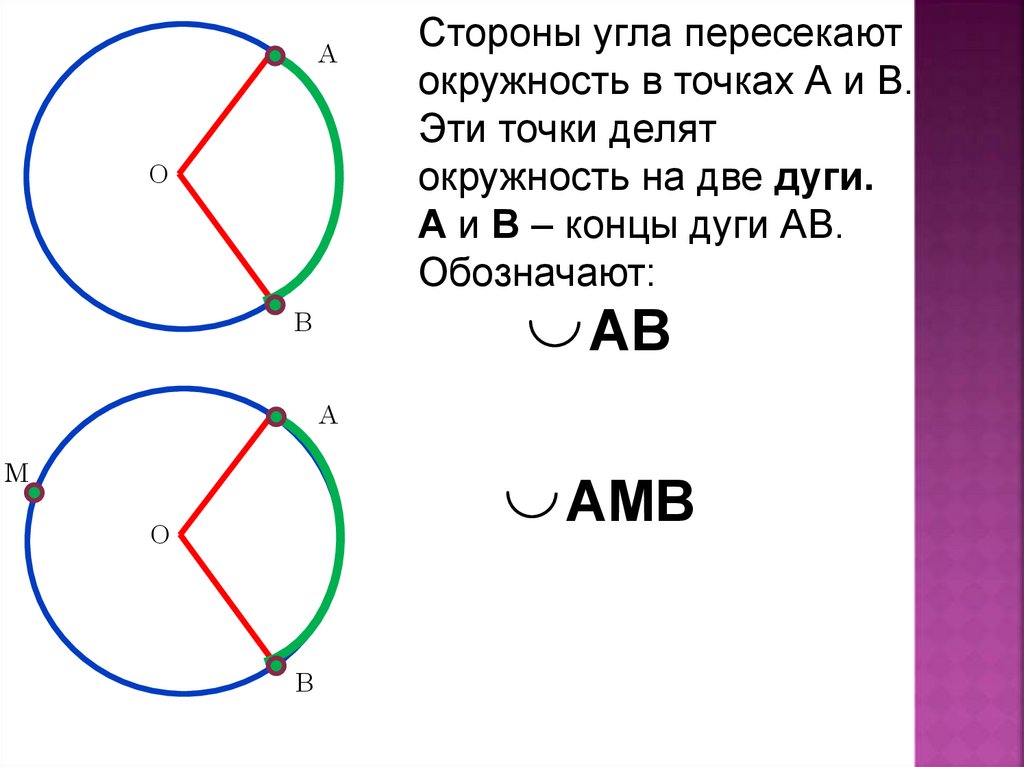
Стороны угла пересекают
окружность в точках А и В.
Эти точки делят
окружность на две дуги.
А и В – концы дуги АВ.
Обозначают:
АВ
В
А
М
АМВ
О
В

4.

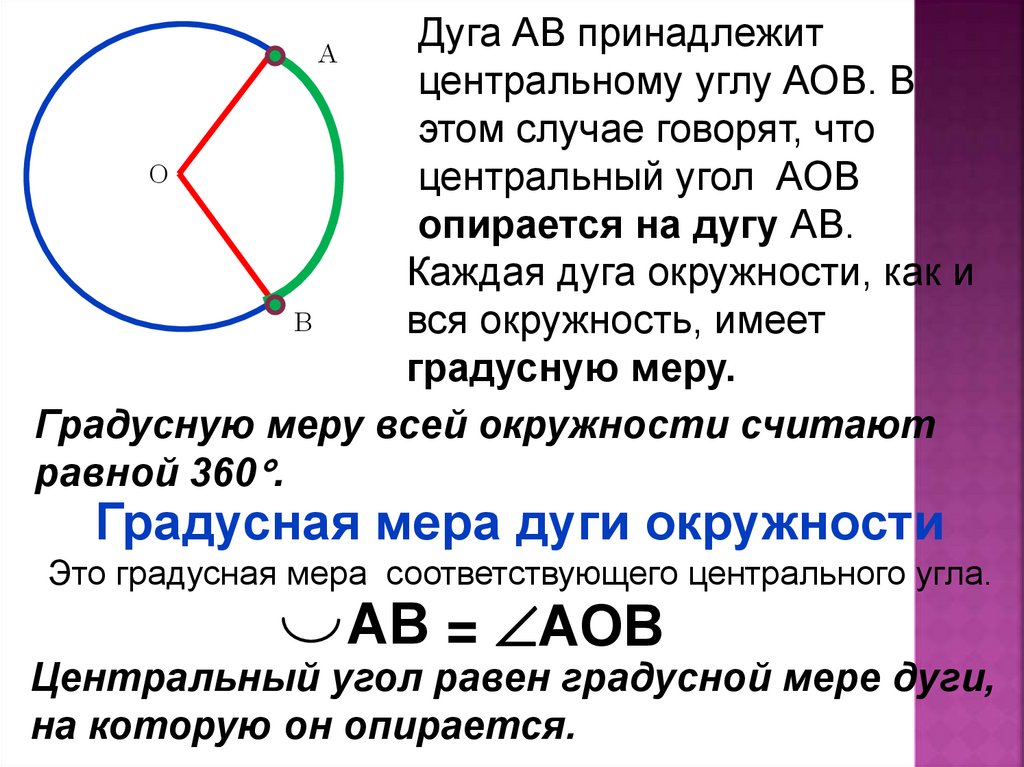
Дуга АВ принадлежит
центральному углу АОВ. В
этом случае говорят, что
О
центральный угол АОВ
опирается на дугу АВ.
Каждая дуга окружности, как и
В
вся окружность, имеет
градусную меру.
Градусную меру всей окружности считают
равной 360 .
А
Градусная мера дуги окружности
Это градусная мера соответствующего центрального угла.
АВ = АОВ
Центральный угол равен градусной мере дуги,
на которую он опирается.

5.

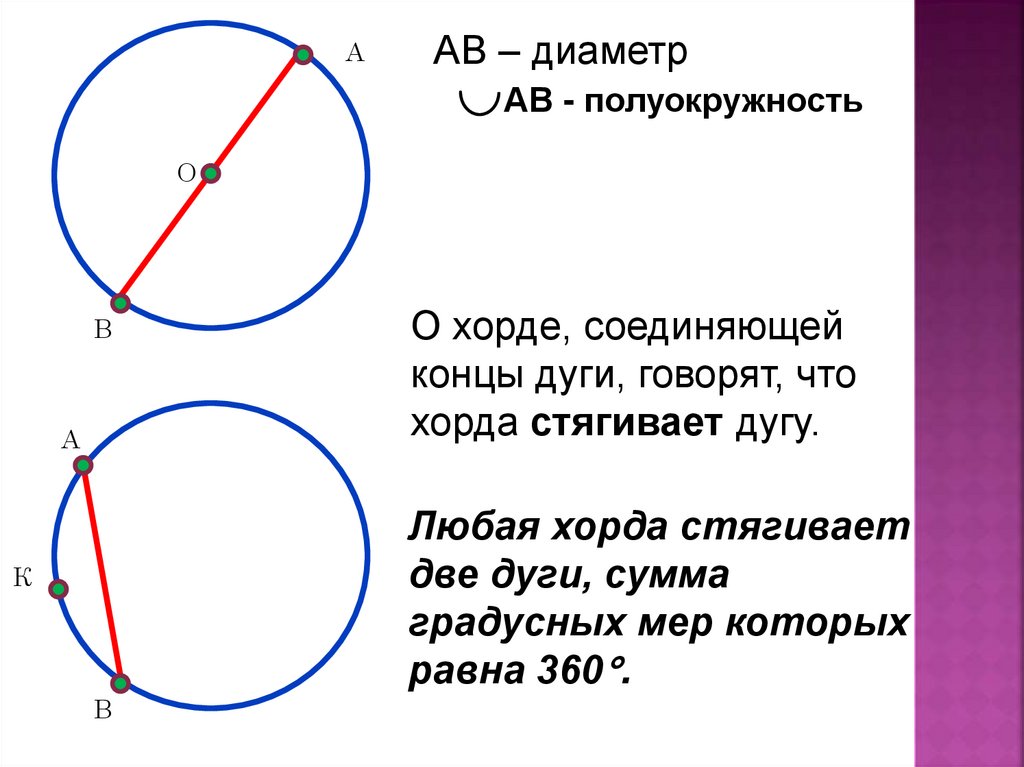
А
АВ – диаметр
АВ - полуокружность
О
В
А
О хорде, соединяющей
концы дуги, говорят, что
хорда стягивает дугу.
Любая хорда стягивает
две дуги, сумма
градусных мер которых
равна 360 .
К
В

6.

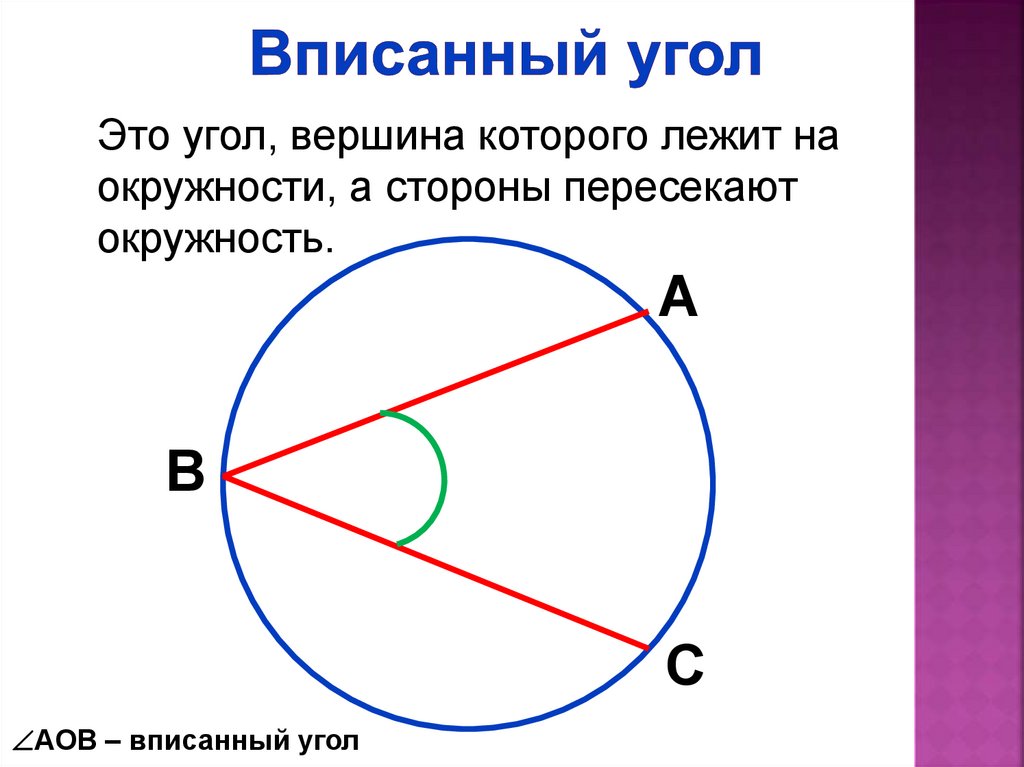
Это угол, вершина которого лежит на
окружности, а стороны пересекают
окружность.
А
В
С
АОВ – вписанный угол

7.

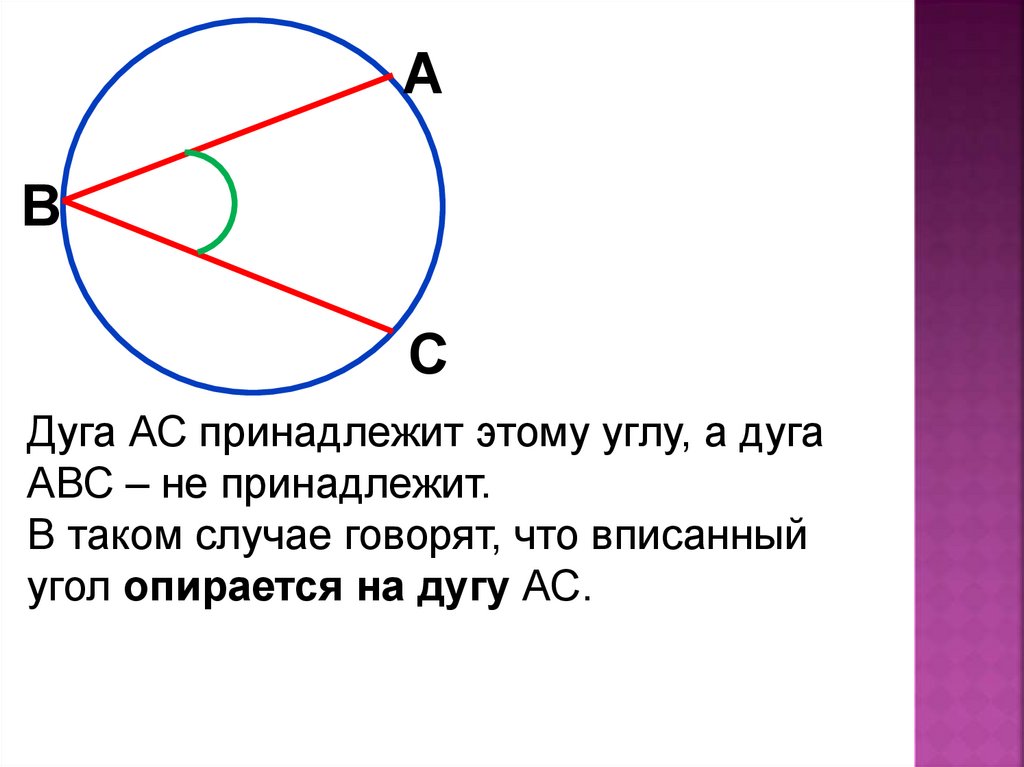
А
В
С
Дуга АС принадлежит этому углу, а дуга
АВС – не принадлежит.
В таком случае говорят, что вписанный
угол опирается на дугу АС.

8.

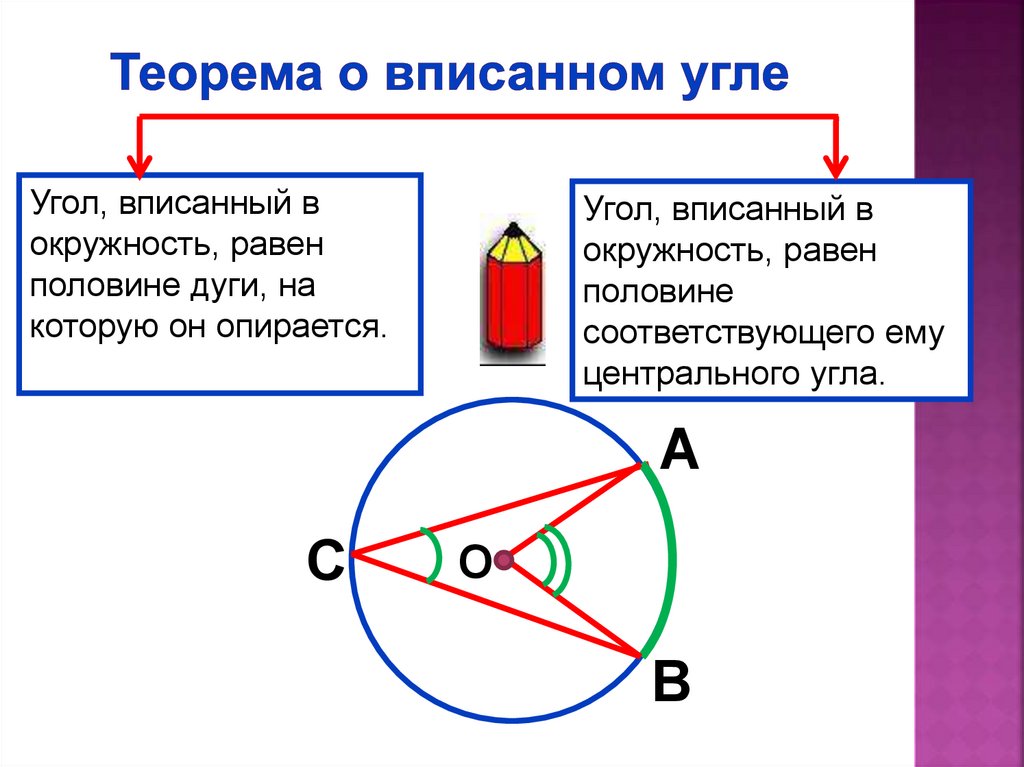
Угол, вписанный в
окружность, равен
половине дуги, на
которую он опирается.
Угол, вписанный в
окружность, равен
половине
соответствующего ему
центрального угла.
А
С
О
В

9.

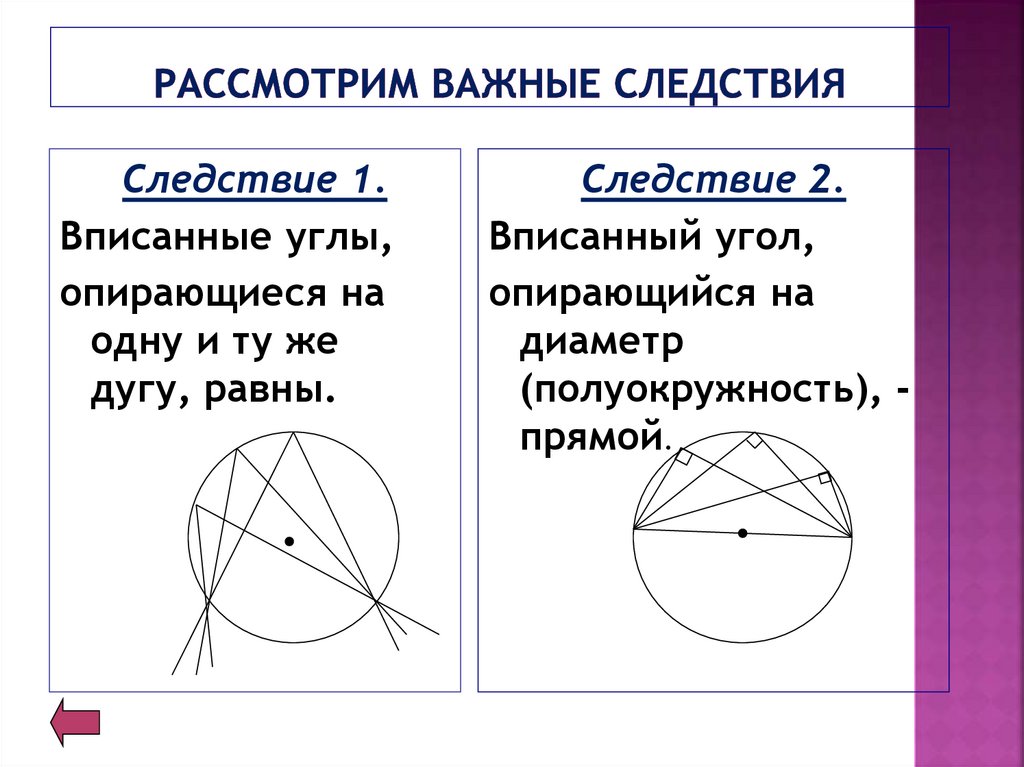
Следствие 1.
Вписанные углы,
опирающиеся на
одну и ту же
дугу, равны.
Следствие 2.
Вписанный угол,
опирающийся на
диаметр
(полуокружность), прямой.

10.

11.

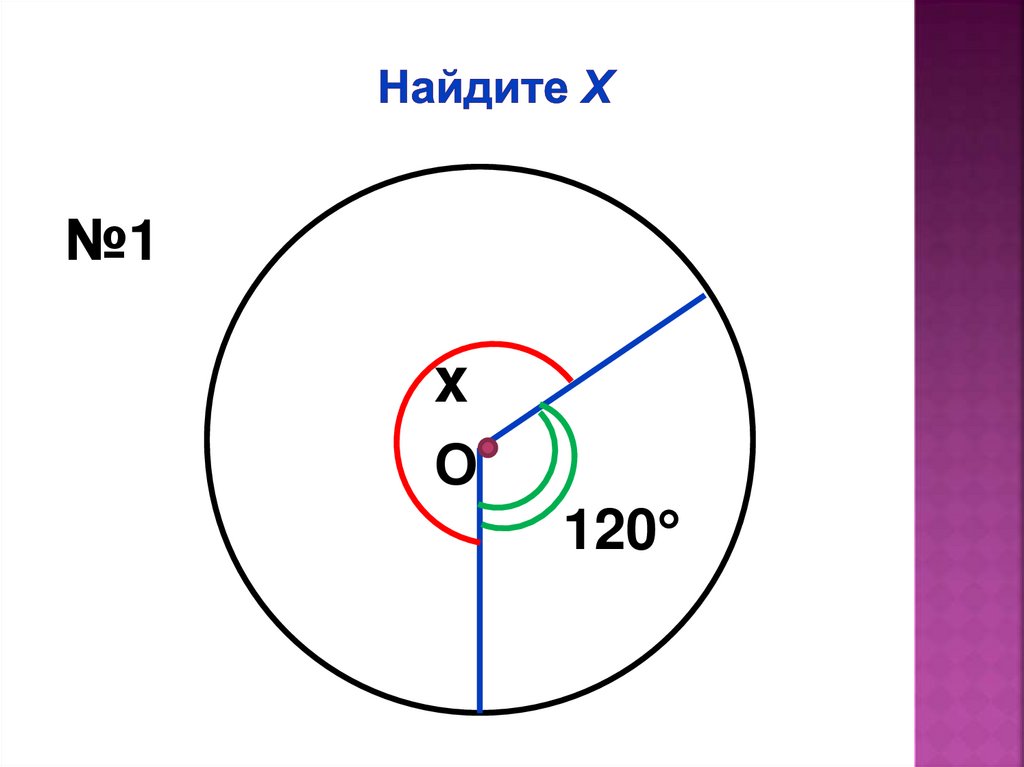
№1
x
О
120

12.

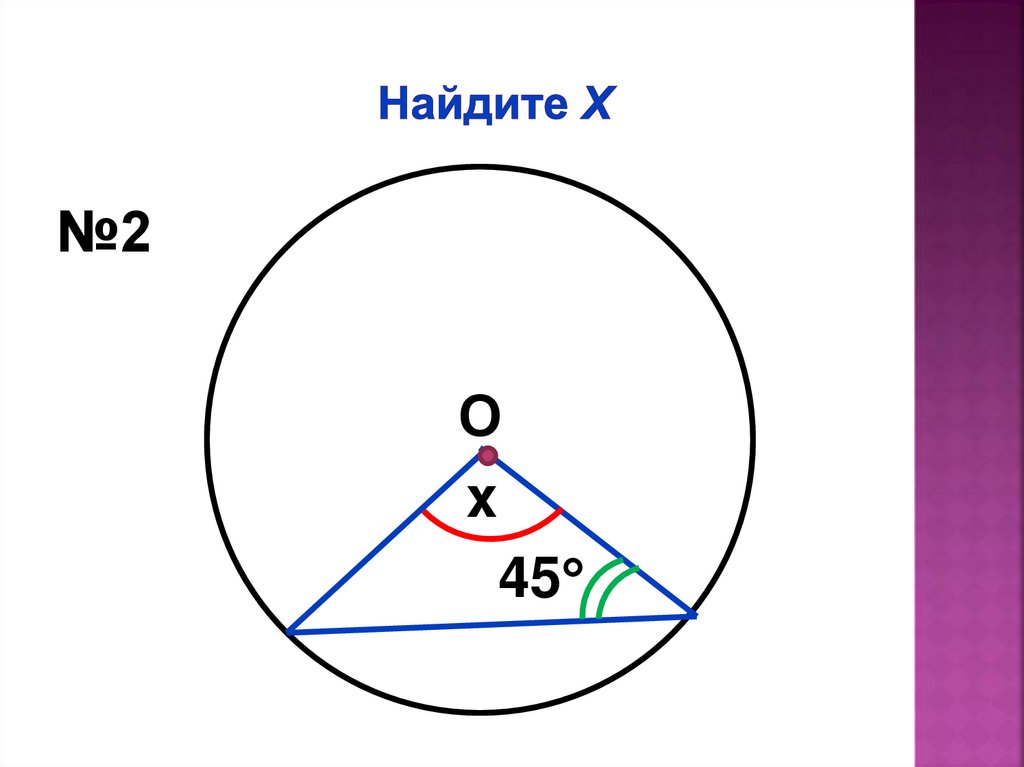
№2
О
x
45

13.

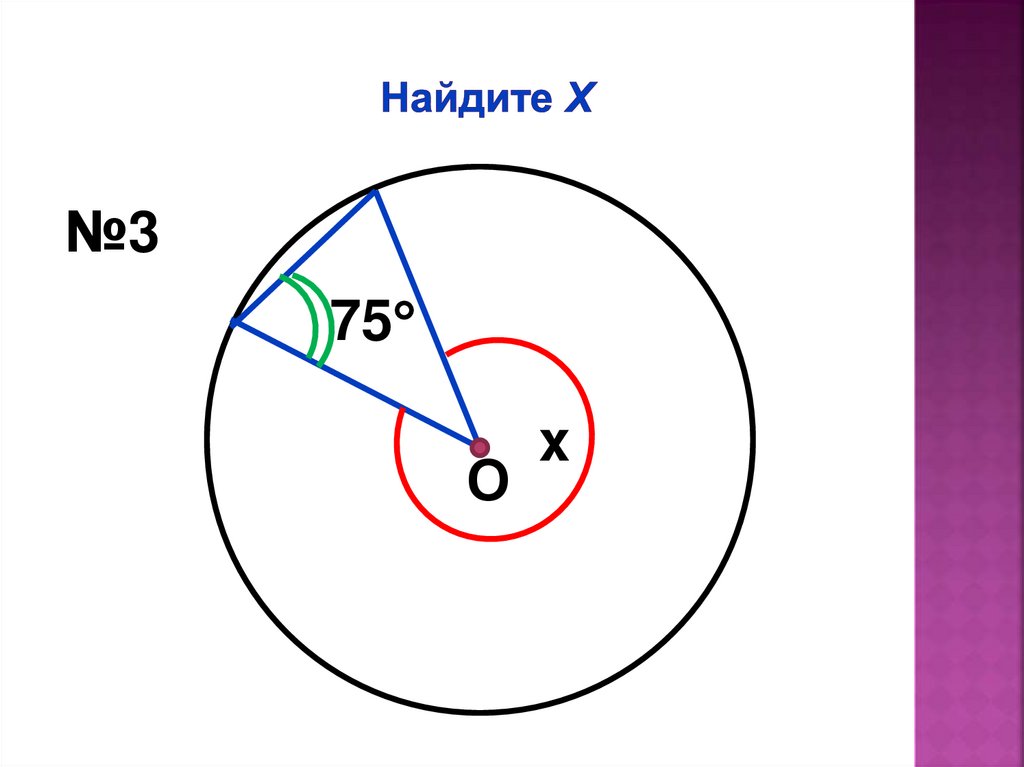
№3
75
О
x

14.

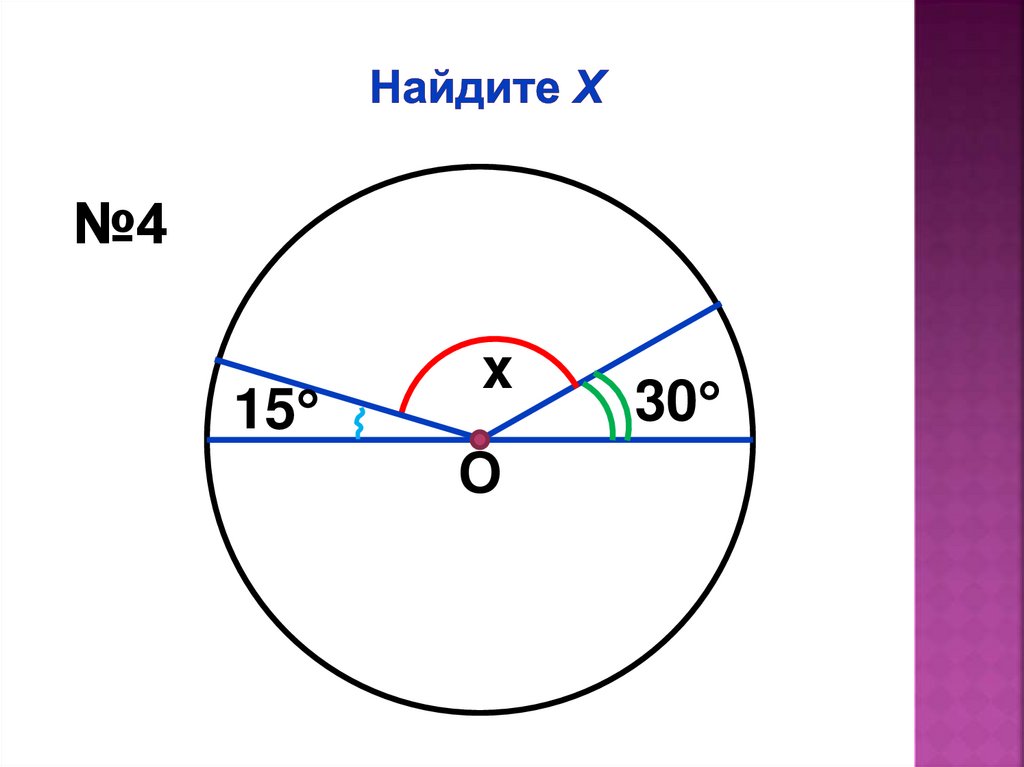
№4
15
x
О
30

15.

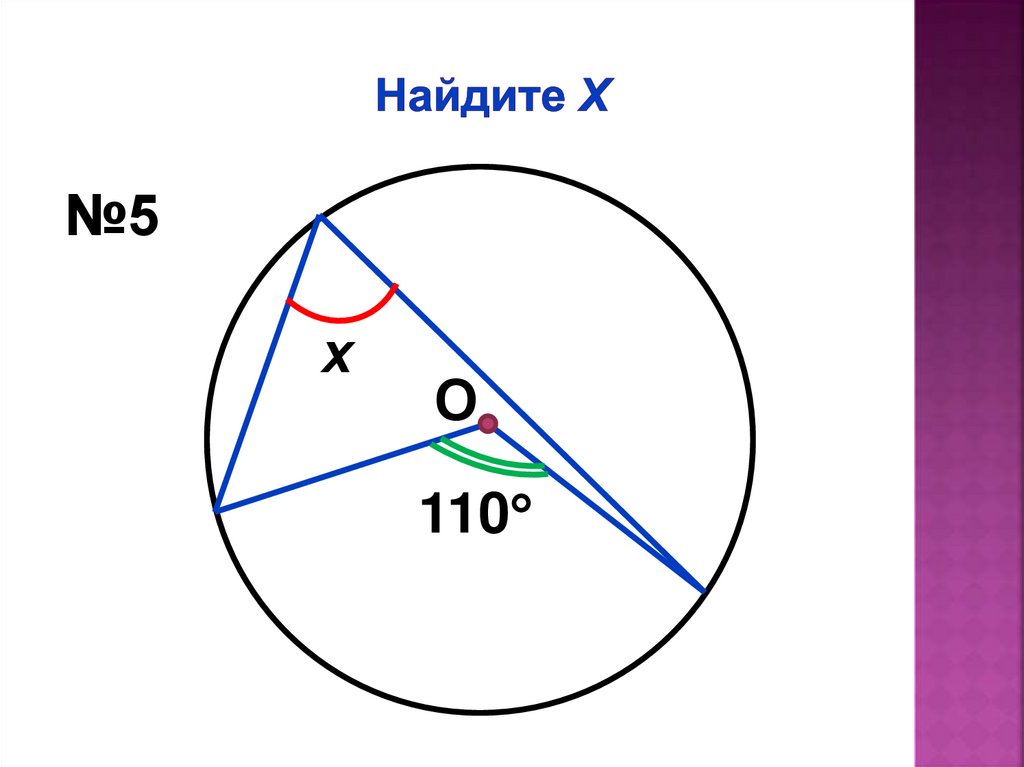
№5
х
О
110

16.

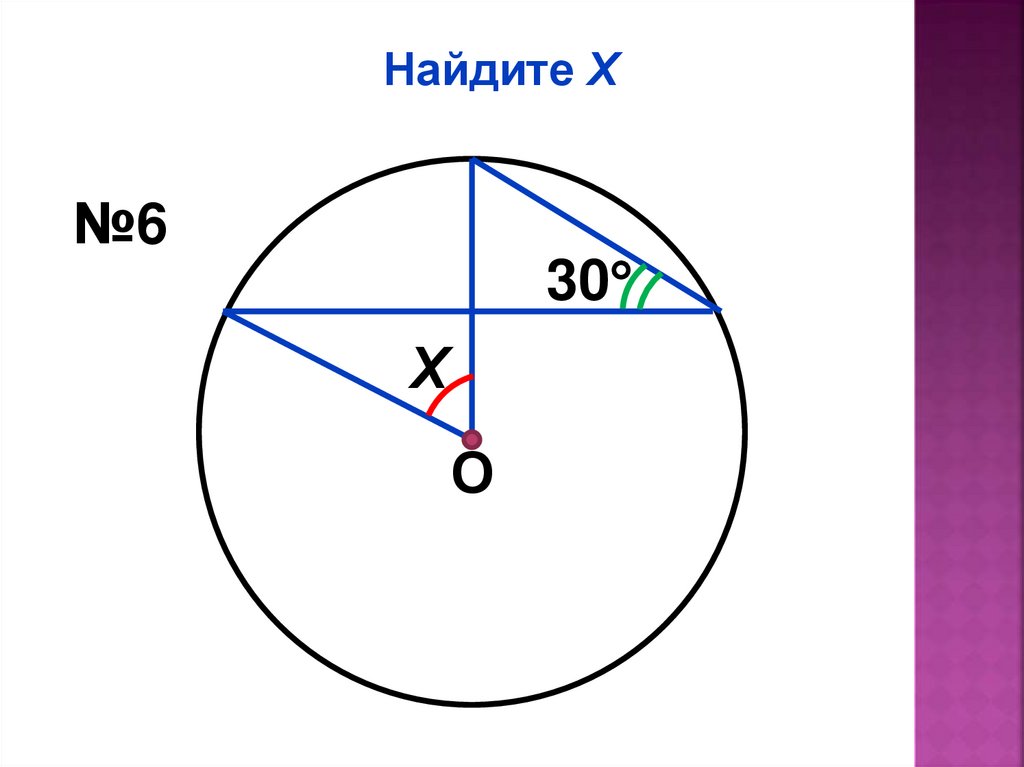
Найдите Х
№6
30
Х
О