Цепи с распределенными параметрами

1.

ЦЕПИ С РАСПРЕДЕЛЕННЫМИ
ПАРАМЕТРАМИ
Лекция ТОЭ2

2.

• До этого мы рассматривали электрические цепи в
которых параметры цепи такие как сопротивление,
индуктивность и емкость были сосредоточены на
отдельных участках. Такие цепи называются цепями
со сосредоточенными параметрами. Но в
некоторых случаях необходимо рассматривать
распределение этих параметров вдоль всей линии,
а не на отдельных участках. Если линия длинная, то
такая необходимость возникает.
• Длинная линия это линия длина которой
соизмеримо с длиной волны передаваемой вдоль
линии сигнала. Длинная линия это понятие
относительное.
• Длина волны определяется отношением фазовой
скорости к частоте.

3.

Ф
f
• λ – длина волны, Ф - фазовая скорость
( 3 108 м/с – близка к скорости света), f- частота,
Гц.
При частоте 50 Гц, длина линии составит:
3 108
6 106 6000км
50
Отсюда можно сказать, что для такой частоты
длинные линии имеют протяженность десятки,
сотни километров

4.

• Если параметры цепи (сопротивление,
индуктивность, емкость и проводимость)
распределены вдоль всей линии, то такие цепи
называются цепями с распределенными
параметрами. Если эти параметры распределены
равномерно, то такие линии называются
однородными. В цепях с распределенными
параметрами ток и напряжение непрерывно
меняются при переходе от одной точки к другой.
Если в цепях со сосредоточенными параметрами
ток и напряжение являлись функциями только
одной переменной времени, то в цепях с
распределенными параметрами ток и напряжение
являются функциями двух независимых
переменных – времени t и координаты х
отсчитываемый вдоль направления распределения
параметров.

5.

• Примерами цепей с распределенными
параметрами являются линии
электропередач, высокочастотные
коаксиальные линии, обмотки
трансформатора и электрических машин.

6.

7.

Схема замещения линии
электропередач с распределенными
параметрами
• Схему замещения линии электропередач с
распределенными параметрами можно
представить в виде совокупности
бесконечно малых участков длиной dx, где х
расстояние от начала линии.

8.

• Первичные параметры линии это
R0, L0, - продольные параметры, R0 - активное
сопротивление обусловленное тепловыми
потерями в проводах, L0 – индуктивность цепи,
определяемая магнитным потоком который
сцепляется с контуром тока образуемым
токоведущими проводами.
G0, C0 - поперечные параметры линии, G0 –
поперечная проводимость или проводимость
утечки вызванная за счет изоляции проводов.
C0 – емкость цепи, обусловлена емкостью между
проводами или проводов по отношению к земле.
Индекс 0 – указывает на то, что параметры приходятся
на единицу длины, то есть погонный параметр.

9.

• Линии с распределенными параметрами являются
однородными, если продольные и поперечные
параметры всех участков равны.
• Вторичными или характеристическими
параметрами линии являются: волновое
сопротивление, коэффициент распространения,
коэффициент затухания, коэффициент фазы.
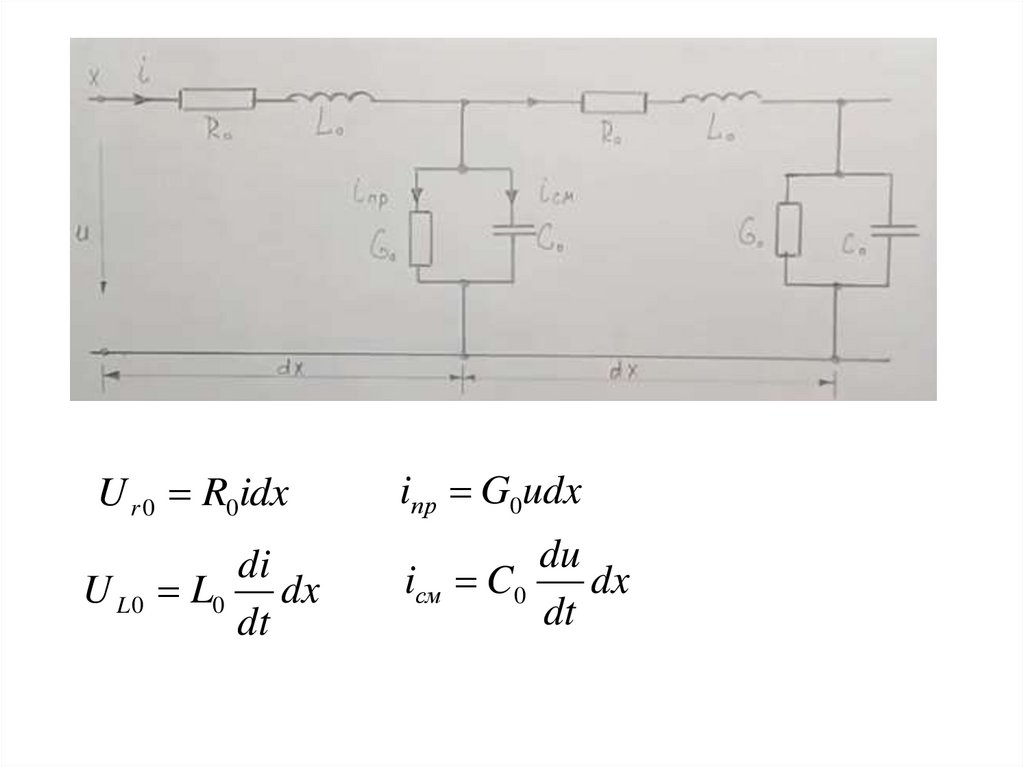
• Отчет координаты х идет от начала линии. Величина
токов в проводах линии зависит не только от
времени, но и от координаты. Поскольку на
каждом участке dx ток ответвляется от одного
провода к другому в виде тока смещения iсм и тока
проводимости iпр .

10.

U r 0 R0idx
iпр G0udx
di
U L 0 L0 dx
dt
du
iсм C0
dx
dt

11.

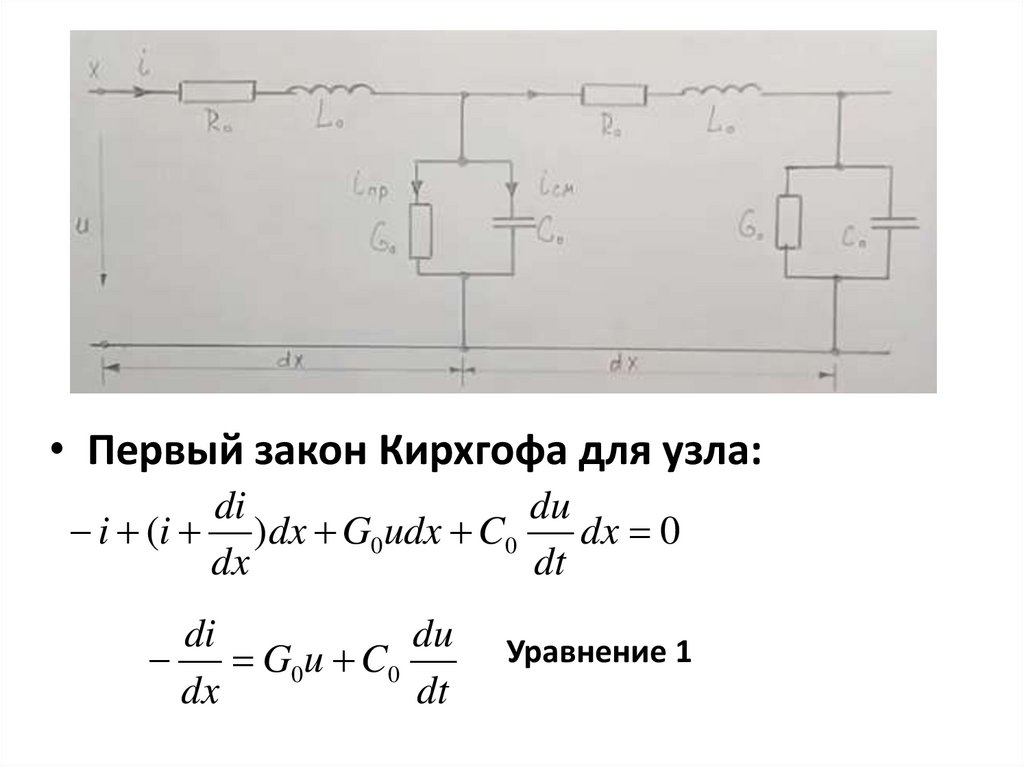
• Первый закон Кирхгофа для узла:
di
du
i (i )dx G0udx C0
dx 0
dx
dt
di
du
G0u C0
dx
dt
Уравнение 1

12.

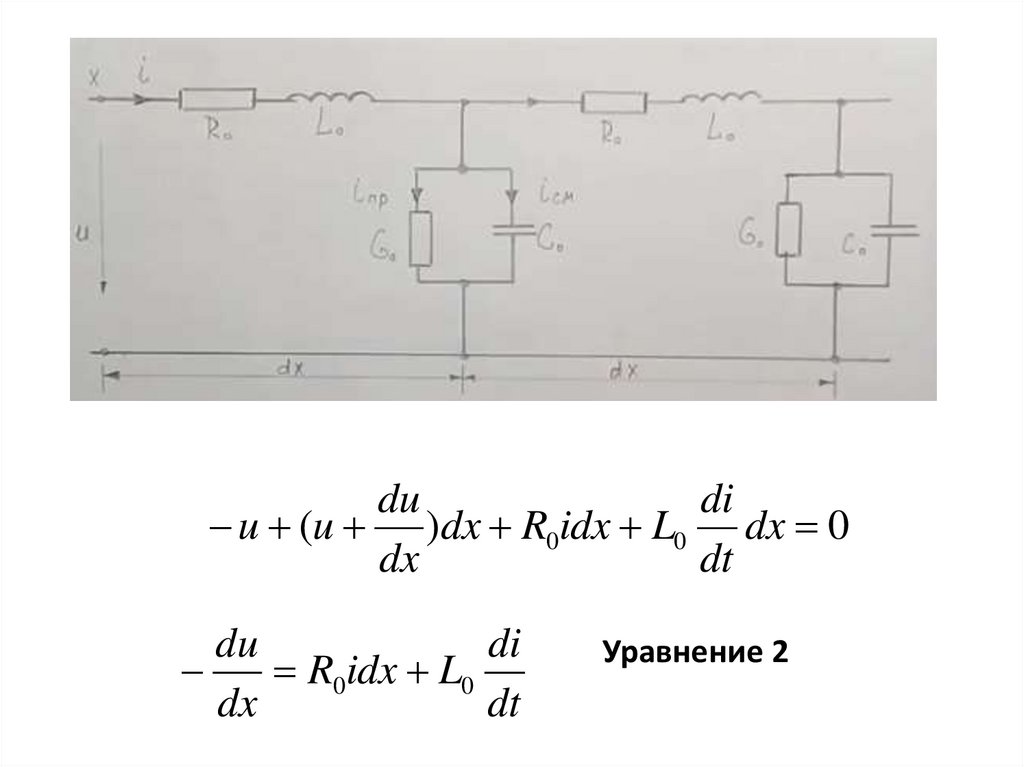
du
di
u (u )dx R0idx L0 dx 0
dx
dt
du
di
R0idx L0
dx
dt
Уравнение 2

13.

• Уравнения 1 и 2 называются телеграфными
уравнениями.
• Рассмотрим как решаются уравнения
однородной линии при установившемся
синусоидальном режиме. В этом случае
перейдем комплексам напряжения и тока
которые не зависят от времени.
Следовательно, в частных производных
сводятся к обычным дифференциальным
уравнениям:

14.

du
di
R0idx L0
dx
dt
dU
R0 I j L0 I (1)
dx
di
du
G0u C0
dx
dt
dI
G0U j C0 U (2)
dx
Продифференцируем первое уравнение
d 2U
dI
dI
2 R0
j L0
dx
dx
dx
Подставим в получившийся выражение dI/dx
из 2 уравнения:

15.

d 2U
2 R0 (G0U j C0 U ) j L0 (G0U j C0 U )
dx
( R0 j L0 )(G0U j C0 U )
( R j L )(G j C )U Y 2U
0
0
0
0
Y ( R0 j L0 )(G0 j C0 )
Y j
Y – называется коэффициентом распространения,
α – коэффициент затухания
β – коэффициент фазы