Основы радиотехнических методов получения и передачи информации Занятие № 3. Методы спектрального анализа сигналов и помех

1.

Федеральное государственное бюджетное образовательное учреждение
высшего образования
«МИРЭА – Российский технологический университет»
РТУ МИРЭА
ВОЕННЫЙ УЧЕБНЫЙ ЦЕНТР
КАФЕДРА ВОЗДУШНО-КОСМИЧЕСКИХ СИЛ
Дисциплина «Военно-специальная подготовка 01»
«Основы авиационной техники»
(ВУС – 141100, 541100)
Тема № 1. Основы радиотехнических методов
получения и передачи информации
Занятие № 3. Методы спектрального анализа
сигналов и помех
ВУЦ РТУ МИРЭА
27 февраля 2025 г.

2.

2
Контрольный опрос (5мин.):
Вариант 1
1. Детерминированные сигналы – это……
Вариант 2
1. Случайные сигналы – это……….

3.

3
Лекция 1.3 «Метод спектрального
анализа сигналов и помех»
Вопросы:
1. Спектральный анализ детерминированных
периодических сигналов.
2. Спектральный анализ детерминированных
непериодических сигналов.

4.

Спектральный анализ детерминированных
периодических сигналов
4
Вопрос 1.
Наиболее наглядным способом описания исследуемого сигнала s(t)
является его представление в виде системы взаимосвязанных функций
времени: 0 (t ), 1 (t ), 2 (t ),..., i (t ),... - называемой базисной. (1)
Представление сигнала s(t) значительно упрощается если выбранная
система базисных функций i (t ) обладает свойством ортогональности
и нормированности (т.е. ортонормированности).
Если для любой пары функций из ортогональной системы (1)
выполняется условие: t2
1, i k
i (t ) k (t )dt
,
(2)
t1
0,
i k
то такая система функций – ортонормированна.
Прим.
Ортонорми́рованная система — ортогональная система, у которой каждый
элемент системы имеет единичную норму.

5.

Спектральный анализ детерминированных
периодических сигналов
5
Если на временном интервале [t1, t2] действует произвольный сигнал s(t)
и выбрана ортонормированная система функций (1), то этот сигнал может быть
представлен о б о б щ е н н ы м р я д о м Ф у р ь е :
s (t ) ci i (t ) ,
(3)
i 0
где: ci - некоторые постоянные коэффициенты.
После выполнения соответствующих выкладок можно доказать,
что постоянный коэффициент
c i с номером i k будет рассчитываться
по формуле:
t2
ck s(t ) k (t )dt .
(4)
t1
Совокупность коэффициентов ck полностью определяет сигнал s(t)
и называется с п е к т р о м .
Из теории известно, что при выбранной ортонормированной системе
функций k (t ) и фиксированном числе слагаемых ряда (3) наилучшим образом
аппроксимировать сигнал s(t) позволяет о б о б щ е н н ы й р я д Ф у р ь е
(в этом состоит его главное свойство).
Представление детерминированных сигналов в виде постоянной
составляющей и суммы гармонических колебаний с кратными частотами
называется спектральным разложением.

6.

Спектральный анализ детерминированных
периодических сигналов
6
1.1. Периодические импульсные сигналы
При спектральном представлении периодических сигналов наиболее
удобен ортонормированный базис гармонических функций вида:
1
,
T
2
cos 1t ,
T
2
sin 1t ,....,
T
2
cos n 1t ,
T
2
sin n 1t (5)
T
1 2 T - частота следования импульсов периодического сигнала
Ортонормированный базис гармонических функций удобнее всего
рассматривать
на интервале: [ T 2, T 2]
]
Спектральное разложение периодического сигнала может быть
представлено тригонометрической формой ряда Фурье:
a 0
s (t ) a n cos n 1t bn sin n 1t
(6)
2 n 1
T 2
Прим.
2
s(t )dt (7)
В соотношении (6): a0
Ряд Фурье — это тригонометрический ряд,
T T 2
где в качестве простейших используются
функции синуса и косинуса.
- постоянная составляющая:
T 2
2
an
s (t ) cos n 1tdt
T T 2
(8)

7.

Спектральный анализ детерминированных
периодических сигналов
7
T 2
2
- амплитуды косинусоидальных составляющих: bn
s(t ) sin n 1tdt (9)
T T 2
- амплитуды синусоидальных составляющих сигнала.
Составляющую с частотой 1 принято называть первой (основной) гармоникой.
Составляющие с частотами n 1 ( n 1)
– принято называть высшими
гармониками периодического сигнала.
Из математики известно, что если сигнал представляет собой
четную функцию времени
, то в тригонометрической форме записи
ряда Фурье (6) остаются только косину
соидальные составляющие a n а амплитуды
синусоидальных bn
составляющих
обращаются в ноль.
Для сигнала s(t), представляющего собой нечетную функцию, наоборот,
в ноль обращаются амплитуды a n и ряд состоит только из синусоидальных
составляющих с амплитудами bn .

8.

Спектральный анализ детерминированных
периодических сигналов
8
s(t ) A0 An cos( n 1t n ) (10)
n 1
где: A0 a0 2
An an2 bn2 -амплитуда, n arctg (bn / an ) -начальная фаза n-ной
гармоники сигнала
В теории сигналов также широко используется комплексная форма
ряда Фурье:
s (t )
C n e jn 1t (11)
n 1
T 2
1
jn 1t
s
(
t
)
e
dt - комплексная амплитуда n-ой гармоники (12)
где: Cn
T T 2
Наглядное представление о спектре сигнала дает его графическое
изображение – спектральная диаграмма. Различают амплитудно-частотные
и фазо-частотные спектры.

9.

Спектральный анализ детерминированных
периодических сигналов
9
Распределение амплитуд гармоник
по частоте называют
An
амплитудно-частотным спектром (АЧС) или амплитудным спектром.
Распределение начальных фаз n гармоник по частоте называют
фазо-частотным спектром (ФЧС) или спектром фаз. Распределение
комплексных амплитуд C n гармоник называется комплексным спектром.
На спектральных диаграммах по оси абсцисс откладывают частоту,
а по оси ординат – амплитуду или фазу соответствующих составляющих.
Спектр периодического сигнала называют линейчатым (дискретным),
т.к. он состоит из отдельных линий, соответствующих гармоническим
составляющим сигнала.

10.

Спектральный анализ детерминированных
периодических сигналов
10
1.2. Биполярные прямоугольные видеоимпульсы (меандр)
Рис. 1. Временная диаграмма биполярных
прямоугольных импульсов (меандра)
Меандр является нечетной функцией, поэтому амплитуды косинусоидальных
составляющих этого сигнала будут равны нулю, амплитуды синусоидальных
составляющих bn будут рассчитываться по формуле:
T 2
T
2
T
2
4E
4E
cos n 1t 02
bn
s(t ) sin n 1tdt
sin n 1tdt
T T 2
T 0
nT 1
(13)

11.

Спектральный анализ детерминированных
периодических сигналов
Учитывая, что 1 2 T Упростим выражение (13) и получим: bn
11
2E
1 cos(n ) (14)
n
Таким образом, амплитуды синусоидальных составляющих с четными
номерами (т.е., когда n = 2,4... будут равняться нулю ( bn = 0 ), а амплитуты
синусоидальных составляющих с нечетными номерами (n = 1,3..) будут
определяться по формуле: b 4 E , в результате меандр можно записать в
n
n
виде:
4E
1
1
s t
sin 1t sin 3 1t sin 5 1t
(15)
3
5
Рис. 2. Амплитудно-частотный
и фазо-частотный спектр меандра

12.

Спектральный анализ детерминированных
периодических сигналов
12
1.3. Последовательность униполярных прямоугольных
видеоимпульсов
Рис. 3. Временная диаграмма последовательности
униполярных прямоугольных видеоимпульсов
Функция, описывающая периодическую последовательность однополярных
прямоугольных видеоимпульсов - четная (рис. 3). Для такого сигнала амплитуды
синусоидальных составляющих будут равны нулю (bn = 0), а амплитуды
косинусоидальных составляющих будут определяться как:
и
2
an
T
и
n и
4E 2
2E
2 n
s
t
cos
n
tdt
cos
t
dt
sin
1
0 T
T
n
T
и
2
2

13.

Спектральный анализ детерминированных
периодических сигналов
с учетом того, что скважность сигнала q
постоянная составляющая:
и
и
a0
1
2
T
сам сигнал запишем в виде:
s t
T
иE
T
n
sin 1 и
2E
2
an
n 1 и
q
2
2
s t dt
и
иE
13
(16)
(17)
T
2
1
n и
sin
cos n 1t (18)
n 1 n
T
2E
При этом количество спектральных составляющих в одном лепестке
определяется как:
n 2q 1
Фазы гармоник определим из соотношения n arctg bn an . Учитывая, что
bn 0 , получим n arctg
0
m , где m 0,1,2,...
an

14.

Спектральный анализ детерминированных
периодических сигналов
14
В формуле (16) второй множитель – имеет вид функции «арочный синус».
Из математики известны свойства функции sin( x) x :
- при x 0
sin( x)
1;
x
- функция обращается в ноль в точках x , 2 ,... и затухает с ростом
аргумента x .
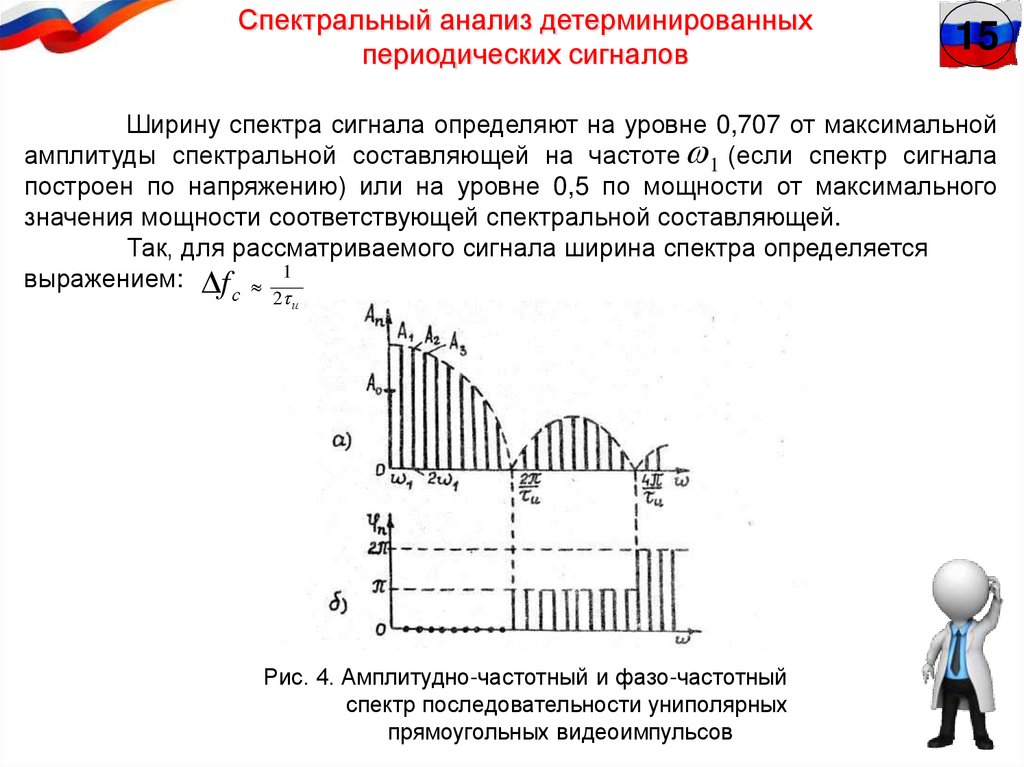
Анализ полученного спектра амплитуд (рис. 4, a) позволяет заключить:
- АЧС представляет бесконечный дискретный набор гармоник,
sin x
n
амплитуды которых модулированы по закону функции
, где: x 1 и ;
2
x
- интервал между гармониками по оси частот равен частоте повторения
импульсов 1 ;
- найденный АЧС в значительной степени зависит от соотношения
периода повторения T и длительности импульса и, так при и const
с увеличением периода повторения T основная частота 1 2 T уменьшается
и спектр становится плотнее;
- число гармоник в каждом «лепестке» АЧС определяется скважностью q
сигнала;
- при T const , с уменьшением длительности импульса ( и), ширина
спектра увеличивается.

15.

Спектральный анализ детерминированных
периодических сигналов
15
Ширину спектра сигнала определяют на уровне 0,707 от максимальной
амплитуды спектральной составляющей на частоте 1 (если спектр сигнала
построен по напряжению) или на уровне 0,5 по мощности от максимального
значения мощности соответствующей спектральной составляющей.
Так, для рассматриваемого сигнала ширина спектра определяется
выражением: f 1
с
2 и
Рис. 4. Амплитудно-частотный и фазо-частотный
спектр последовательности униполярных
прямоугольных видеоимпульсов

16.

Спектральный анализ детерминированных
непериодических сигналов
16
Вопрос 2.
Период следования: T .
Пусть s(t)=u(t) - одиночный импульсный сигнал конечной длительности
(рис. 7, а). Мысленно дополнив его такими же сигналами, следующими
с некоторым интервалом T (рис. 7, б), получим периодическую
последовательность аналогичных импульсов.
Увеличим в пределе T и все импульсы уйдут вправо и влево
в бесконечность, апериодическая последовательность станет одиночным
импульсом.
Рис. 5. Временная диаграмма
одиночного импульса (а)
и его периодического продолжения (б)

17.

Спектральный анализ детерминированных
непериодических сигналов
17
Сигнал описывается с помощью прямого и обратного преобразования Фурье::
S ( ) s(t )e j t dt
(20)
1
j t
s (t )
S
(
)
e
d
2
(21)
Эти преобразования связывают между собой вещественную функцию
времени s(t) и комплексную функцию частоты S ( ).
Функцию S ( ) называют спектральной плотностью, она характеризует
интенсивность
сплошного
распределения
амплитуд
гармоник
непериодического сигнала вдоль оси частот. В этом состоит основное отличие
спектральной плотности непериодического сигнала от дискретного спектра
периодического сигнала.
Прим.
Преобразование Фурье – это математический метод, применяемый для
анализа сигналов. Он даёт возможность преобразовать данные
из временной области в частотную, разлагая их на составляющие.

18.

Спектральный анализ детерминированных
непериодических сигналов
18
и
и
U
;
при
t
2
2
Одиночный прямоугольный видеоимпульс: U (t )
0; при t и и t и
и
2
2
2
j
t
Тогда: S ( ) Ue
dt
Пример:
и
2
После проведения прямого преобразования Фурье прямоугольного
видеоимпульса получим выражение, описывающее спектральную плотность
данного сигнала, которая будет иметь вид:ть вид:
U(t)
U
S ( ) 2U и
sin(
и
2
)
и
2
Прим.
и/2
и/2
t Одиночный прямоугольный видеоимпульс — это
0
непериодический сигнал, основным параметром
Рис. 6. Временная диаграмма которого является длительность τ.
одиночного прямоугольного
видеоимпульса

19.

Спектральный анализ детерминированных
непериодических сигналов
19
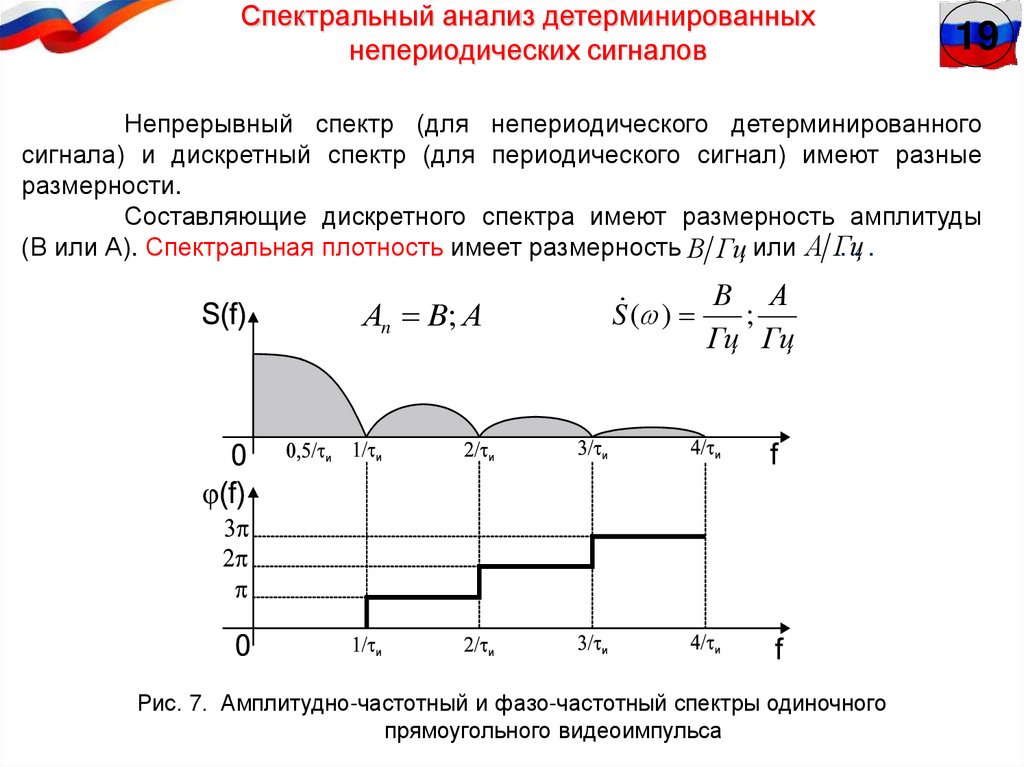
Непрерывный спектр (для непериодического детерминированного
сигнала) и дискретный спектр (для периодического сигнал) имеют разные
размерности.
Составляющие дискретного спектра имеют размерность амплитуды
(В или А). Спектральная плотность имеет размерность В Гц или А Гц
...
Аn B; А
В А
S ( )
;
Гц Гц
Рис. 7. Амплитудно-частотный и фазо-частотный спектры одиночного
прямоугольного видеоимпульса

20. Задание на самостоятельную работу:

20
Задание на самостоятельную
работу:
Изучить теоретический материал, используя следующую
литературу:
1. Радиоэлектронные средства систем управления ПВО и ВВС/ Под ред.
В.Д. Казакова. - М.:Воениздат,1987, стр. 21 - 25.
2. Основы теории РЭБ/ Под ред. Н. Ф. Николенко. - М.:Воениздат,1987,
стр. 31 - 74.
3. Ю.С. Филимонов, С.В. Филатов. Основы радиоэлектроники, часть 1. М.:МИРЭА,1996., стр. 29 - 40.
4. Основы построения объектов подавления авиационными средствами
радиоэлектронной борьбы: Учебное пособие. / Ф.Г. Машошин, А.Г. Мусихин,
Д.Н. Корабейников, В.С. Мартьянов. Московский технологический
университет (МИРЭА) – М. 2016, стр. 12 - 18.