Similar presentations:
Структурные средние величины
1.
Кафедра ЭКОНОМИКИСТРУКТУРНЫЕ
СРЕДНИЕ ВЕЛИЧИНЫ
2. Компетенции:
в подготовительных мероприятиях передрасчётами;
в проведении оценки правильности расчётов
соответствующих величин;
в понимании значения структурных средних и
экономической интерпретации полученных
результатов при расчёте моды и медианы ряда
данных, характеризующих различные процессы и
явления.
3.
4. Мо
• Мода - значение признаканаиболее часто встречающееся
в вариационном ряду.
5. Ме
• Медиана - значениеварьирующего признака,
приходящееся на середину
ряда, варианта, делящая ряд
на две равные части
6.
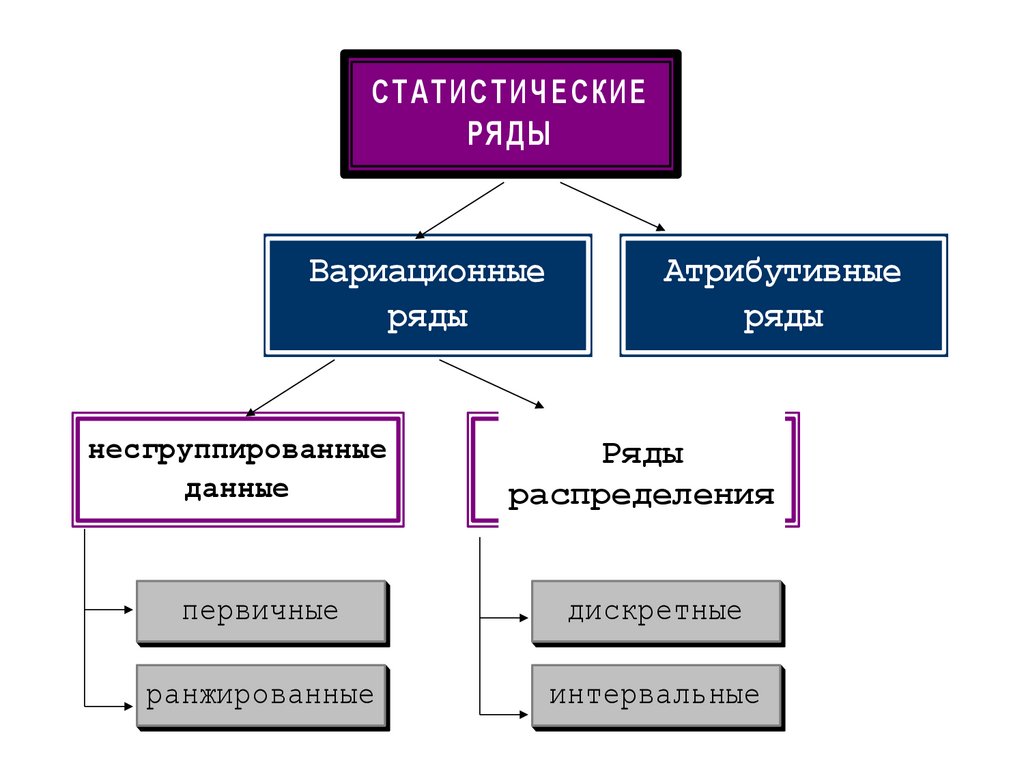
СТ АТ ИСТ ИЧЕСКИЕРЯДЫ
Вариационные
ряды
Атрибутивные
ряды
несгруппированные
данные
сгруппированные
Ряды
данные
распределения
первичные
дискретные
ранжированные
интервальные
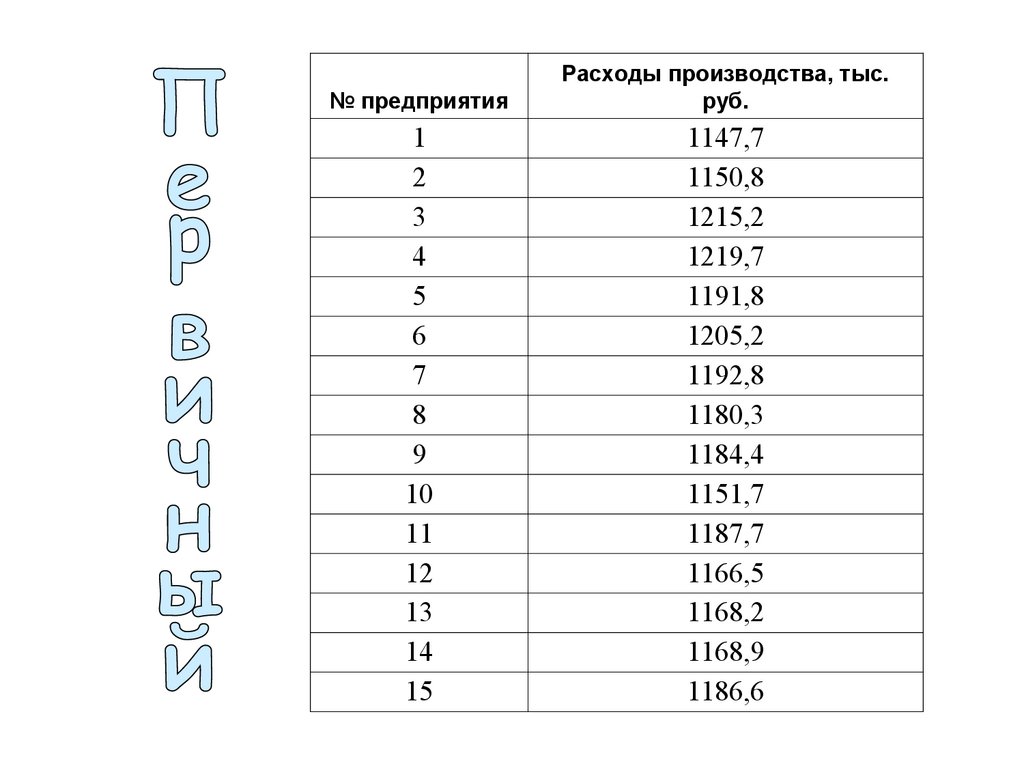
7. ПЕРВИЧНЫЙ РЯД
Моды и медианыпервичного ряда
не существует!
8.
№ предприятияРасходы производства, тыс.
руб.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1147,7
1150,8
1215,2
1219,7
1191,8
1205,2
1192,8
1180,3
1184,4
1151,7
1187,7
1166,5
1168,2
1168,9
1186,6
9. РАНЖИРОВАННЫЙ РЯД
Моды несуществует!
10. РАНЖИРОВАННЫЙ РЯД
Медиана - центральнаяварианта при нечетном
числе единиц
совокупности, при четном
числе она равна полусумме
серединных вариант
11.
№ предприятия1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Расходы
производства,
тыс. руб.
1147,7
1150,8
1151,7
1166
1167,8
1168,2
1168,9
1180
1184,4
1186,6
1187,7
1191
1192,8
1205,2
1215,2
Mе 1180
12.
СТРУКТУРНЫЕ СРЕДНИЕ ДЛЯСГРУППИРОВАННЫХ ДАННЫХ
Определение:
Кумулятивная (накопленная) частота
(Si)- результат суммирования
предшествующей кумулятивной частоты
с частотой текущей группы. Для
первой группы кумулятивная частота
равна частоте в группе.
13.
МОДАдискретного
ряда
МЕДИАНА
дискретного
ряда
определяется
по наибольшей
частоте
признака
определяется
по кумулятивной
частоте
признака
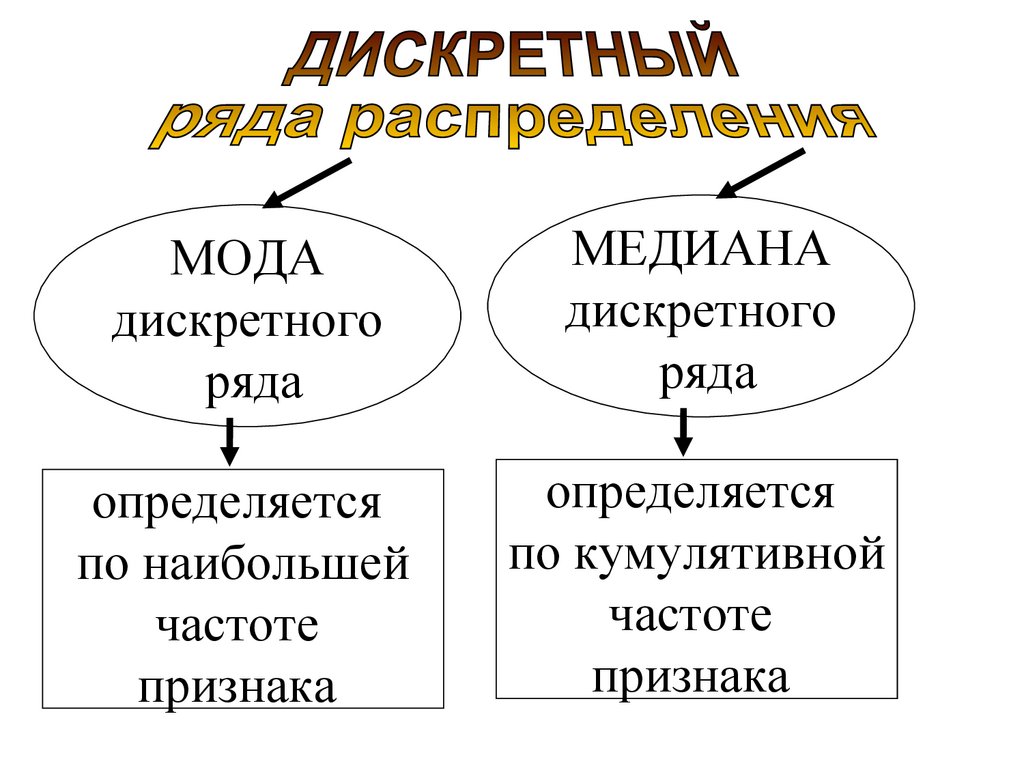
14. ДИСКРЕТНЫЙ РЯД
Мода и медиана - конкретныеварианты
•Мода - варианта с
максимальной частотой,
•Медиана - варианта с
кумулятивной частотой,
превышающей полусумму
f
i
частот S
Ме
2
15.
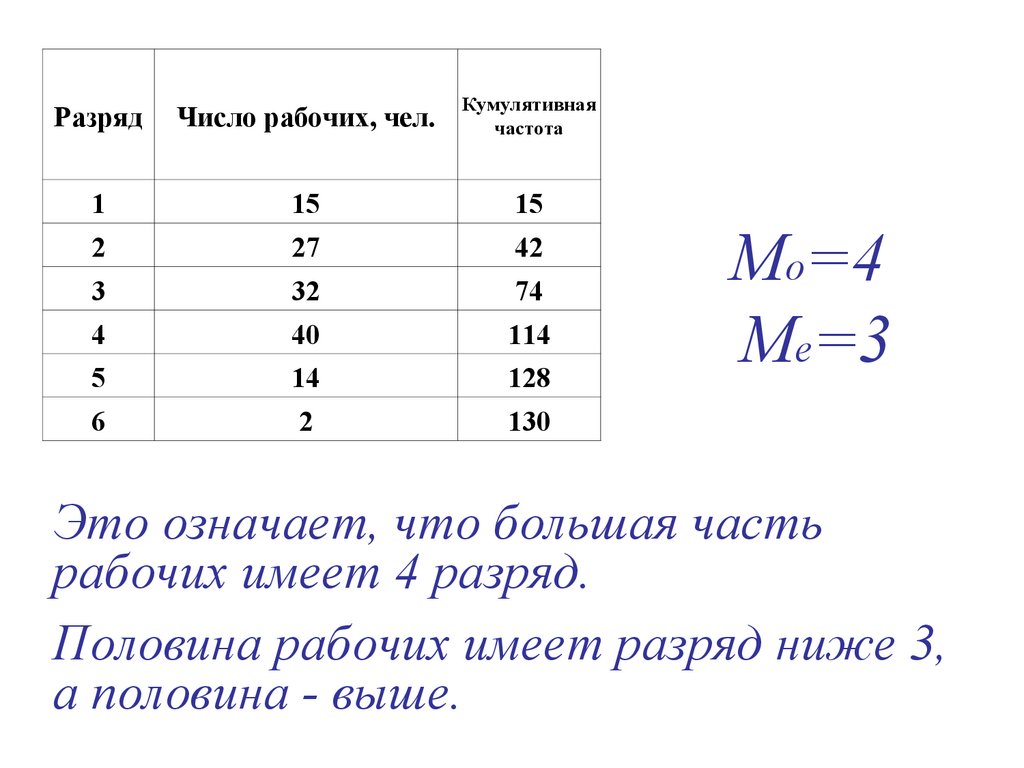
РазрядЧисло рабочих, чел.
1
15
2
27
3
32
4
40
5
14
6
2
Найти моду и медиану
дискретного ряда, сделать
выводы.
16.
РазрядЧисло рабочих, чел.
Кумулятивная
частота
1
15
15
2
27
42
3
32
74
4
40
114
5
14
128
6
2
130
Мо=4
Ме=3
Это означает, что большая часть
рабочих имеет 4 разряд.
Половина рабочих имеет разряд ниже 3,
а половина - выше.
17.
МОДАинтервального
ряда
МЕДИАНА
интервального
ряда
определяется по
специальной
методике
определяется по
специальной
методике
18. ИНТЕРВАЛЬНЫЙ РЯД
•Определение 1•Модальный интервал интервал с максимальной
частотой
•Определение 2
•Медианный интервал интервал, у которого
fчастота
кумулятивная
не
i
S
Ме
менее полусуммы
частот
2
19.
СТРУКТУРНЫЕ СРЕДНИЕ ДЛЯСГРУППИРОВАННЫХ ДАННЫХ
Определение:
Кумулятивная (накопленная) частота
(Si)- результат суммирования
предшествующей кумулятивной частоты
с частотой текущей группы. Для
первой группы кумулятивная частота
равна частоте в группе.
20.
M o xМof M o f M o 1
( f M o f M o 1 ) ( f M o f M o 1 )
hМ o
21.
fiS M e 1
2
M e xМe
hМ e
fMe
22.
23.
24.
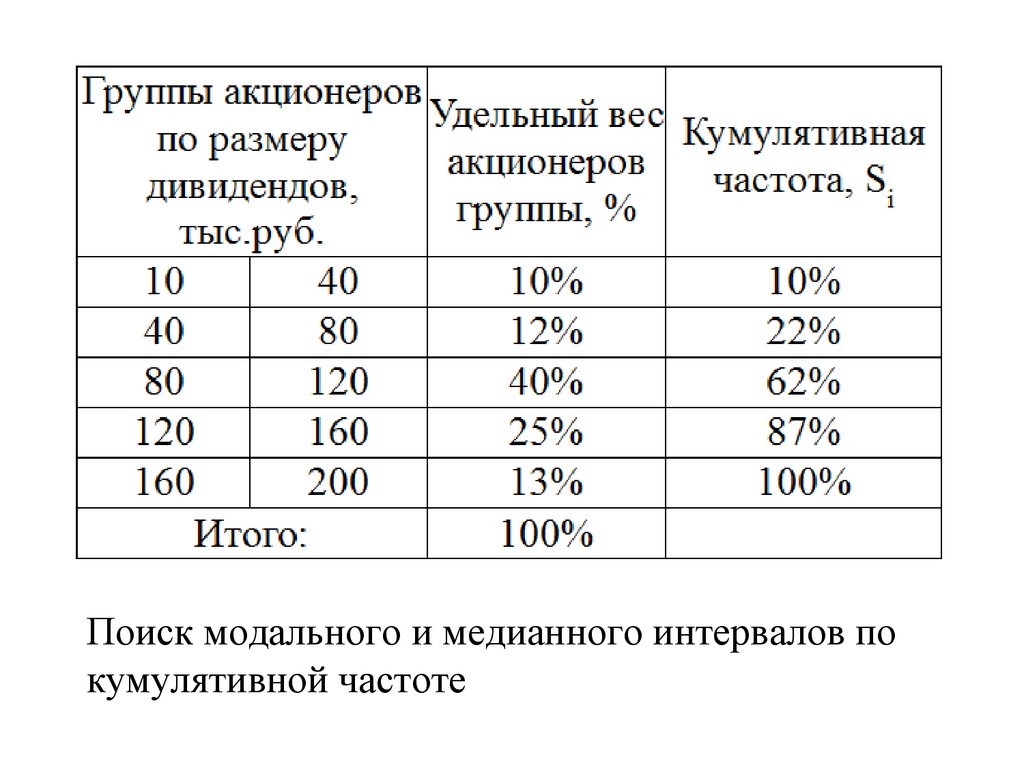
Поиск модального и медианного интервалов покумулятивной частоте
25.
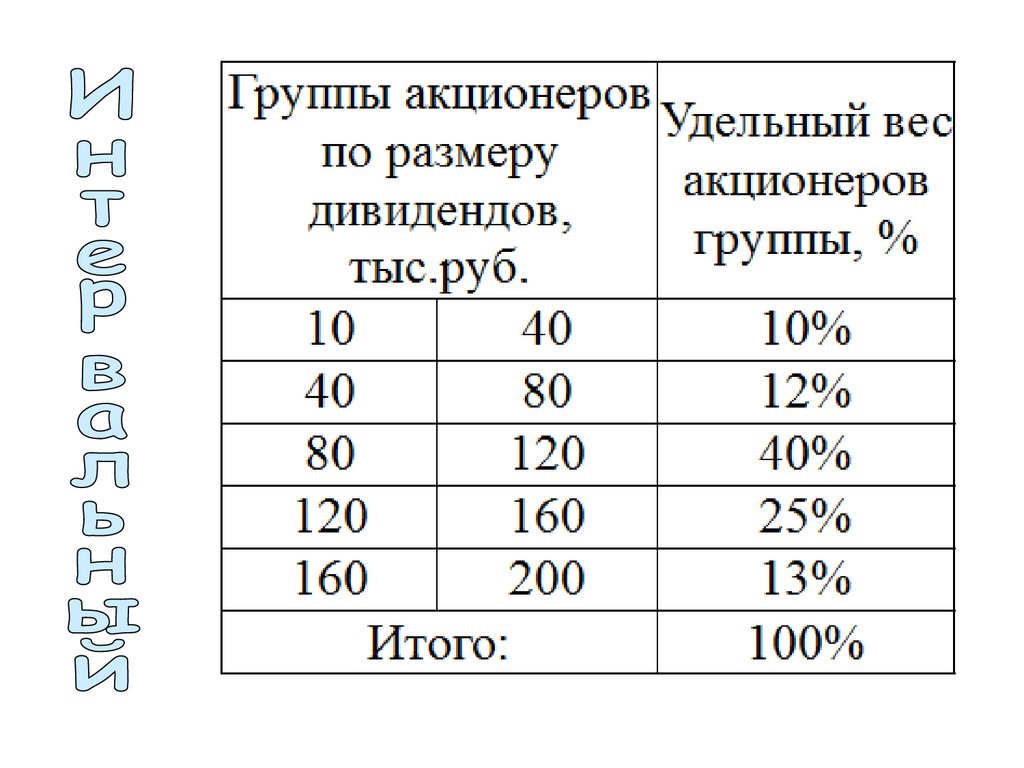
Гр у п п ы а кц и о н е р о в п оУд . в е с
р а з м е р у д и в и д е н то в ,
а кц и о н е р о в
т. р .
гр у п п ы %
10
40,0
10%
40,0
80,0
12%
80,0
120,0
40%
120,0
160,0
25%
160,0
200,0
13%
Ито го :
100%
Модальный и медианный интервалы
26.
40 12М о 80 (120 80 )
( 40 12 ) ( 40 25 )
106 , 05 т ы с.руб.
Большая часть акционеров имеет
размер дивидендов, близкий к
106050 руб.
27.
50 22М е 80 (120 80 )
40
108 т ы с.руб.
Половина акционеров имеет размер
дивидендов менее 108000 руб., а половина
более 108000 руб.
28.
ВЫВОДЫ:Мода и медиана описывают структуру
совокупности по изучаемому признаку;
Для первичного ряда моды и медианы не
существует;
Для ранжированного ряда существует
только медиана;
Для дискретного ряда мода и медиана конкретные значения признака, для
интервального мода и медиана
рассчитываются по формулам.
29.
Кафедра ЭКОНОМИКИМЕРЫ ВАРИАЦИИ
Астафурова И.С.
30.
КОМПЕТЕНЦИИ:В определении фактора и результата для
заданных показателей;
В выборе формулы для оценки вариации и
расчёте различных мер вариации,
необходимых для оценки влияния
признаков друг на друга и развёрнутой
оценке полученных результатов;
В графической иллюстрации выполненных
расчётов.
Астафурова И.С.
31. § 1.ОСНОВНЫЕ МЕРЫ ВАРИАЦИИ
Астафурова И.С.32.
Различие в значениях одногои того же признака у разных
единиц совокупности в один и
тот же момент времени,
возникающее в результате
разнообразных условий
(факторов)
Астафурова И.С.
33.
Размах;Среднее линейное отклонение;
Дисперсия;
Среднее квадратическое отклонение;
Коэффициент вариации
Астафурова И.С.
34.
R xmax xminРАЗМАХ ИЛИ
КОЛЕБЛЕМОСТЬ ПРИЗНАКА
Астафурова И.С.
35.
Данные о производительности трудапо двум магазинам коммерческого
предприятия (тыс.у.е./чел.)
1 отдел 2 отдел 3 отдел
магазин № 1
магазин № 2
9,5
7,5
10
10
КОЛЕБЛЕМОСТЬ R
для первого магазина - 1 тыс.у.е.;
для второго магазина - 5 тыс.у.е.
Астафурова И.С.
10,5
12,5
36.
КОЛЕБЛЕМОСТЬ может служитьбазой для расчёта возможных
резервах роста. Можно сделать
вывод о более устойчивой
производительности труда для
первого магазина, но достижения
второго магазина говорят о больших
возможностях к росту:
•для первого магазина самая высокая
производительность труда 10,5 тыс.у.е.;
•для второго магазина самая высокая
производительностьАстафурова
трудаИ.С.
12,5 тыс.у.е.
37.
Размах вариации показывает лишь крайниеотклонения признака и не отражает вариации
(отклонения) ВСЕХ вариантов в ряду. Для
отражения колебаний изменяющегося
(варьирующего) признака необходимы ещё
показатели и ЭТО
Астафурова И.С.
38. ОБОБЩЕНИЯ КОЛЕБАНИЙ ПРИЗНАКА
Среднее линейноеотклонение
Среднее квадратическое
отклонение
Астафурова И.С.
39.
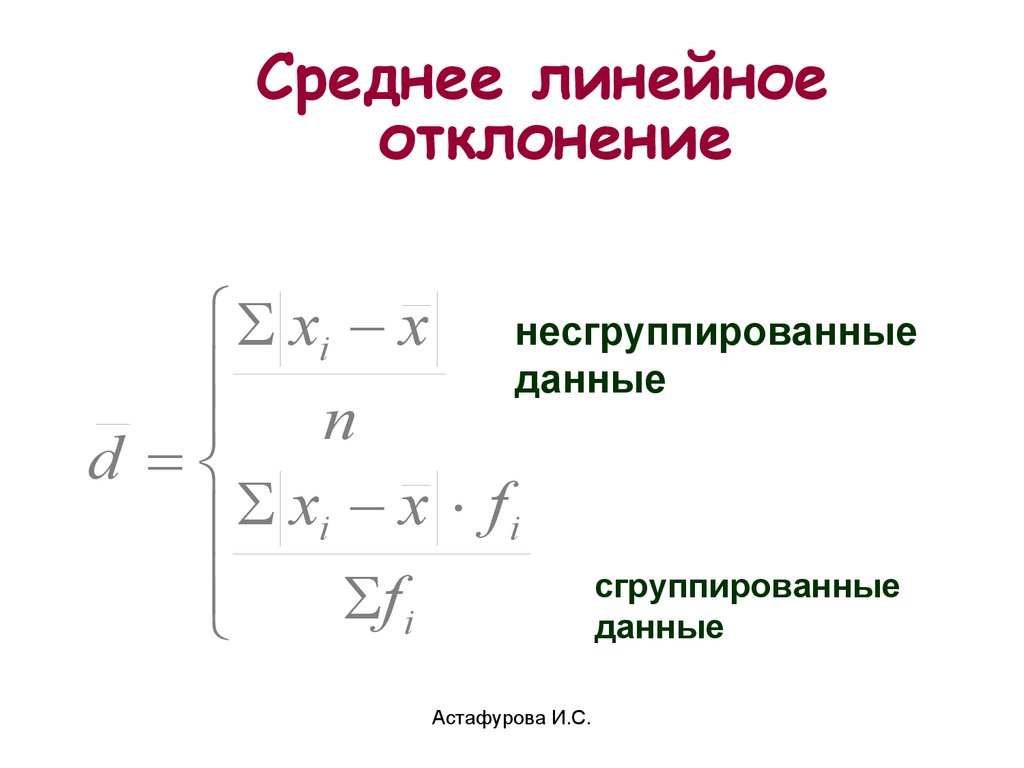
Среднее линейноеотклонение
xi x несгруппированные
данные
n
d
x
x
f
i
i
сгруппированные
f i
данные
Астафурова И.С.
40.
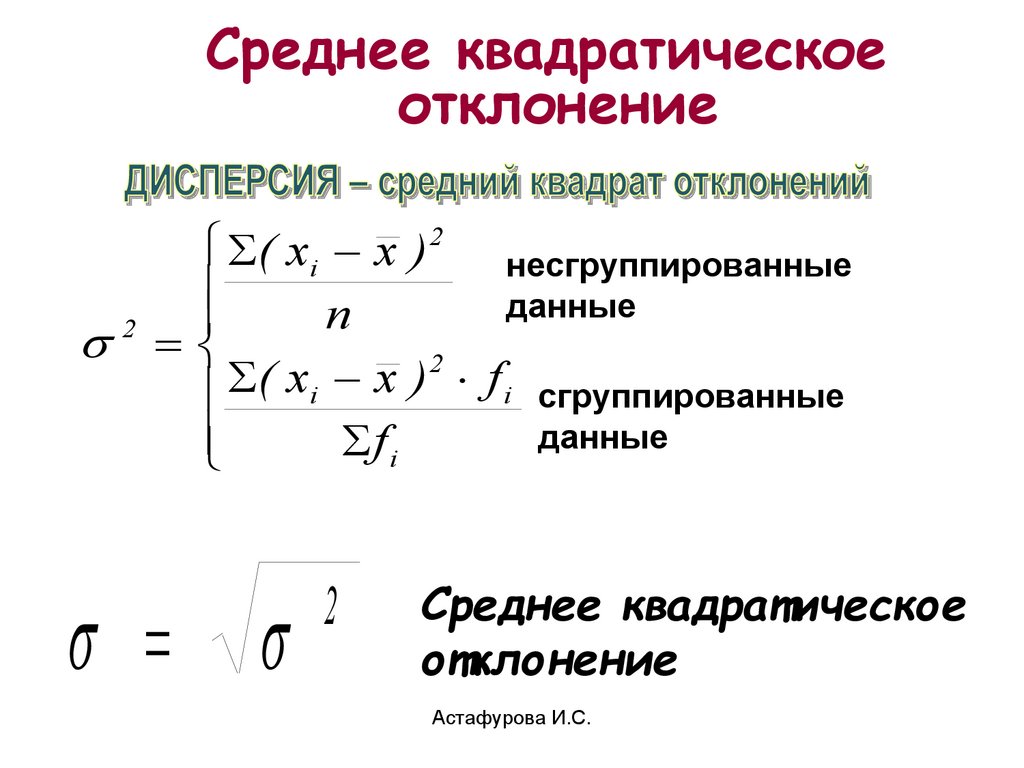
Среднее квадратическоеотклонение
( xi x )2 несгруппированные
данные
n
2
2
(
x
x
)
f i сгруппированные
i
данные
f
i
2
Среднее квадратическое
отклонение
Астафурова И.С.
41. СВОЙСТВА ДИСПЕРСИИ
1.Если к каждому значению признакаприбавить одно и тоже число, то
дисперсия не изменится:
2
[ ( x i A ) ( x A )] f i
2
fi
2. Если каждое значение признака
изменить в k раз, то дисперсия изменится в
2
раз:
k
2
[ ( x i k ) ( x k )] f i
2
2
k
fi
Астафурова И.С.
42.
Расчёт показателей по способумоментов (для интервальных
рядов с равными интервалами)
x fi
x
h A
fi
'
i
Астафурова И.С.
43.
Расчёт показателей по способумоментов (для интервальных
рядов с равными интервалами)
( x ) fi 2
2
h (x A)
fi
2
' 2
i
Астафурова И.С.
44.
Расчёт показателей по способумоментов (для интервальных
рядов с равными интервалами)
A - условный ноль (середина интервала с
максимальной частотой);
h - длина интервала;
x - середина i-го интервала.
i
Астафурова И.С.
45.
Коэффициент вариацииx
100% 33%
Астафурова И.С.
46.
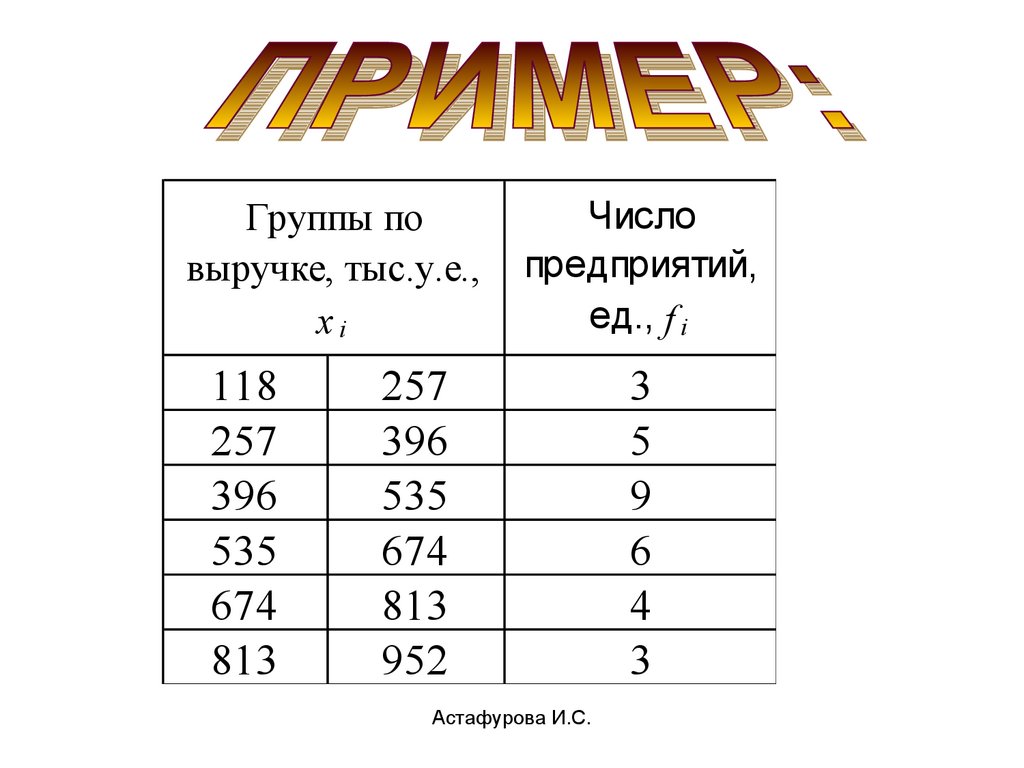
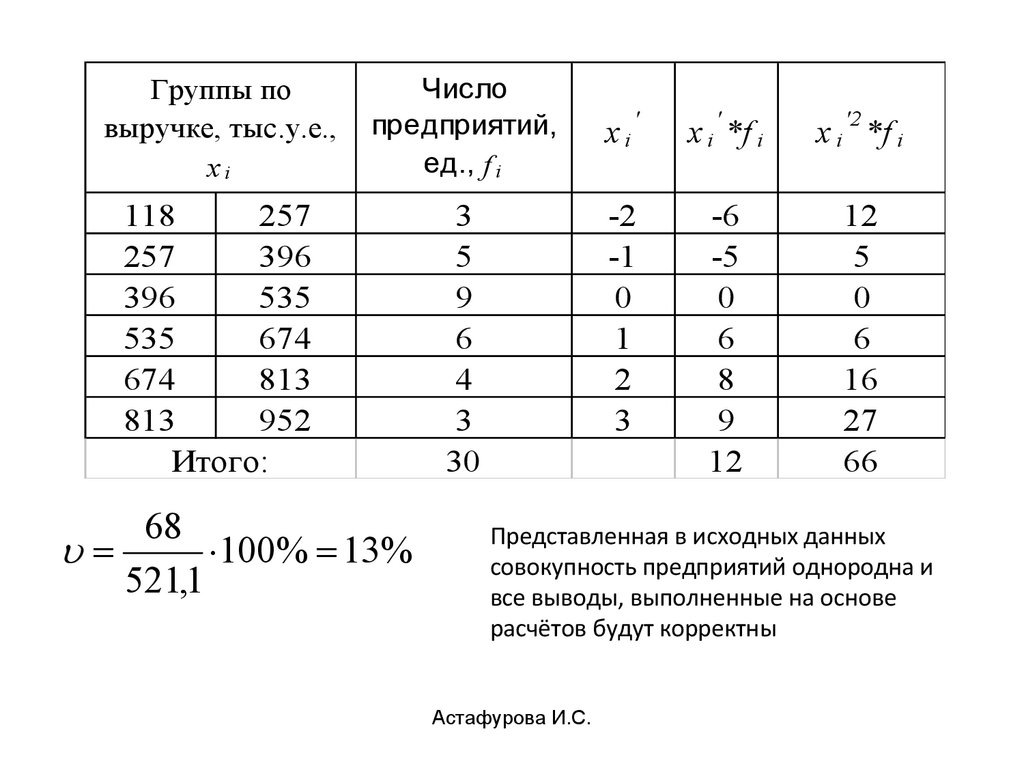
Группы повыручке, тыс.у.е.,
xi
118
257
396
535
674
813
Число
предприятий,
ед., f i
257
396
535
674
813
952
Астафурова И.С.
3
5
9
6
4
3
47.
Найти выручку в среднем наодно предприятие в секторе
экономики города и среднее
квадратическое отклонение
по способу моментов.
Астафурова И.С.
48.
Группы повыручке, тыс.у.е.,
xi
Число
предприятий,
ед., f i
118
257
257
396
396
535
535
674
674
813
813
952
Итого:
3
5
9
6
4
3
30
'
x i *f i
'
x i *f i
-2
-1
0
1
2
3
-6
-5
0
6
8
9
12
12
5
0
6
16
27
66
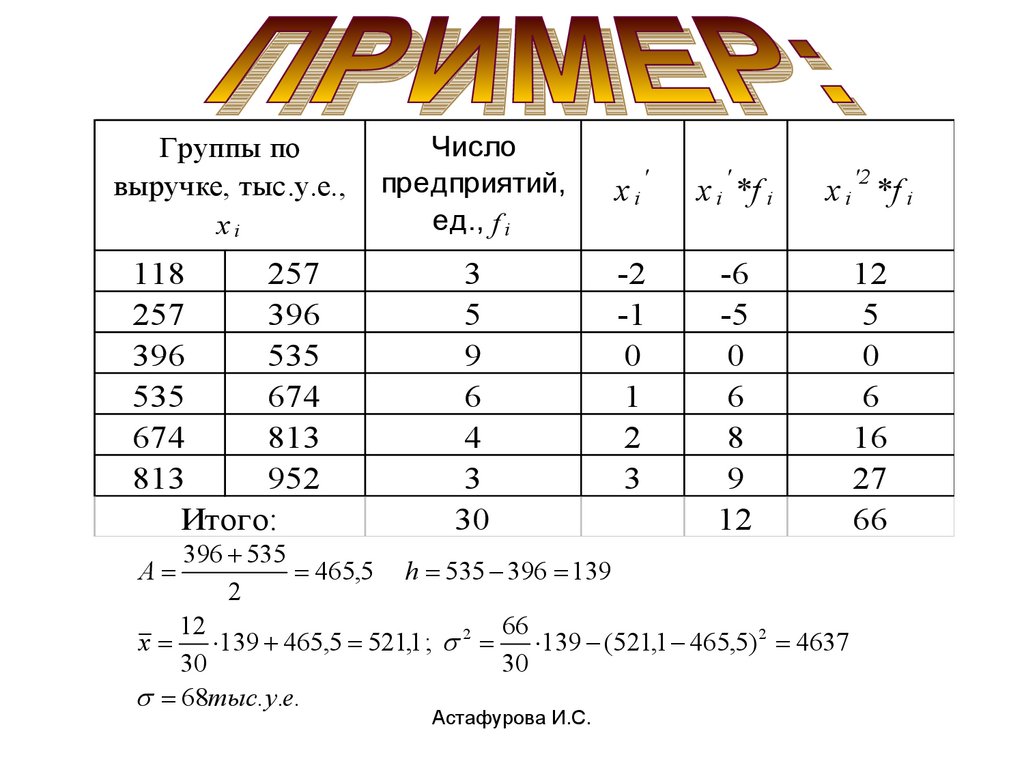
xi
396 535
465,5 h 535 396 139
2
12
66
x 139 465,5 521,1 ; 2 139 (521,1 465,5) 2 4637
30
30
68тыс. у.е.
A
Астафурова И.С.
'2
49.
Группы повыручке, тыс.у.е.,
xi
Число
предприятий,
ед., f i
118
257
257
396
396
535
535
674
674
813
813
952
Итого:
3
5
9
6
4
3
30
68
100% 13%
521,1
'
x i *f i
'
x i *f i
-2
-1
0
1
2
3
-6
-5
0
6
8
9
12
12
5
0
6
16
27
66
xi
'2
Представленная в исходных данных
совокупность предприятий однородна и
все выводы, выполненные на основе
расчётов будут корректны
Астафурова И.С.
50.
Средняя прибыль на однопредприятие составляет более 521
тысячи условных единиц, причём
отклонения выручки от её среднего
значения составляет довольно
большую величину – 68 тысяч
условных единиц
Астафурова И.С.
51.
1 - значение признака для единицсовокупности, обладающих изучаемым
свойством
0 - значение признака для единиц
совокупности, необладающих изучаемым
свойством
Астафурова И.С.
52.
р - доля единиц, обладающихизучаемым свойством
q - доля единиц,
необладающих изучаемым
свойством
Астафурова И.С.
53.
Астафурова И.С.54.
xi f ix
f i
1 p 0 q
p
p q
Астафурова И.С.
55.
2( xi x ) f i
f i
2
(1 p ) p (0 p ) q
p q
p q
2
2
Астафурова И.С.
56.
Налоговая инспекция проверила 100предпринимателей, у 25 были
обнаружены нарушения в расчётах по
налогам и сборам.
Определить:
-среднее число нарушений;
-среднее отклонение от среднего числа
нарушений.
Астафурова И.С.
57.
xi =1 для предпринимателей, укоторых были обнаружены
нарушения в расчётах по налогам и
сборам.
xi =0 для предпринимателей, у
которых не обнаружено
нарушений.
Астафурова И.С.
58.
доля предпринимателей, у которых былиобнаружены нарушения в расчётах по налогам и
сборам:
25
p
0.25
100
доля предпринимателей, у которых не
обнаружено нарушений:
75
q
0.75
100
Астафурова И.С.
59.
xi f ix
f i
1 25 0 75
0.25
100
Астафурова И.С.
60.
( x x ) ff
2
2
i
i
i
(1 0.25) 0.25 (0 0.25) 0.75
1
0.1875, 0.1875 0.43
2
2
Астафурова И.С.
61. § 2. ПРАВИЛО СЛОЖЕНИЯ ДИСПЕРСИЙ
Астафурова И.С.62.
ВАРИАЦИЯРазличие в значениях одного
и того же признака у разных
единиц совокупности в один и
тот же момент времени,
возникающее в результате
разнообразных условий
(факторов)
Астафурова И.С.
63.
Исследование вариациипозволяет её измерить,
выяснить причины,
выявить отдельные
факторы, влияющие на
результат для принятия
обоснованного решения.
Астафурова И.С.
64.
Влияние факторов можновыделить, произведя
группировку и оценив
влияние вариации фактора
группировки на изучаемый
признак, рассчитав три
вида дисперсий:
Астафурова И.С.
65.
Измеряет вариацию результата повсей совокупности под влиянием всех
факторов
Астафурова И.С.
66.
Характеризует систематическую вариациюрезультативного признака под влиянием
признака-фактора, положенного в основание
группировки
(xi x) fi
2
2
fi
Астафурова И.С.
67.
Отражает случайную вариацию результата подвлиянием неучтённых факторов
2
(
x
x
)
fi
дисперсия в i-ой
2
i
i
i
группе
fi
f i
f i
2
i
2
i
средняя из
внутригрупповых дисперсий
Астафурова И.С.
68.
22
Астафурова И.С.
2
i
69.
22
2
Астафурова И.С.
70.
Теснота связиВыражается в процентах: часть
изменений результата под влиянием
вариации фактора
Астафурова И.С.
71.
Астафурова И.С.72.
Сила связиПоказывает силу влияния фактора на результат по специальной шкале
Астафурова И.С.
73.
Астафурова И.С.74.
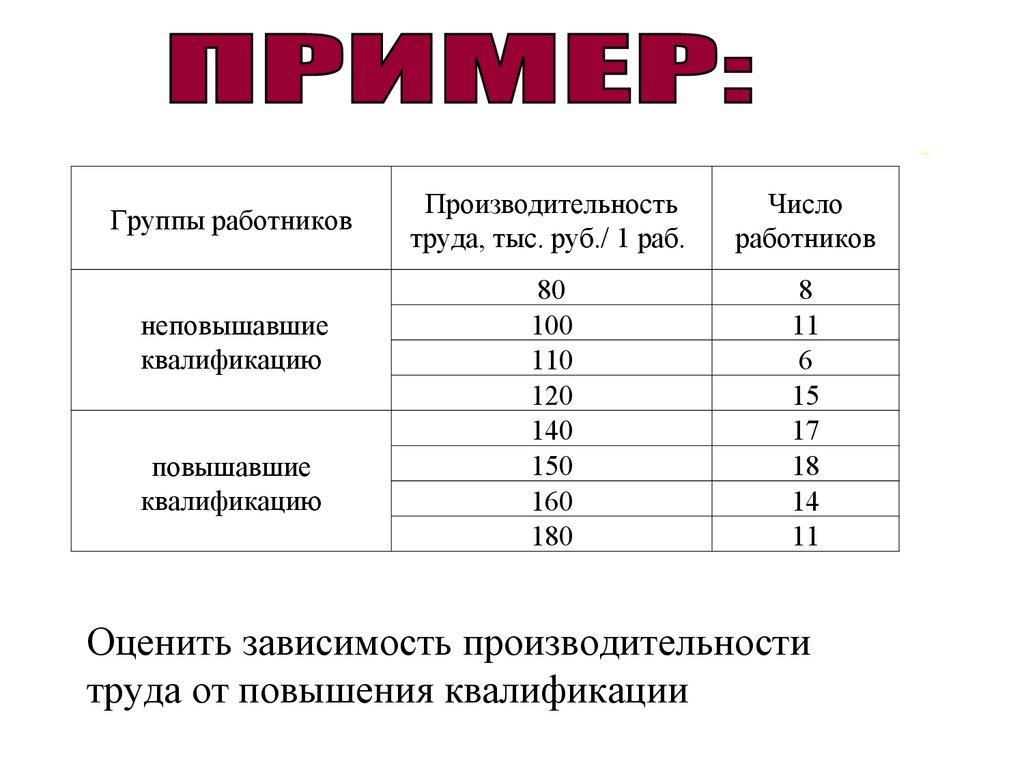
Группы работниковнеповышавшие
квалификацию
повышавшие
квалификацию
Производительность
труда, тыс. руб./ 1 раб.
Число
работников
80
100
110
120
140
150
160
180
8
11
6
15
17
18
14
11
Оценить зависимость производительности
труда от повышения квалификации
75.
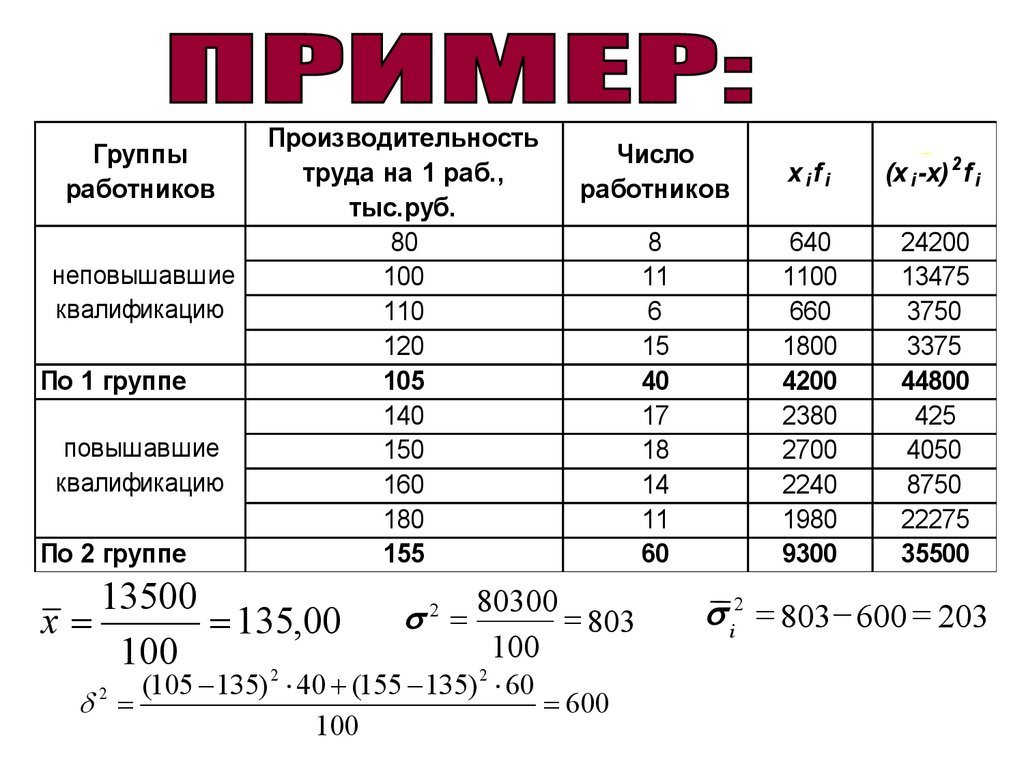
Группыработников
неповышавшие
квалификацию
По 1 группе
повышавшие
квалификацию
По 2 группе
Производительность
труда на 1 раб.,
тыс.руб.
80
100
110
120
105
140
150
160
180
155
13500
x
135,00
100
2
Число
работников
xifi
(x i -x) 2 f i
8
11
6
15
40
17
18
14
11
60
640
1100
660
1800
4200
2380
2700
2240
1980
9300
24200
13475
3750
3375
44800
425
4050
8750
22275
35500
2 80300 803
100
(105 135) 40 (155 135) 2 60
600
100
2
i2 803 600 203
76.
Для нашей задачи-эмпирический коэффициент
детерминации равен 600/803
=0,747, т.е. 74,7% изменений
производительности труда
зависит повышения
квалификации
эмпирическое корреляционное от
ношение-0,864
Астафурова И.С.
77.
x ; x•в интервале находится 68,3% единиц
совокупности
x
в интервале находится 95,4% единиц
x 2 ; x 2 •совокупности
x 2
в интервале находится 99,7% единиц
x 3 ; x 3 •совокупности
x 3
Астафурова И.С.
78. § 3. ПОКАЗАТЕЛИ АСИММЕТРИИ И ЭКСЦЕССА, ЦЕНТРАЛЬНЫЕ МОМЕНТЫ РАСПРЕДЕЛЕНИЯ
Астафурова И.С.79. © симметричным © асимметричным или скошенным.
© симметричным©
асимметричным или скошенным
.
80. Симметричный вариационный ряд
Симметричный вариационный ряд
• если частоты вариант по обе
стороны от центральной,
равноотстоящих от этого
значения, равны между собой
81. Асимметричный вариационный ряд
• частоты вариант по обестороны от центральной
изменяются неодинаково
82. Для расчета асимметрии используются центральные моменты
( m )которые рассчитываются по формуле:
(x i x ) fi
m
fi
m
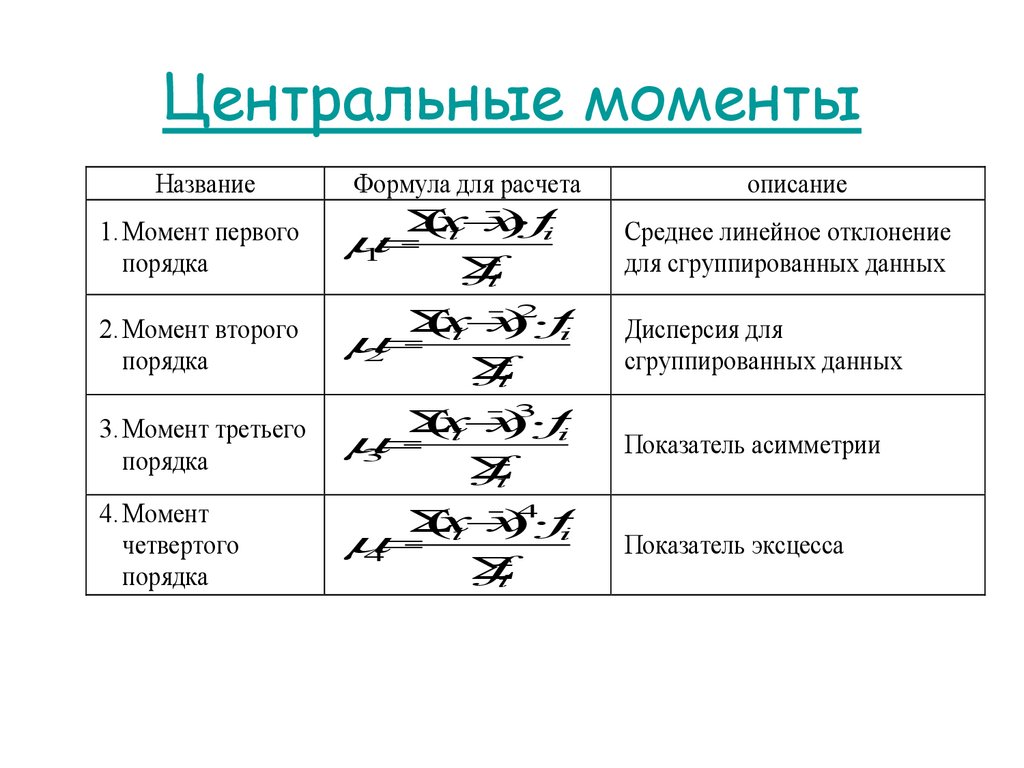
83. Центральные моменты
НазваниеФормула для расчета
описание
1. Момент первого
порядка
(x
x
) fi
i
1
fi
Среднее линейное отклонение
для сгруппированных данных
2. Момент второго
порядка
2
(x
x
)
fi
i
2
fi
Дисперсия для
сгруппированных данных
3. Момент третьего
порядка
3
(x
x
)
fi
i
3
fi
Показатель асимметрии
4. Момент
четвертого
порядка
4
(x
x
)
fi
i
4
fi
Показатель эксцесса
84.
центральный момент третьего порядка ( 3) используется для характеристикиасимметричности распределения (для симметричных распределений
( xi x ) 3 0 ), а степень асимметрии определяется с помощью коэффициента
асимметрии (А3): A3
3
.
3
Если А3=0, то говорят, что распределение симметрично, если А3>0, то
асимметрия является правосторонней, если А3<0, то асимметрия является
левосторонней.
Центральный момент четвертого порядка используется для оценки эксцесса
(остроты вершины распределения) на основе коэффициента эксцесса:
E 44 3 . Если E 0 , то распределение является нормальным, если E 0 ,
то ряд распределения является островершинным, а если E 0 , то –
плосковершинным.
85.
СилуСилу связи
связи между
между
признаками
признаками показывает
показывает
эмпирическое
эмпирическое корреляционное
корреляционное
отношение
отношение по
по шкале
шкале Чеддока
Чеддока;;
Эмпирический коэффициент
детерминации, выраженный в
процентах, показывает часть
вариации результативного
признака, зависящей от вариации
фактора
Астафурова И.С.
















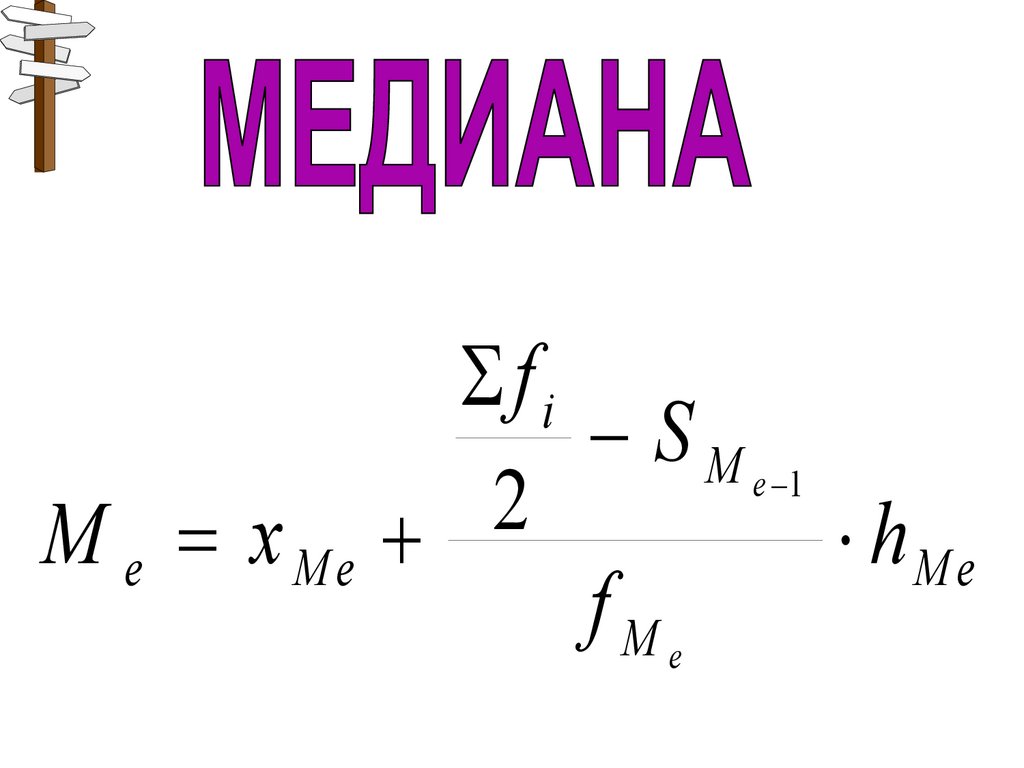



















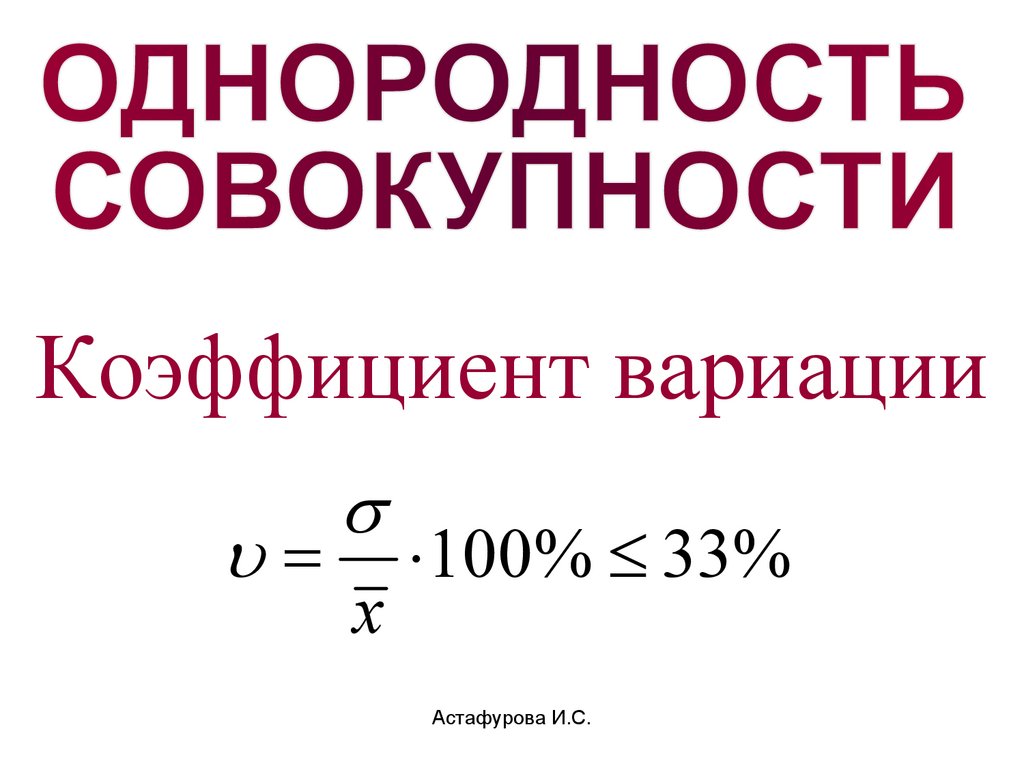





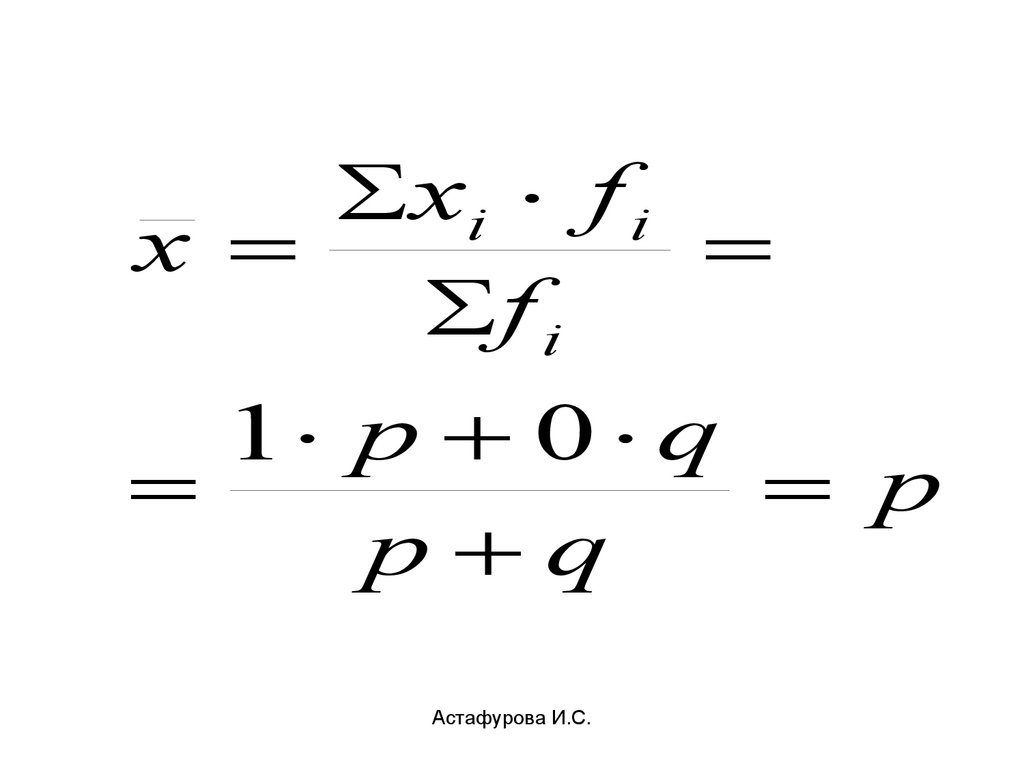
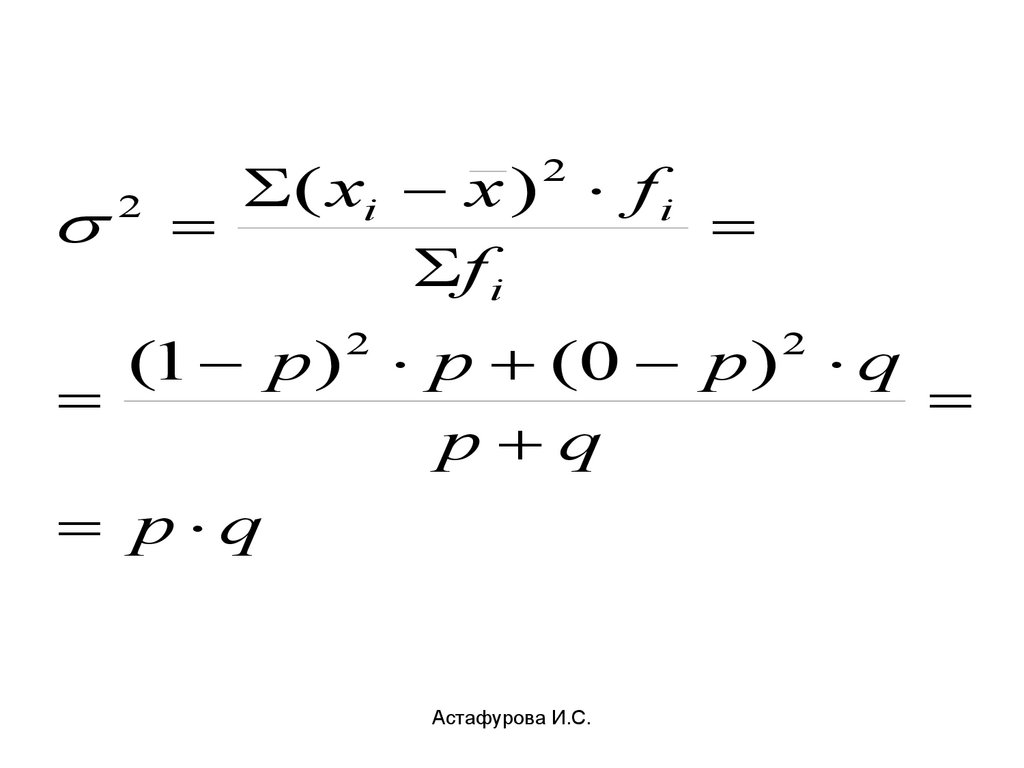



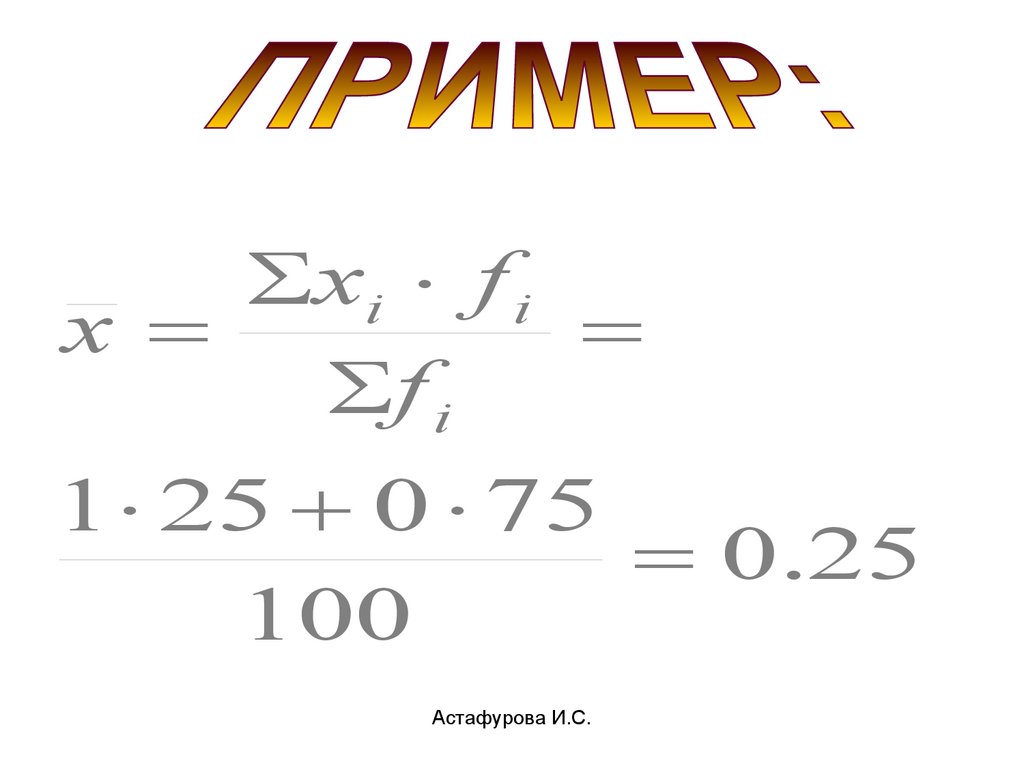























 mathematics
mathematics








