Соотношения между сторонами и углами прямоугольного треугольника (8 класс)

1. Геометрия 8 класс Соотношения между сторонами и углами прямоугольного треугольника

2. Оглавление

Синус, косинус и тангенс острого угла
прямоугольного треугольника
Основное тригонометрическое
тождество

3. Соотношения между сторонами и углами в прямоугольном треугольнике

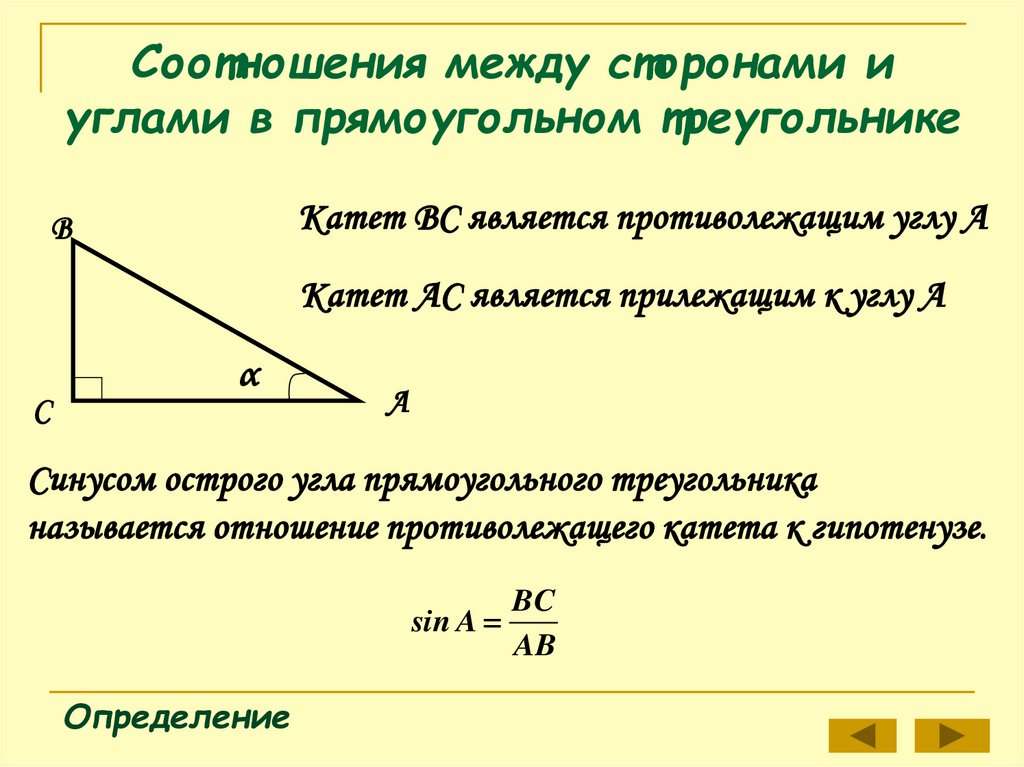
Катет ВС является противолежащим углу А
В
Катет АС является прилежащим к углу А
С
α
А
Синусом острого угла прямоугольного треугольника
называется отношение противолежащего катета к гипотенузе.
sin A
Определение
BC
AB

4. Соотношения между сторонами и углами в прямоугольном треугольнике

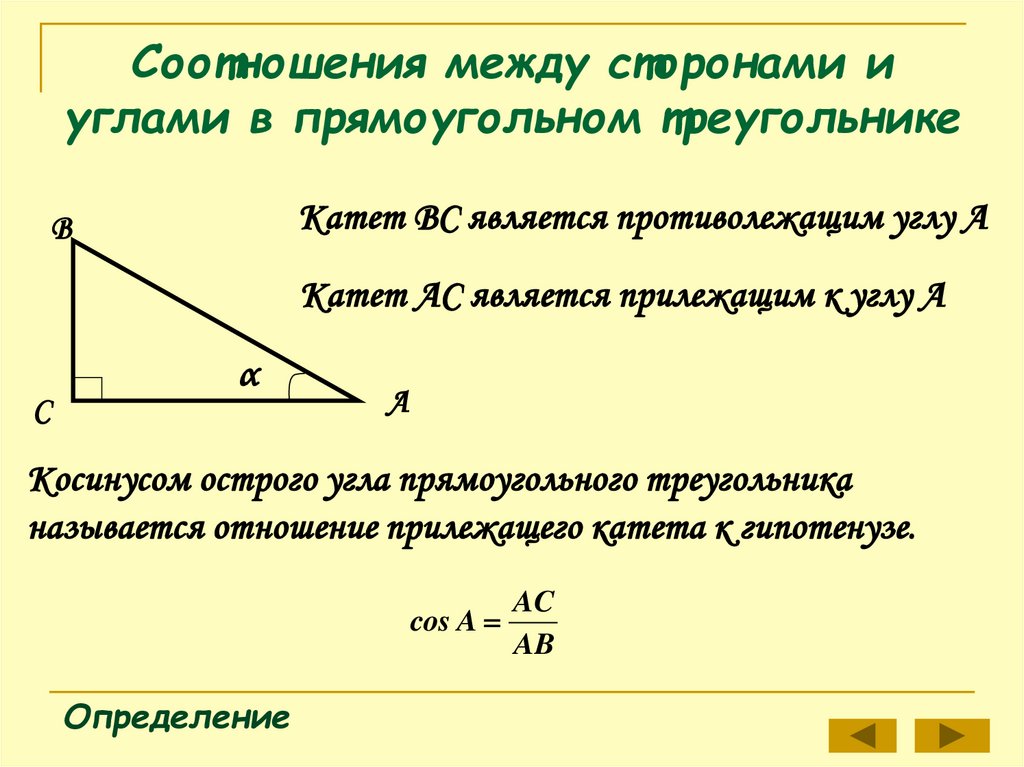
Катет ВС является противолежащим углу А
В
Катет АС является прилежащим к углу А
С
α
А
Косинусом острого угла прямоугольного треугольника
называется отношение прилежащего катета к гипотенузе.
cos A
Определение
AC
AB

5. Соотношения между сторонами и углами в прямоугольном треугольнике

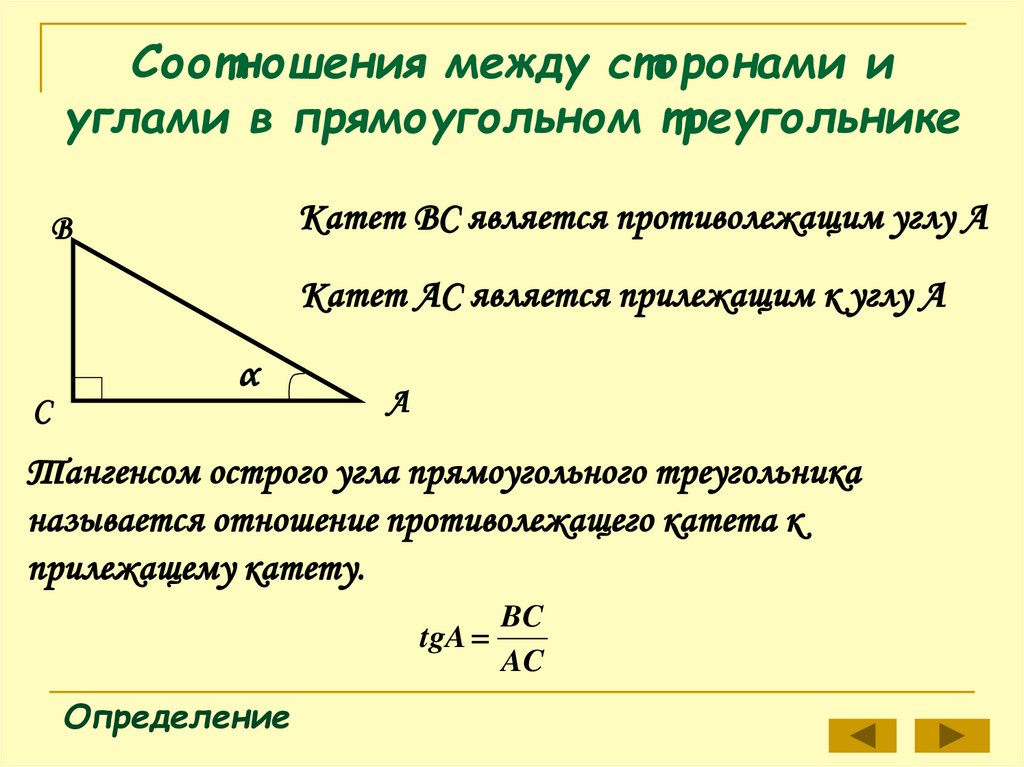
Катет ВС является противолежащим углу А
В
Катет АС является прилежащим к углу А
С
α
А
Тангенсом острого угла прямоугольного треугольника
называется отношение противолежащего катета к
прилежащему катету.
tgA
Определение
BC
AC

6. Соотношения между сторонами и углами в прямоугольном треугольнике

BC
sin A
AB
AC
cos A
AB
В
С
α
А
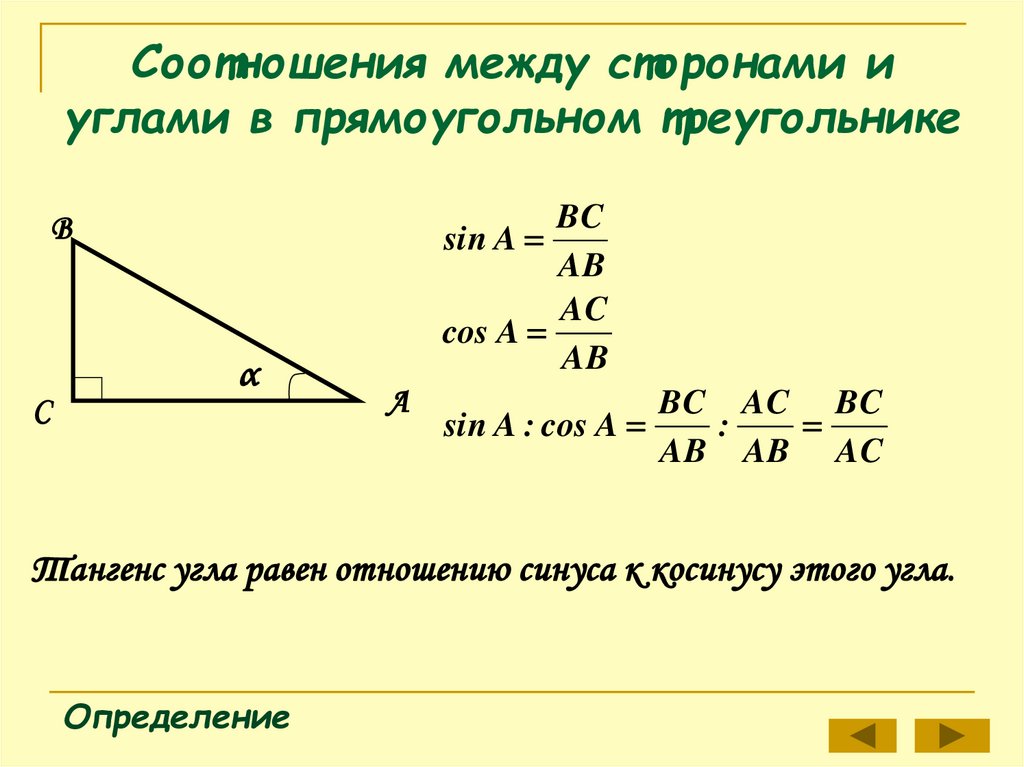
BC AC BC
sin A : cos A
:
AB AB AC
Тангенс угла равен отношению синуса к косинусу этого угла.
Определение

7. Соотношения между сторонами и углами в прямоугольном треугольнике

В1
В
С
α
α
А
С1
А1
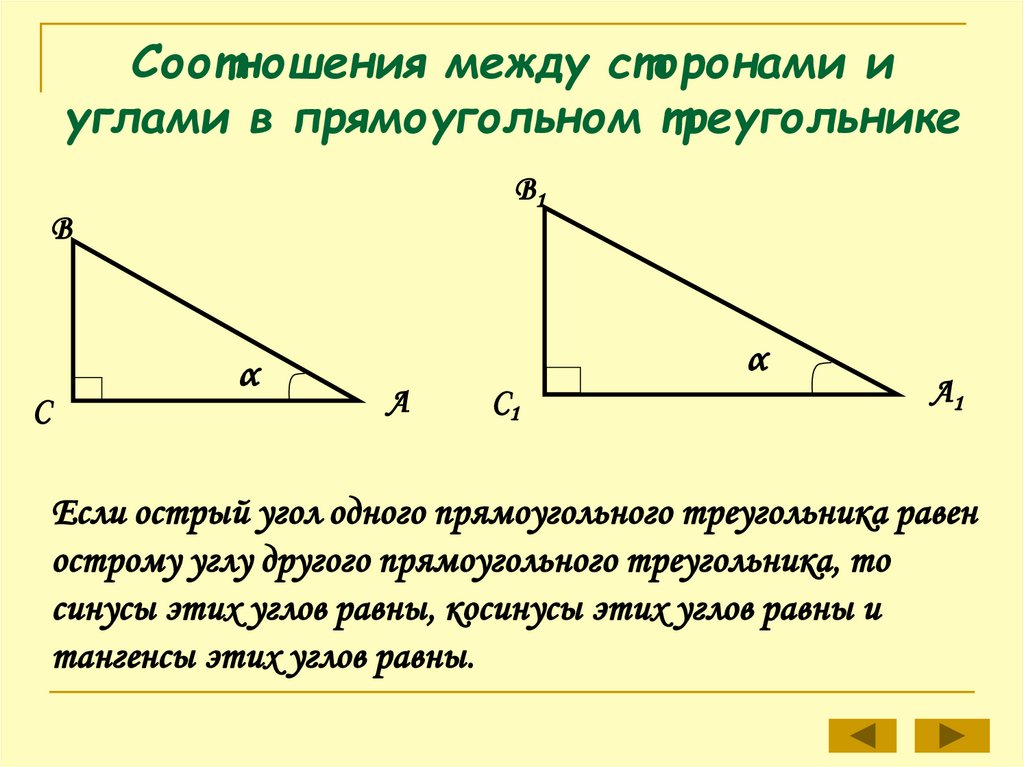
Если острый угол одного прямоугольного треугольника равен
острому углу другого прямоугольного треугольника, то
синусы этих углов равны, косинусы этих углов равны и
тангенсы этих углов равны.

8. Соотношения между сторонами и углами в прямоугольном треугольнике

С
ABC
В1
В
α
А С
AB
BC
AC
A1 B1 B1C 1 A1C 1
Таким образом,
Аналогично
~ A B C
А1
1
из равенства следует
sin A sin A1
, т.е.
BC B1C 1
, т.е.
AC A1C 1
1
1
(По I признаку подобия
треугольников )
α
AC A1C 1
AB A1 B1
1
cos A cos A1
tgA tgA1
BC B1C 1
AB A1 B1

9. Соотношения между сторонами и углами в прямоугольном треугольнике

sin 2 A cos 2 A 1
В
С
α
2
2
2
2
BC
AC
BC
AC
sin2 A cos 2 A
2
2
AB
AB
AB 2
А
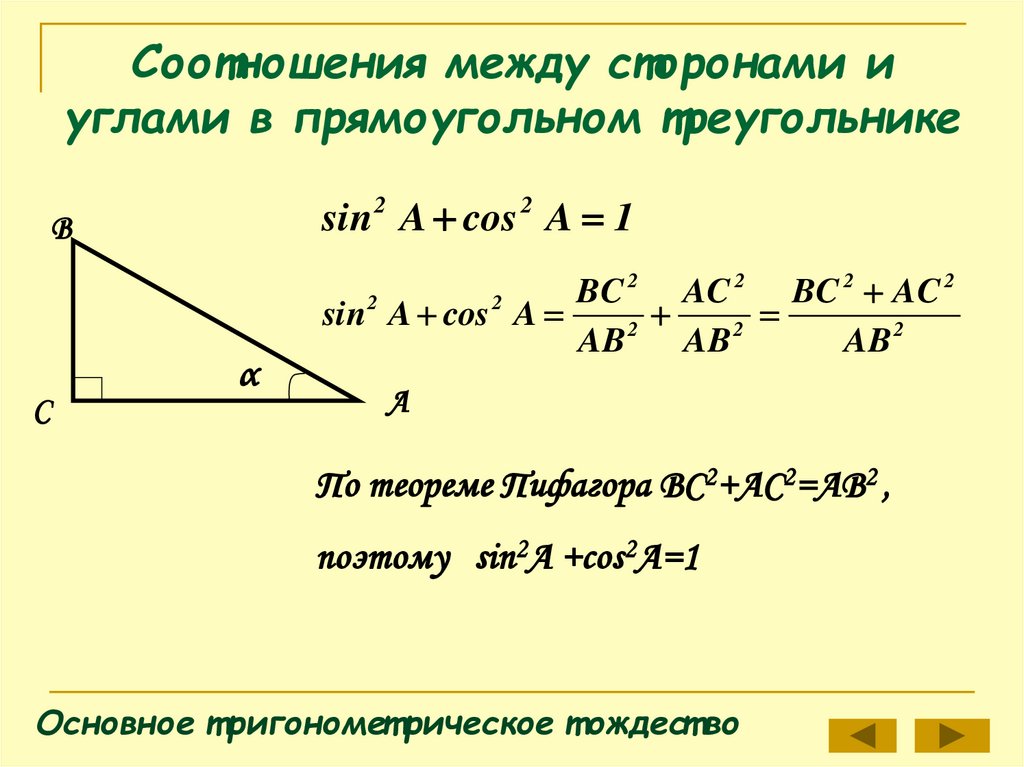
По теореме Пифагора ВС2+АС2=АВ2 ,
поэтому sin2A +cos2A=1
Основное т ригономет рическое т ождест во

10.

Литература
Л.С. Атанасян «Геометрия7-9» М., Просвещение,
2002.
Т.Л. Афанасьева, Л.А. Тапилина Геометрия. 8
класс: Поурочные планы по учебнику Л.С. Атанасяна
и др. «Геометрия7-9»