Численное дифференцирование

1.

Численное дифференцирование
Численное дифференцирование (ЧД) – метод нахождения производных
функции f(x), заданной значениями в узловых точках xi на отрезке [a,b].
В отличие от задачи численного интегрирования (ЧИ) задача ЧД не является
столь актуальной в связи с отсутствием принципиальных трудностей с аналитическим
нахождением производных.
ЧД применяется в следующих случаях:
при незнании аналитического вида функции f(x);
при сильном усложнении вида функции при ее аналитическом
дифференцировании (что затрудняет нахождение ее значений с высокой точностью);
при стремлении получения значений производных с помощью однотипных
вычислительных процессов без привлечения аналитических выкладок.
1

2.

Численное дифференцирование
Наиболее часто требуется вычислить первую и вторую производные функции f(x)
в определенных точках.
2 основных способа получения формул ЧД:
метод неопределенных коэффициентов (наиболее употребителен в
многомерном случае, когда не всегда просто выписывается интерполяционный
многочлен);
дифференцирование интерполяционных
получения простейших формул ЧД).
формул
(используется
для
2

3.

Метод неопределенных коэффициентов
Предположим, что формулы ЧД для производных k-го порядка имеют вид
f
(k )
n
( x) ci f xi ,
(1)
i 1
где
xi – узловые точки (узлы),
n – количество узловых точек,
ci – некоторые коэффициенты.
Определим коэффициенты ci, исходя из условия, чтобы формула была
точна для многочленов максимально высокой степени.
Возьмем
m
f ( x) a j x j .
j 0
Потребуем, чтобы для этой формулы соотношение (1) обратилось в равенство в
любой фиксированной точке x из отрезка [a,b]:
f
(k )
m
( x) a j x
j 0
j (k )
m
m n
j
ci f xi ci a j xi a j ci xij .
i 1
i 1 j 0
j 0 i 1
n
n
(2)
3

4.

Метод неопределенных коэффициентов
Чтобы (2) выполнялось для любого многочлена степени m, необходимо и
достаточно, чтобы коэффициенты при aj в обеих частях равенства (2) были
равны:
x ________________________ ci xij , j 0,1, , m.
j (k )
n
(3)
i 1
(3) - система линейных алгебраических уравнений (СЛАУ) относительно
вектора неизвестных ci, содержащая (m+1) уравнение с n неизвестными.
При m+1 = n основная матрица системы – квадратная, ее определитель –
определитель Вандермонда
________________________
4

5.

Метод неопределенных коэффициентов
Определитель Вандермонда не равен 0. Таким образом, всегда можно
построить формулу ЧД с n узлами, точную для многочленов степени m = n-1.
Кроме того, при m = n-1 и определенном расположении узлов иногда
оказывается, что (3) будет выполнено и при j = n. Как правило, это будет в
случае, когда узлы расположены симметрично относительно данной точки x, в
которой ищется производная.
При симметрично расположенных узлах справедливо следующее:
если порядок производной k – четное число, то
c1 = cn,
c2 = cn-1,…,
т.е. cn+1-k = ck;
если порядок производной k – нечетное число, то
c1 = -cn,
c2 = -cn-1,…,
т.е. cn+1-k = -ck.
Свойства симметрии формул ЧД используются для уменьшения числа
уравнений, которые нужно решить при построении формулы ЧД.
5

6.

Метод неопределенных коэффициентов
Пример 1. Построение формулы ЧД 1-го и 2-го порядков в центральном
узле для таблично заданной функции с симметрично расположенными 3 узлами
(рис. 1).
Рис. 1.
3 узла: n=3 – количество узлов, m=n-1=2 – степень многочлена.
1-я производная: k=1.
f’(x)=c1f(x-h)+c2f(x)+c3f(x+h).
6

7.

Метод неопределенных коэффициентов
Применяем формулу (3) для j=0,1,2, получаем
j 0 : x0 1 :
1
j 1: x x :
2
j 2:
x
:
1' 0 c1 c2 c3
x' 1 c1 ( x h) c2 x c3 ( x h)
x 2 ' 2 x c1 ( x h) 2 c2 x 2 c3 ( x h) 2
Учитывая, что узлы располагаются симметрично и k=1 – нечетное,
следует: c1=-c3.
Считая, что в качестве x можно взять любую точку, полагаем x=0:
0 c1 c2 c3
1 c1 ( h) c3 ( h)
0 c h2 c h2
1
3
7

8.

Метод неопределенных коэффициентов
Получаем:
f ' ( x)
f ( x h) f ( x h)
.
2h
(4)
2-я производная: k=2
f’’(x)=c1f(x-h)+c2f(x)+c3f(x+h).
Применяем формулу (3) для j=0,1,2, получаем
j 0 : x0 1 :
1
j 1: x x :
2
j 2:
x
:
1' ' 0 c1 c2 c3
x' ' 0 c1 ( x h) c2 x c3 ( x h) .
x 2 ' ' 2 c1 ( x h) 2 c2 x 2 c3 ( x h) 2
Учитывая, что узлы располагаются симметрично и k=2 – четное, следует: c1=c3.
Считая, что в качестве x можно взять любую точку, полагаем x=0:
8

9.

Метод неопределенных коэффициентов
0 c1 c2 c3
0 c1 ( h) c3 (h)
2 c h2 c h2
1
3
f ' ' ( x)
Получаем:
f ( x h) 2 f ( x ) f ( x h)
.
2
h
(5)
Формулы (4) и (5) – центральные формулы ЧД (центральные конечноразностные аппроксимации - КРА).
Аналогичным способом можно получить односторонние формулы ЧД для
1-й производной:
f ' ( x)
f ' ( x)
f ( x h) f ( x )
h
(для n=2)
f ( x 2 h) 4 f ( x h) 3 f ( x )
2h
(6)
(для n=3)
(7)
9

10.

Метод неопределенных коэффициентов
f ' ( x)
f ( x ) f ( x h)
h
f ' ( x)
3 f ( x ) 4 f ( x h) f ( x 2 h)
2h
(для n=2)
(8)
(для n=3)
(9)
Формулы (6) и (7) – правые КРА (формулы вперёд).
Формулы (8) и (9) – левые КРА (формулы назад).
10

11.

Дифференцирование интерполяционных форм
Интерполяционный многочлен Ньютона для неравноотстоящих узлов:
f ( x) Pn ( x) f ( x0 ) f ( x0 , x1 )( x x0 ) f ( x0 , x1 , x2 )( x x0 )( x x1 )
... f ( x0 , x1 ,..., xn )( x x0 )( x x1 ) ( x xn 1 ),
где f ( x0 , x1 ,..., xn )
– разделенная разность k-го порядка.
Тогда: f ( x) Pn ( x) f ( x0 ) f ( x0 , x1 ) 0 f ( x0 , x1 , x2 ) 0 1 ... f ( x0 , x1 ,..., xn ) 0 1 n 1
где
i x xi
Для 1-й производной:
f ' ( x) Pn ' ( x) f ( x0 , x1 ) f ( x0 , x1 , x2 ) 0 1 f ( x0 , x1 , x2 , x3 ) 0 1 0 2 1 2
Для 2-й производной:
f ' ' ( x) Pn ' ' ( x) 2 f ( x0 , x1 , x2 ) 2 f ( x0 , x1 , x2 , x3 ) 0 1 2
Общая формула имеет вид:
f
(k )
i k 1
k
( x) k! f ( x0 , x1 , , xk ) i f ( x0 , x1 , , xk 1 ) i j f ( x0 , x1 , , xk 2 )
i 0
i j 0
(10)
11

12.

Обрывая (10) на некотором числе членов, получаем формулу ЧД.
Если оставить в (10) только первый член, то
- для 1-й производной
- для 2-й производной
f ' ( x) f ( x0 , x1 )
f ( x1 ) f ( x0 )
;
x1 x0
f ( x2 ) f ( x1 ) f ( x1 ) f ( x0 )
f ( x1 , x2 ) f ( x0 , x1 )
x2 x1
x1 x0
f ' ' ( x) 2 f ( x0 , x1 , x2 ) 2
2
.
x2 x0
x2 x0
Последние формулы рассчитаны на произвольную неравномерную сетку.
При использовании равномерной сетки формулы упрощаются.
При
xi 1 xi h получаем:
f ' ( x) f ( x0 , x1 )
f ( x1 ) f ( x0 )
,
h
что совпадает с полученными ранее формулами (6), (8) при соответствующем выборе
x.
f ( x2 ) f ( x1 ) f ( x1 ) f ( x0 )
f ( x2 ) 2 f ( x1 ) f ( x0 )
h
h
f ' ' ( x) 2
,
2h
h2
что совпадает с полученной ранее формулой (5) при x x1.
12

13.

Оценка погрешности численного дифференцирования
Для оценки погрешности формул ЧД можно использовать представление
функции в виде формулы Тейлора. При этом исходная функция считается
достаточно гладкой для наличия производных соответствующего порядка.
Введем обозначение для погрешности формулы ЧД:
Оценим погрешность (6):
f ' ( x)
Rk ( f ) f
(k )
n
( x) ci f xi .
i 1
f ( x h) f ( x )
.
h
Формула Тейлора с остаточным членом в форме Лагранжа:
f ( x h) ___________________, d x, x h .
Получаем:
h2
f ( x) hf ' ( x)
f ' ' (d ) f ( x)
f ( x h) f ( x )
2
R1 ( f ) f ' ( x)
f ' ( x)
______ O(h)
h
h
- формула 1-го порядка точности.
Оценим погрешность (4):
f ' ( x)
f ( x h) f ( x h)
.
2h
13

14.

Оценка погрешности численного дифференцирования
Формула Тейлора с остаточным членом в форме Лагранжа:
h2
h3
f ( x h) f ( x) hf ' ( x)
f ' ' ( x)
f ' ' ' (d1 ), d1 x, x h ,
2
6
h2
h3
f ( x h) f ( x) hf ' ( x)
f ' ' ( x)
f ' ' ' (d 2 ), d 2 x h, x .
2
6
f ( x h) f ( x h)
f ' ( x)
2h
h2
h3
h2
h3
f ( x) hf ' ( x)
f ' ' ( x)
f ' ' ' (d1 ) f ( x) hf ' ( x)
f ' ' ( x)
f ' ' ' (d 2 )
2
6
2
6
R1 ( f ) f ' ( x)
2h
2
2
h f ' ' ' (d1 ) f ' ' ' (d 2 )
h
h2
f ' ' ' (d ) O(h 2 ),
6
2
6
6
f ' ' ' (d1 ) f ' ' ' (d 2 )
f ' ' ' (d1 ), f ' ' ' (d 2 ) .
2
Получилась формула 2-го порядка точности.
где
14

15.

Оценка погрешности численного дифференцирования
Оценим погрешность (5):
f ' ' ( x)
f ( x h) 2 f ( x ) f ( x h)
.
2
h
Аналогично рассмотренному получаем:
h2
R2 ( f )
f ' ' ' ' (d ) O(h 2 )
12
- формула 2-го порядка точности.
При вычислении одной и той же величины формулы с большим количеством узлов
дают более высокий порядок точности, но они более громоздки.
Остаточные члены формул ЧД выражаются через производные более высоких
порядков, поэтому в чистом виде они малопригодны для практического оценивания.
Однако:
1. Они важны для качественного оценивания различных аппроксимаций
производных.
2. Можно оценивать порядок производной, принимая max | f ( n 1) ( x) | величину
max | f ( x0 , x1 ,..., xn 1 ) |.
3. Аппроксимация производных по равномерной сетке позволяет использовать
принцип Рунге двойного счета с разными шагами подобно тому, как это делалось при
вычислении определенных интегралов.
15

16.

Оценка погрешности численного дифференцирования
Если f(x,h) – значение некоторой производной, вычисленной с шагом h с помощью
формулы ЧД порядка точности p, то f(x,2h) – с шагом 2h. Пересчет оценки
производной выполняется по формуле:
f ( n ) ( x ) f ( x, h )
Оценка точности:
f ( x, h ) f ( x, 2 h )
.
p
2 1
f ( x, h ) f ( x, 2 h )
.
2 p 1
Расчет начинается с вычисления при минимальном шаге h, затем он удваивается
(увеличивается).
Тем не менее, истинная ошибка, как правило, превосходит все приведенные оценки
точности. Это связано с влиянием погрешности округлений исходных данных.
16

17.

Вычислительная погрешность формул ЧД. Оптимизация шага ЧД
При ЧД приходится вычитать друг из друга близкие значения функции. Это приводит
к уничтожению первых значащих цифр, т.е. к потере достоверных знаков числа. Если
значения функции известны с малой точностью, неизвестно, останется ли в ответе
хоть один достоверный знак.
Часто уменьшение погрешности формулы ЧД сопровождается ростом влияния
погрешности исходных данных и, как следствие, ростом вычислительной
погрешности. Влияние этих погрешностей сказывается уже при умеренных
значениях погрешности метода решения задачи.
Рассмотрим соотношение (6):
Остаточный член для этой формулы
Тогда:
f ' ( x)
R1 ( f )
h
f ' ' (d )
2
f ( x h) f ( x ) h
f ' ' (d )
h
2
17

18.

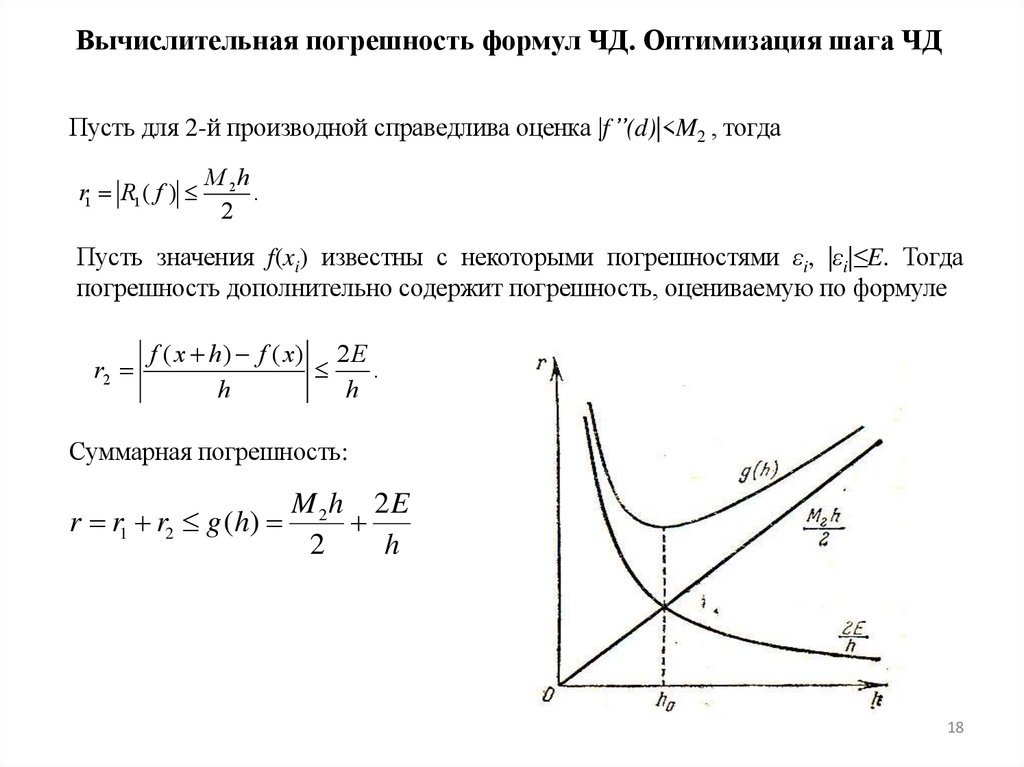
Вычислительная погрешность формул ЧД. Оптимизация шага ЧД
Пусть для 2-й производной справедлива оценка |f’’(d)|<M2 , тогда
r1 R1 ( f )
M 2h
.
2
Пусть значения f(xi) известны с некоторыми погрешностями εi, |εi|≤E. Тогда
погрешность дополнительно содержит погрешность, оцениваемую по формуле
r2
f ( x h) f ( x ) 2 E
.
h
h
Суммарная погрешность:
r r1 r2 g (h)
M 2h 2E
2
h
18

19.

Вычислительная погрешность формул ЧД. Оптимизация шага ЧД
Точка экстремума определяется из НУО:
h2
h0 2
Оптимальный шаг:
g ' ( h)
M 2 2E
2 0.
2
h
4E
M2
E
.
M2
g (h0 ) 2 M 2 E
Величина погрешности:
В лучшем случае значения функции по точности ограничены разрядностью m
мантиссы машинного числа. В этом случае E 2 m
Тогда
g (h0 ) const 2
m
2
Т.о. f’(x) можно получить в лучшем случае с половиной верных (двоичных)
разрядов.
19

20.

Вычислительная погрешность формул ЧД. Оптимизация шага ЧД
Для формул ЧД более высоких порядков точности ситуация с погрешностью
несколько лучше. Например, для центральной КРА (4), если |f’’’(d)|<M3 :
M 3h 2 E
g ( h)
6
h
Оптимальный шаг:
Если
E 2
m
, то
h0 3
3E
M3
3
m
h0
2 3
M3
3
g (h0 ) const 2
2 m
3
Т.о. сохраняется 2/3 разрядов.
20

21.

Вычислительная погрешность формул ЧД. Оптимизация шага ЧД
Для (5), если |f’’’’(d)|<M4 :
M 4h2 4E
g ( h)
2
12
h
M 4h2 4E
g ( h)
2
12
h
Оптимальный шаг:
h0 24
Если
E 2 m
, то
3E
M4
3
m
h0 24
2 4
M4
g (h0 ) const 2
m
2
Т.о. опять сохраняется половина разрядов.
21

22.

Вычислительная погрешность формул ЧД. Оптимизация шага ЧД
В стандартах IEEE 754 для работы с числами с плавающей запятой
(основание = 2) длина мантиссы
- для одинарной точности (float) m = 24,
- для одинарной расширенной точности (double) m = 32
Алгоритм. Алгоритм для расчета машинного эпсилон ε и длины мантиссы m:
ε :=1.0;
m:=1;
while (1+ ε >1) do
begin
ε := ε /2;
m:=m+1;
end;
22