Similar presentations:
Численное дифференцирование и интегрирование (тема 6,7)
1. Тема 6 и 7 Численное дифференцирование и интегрирование
«Вычислительная математика»Тема 6 и 7
Численное
дифференцирование и
интегрирование
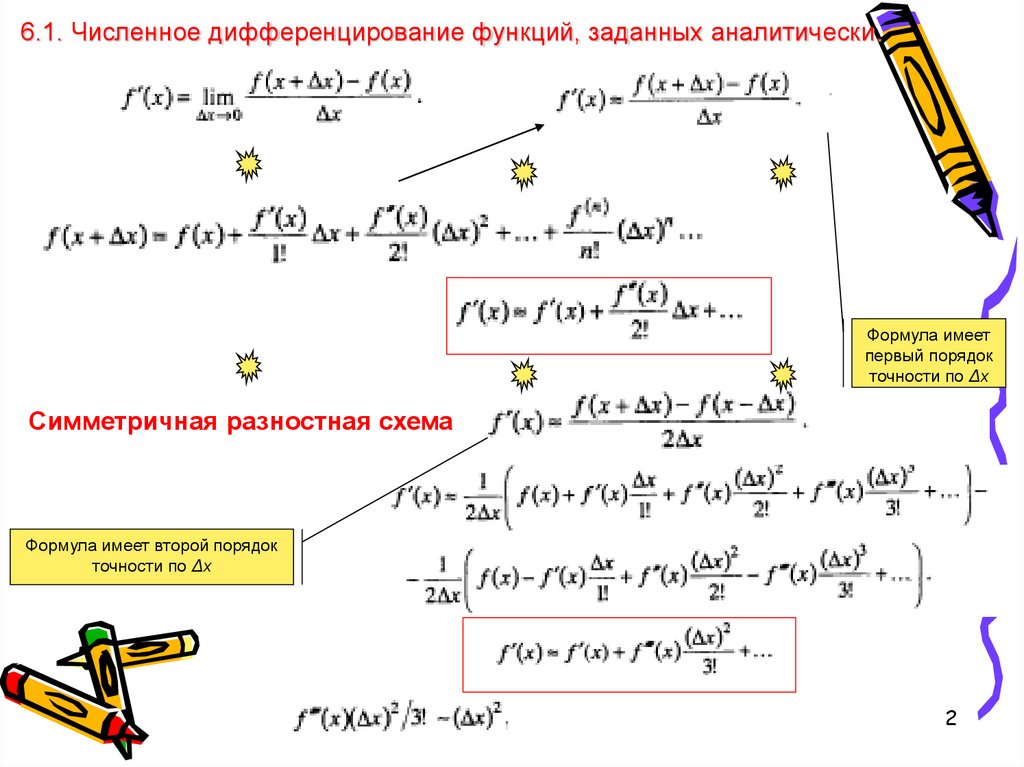
6.1. Численное дифференцирование функций, заданных аналитически.
6.2. Численное интегрирование
2.
6.1. Численное дифференцирование функций, заданных аналитически.Формула имеет
первый порядок
точности по Δх
Симметричная разностная схема
Формула имеет второй порядок
точности по Δх
2
3.
6.2. Численное дифференцирование функций, заданных таблично.Пусть известны табличные значения функции f(x) в конечном числе
точек отрезка [а,в]. Требуется определить значение производной в
некоторой точке отрезка [а,в].
Интерполяция - способ вычислить промежуточное значение функции по
нескольким уже известным ее значениям.
Например: Имеется функция f(x), известны
результаты значения f(x) в точке x0 и точке x2,
интерполяця помогает найти значение f(x1) при
условии что x1 принадлежит интервалу от x0 до x2.
6000 15.5
6378
Метод "линейная интерполяция“:
?
8000 19.2
Если x1 лежит вне интервала (x0, x2), то нужно
использовать "экстраполяцию".
3
4.
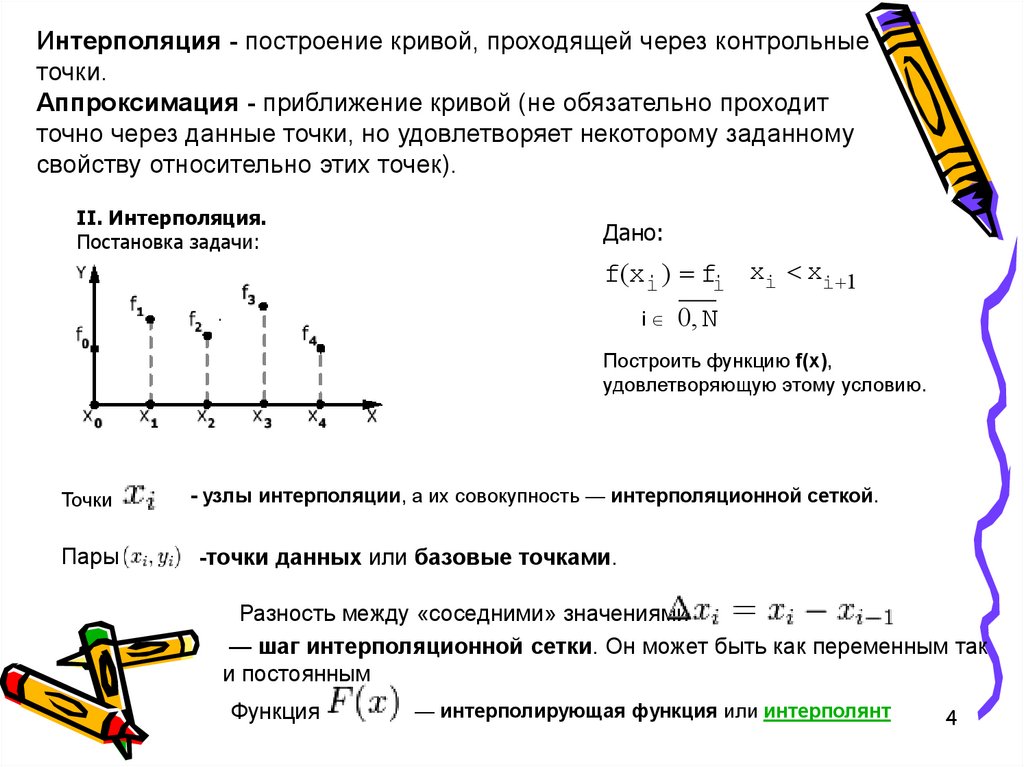
Интерполяция - построение кривой, проходящей через контрольныеточки.
Аппроксимация - приближение кривой (не обязательно проходит
точно через данные точки, но удовлетворяет некоторому заданному
свойству относительно этих точек).
II. Интерполяция.
Постановка задачи:
Дано:
f(xi ) fi xi xi 1
i 0, N
.
Построить функцию f(x),
удовлетворяющую этому условию.
Точки
- узлы интерполяции, а их совокупность — интерполяционной сеткой.
Пары
-точки данных или базовые точками.
Разность между «соседними» значениями
— шаг интерполяционной сетки. Он может быть как переменным так
и постоянным
Функция
— интерполирующая функция или интерполянт
4
5.
1) Кусочно-постоянная интерполяцияДля левой кусочно-линейной интерполяции
Для правой кусочно-линейной интерполяции
5
6.
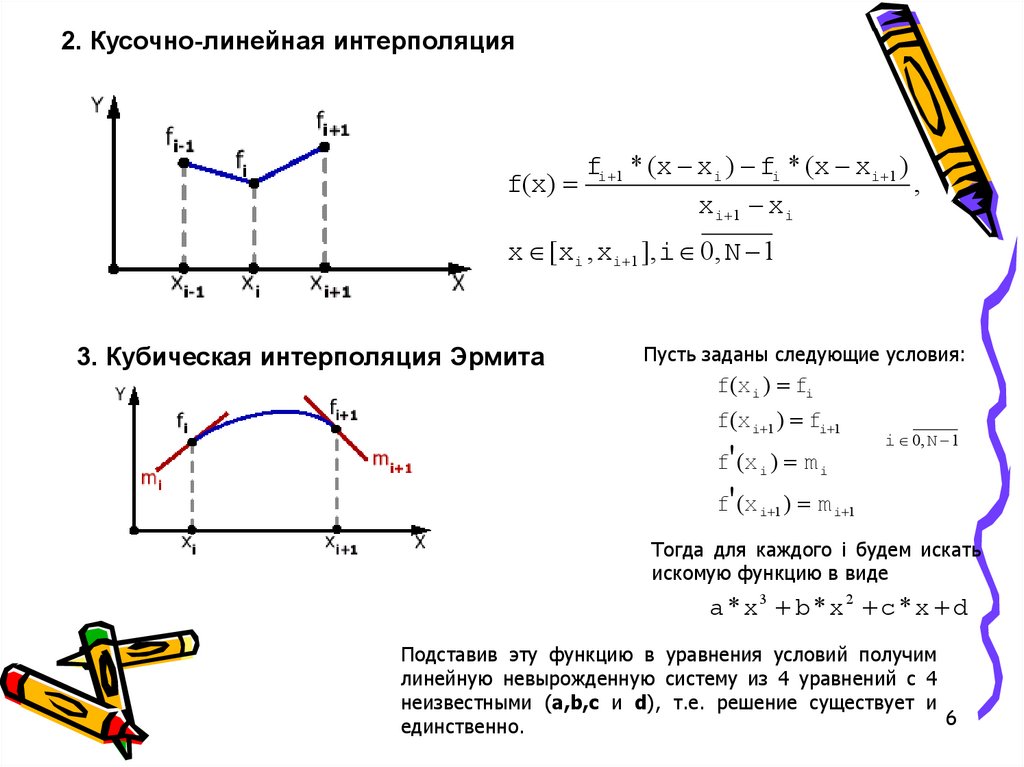
2. Кусочно-линейная интерполяцияf(x)
fi 1 * (x xi ) fi * (x xi 1 )
,
xi 1 xi
x [xi , xi 1 ], i 0, N 1
3. Кубическая интерполяция Эрмита
Пусть заданы следующие условия:
f(xi ) fi
f(xi 1 ) fi 1
f' (xi ) m i
i 0, N 1
f' (xi 1 ) m i 1
Тогда для каждого i будем искать
искомую функцию в виде
a * x3 b * x 2 c * x d
Подставив эту функцию в уравнения условий получим
линейную невырожденную систему из 4 уравнений с 4
неизвестными (a,b,c и d), т.е. решение существует и
6
единственно.
7.
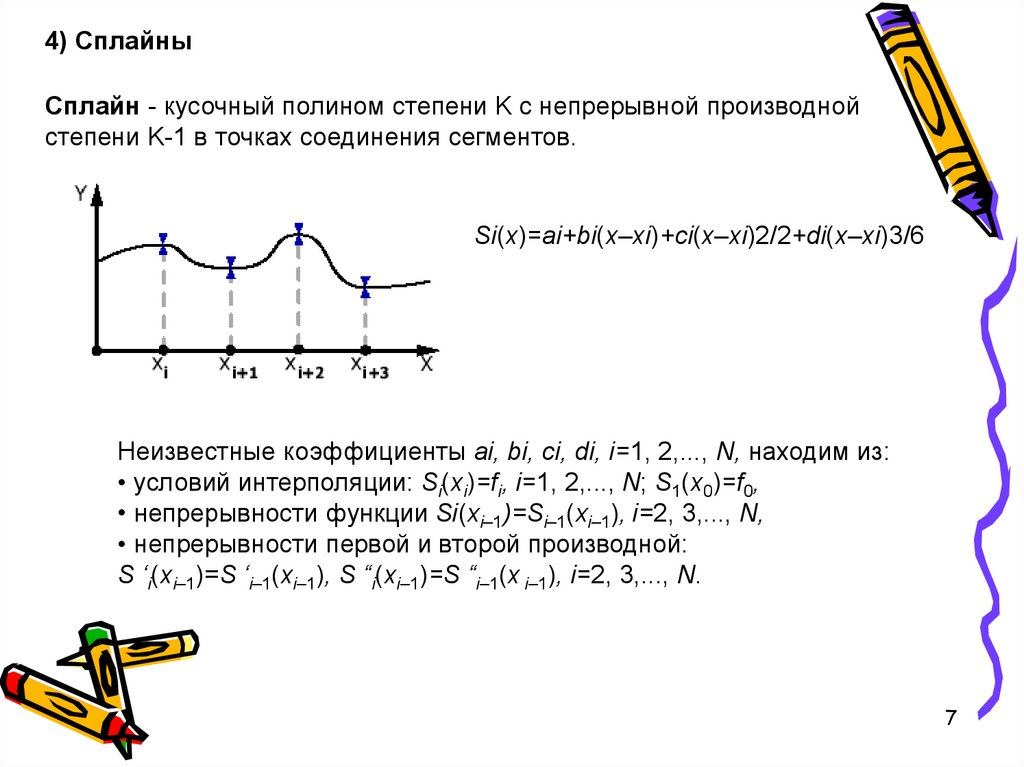
4) СплайныСплайн - кусочный полином степени K с непрерывной производной
степени K-1 в точках соединения сегментов.
Si(x)=ai+bi(x–xi)+ci(x–xi)2/2+di(x–xi)3/6
Неизвестные коэффициенты ai, bi, ci, di, i=1, 2,..., N, находим из:
• условий интерполяции: Si(xi)=fi, i=1, 2,..., N; S1(x0)=f0,
• непрерывности функции Si(xi–1)=Si–1(xi–1), i=2, 3,..., N,
• непрерывности первой и второй производной:
S ‘i(xi–1)=S ‘i–1(xi–1), S “i(xi–1)=S “i–1(x i–1), i=2, 3,..., N.
7
8.
89.
910.
АППРОКСИМАЦИЯ ПРОИЗВОДНЫХ КОНЕЧНЫМИ РАЗНОСТЯМИy
,
x 0 x
y f (x) lim
y f (x x) f (x).
y
y
x
Вычисление производной y i в точке xi
1) левой разности:
Оценка погрешности
y y i y i 1 y i y i 1
;
x x i x i 1
h
y i
y i y i 1
0(h ),
h
y y i 1 y i y i 1 y i
y i
;
x x i 1 x i
h
y i
y i 1 y i
0(h ),
h
y i
2) правой разности:
3) центральной разности:
y i
y y i 1 y i 1 y i 1 y i 1
.
x x i 1 x i 1
2 h
y i
y i 1 y i 1
0(h 2 ),
2 h
10
11.
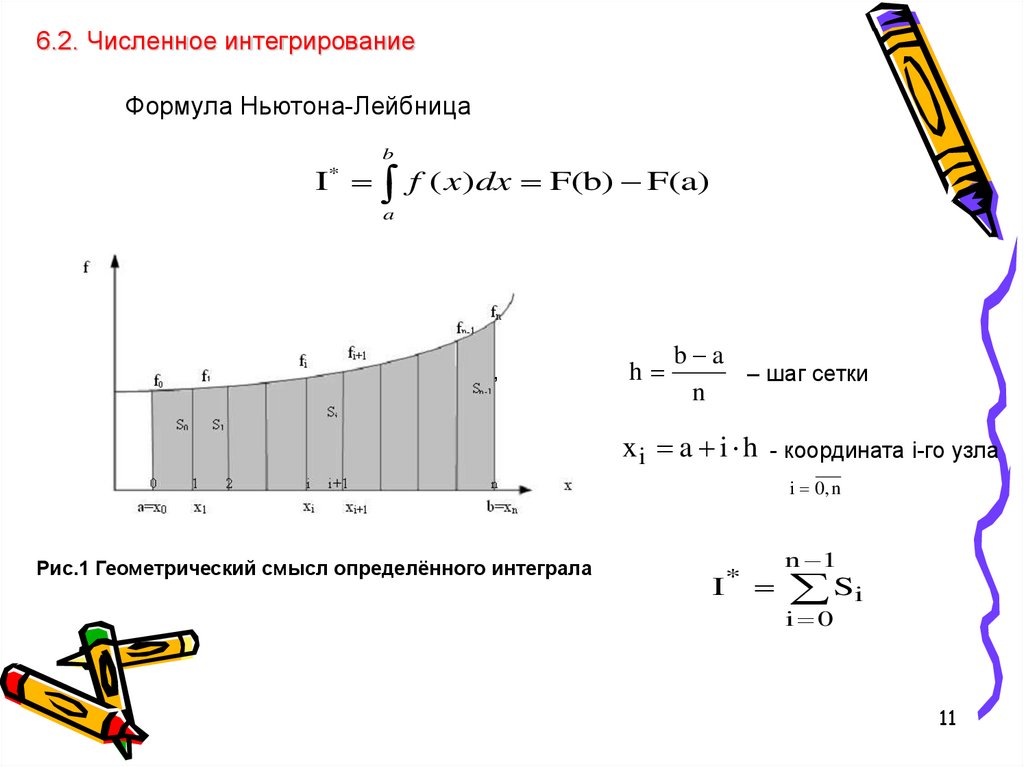
6.2. Численное интегрированиеФормула Ньютона-Лейбница
b
I f ( x)dx F(b) F(a)
*
a
,
h
b a
– шаг сетки
n
x i a i h - координата i-го узла
i 0, n
Рис.1 Геометрический смысл определённого интеграла
I
*
n 1
Si
i 0
11
12.
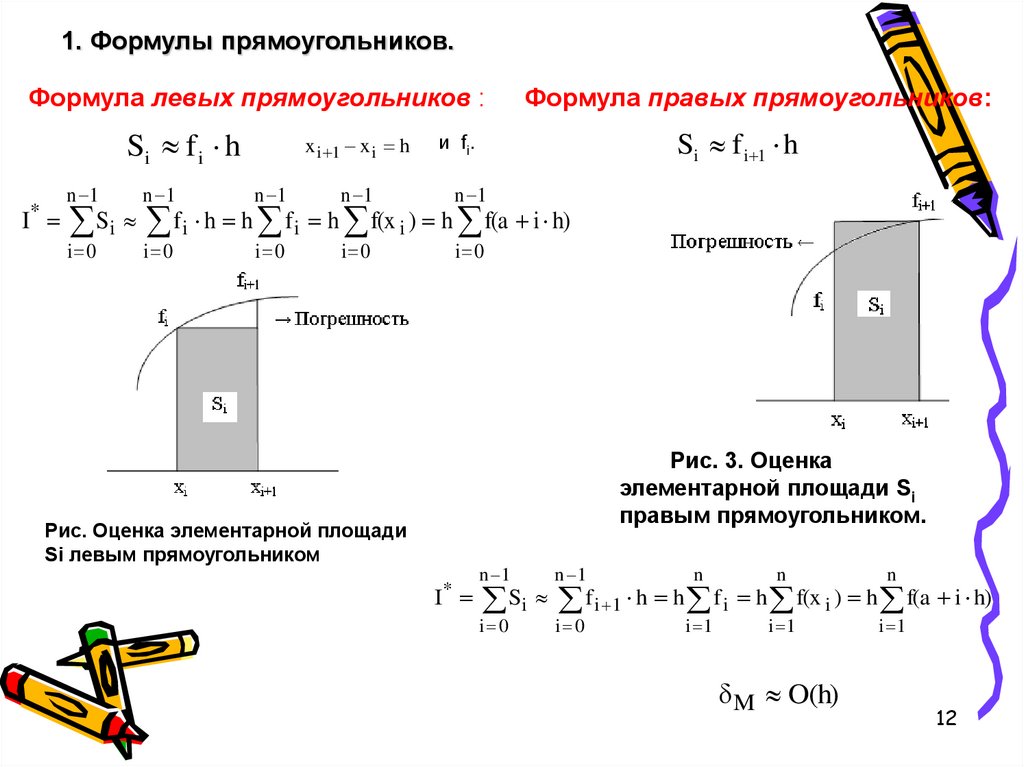
1. Формулы прямоугольников.Формула левых прямоугольников :
Si f i h
x i 1 x i h
и fi.
Формула правых прямоугольников:
Si f i 1 h
n 1
n 1
n 1
n 1
n 1
i 0
i 0
i 0
i 0
i 0
I Si f i h h f i h f(x i ) h f(a i h)
*
Рис. 3. Оценка
элементарной площади Si
правым прямоугольником.
Рис. Оценка элементарной площади
Si левым прямоугольником
n 1
n 1
n
n
n
i 0
i 0
i 1
i 1
i 1
I Si f i 1 h h f i h f(x i ) h f(a i h)
*
δ M O(h)
12
13.
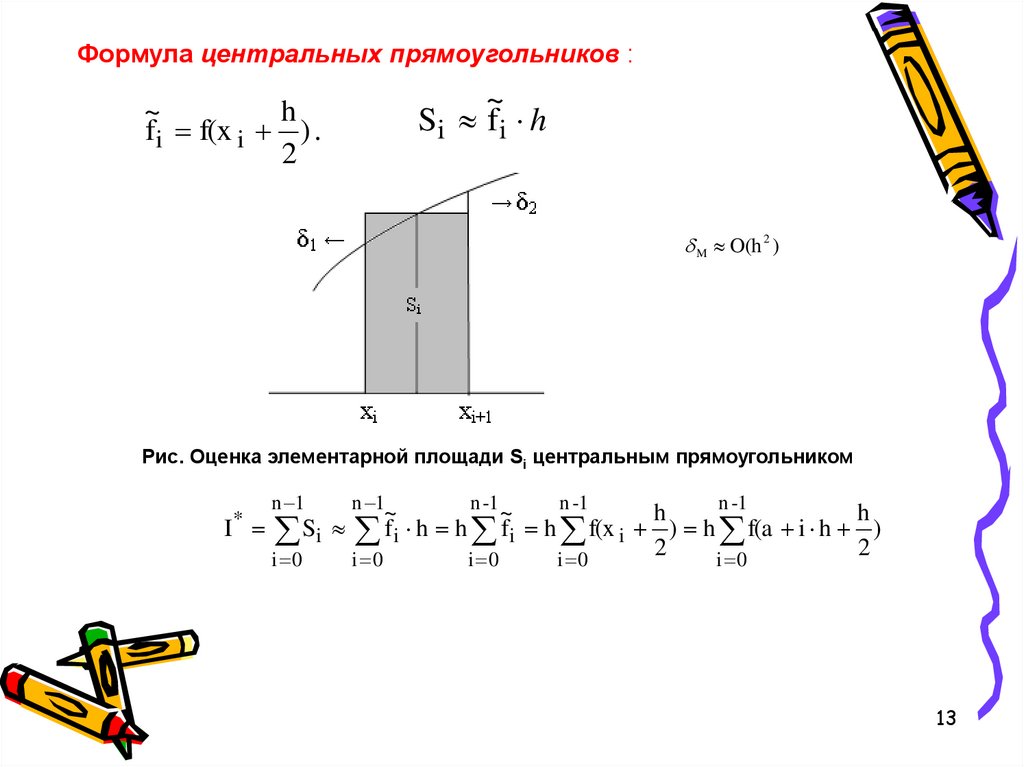
Формула центральных прямоугольников :~
Si fi h
~
h
fi f(x i ) .
2
M O(h 2 )
Рис. Оценка элементарной площади Si центральным прямоугольником
n 1
n 1
n -1
n -1
n -1
~
~
h
h
I Si fi h h fi h f(x i ) h f(a i h )
2
2
i 0
i 0
i 0
i 0
i 0
*
13
14.
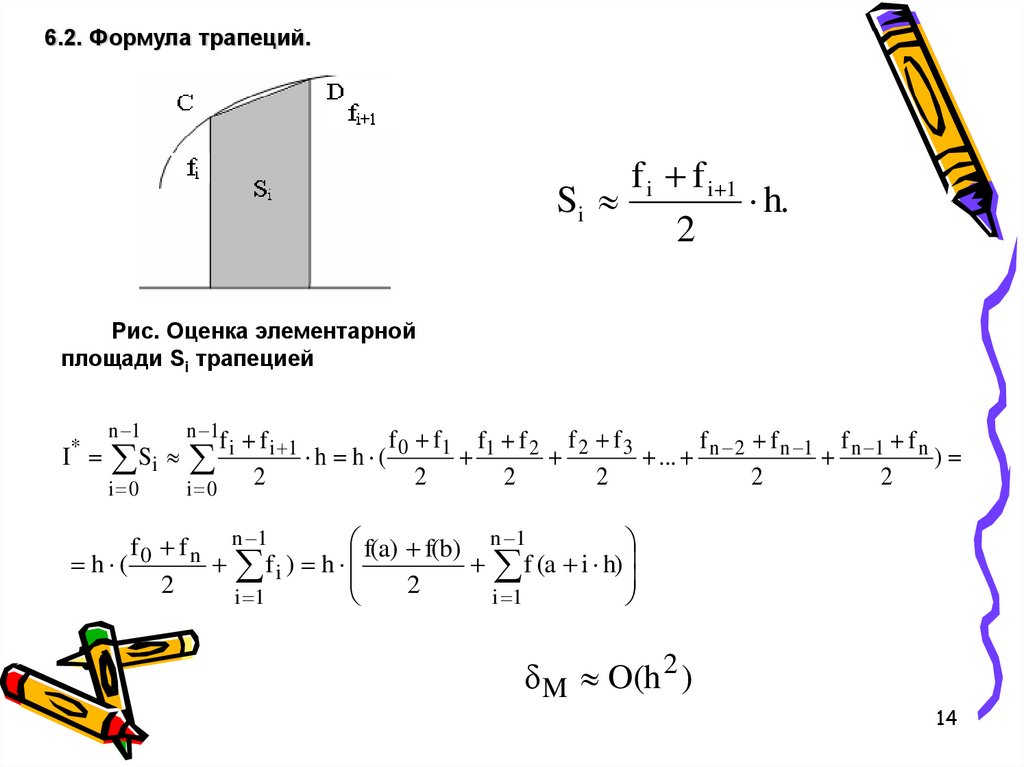
6.2. Формула трапеций.f i f i 1
Si
h.
2
Рис. Оценка элементарной
площади Si трапецией
n 1
n 1
f f f f
f f
f f
f
f
f
f
I Si i i 1 h h ( 0 1 1 2 2 3 ... n 2 n 1 n 1 n )
2
2
2
2
2
2
i 0
i 0
*
f(a) f(b) n 1
f 0 f n n 1
h (
fi ) h
f (a i h)
2
2
i 1
i 1
δ M O(h 2 )
14
15.
6.3. Формула Симпсона(x i , fi )
(x i 1 , fi 1 )
(x i
h ~
, fi )
2
~
h
h
h
Si f i 4 fi f i 1 f(x i ) 4f(x i ) f(x i 1 )
6
6
2
n 1
~
h
f i 4 fi f i 1
i 0 6
~
~
~
~
h
f 0 4 f0 f1 f1 4 f1 f 2 ... f n 2 4 fn 2 f n 1 f n 1 4 fn 1 f n
6
I
*
~
h f n f 0 n 1
I
f i 2 fi
3 2
i 0
*
h f(b) f(a) n 1
h
f(a ih) 2f(a ih )
3
2
2
i 0
м = О(h3)
15
16.
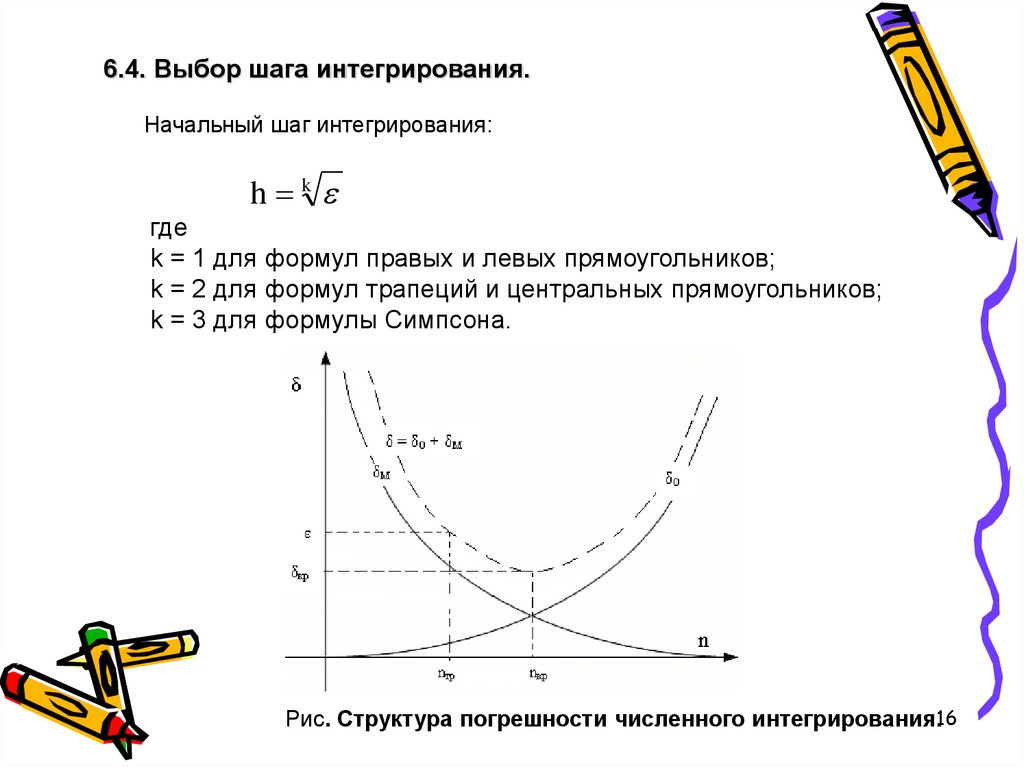
6.4. Выбор шага интегрирования.Начальный шаг интегрирования:
h k
где
k = 1 для формул правых и левых прямоугольников;
k = 2 для формул трапеций и центральных прямоугольников;
k = 3 для формулы Симпсона.
Рис. Структура погрешности численного интегрирования.16







 mathematics
mathematics








