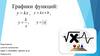Графики функций у = kx, y=kx + b, y=k/x, y=x, y=x, y=[x] и их свойства

1.

2.

Числовой функцией называется
соответствие (зависимость), при котором
каждому значению одной переменной
сопоставляется по некоторому правилу
единственное значение другой
переменной.
Обозначают латинскими (иногда
греческими) буквами: f, q, h, y, p и т.д.

3.

Определение функции
Функцией называют такую зависимость
переменной y от переменной х, при которой
каждому значению переменной х
соответствует единственное значение
переменной у
• х - независимая переменная или аргумент
функции,
• у - зависимая переменная или значение
функции

4.

Если зависимость переменной у от переменной х
является функцией, то коротко , то записывают
так: y=f(x).
Функция задана формулой
Ее можно записать:
Найти значение функции f для значений x,
равных 2,5 и -3

5.

• Область определения D(y)
• Область значений E(y)
• Нули функции y=0
• Четность
• Промежутки знакопостоянства y>0, y<0
• Непрерывность
• Монотонность (возрастание, убывание)
• Наибольшее и наименьшее значения yнаиб., yнаим.
• Ограниченность
• Выпуклость

6.

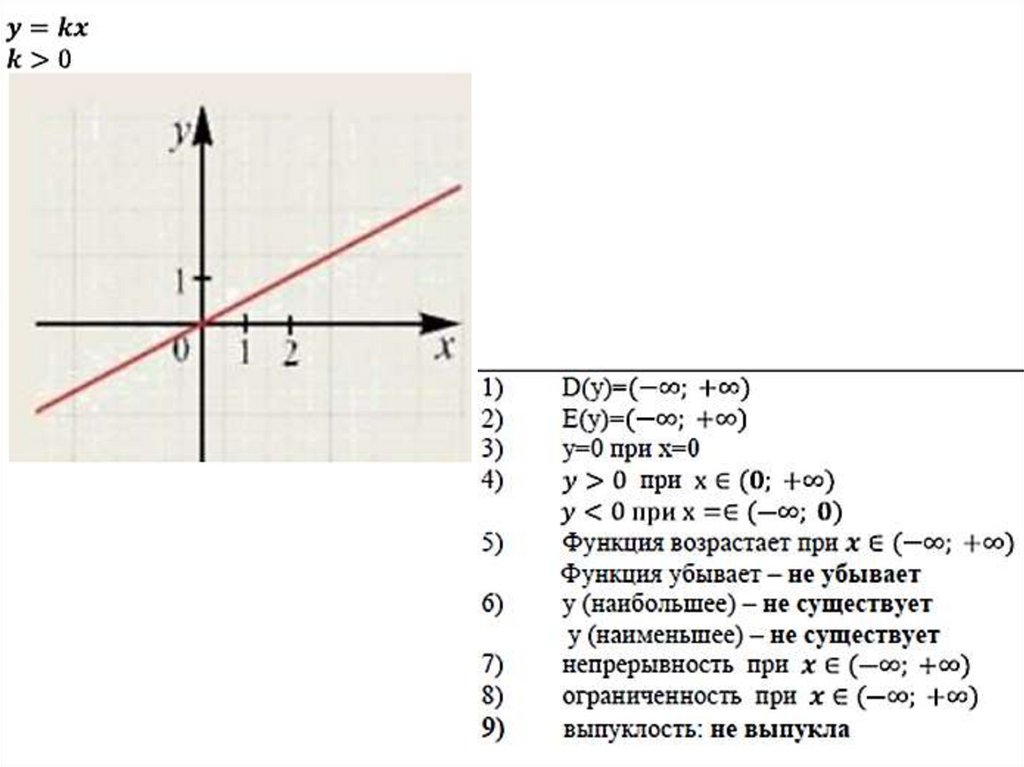
7.

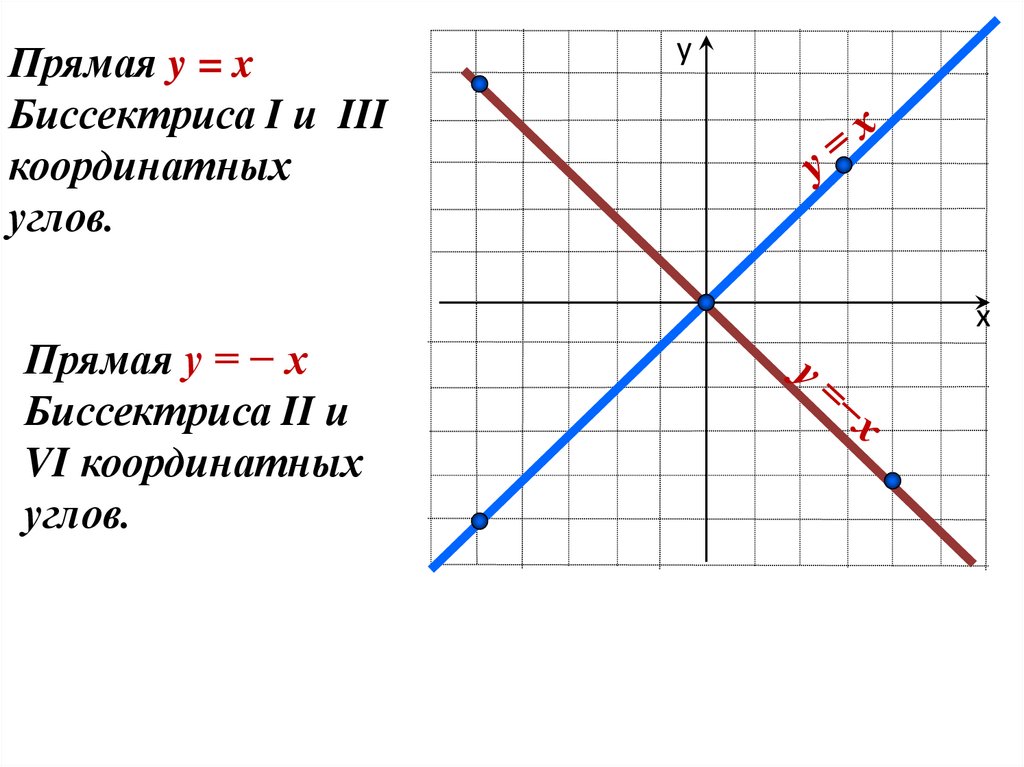
При х = 0 величина у = k · 0 при любом
значении k.
Следовательно график проходит через точку
(0; 0) – начало координат
Поэтому для построения графика у = k х
достаточно взять еще только одну точку.

8.

Пример 1
y
Построить график функции
а) у = -2,5х
1. Прямая пропорциональная
зависимость, ее график
проходит через начало
координат (0; 0).
2. Получим еще одну точку: (2; -5)
3. Построим через эту точку
и начало координат (0; 0)
прямую, которая будет
графиком функции.
O
1 2
-5
(2; -5)
x

9.

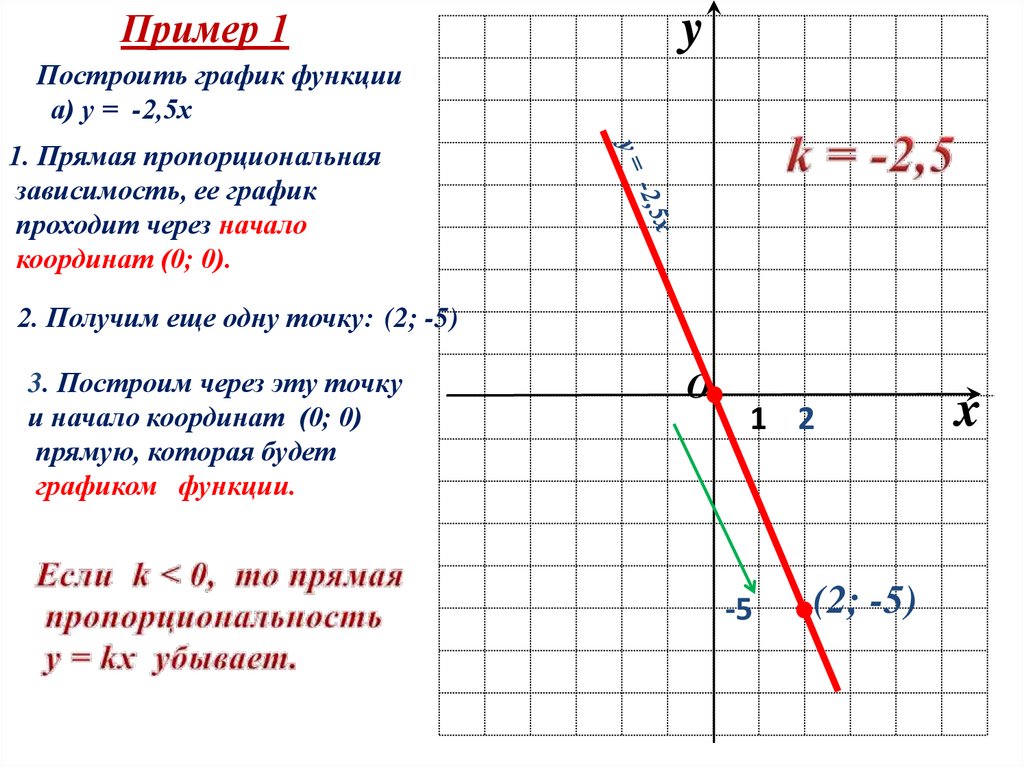
Прямая y = x
Биссектриса I и III
координатных
углов.
у
х
Прямая y = − x
Биссектриса II и
VI координатных
углов.

10.

11.

12.

13.

Линейной функцией называется функция,
которую можно задать формулой вида
k, b – некоторые числа.

14.

15.

16.

Пример 1
y
Построить график функции
у = 2х + 3, найти точку
пересечения с осью оу.
(1; 5)
5
1. Составим таблицу значений:
х
у
0
3
3 (0; 3)
1
5
2. Получим точки: (0; 3), (1; 5)
3. Построим эти точки и
через них проведем прямую.
Точка пересечения с осью оу:
(0; 3) т. е. при т = 3
O
1
x

17.

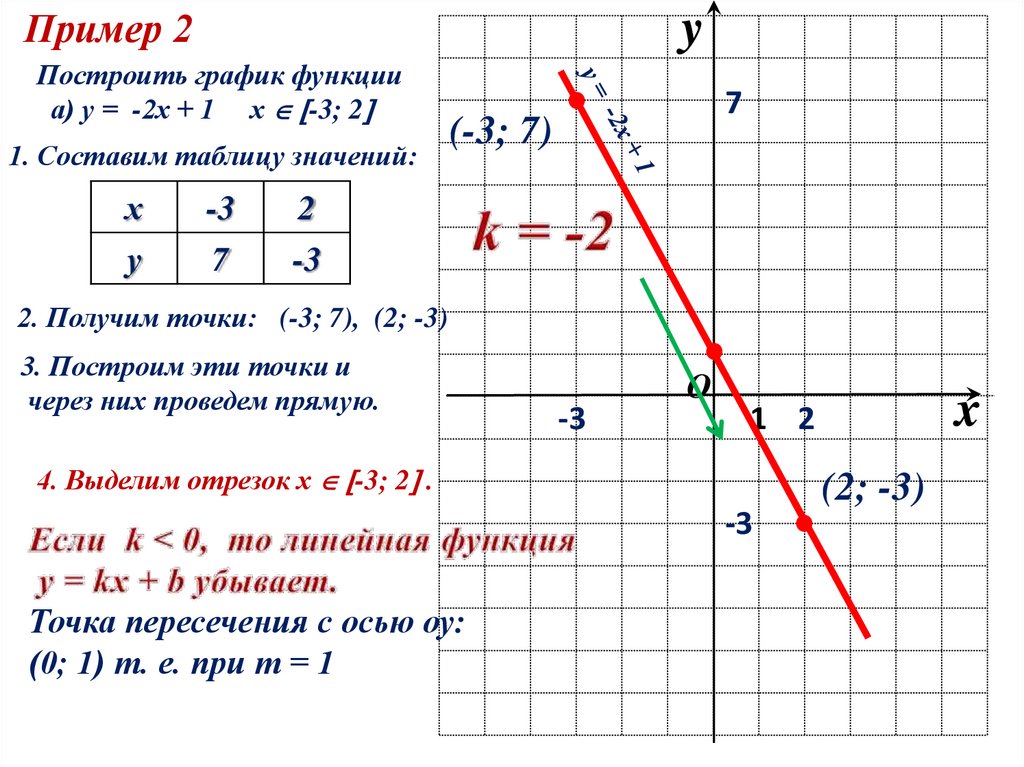
Пример 2
y
Построить график функции
а) у = -2х + 1 х -3; 2
1. Составим таблицу значений:
х
-3
2
у
7
-3
7
(-3; 7)
2. Получим точки: (-3; 7), (2; -3)
3. Построим эти точки и
через них проведем прямую.
-3
O
4. Выделим отрезок х -3; 2 .
(2; -3)
-3
Точка пересечения с осью оу:
(0; 1) т. е. при т = 1
x
1 2

18.

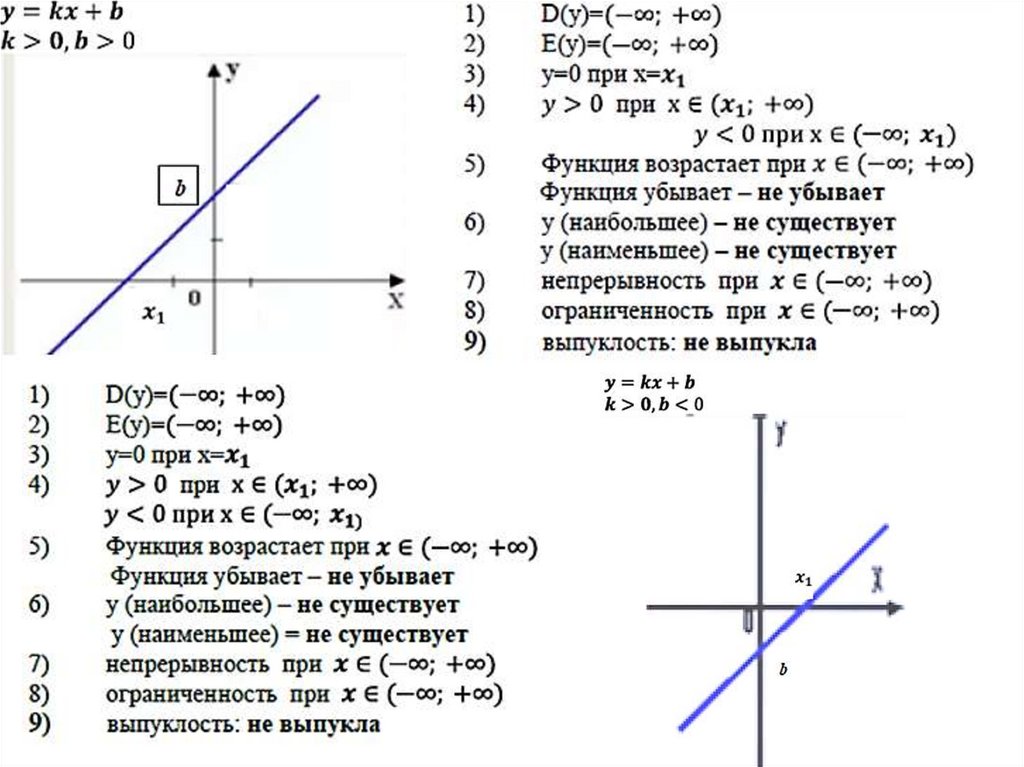
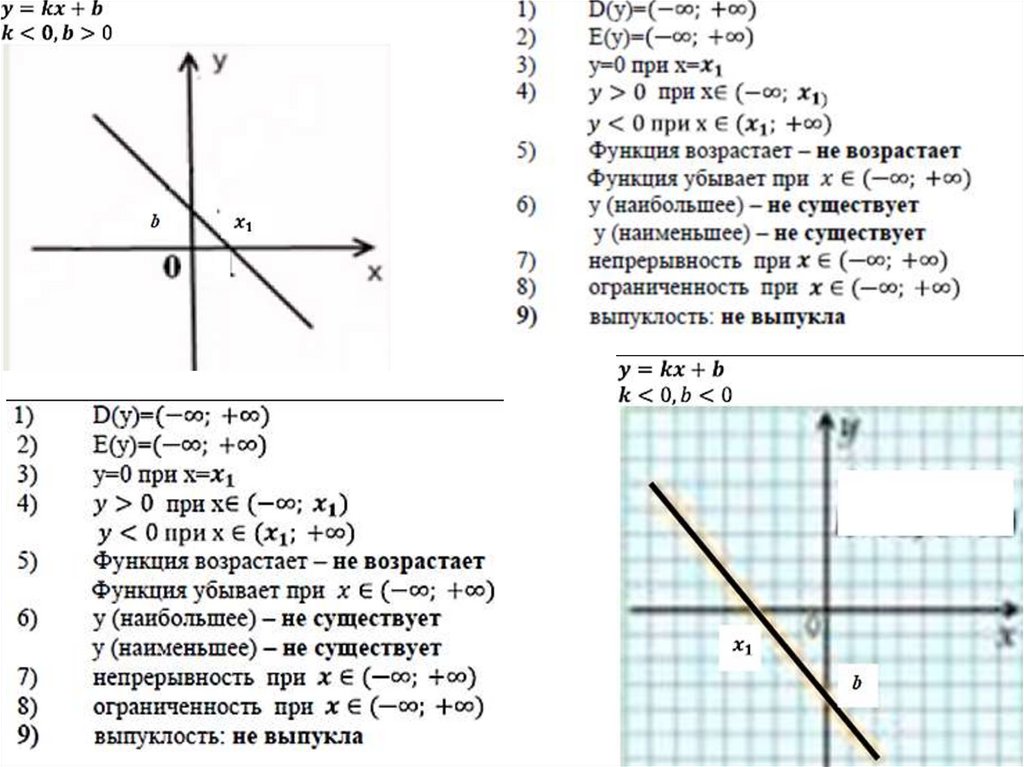
Величина k определяет наклон графика
функции y = kx + b

19.

20.

21.

Обратной пропорциональностью
называется функция, которую
можно задавать формулой вида
где х – независимая переменная,
k – не равное нулю число.

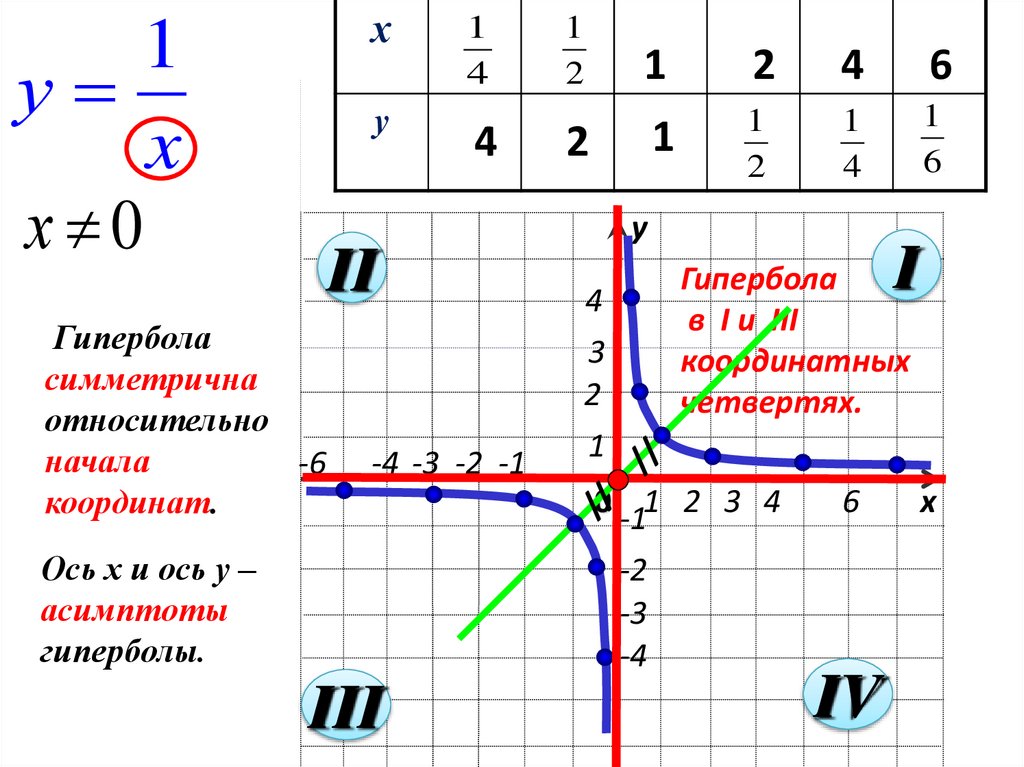
22.

х
1
у
x
х 0
у
1
4
4
1
2
1
2
4
6
1
1
2
1
4
1
6
2
у
II
Гипербола
симметрична
относительно
начала
-6
координат.
-4 -3 -2 -1
Ось х и ось у –
асимптоты
гиперболы.
4
3
2
1
0 -11 2 3 4
-2
-3
-4
III
I
Гипербола
в I и III
координатных
четвертях.
6
IV
х

23.

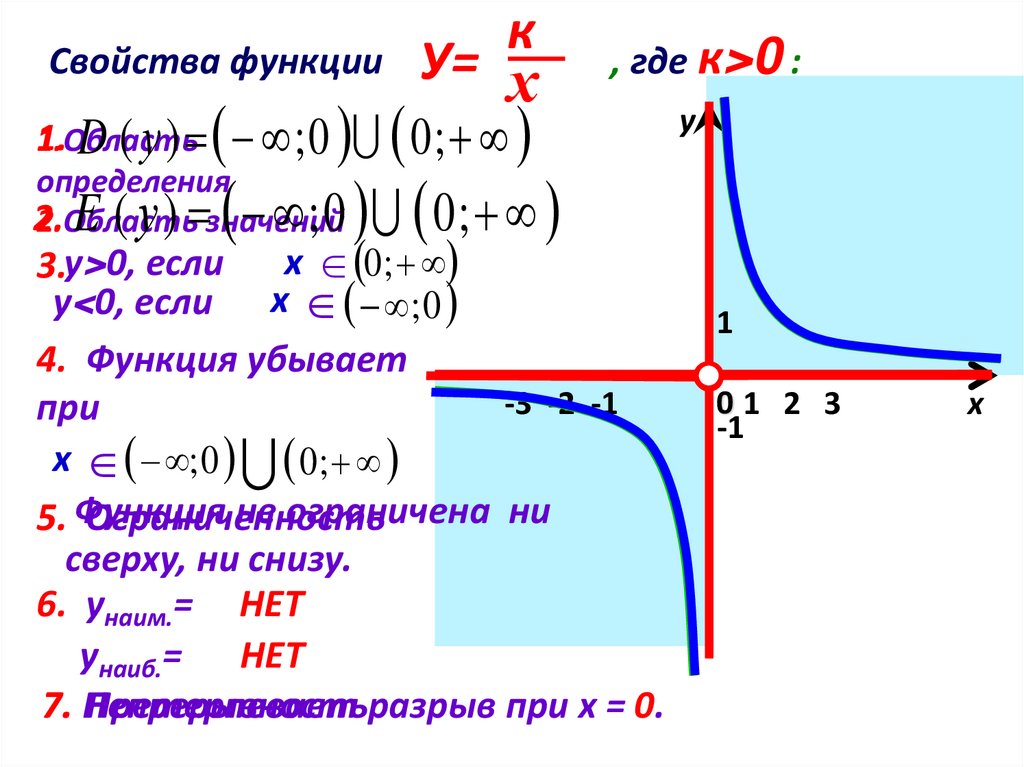
Свойства функции
к
У= х
0;
1.
1.Область
D ( у ) ;0
, где к>0 :
E ( у ) ; 0 0;
х 0 ;
3.у>0, если
у<0, если х ; 0
у
определения
2.
2.Область значений
4. Функция убывает
-3 -2 -1
при
х ; 0 0 ;
не ограничена ни
5. Функция
Ограниченность
сверху, ни снизу.
6. унаим.= НЕТ
унаиб.= НЕТ
7. Непрерывность
Претерпевает разрыв при х = 0.
1
01 2 3
-1
х

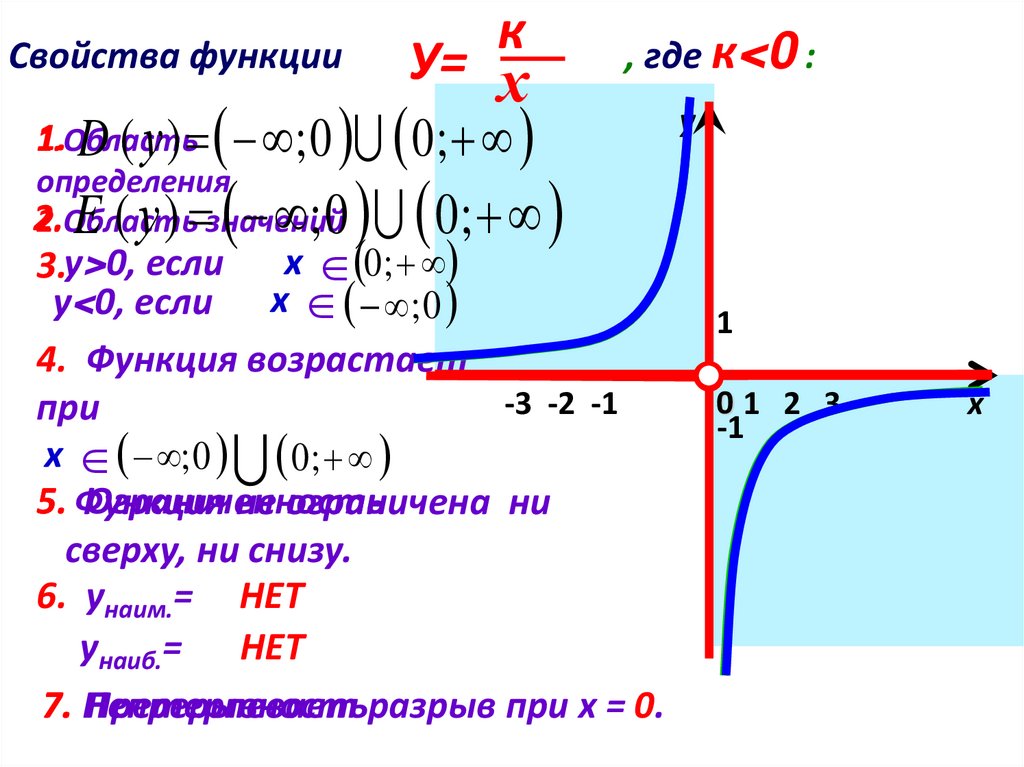
24.

к
У= х
1.
1.Область
D ( у ) ; 0 0 ;
определения
2.
2.Область
; 0 0;
E ( у ) значений
Свойства функции
, где к<0 :
х 0 ;
3.у>0, если
у<0, если х ; 0
4. Функция возрастает
-3 -2 -1
при
х ; 0 0 ;
5. Функция
Ограниченность
не ограничена ни
сверху, ни снизу.
6. унаим.= НЕТ
унаиб.= НЕТ
7. Непрерывность
Претерпевает разрыв при х = 0.
у
1
01 2 3
-1
х

25.

х
у
0
1
2
0
1
8
у
0
1
х
Кубическая парабола

26.

Свойства функции у = х3
1) D(f) = (– ∞; + ∞);
2) Е(f) = (– ∞; + ∞);
3) нечетная функция;
4) возрастает;
5) не ограничена ни снизу, ни сверху;
6) нет ни наименьшего, ни наибольшего
значений;
7) непрерывна;
8) выпукла вверх при х < 0, выпукла вниз
при х > 0.

27.

График функции
x 0
у х

28.

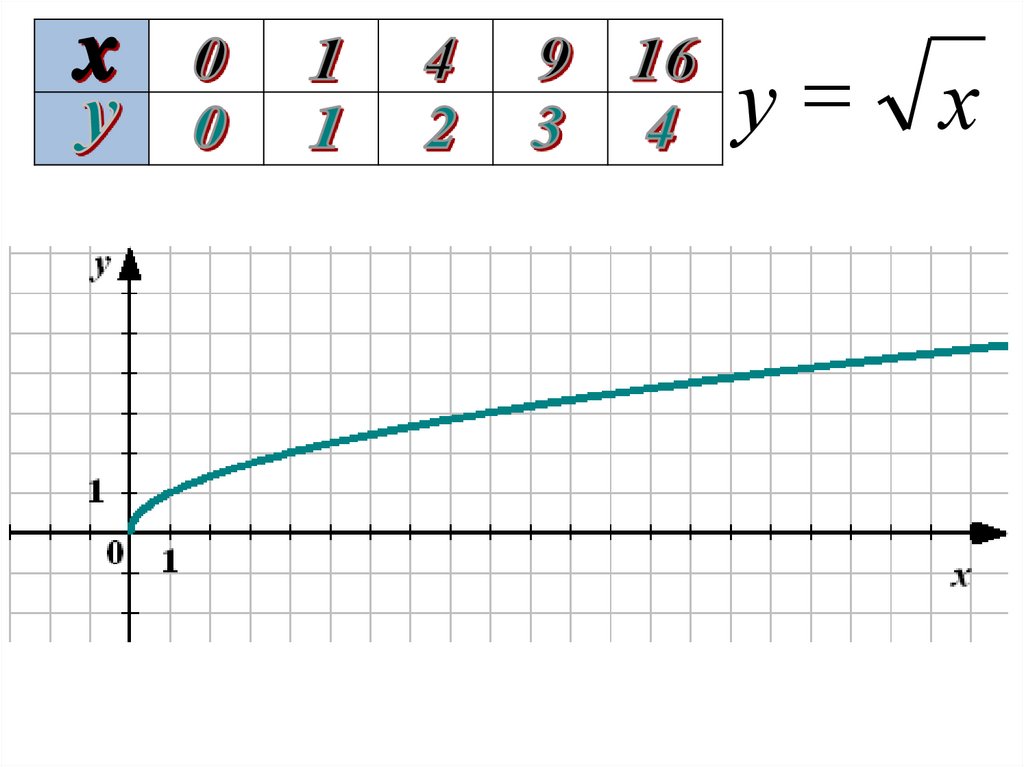
у х
4
3
2
4
9
16

29.

Свойства функции
у х

30.

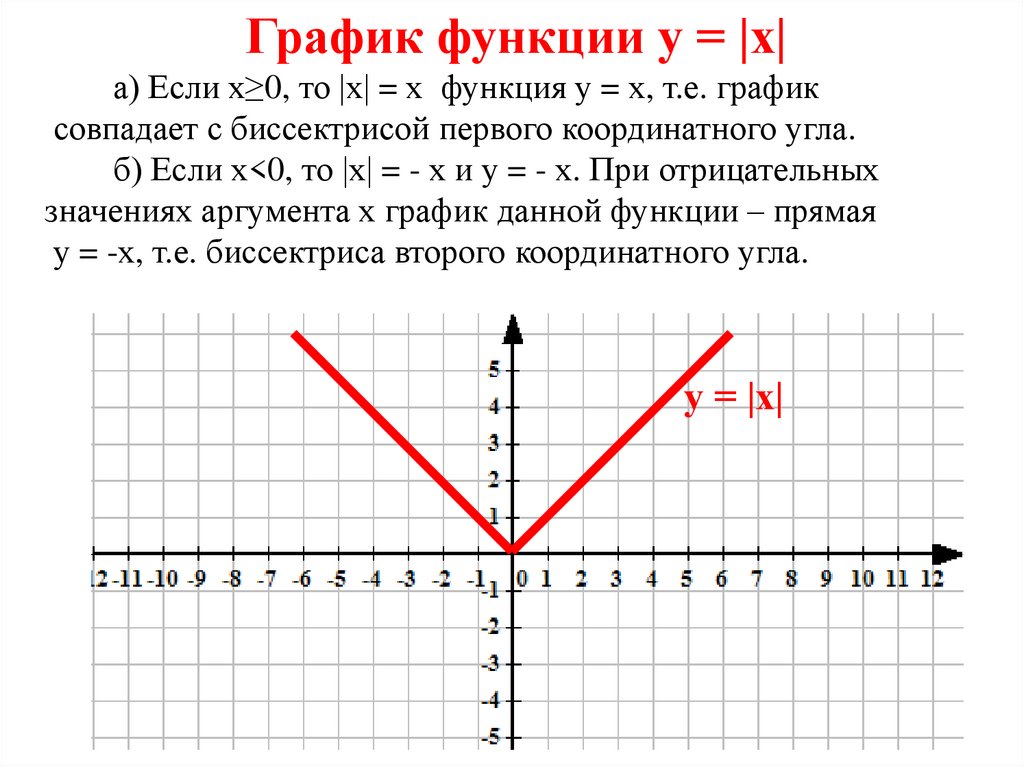
График функции у = |х|
а) Если х≥0, то |х| = х функция у = х, т.е. график
совпадает с биссектрисой первого координатного угла.
б) Если х<0, то |х| = - х и у = - х. При отрицательных
значениях аргумента х график данной функции – прямая
у = -х, т.е. биссектриса второго координатного угла.
у = |х|

31.

Свойства функции у = |х|

32.

33.

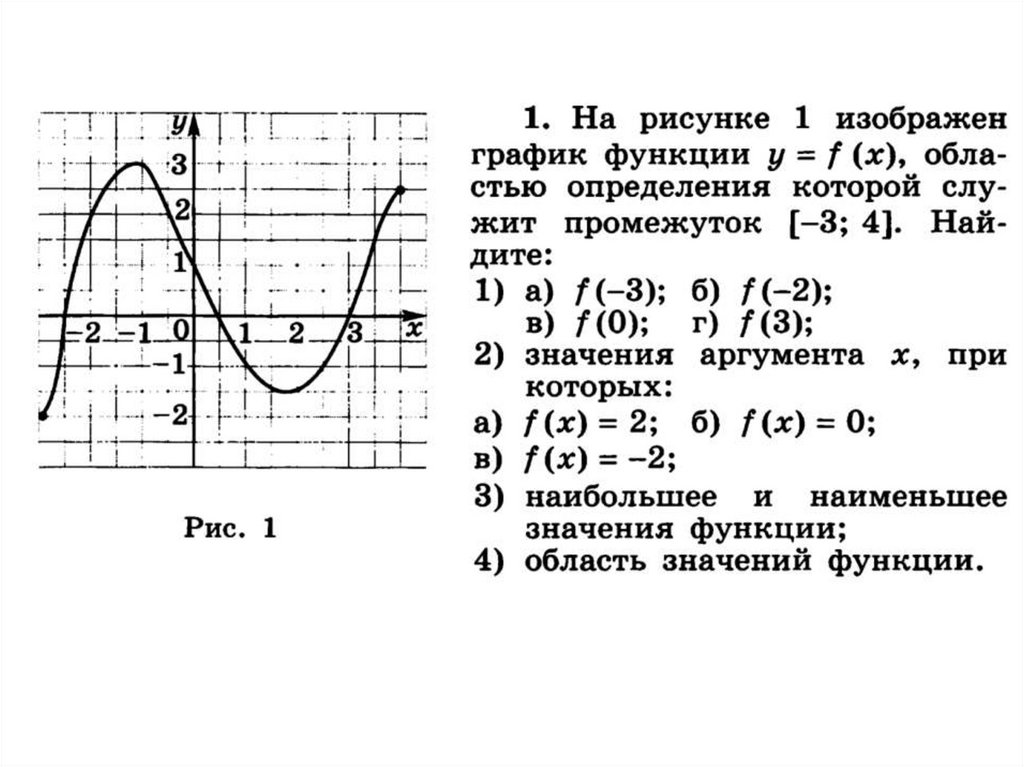
Постройте график функции и перечислите его
свойства