Графики функций y = kx, y = kx + b, y=kx, y=x³, y=√x, y=|x|. Урок № 66

1.

21.02.2025
Урок № 66
Графики функций
y = kx, y = kx + b,
y=kx, y=x³, y=√x, y=|x|

2.

Графики функций
у
х и у = |х|

3.

у
у х
3
2
1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 х

4.

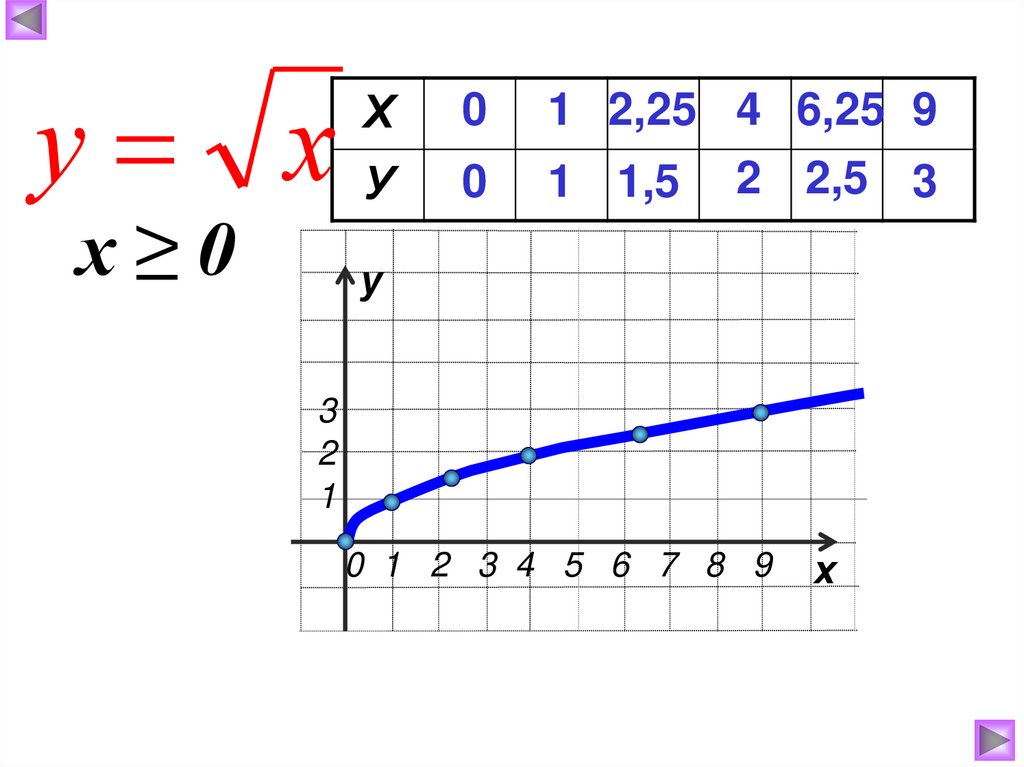
у х
х≥0
Х
0
У
0
1 2,25 4 6,25 9
1 1,5 2 2,5 3
у
3
2
1
0 1 2 3 4 5 6 7 8 9
х

5.

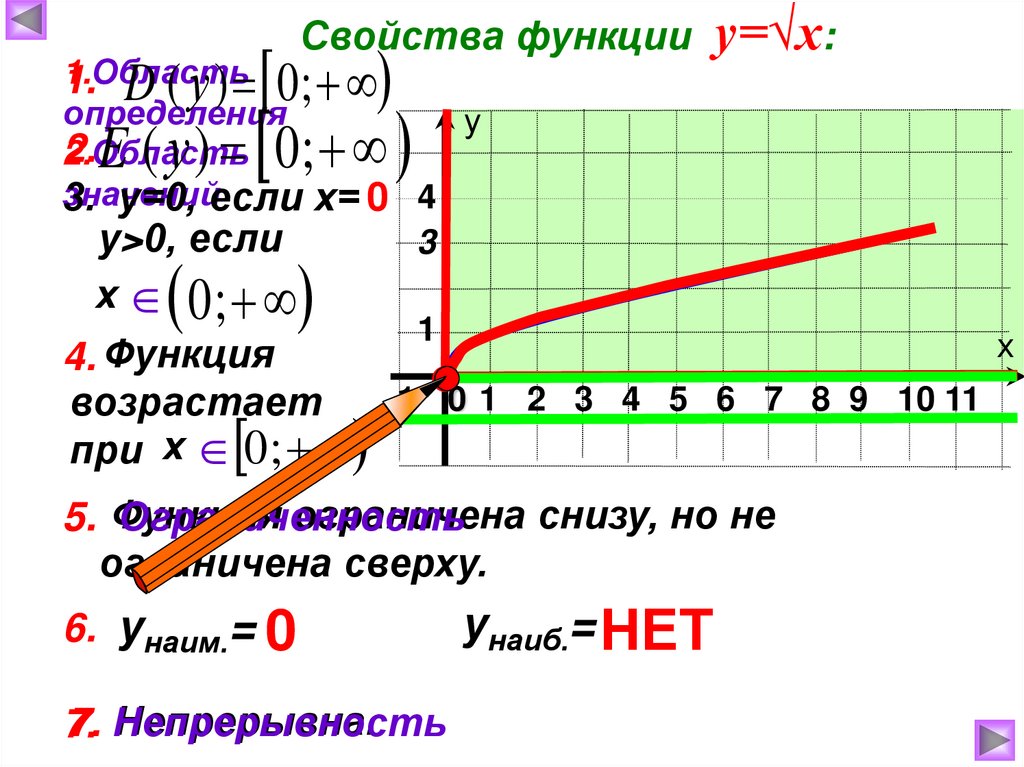
Свойства функции у=√х:
1.Область
1. D ( у ) 0 ;
определения
у
2.
2.Область
значений
3. у=0, если х= 0 4
у>0, если
3
E ( у ) 0;
х 0;
1
х
4. Функция
-1 0 1 2 3 4 5 6 7 8 9 10 11
возрастает
при х 0 ;
ограничена снизу, но не
5. Функция
Ограниченность
ограничена сверху.
6. унаим.= 0
Непрерывна.
7. Непрерывность
7.
унаиб.= НЕТ

6.

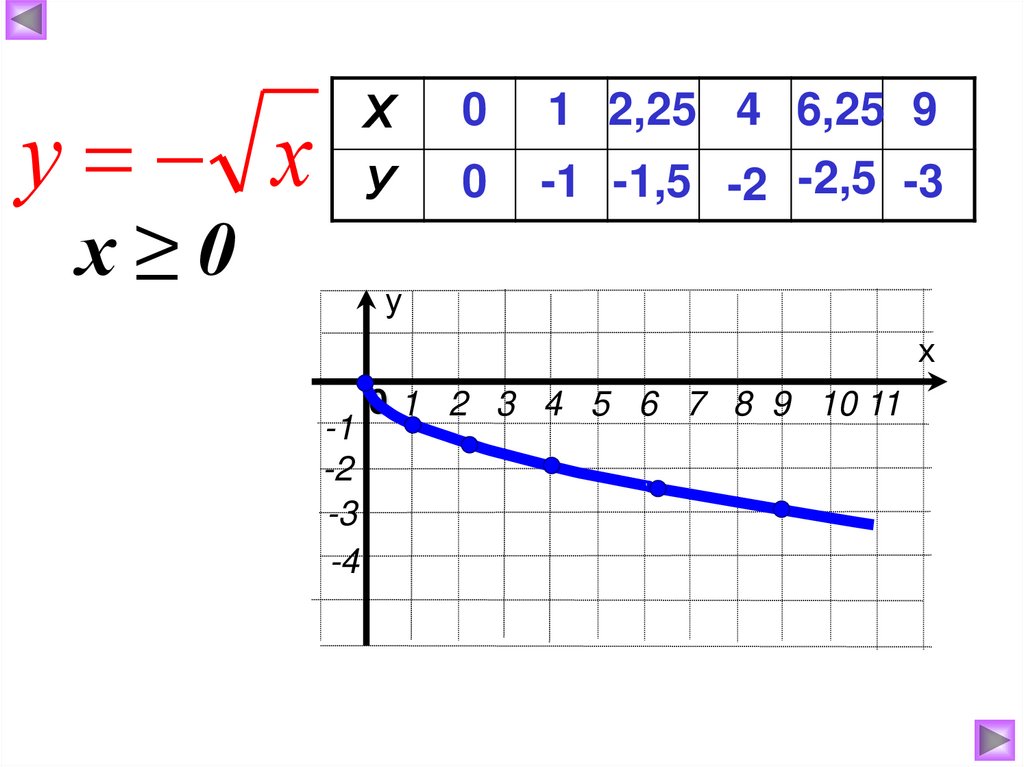
у х У 0
Х
х≥0
0
1 2,25 4 6,25 9
-1 -1,5 -2 -2,5 -3
у
х
-1
-2
-3
-4
0 1 2 3 4 5 6 7 8 9 10 11

7.

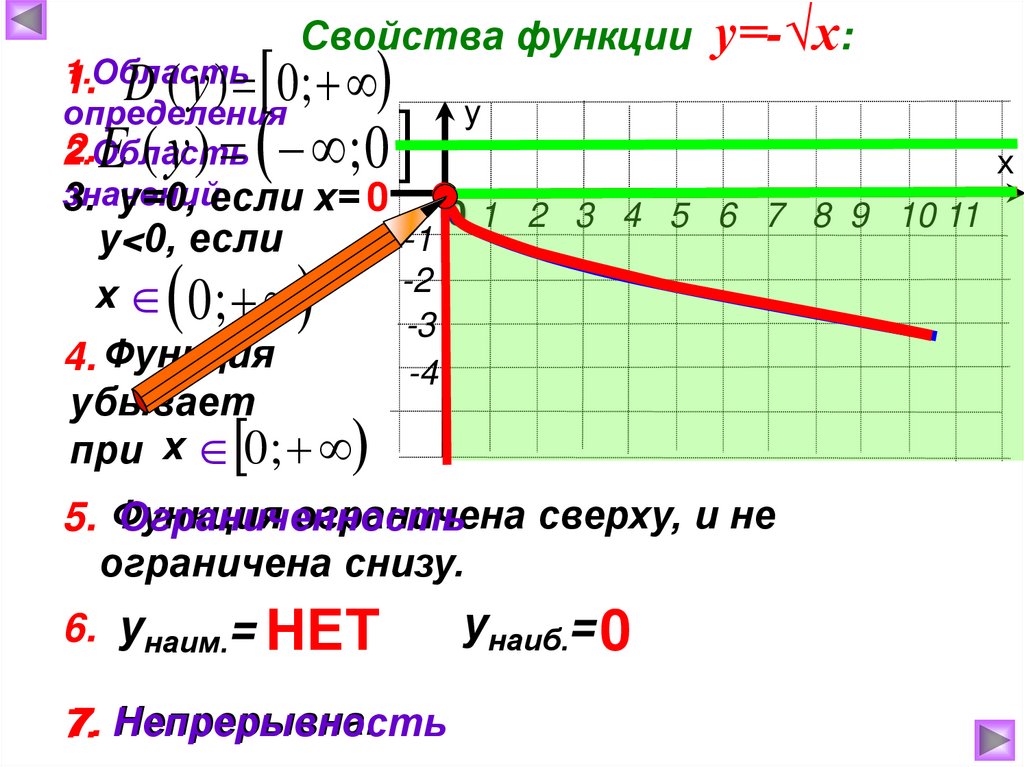
Свойства функции у=-√х:
1.Область
1. D ( у ) 0 ;
определения
2.
2.Область
значений
3. у=0, если х= 0
E ( у ) ; 0
у<0, если
х 0;
4. Функция
убывает
при х 0 ;
-1
-2
-3
-4
у
х
0 1 2 3 4 5 6 7 8 9 10 11
ограничена сверху, и не
5. Функция
Ограниченность
ограничена снизу.
6. унаим.= НЕТ
Непрерывна.
7. Непрерывность
7.
унаиб.= 0

8.

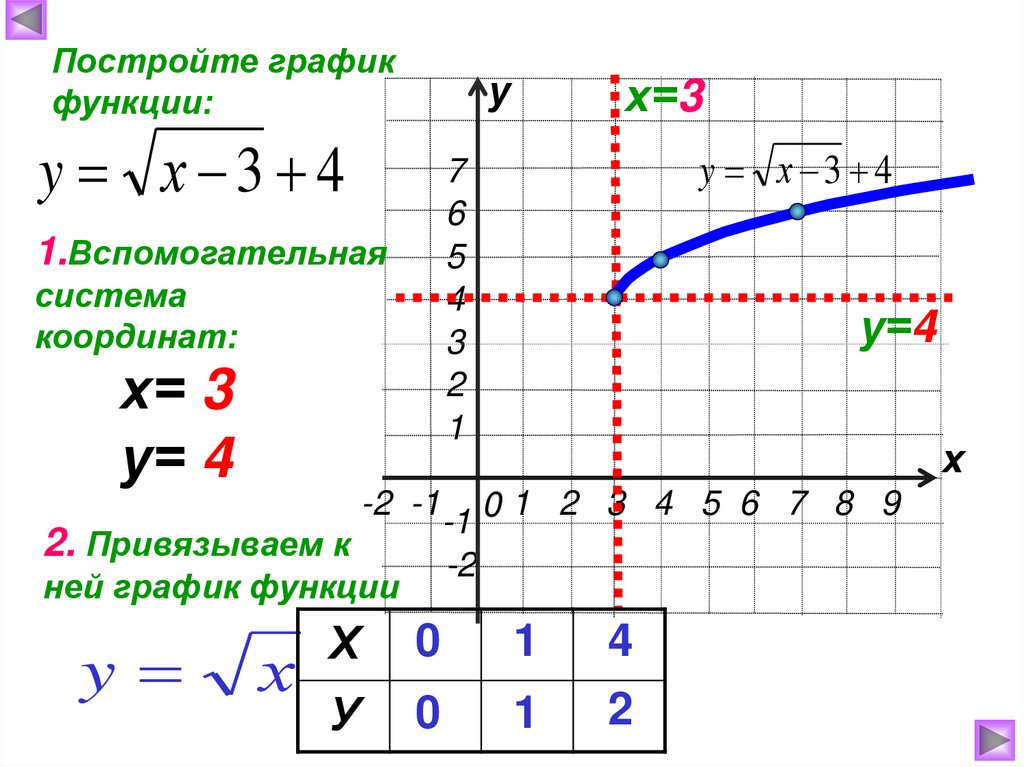
Постройте график
функции:
у
y х 3 4
система
координат:
х= 3
у= 4
-2 -1
2. Привязываем к
ней график функции
х
y х 3 4
7
6
5
4
3
2
1
1.Вспомогательная
y
х=3
-1
-2
у=4
х
01 2 3 4 5 6 7 8 9
Х
0
1
У
0
1
4
2

9.

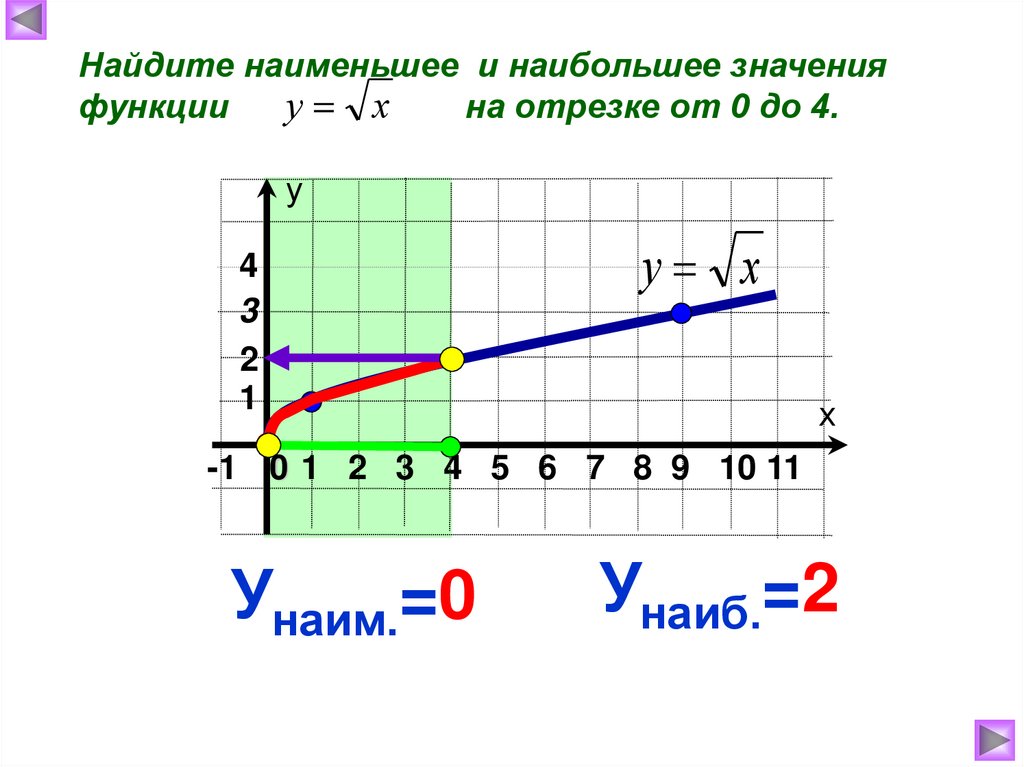
Найдите наименьшее и наибольшее значения
у х
функции
на отрезке от 0 до 4.
у
4
3
2
1
у х
х
-1 0 1 2 3 4 5 6 7 8 9 10 11
Унаим.=0
Унаиб.=2

10.

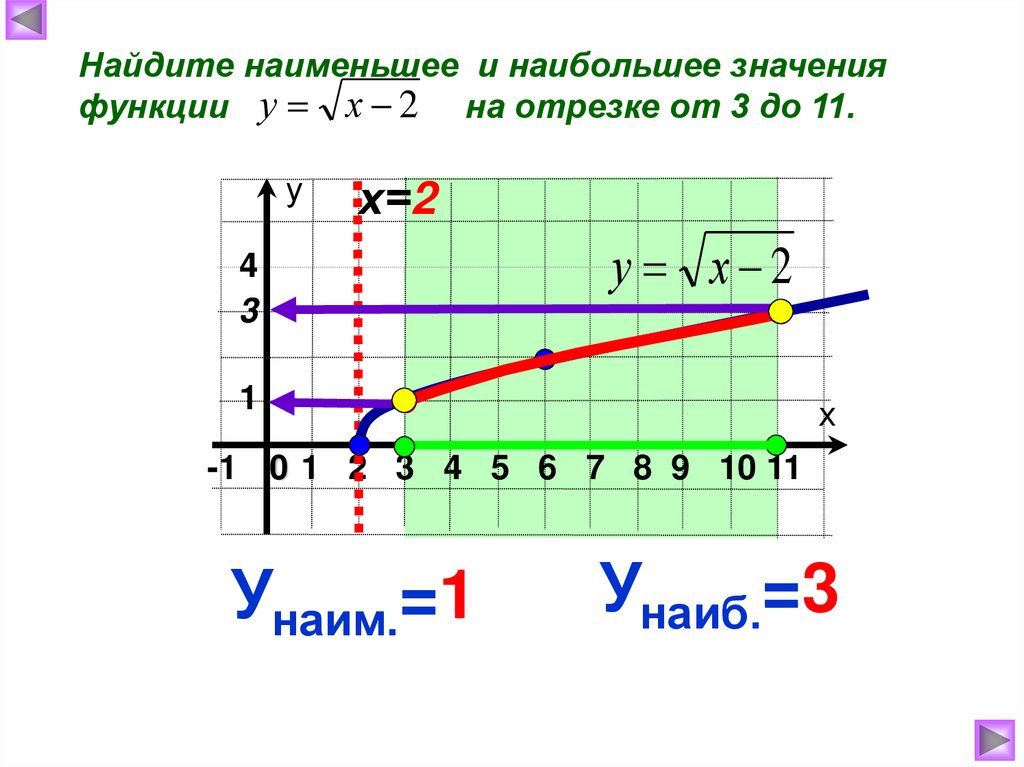
Найдите наименьшее и наибольшее значения
функции у х 2 на отрезке от 3 до 11.
у
х=2
4
3
у х 2
1
х
-1 0 1 2 3 4 5 6 7 8 9 10 11
Унаим.=1
Унаиб.=3

11.

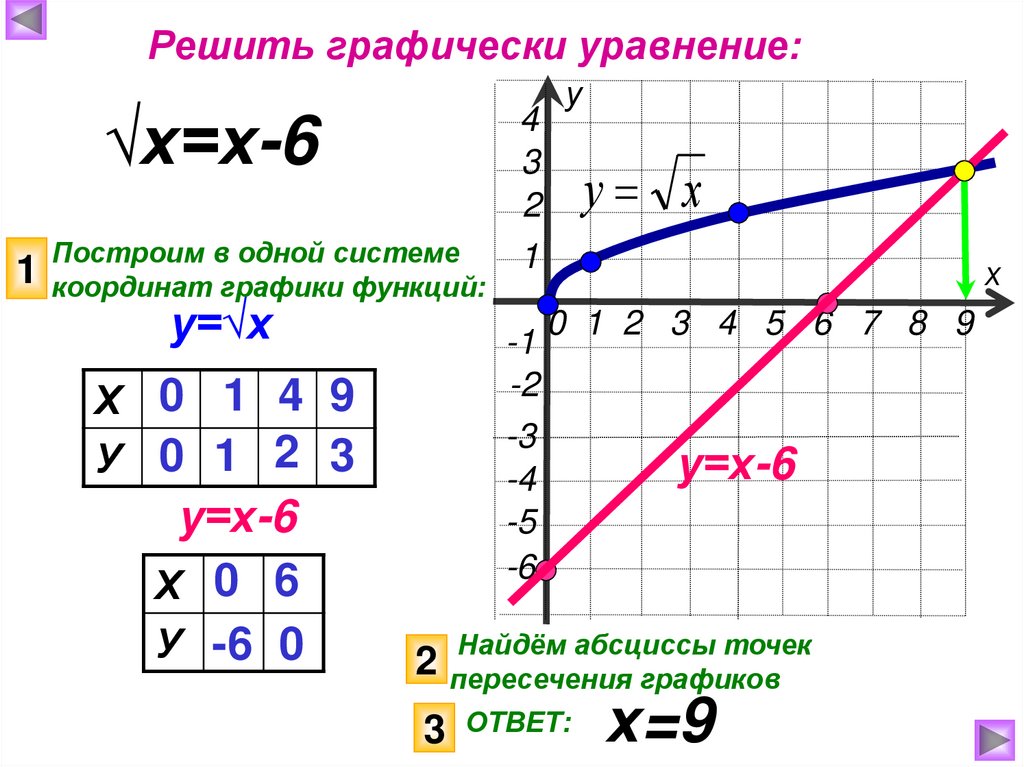
Решить графически уравнение:
√х=х-6
4
3
2
у
у х
Построим в одной системе
1 координат графики функций: 1
у=√х
Х 0 1 4 9
У 0 1 2 3
у=х-6
Х 0 6
У -6 0
-1
-2
-3
-4
-5
-6
х
0 1 2 3 4 5 6 7 8 9
у=х-6
Найдём абсциссы точек
2 пересечения графиков
3 ОТВЕТ:
х=9

12.

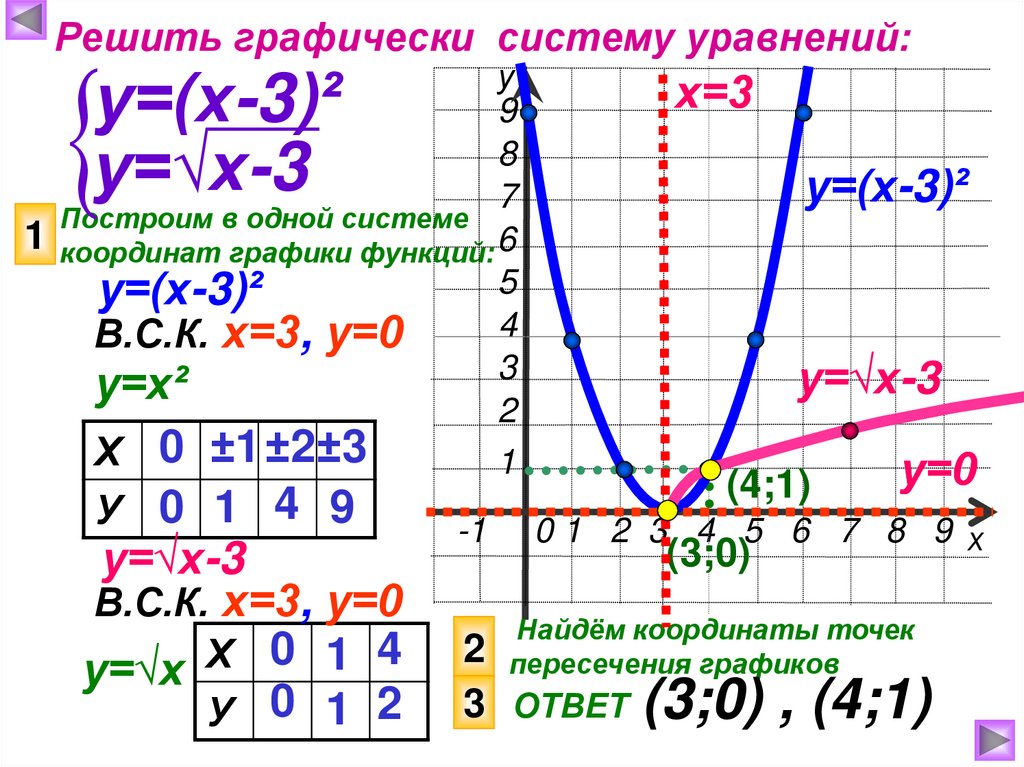
Решить графически систему уравнений:
у
9
8
7
Построим в одной системе
1 координат графики функций: 6
5
у=(х-3)²
4
В.С.К. х=3, у=0
3
у=х²
2
Х 0 ±1 ±2±3
1
у=(х-3)²
у=√х-3
У 0 1 4 9
у=√х-3
В.С.К. х=3, у=0
0
4
Х
1
у=√х
У 0 1 2
-1
х=3
у=(х-3)²
у=√х-3
(4;1)
у=0
01 2 3 4 5 6 7 8 9 х
(3;0)
Найдём координаты точек
пересечения графиков
2
3 ОТВЕТ (3;0) , (4;1)

13.

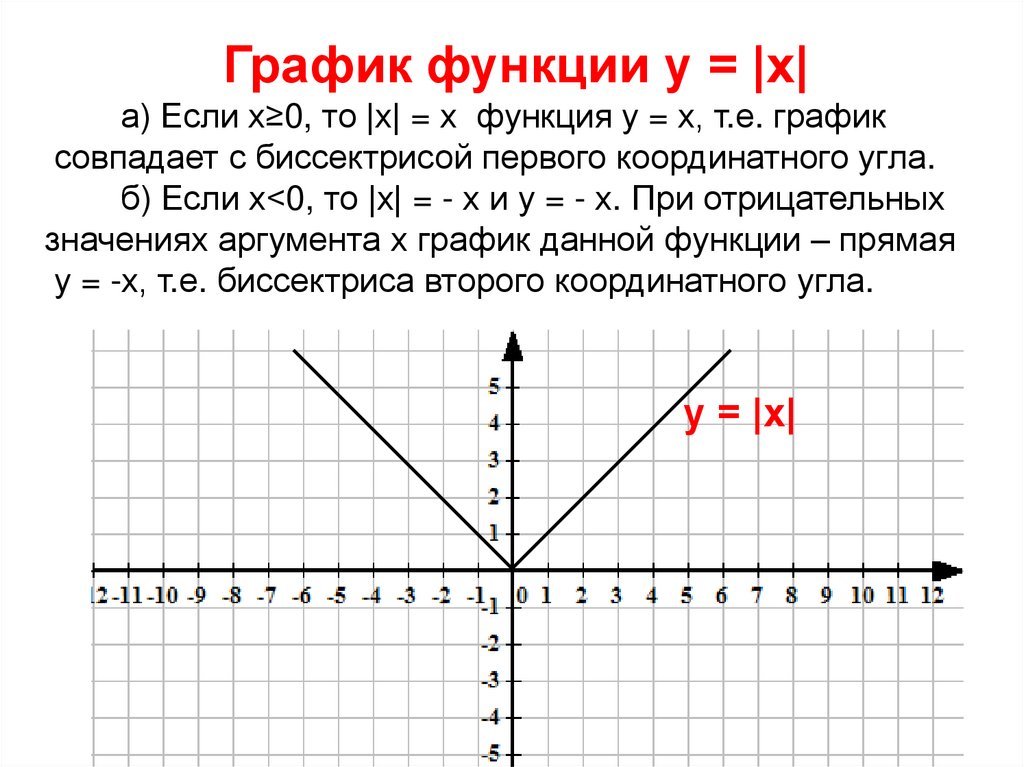
График функции у = |х|
а) Если х≥0, то |х| = х функция у = х, т.е. график
совпадает с биссектрисой первого координатного угла.
б) Если х<0, то |х| = - х и у = - х. При отрицательных
значениях аргумента х график данной функции – прямая
у = -х, т.е. биссектриса второго координатного угла.
у = |х|

14.

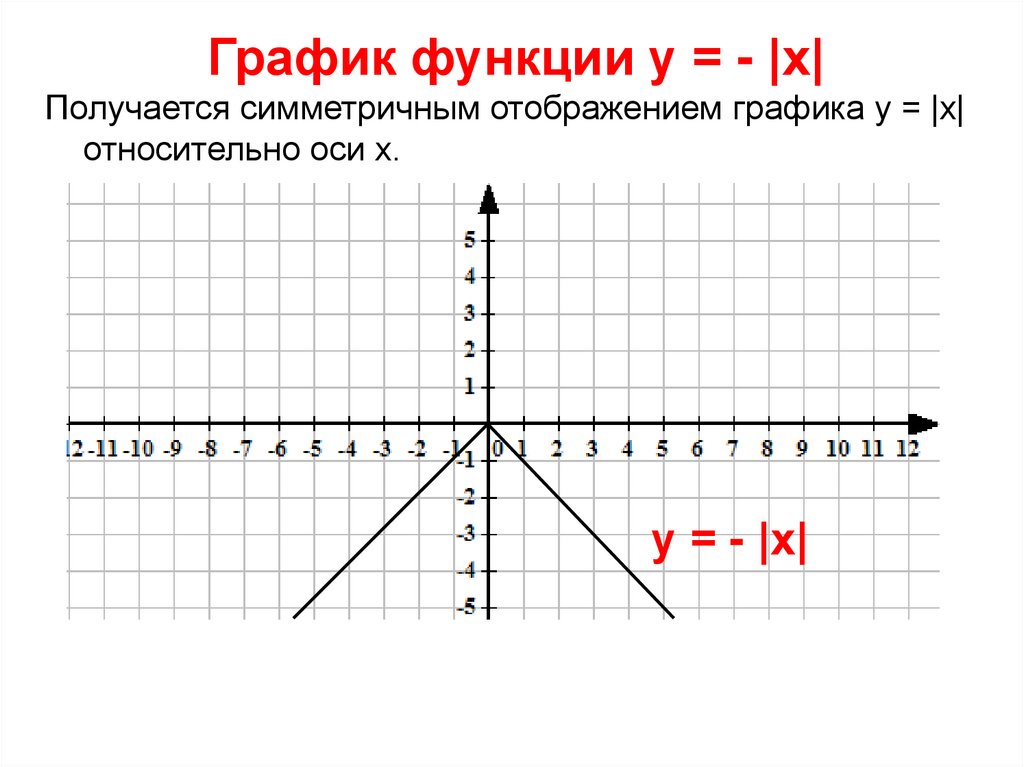
График функции у = - |х|
Получается симметричным отображением графика у = |х|
относительно оси х.
у = - |х|

15.

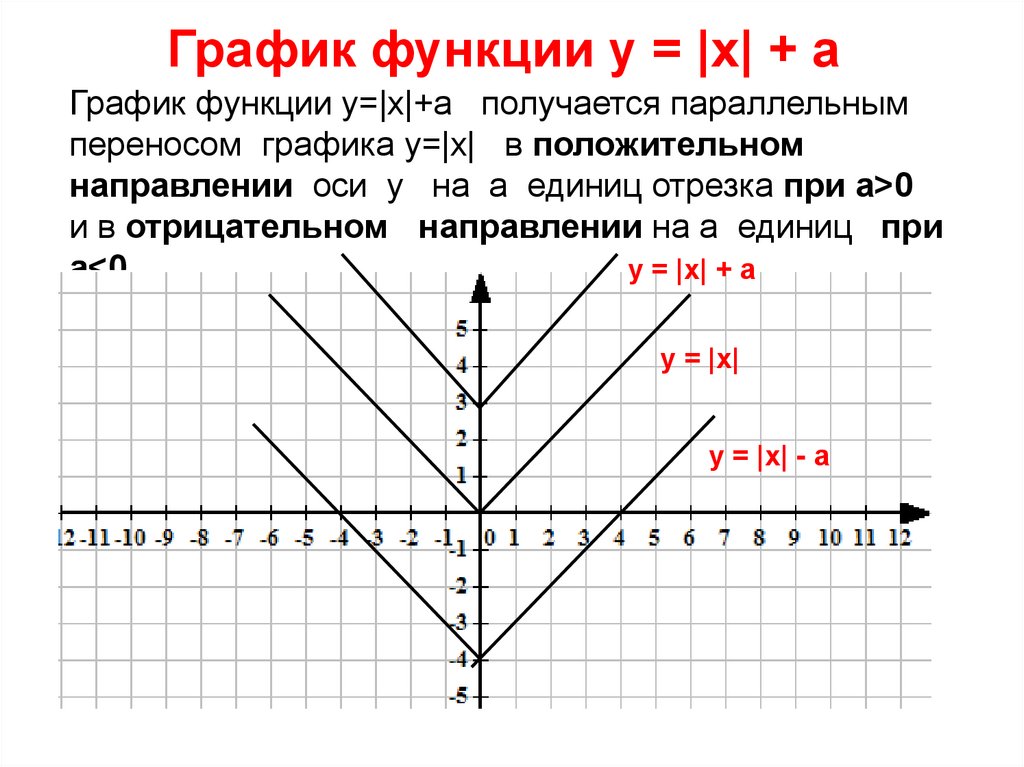
График функции у = |х| + а
График функции у=|х|+а получается параллельным
переносом графика у=|х| в положительном
направлении оси у на а единиц отрезка при а>0
и в отрицательном направлении на а единиц при
у = |х| + а
а<0.
у = |х|
у = |х| - а

16.

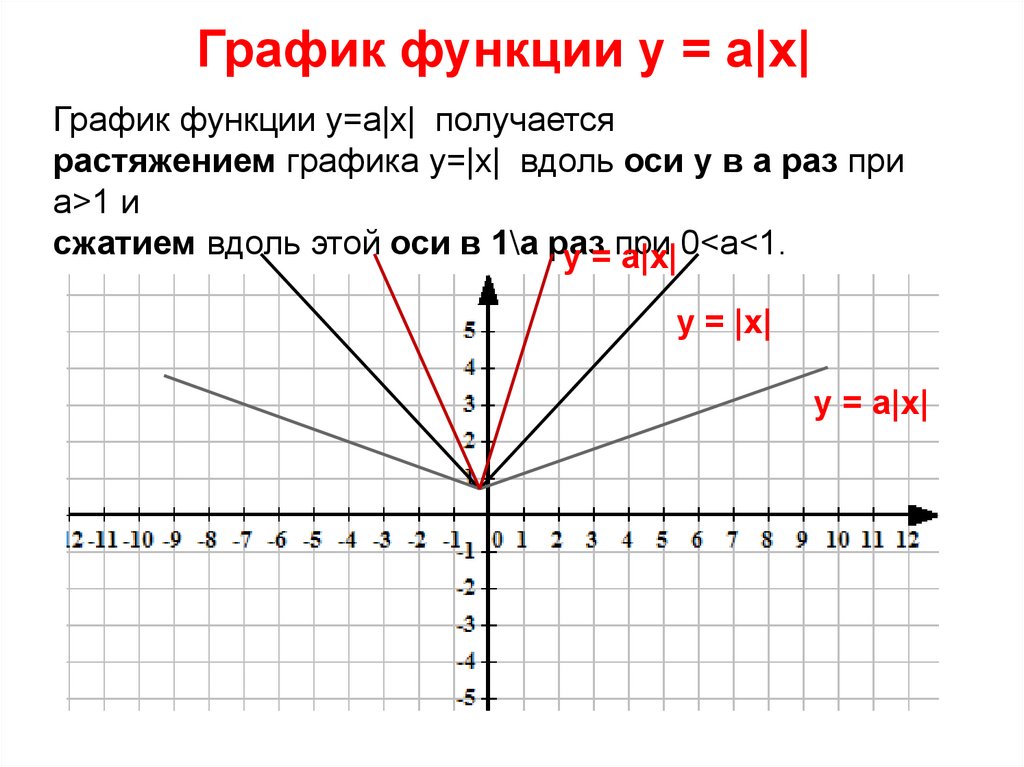
График функции у = а|х|
График функции у=а|х| получается
растяжением графика у=|х| вдоль оси у в а раз при
а>1 и
сжатием вдоль этой оси в 1\а раз
у = при
а|х| 0<a<1.
у = |х|
у = а|х|

17.

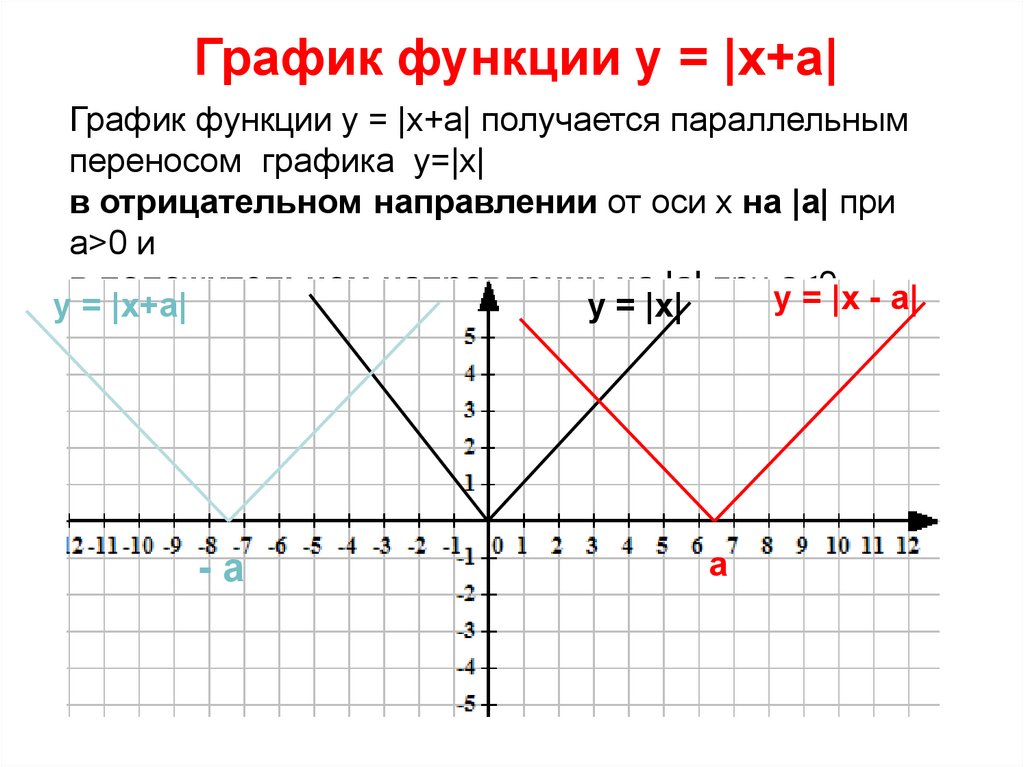
График функции у = |х+а|
График функции у = |x+a| получается параллельным
переносом графика y=|x|
в отрицательном направлении от оси х на |а| при
а>0 и
в положительном направлении на |a| при уa<0.
= |х - а|
у = |х+а|
у = |х|
-а
а

18.

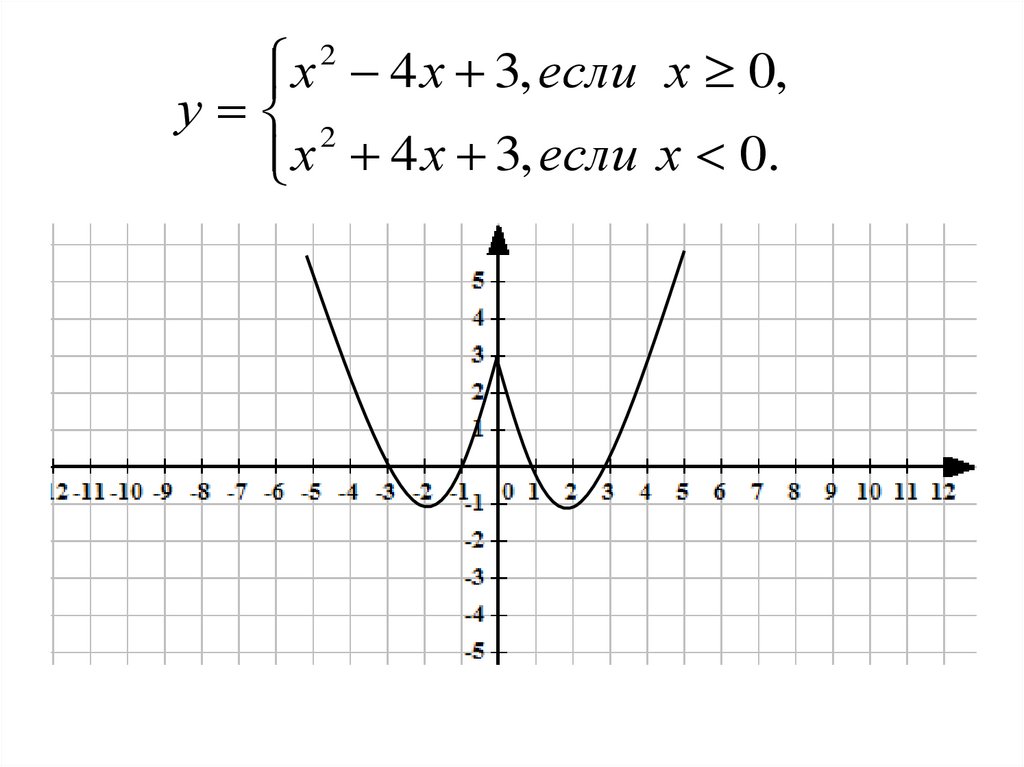
Построить график функции у = х² - 4|х| + 3.
1 способ.
Раскрываем |х| = х при х≥0, получаем график у = х² - 4х + 3.
При х<0, |х|= - х, получаем график у = х² + 4х + 3.
2
х 4 х 3, если х 0,
у 2
х 4 х 3, если х 0.
Строим кусочно – заданную функцию по алгоритму:
1. Находим вершину параболы для каждой функции.
2. Находим точки пересечения каждой параболы с осью х.
3. Строим параболы по заданным условиям.

19.

х 4 х 3, если х 0,
у 2
х 4 х 3, если х 0.
2

20.

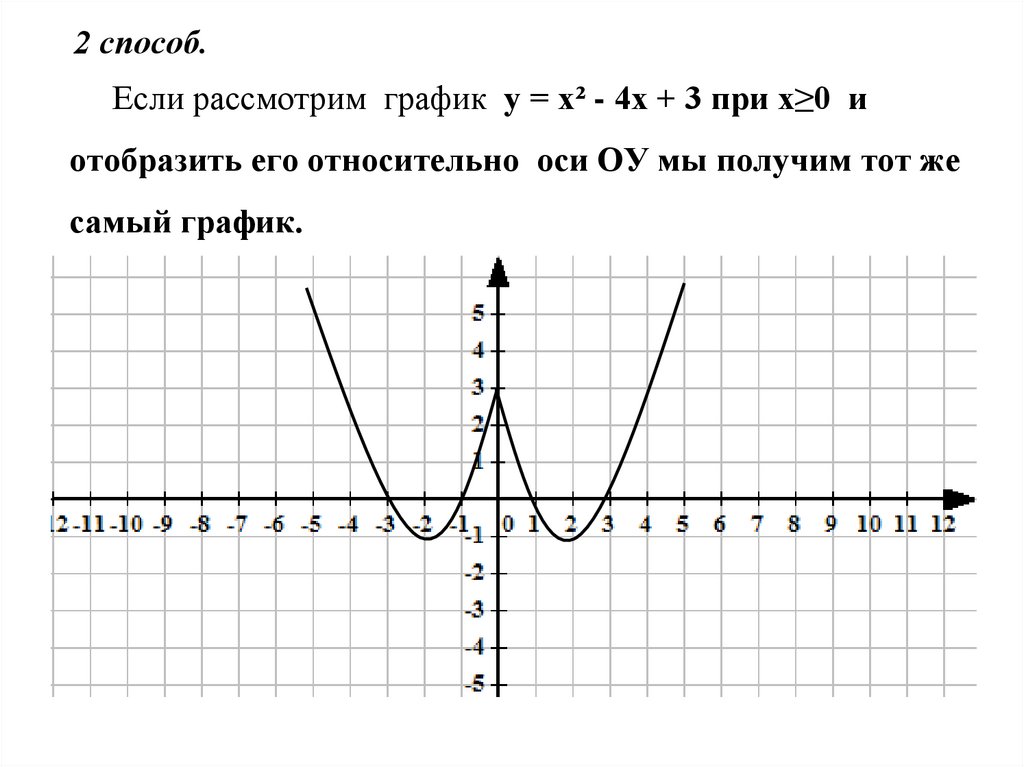
2 способ.
Если рассмотрим график у = х² - 4х + 3 при х≥0 и
отобразить его относительно оси ОУ мы получим тот же
самый график.

21.

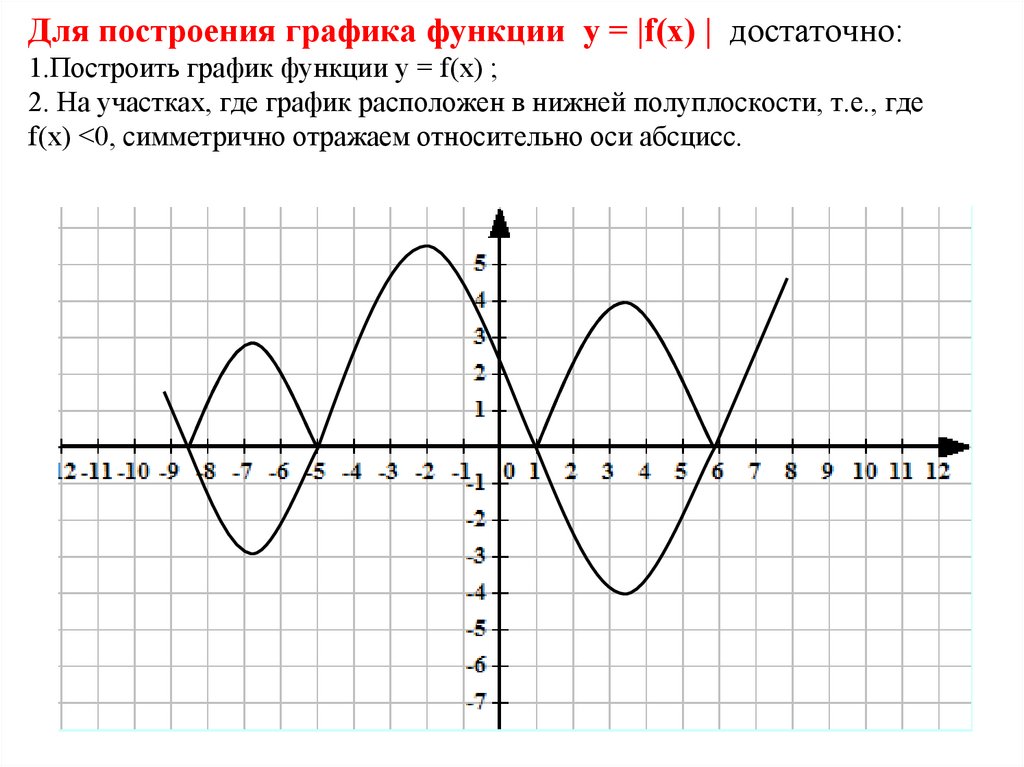
Для построения графика функции у = |f(х) | достаточно:
1.Построить график функции у = f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где
f(х) <0, симметрично отражаем относительно оси абсцисс.

22.

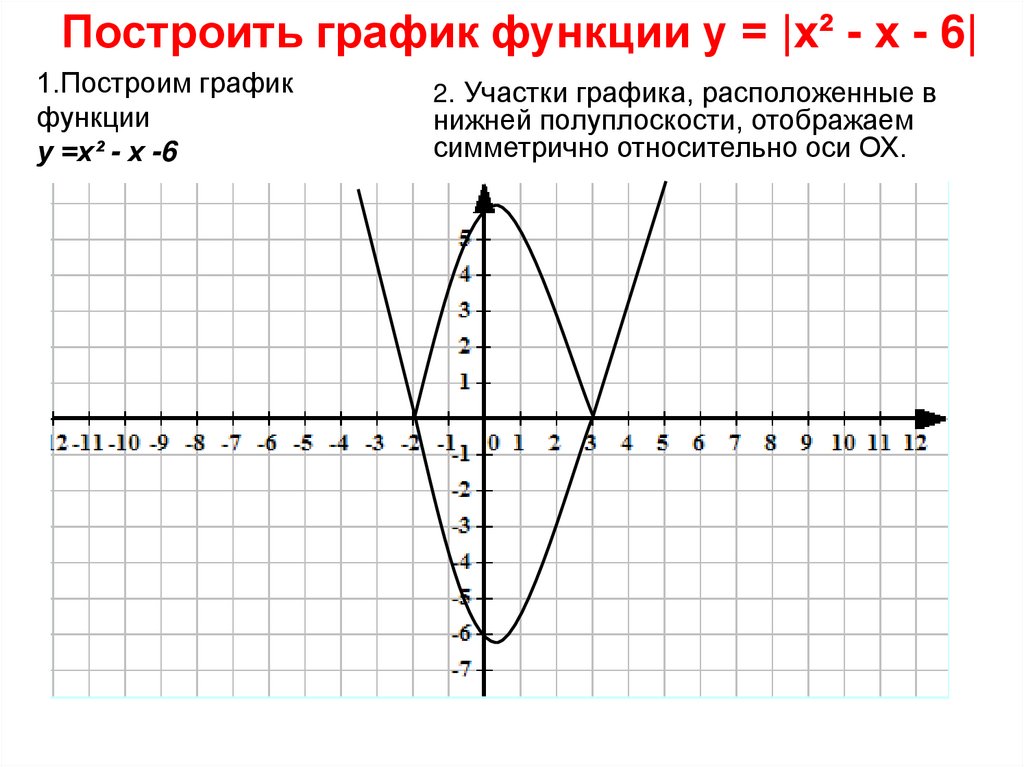
Построить график функции у = |х² - х - 6|
1.Построим график
функции
у =х² - х -6
2. Участки графика, расположенные в
нижней полуплоскости, отображаем
симметрично относительно оси ОХ.

23.

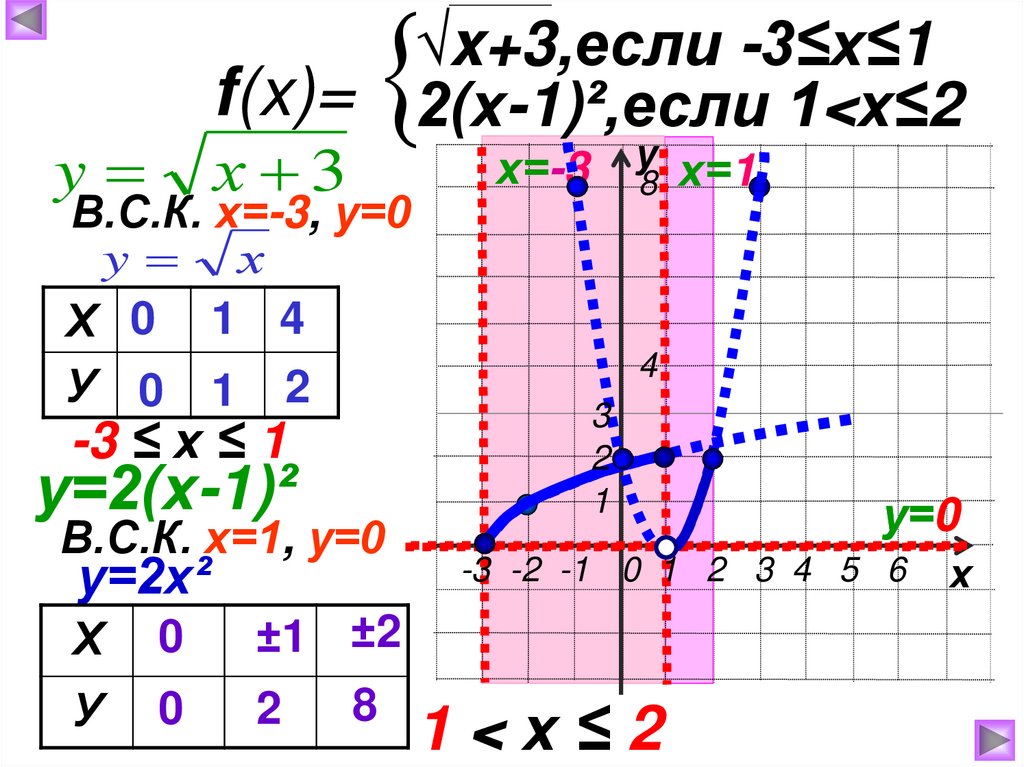
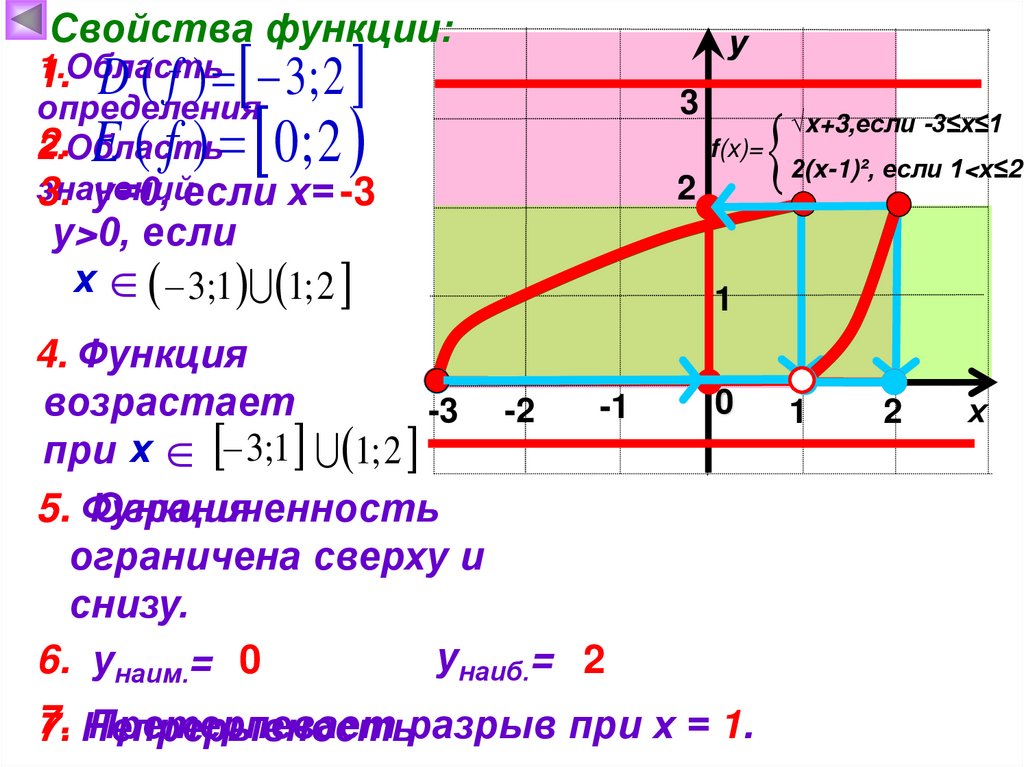
Постройте график функции
√x+3,если -3≤х≤1
f(x)= 2(х-1)²,если 1<х≤2
и опишите её свойства.

24.

√x+3,если -3≤х≤1
f(x)= 2(х-1)²,если 1<х≤2
у х=1
х=-3
х 3
8
y
В.С.К. х=-3, у=0
y х
Х 0 1 4
У 0 1 2
-3 ≤ х ≤ 1
у=2(х-1)²
В.С.К. х=1, у=0
у=2х²
Х
0
У
0
±1 ±2
8
2
4
3
2
1
у=0
-3 -2 -1 0 1 2 3 4 5 6
1<х≤2
х

25.

Свойства функции:
1.Область
1. D ( f ) 3; 2
определения
у
E ( f ) 0; 2
3
2.
2.Область
значений
3. у=0, если х= -3
f(x)=
2
у>0, если
х 3;1 1; 2
4. Функция
возрастает
-3
при х 3;1 1; 2
√x+3,если -3≤х≤1
2(х-1)², если 1<х≤2
1
-2
-1
0
5. Функция
Ограниченность
ограничена сверху и
снизу.
унаиб.= 2
6. унаим.= 0
7. Непрерывность
Претерпевает разрыв при х = 1.
1
2
х

26. Домашнее задание: 1. Изучить материал презентации и записать примеры в тетрадь. 2. Построить график функции у = |х² - 4х + 3| и

прислать на почту
madam.korinenko@mail.ru до 23.02.2025