Similar presentations:
Типы интегралов
1.
Укажем некоторые типы интегралов, которые удобно вычислятьметодом интегрирования по частям.
1.Интегралы вида
P( x) e dx, P( x) sin kxdx, P( x) cos kxdx,
kx
где P( x) многочлен, k число.
Удобно положить u P( x) ,
а за dv обозначить все остальные сомножители.
2.
2.Интегралы видаP( x)arcsin xdx, P( x)arccos xdx, P( x)ln xdx,
P( x)arctgxdx, P( x)arcctgxdx.
Удобно положить P( x) dv, а за
сомножители.
u
обозначить остальные
3.
3.Интегралы видаe sin bxdx, e cos bxdx,
ax
Где a и b - числа. За u
ax
можно принять функцию u e
ax
.
3x
(2
x
1)
e
dx.
Пример № 1. Найти
u 2x 1
(можно положить С=0)
Решение: Пусть
dv e3 x dx
du 2dx
v e3 x dx 1 e3 x
3
Следовательно по формуле интегрирования по частям:
1 3x 1 3x
1
2 3x
3x
(2 x 1)e dx (2 x 1) 3e 3e 2dx 3 (2 x 1)e 9 e C
3x
4.
Пример №2. Найти ln xdx.Решение: Пусть u ln x
dv dx
1
du x dx
v dx x
1
Поэтому ln xdx x ln x x dx x ln x x C
x
5.
Пример №3. НайтиРешение: Пусть
2 x
x
e dx
u x2
.Поэтому
x
dv
e
dx
du 2 xdx
x
v e
2 x
2 x
x
x
e
dx
x
e
2
e
xdx.
Для вычисления интеграла e x xdx снова применим метод
u x
интегрирования по частям :
dv e x dx
du dx
x
x
v e dx e
Значит,
Поэтому
x
x
x
x
x
e
xdx
x
e
e
dx
x
e
e
C
2 x
2 x
x
x
x
e
dx
x
e
2(
x
e
e
C
)
6.
Пример. Найти arctgxdxРешение:Пусть u arctgx .
dv dx
1
du 1 x 2 dx
v dx x
x
1 d (1 x 2 )
Поэтому arctgxdx x arctgx
dx x arctgx
2
2
1 x
2 1 x
1
x arctgx ln(1 x 2 ) C
2



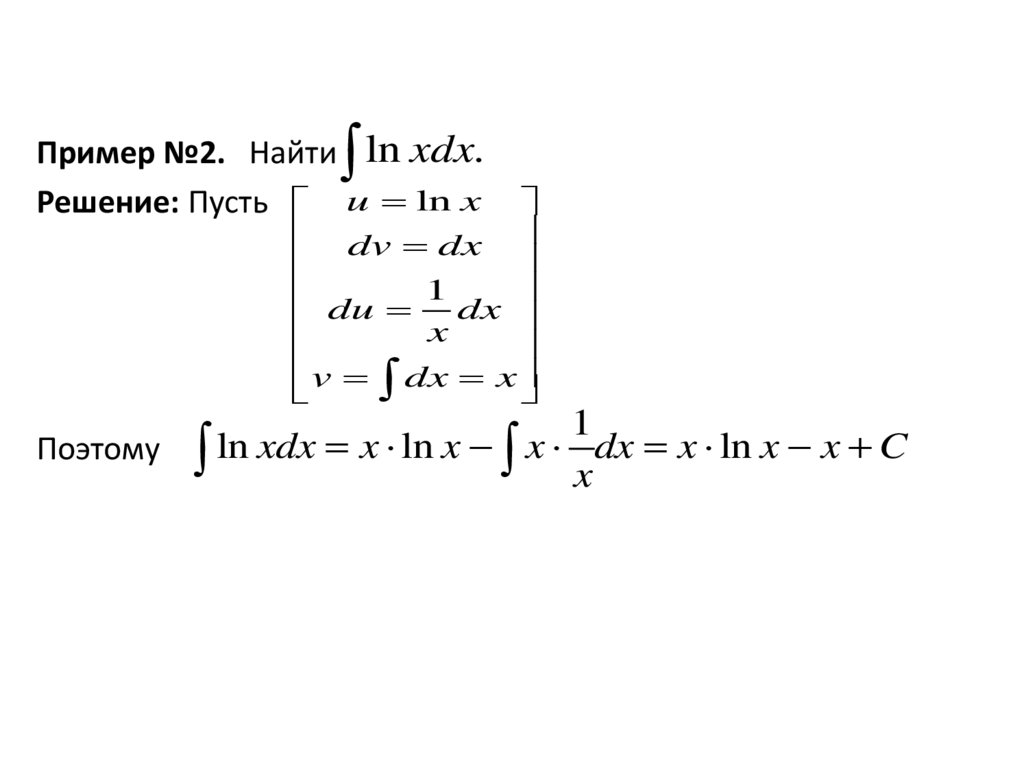


 mathematics
mathematics








