Изгиб. Напряжения. Расчеты на прочность

1.

Изгиб. Напряжения.
Расчеты на прочность

2.

Нормальные напряжения при изгибе
В теории плоского изгиба, для упрощения решения задачи определения
нормальных напряжений, на основании натурных испытаний, приняты
следующие допущения:
•При изгибе продольные сечения балки искривляются по дуге окружности;
•Поперечные сечения плоские до изгиба, остаются плоскими и после изгиба;
•Поперечные сечения пересекаются с продольными волокнами под прямым
углом.
Задача определения нормальных напряжений при изгибе является
статически неопределимой и для ее решения необходимо рассмотреть три
стороны задачи
Статическая (ССЗ)
Геометрическая (ГСЗ)
Физическая (ФСЗ)
Синтез

3. Статическая сторона задачи

2 участок
1 участок
а
3 участок
l
a
Опорные реакции
Rb
Ra
m Fa R l F a l 0
A
F
F
B
m F (a l ) R l Fa 0
B
z1
z2
A
F a l Fa
RA
F
l
z3
Эпюра поперечных сил
F a l Fa
RB
F
l
F
Проверка
Эпюра изгибающих моментов
F
F F R R F F F F F 0
кy
Fa
A
B

4. Статическая сторона задачи

2 участок
1 участок
а
3 участок
l
Эпюры поперечных сил и изгибающих моментов
a
1 участок 0 ≤ z1 ≥ a
Rb
Ra
F При z1=а, М1(а)=F·a
F
Q1 F
При z1=0, М1(0)=0
2 участок a ≤ z2 ≥ (a+l)
z1
z2
M 2 F z 2 F z 2 a
z3
M1 F z1
Q2 F RA F F 0
При z2=а, М2(а)=F·a
При z2=а+l, М2(а+l)=F·(a+l) -F(a+l-a)=Fa
Эпюра поперечных сил
F
3 участок (a+l) ≤ z3 ≥ (2a+l)
Эпюра изгибающих моментов
Fa
Fa
F
Q3 F RA RB F F F F
M 3 F z3 F z3 a F z3 a l
При z3=а+l, М3(а+l)=F·(a+l) -F(a+l-a)=Fa
При z3=2а+l, М2(2а+l)=F·(2a+l) -F(2a+l-a)=0

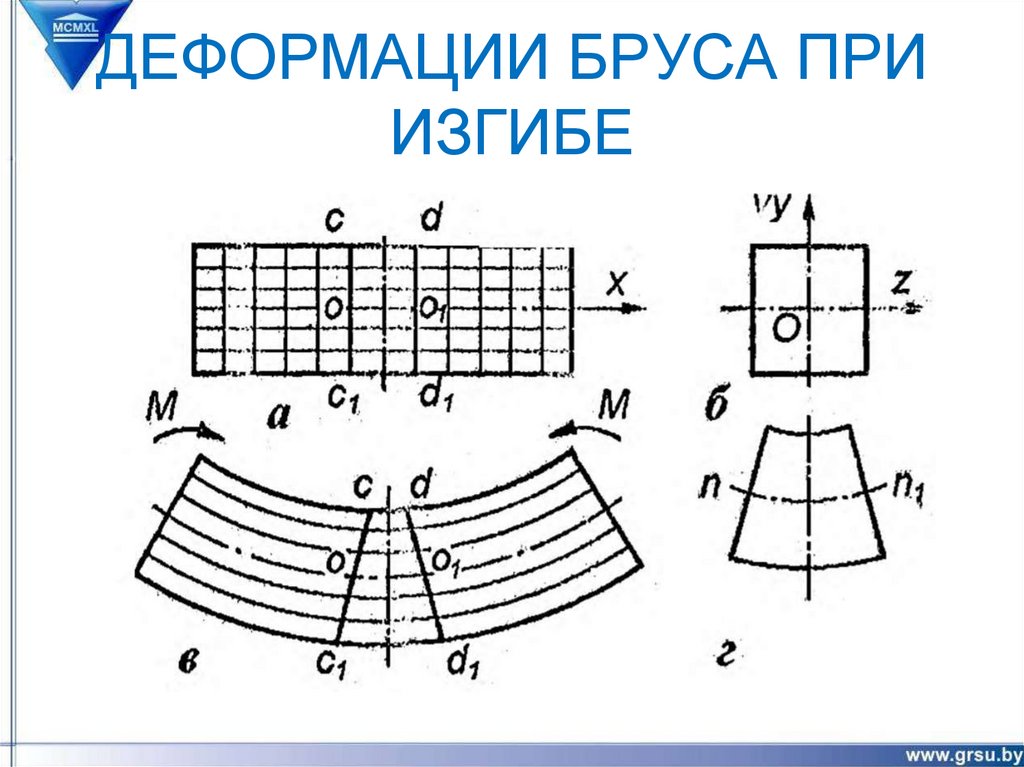
5. ДЕФОРМАЦИИ БРУСА ПРИ ИЗГИБЕ

6. Статическая сторона задачи

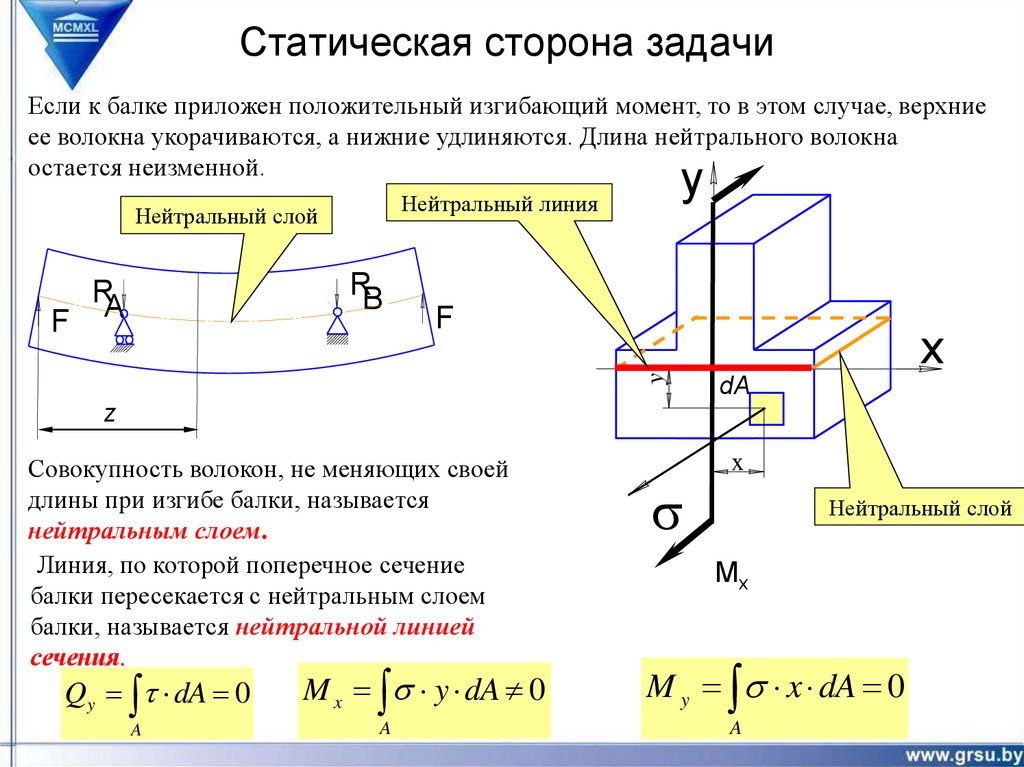
Если к балке приложен положительный изгибающий момент, то в этом случае, верхние
ее волокна укорачиваются, а нижние удлиняются. Длина нейтрального волокна
остается неизменной.
Нейтральный слой
RB
F
x
y
RA
F
y
Нейтральный линия
dA
z
Совокупность волокон, не меняющих своей
длины при изгибе балки, называется
нейтральным слоем.
Линия, по которой поперечное сечение
балки пересекается с нейтральным слоем
балки, называется нейтральной линией
сечения.
Qy dA 0
A
M x s y dA 0
A
x
s
Нейтральный слой
Мx
M y s x dA 0
A

7. Геометрическая сторона задачи

Длина отрезка на нейтральном слое
Центр
изгиба
a0b0 dz
Длина отрезка на слое удаленном от нейтрального
на расстояние y
a1b1 y
Удлинение отрезка после деформации
ab a1b1 a0b0 y y
Относительная деформация
dz
F
a0
a1
b0
b1
F
y
a1b1 a0 b0 y
a0 b0

8. Физическая сторона задачи

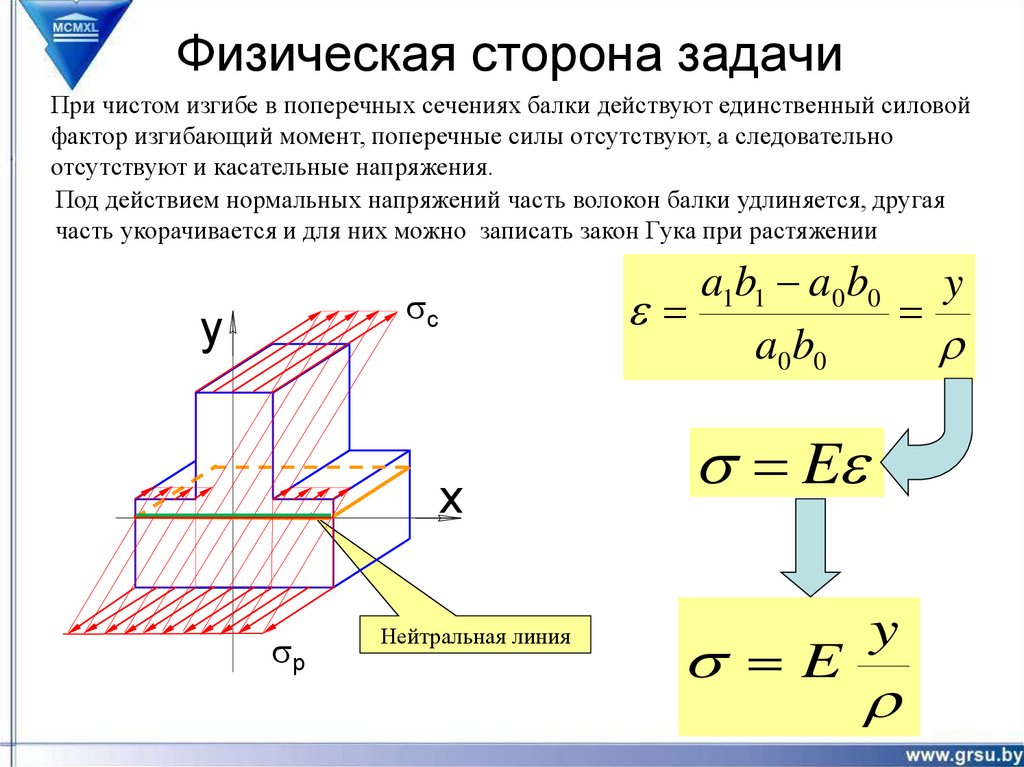
При чистом изгибе в поперечных сечениях балки действуют единственный силовой
фактор изгибающий момент, поперечные силы отсутствуют, а следовательно
отсутствуют и касательные напряжения.
Под действием нормальных напряжений часть волокон балки удлиняется, другая
часть укорачивается и для них можно записать закон Гука при растяжении
a1b1 a0 b0 y
a0 b0
sс
y
x
sр
Нейтральная линия
s E
s E
y

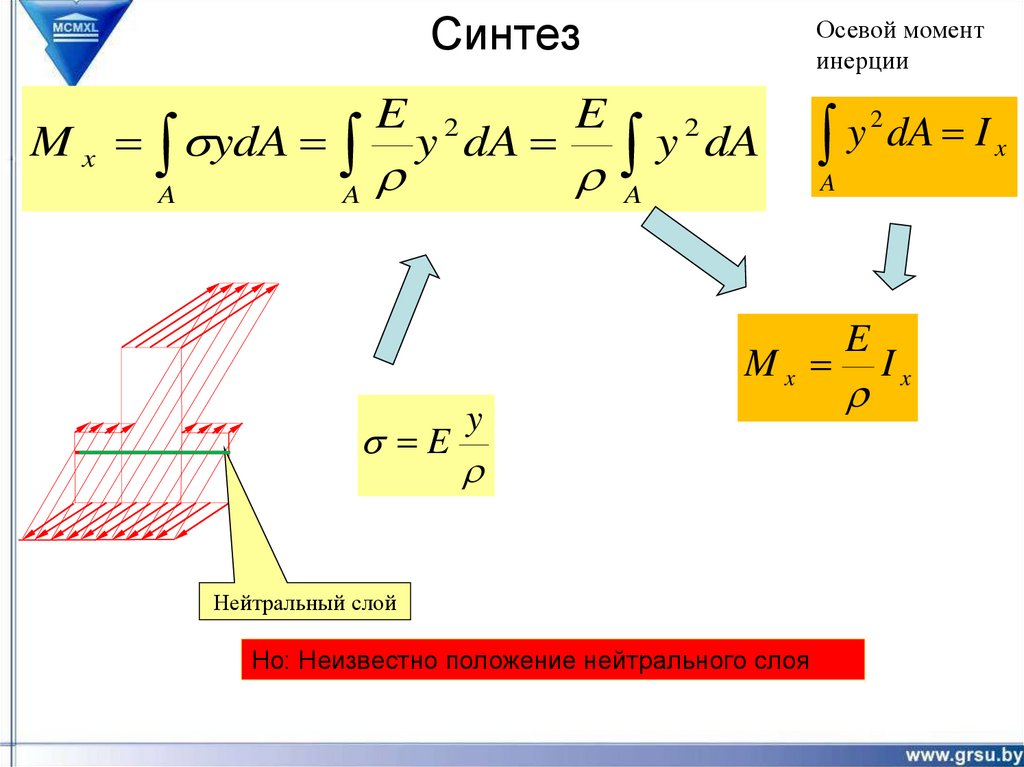
9. Синтез

M x sydA
A
A
E
y dA
2
Осевой момент
инерции
E
y dA
2
A
2
y
dA I x
A
Mx
s E
y
Нейтральный слой
Но: Неизвестно положение нейтрального слоя
E
Ix

10. Синтез

При чистом изгибе продольная сила равна нулю
N s dA 0
s E
A
N E
A
y
dA
E
y
ydA 0
A
E 0
ydA 0
A
ydA S 0
x
A
Статический момент относительно центральных осей равен нулю
Нейтральный слой проходит через центр тяжести сечения

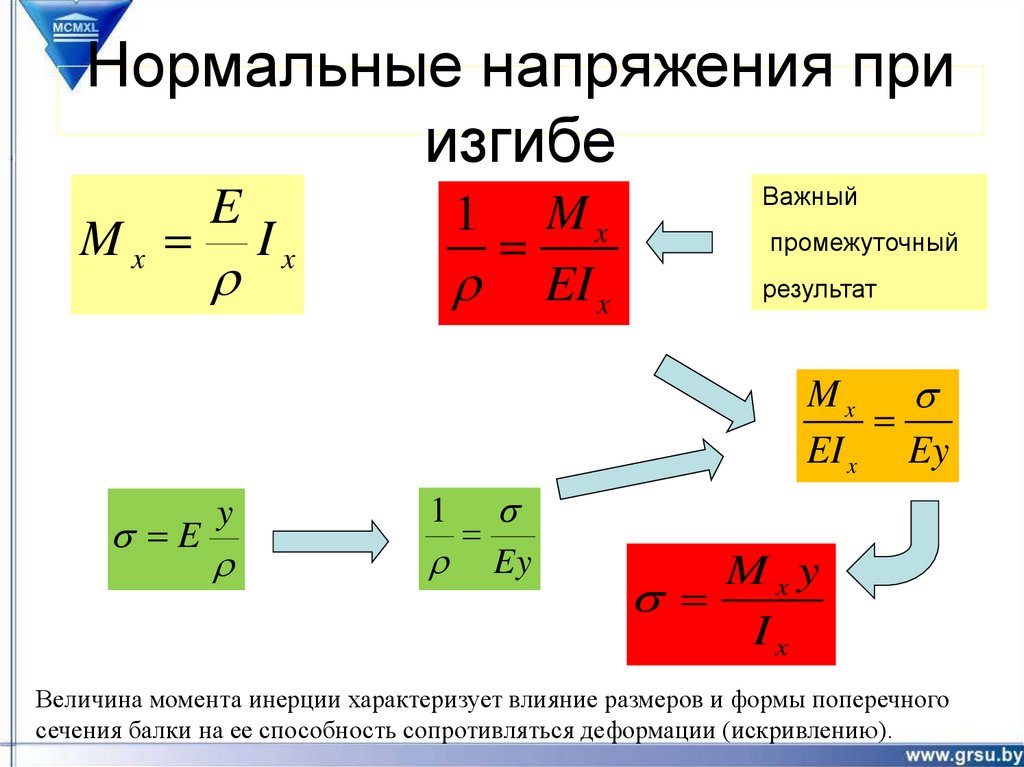
11. Нормальные напряжения при изгибе

Mx
E
Mx
EI x
1
Ix
Важный
промежуточный
результат
Mx s
EI x Ey
s E
y
s
Ey
1
Mxy
s
Ix
Величина момента инерции характеризует влияние размеров и формы поперечного
сечения балки на ее способность сопротивляться деформации (искривлению).

12.

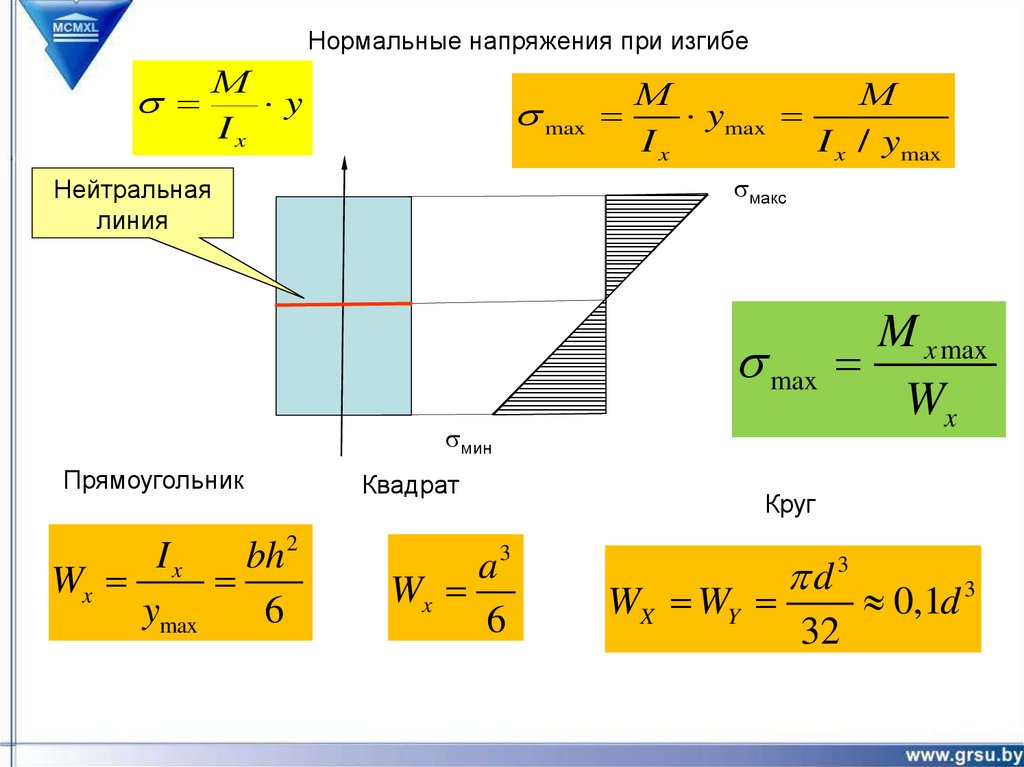
Нормальные напряжения при изгибе
М
s
y
Ix
М
М
s max
ymax
Ix
I x / ymax
sмакс
Нейтральная
линия
sмин
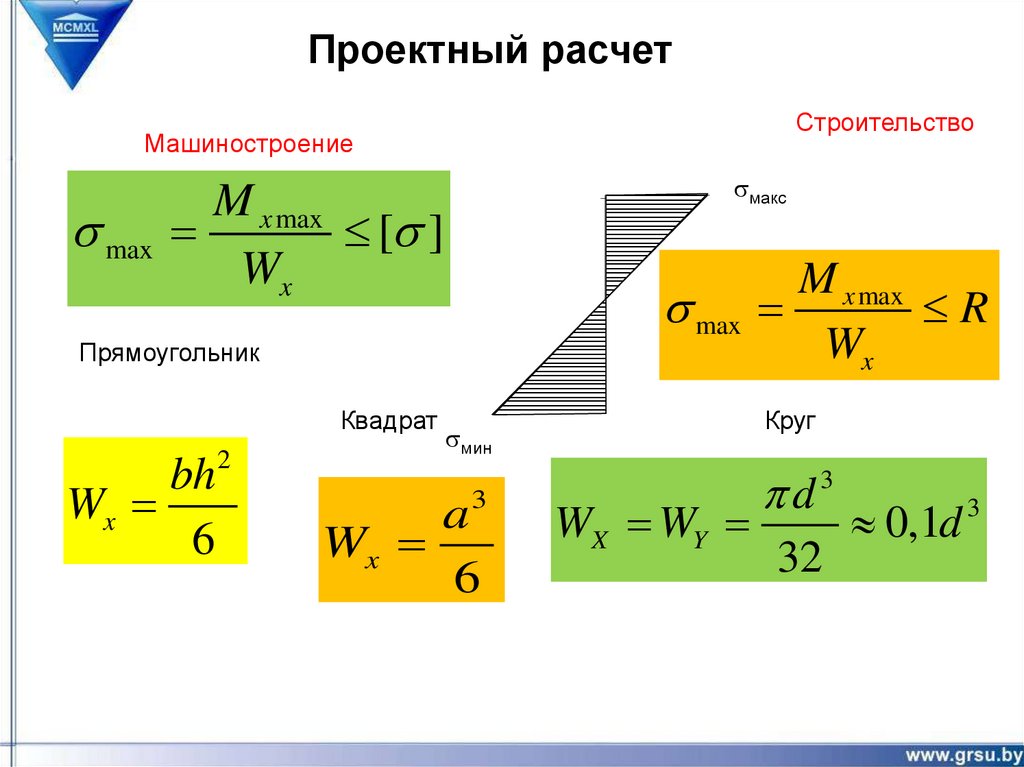
Прямоугольник
Ix
bh2
Wx
ymax
6
Квадрат
a3
Wx
6
M x max
s max
Wx
Круг
WX WY
d3
32
0,1d 3

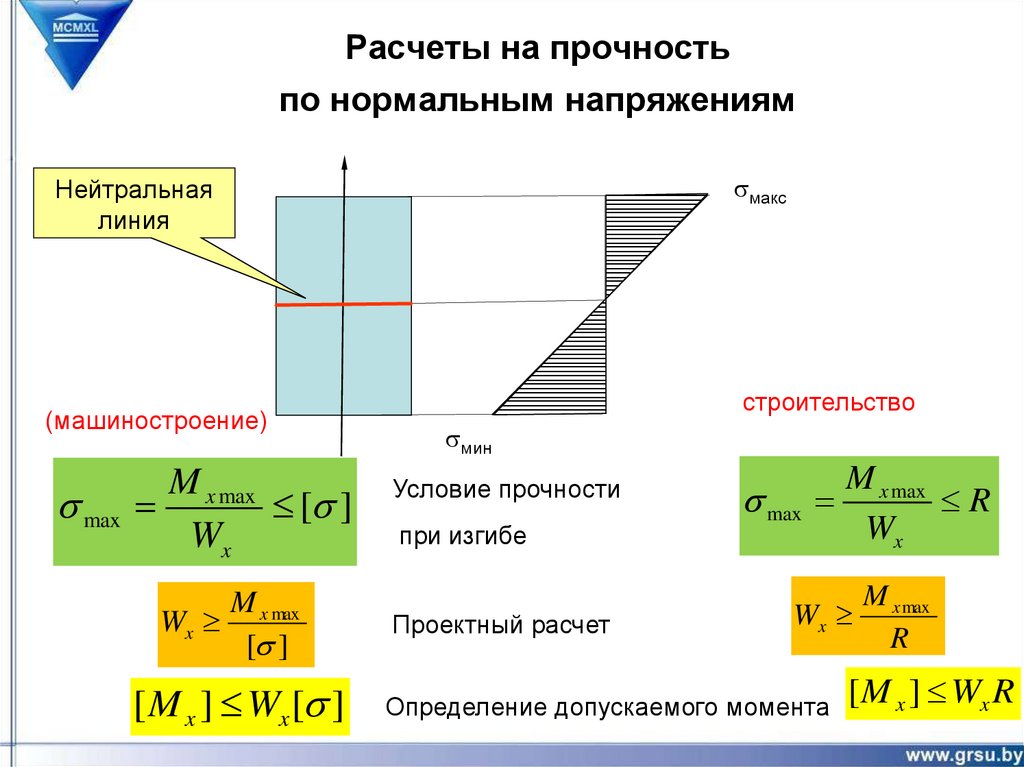
13. Расчеты на прочность по нормальным напряжениям

sмакс
Нейтральная
линия
(машиностроение)
M x max
s max
[s ]
Wx
M
Wx x max
[s ]
[ M x ] Wx [s ]
строительство
sмин
Условие прочности
при изгибе
Проектный расчет
M x max
s max
R
Wx
Wx
Определение допускаемого момента
M x max
R
[ M x ] Wx R

14.

Проектный расчет
Строительство
Машиностроение
sмакс
M x max
s max
[s ]
Wx
M x max
s max
R
Wx
Прямоугольник
Квадрат
bh 2
Wx
6
Круг
sмин
a3
Wx
6
WX WY
d
3
32
0,1d
3

15.

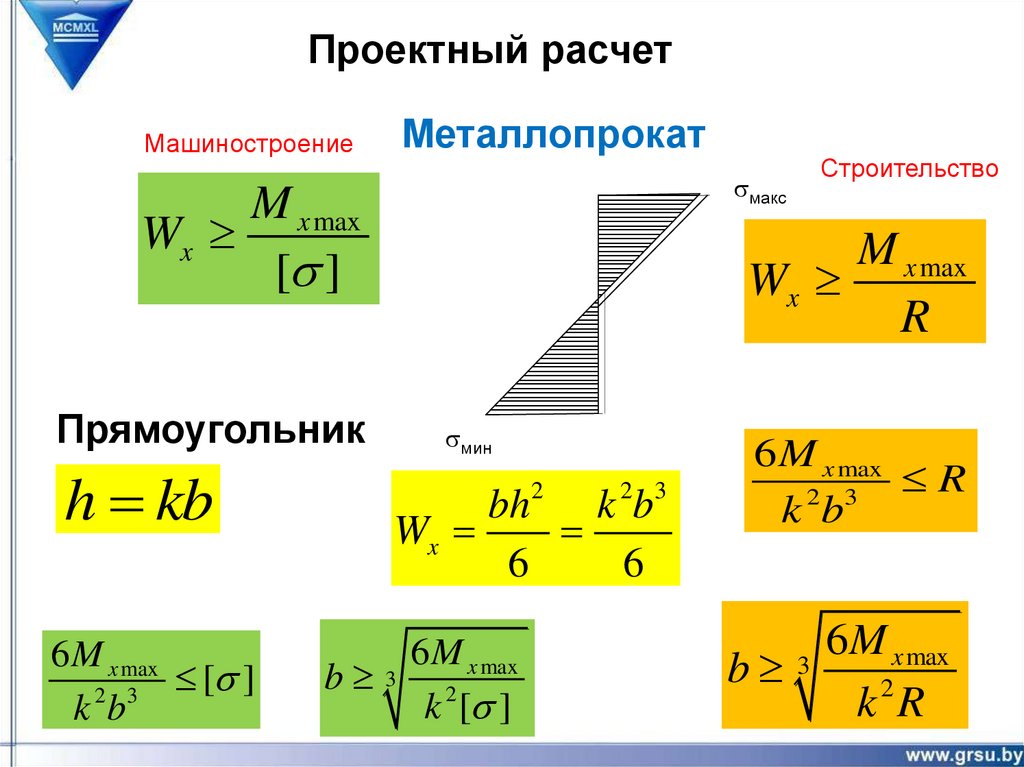
Проектный расчет
Машиностроение
Металлопрокат
sмакс
M x max
Wx
[s ]
Прямоугольник
h kb
6 M x max
[s ]
2 3
k b
Строительство
M x max
Wx
R
sмин
bh 2 k 2b3
Wx
6
6
6M x max
b 3 2
k [s ]
6 M x max
R
2 3
k b
6
M
x max
b 3
k 2R

16.

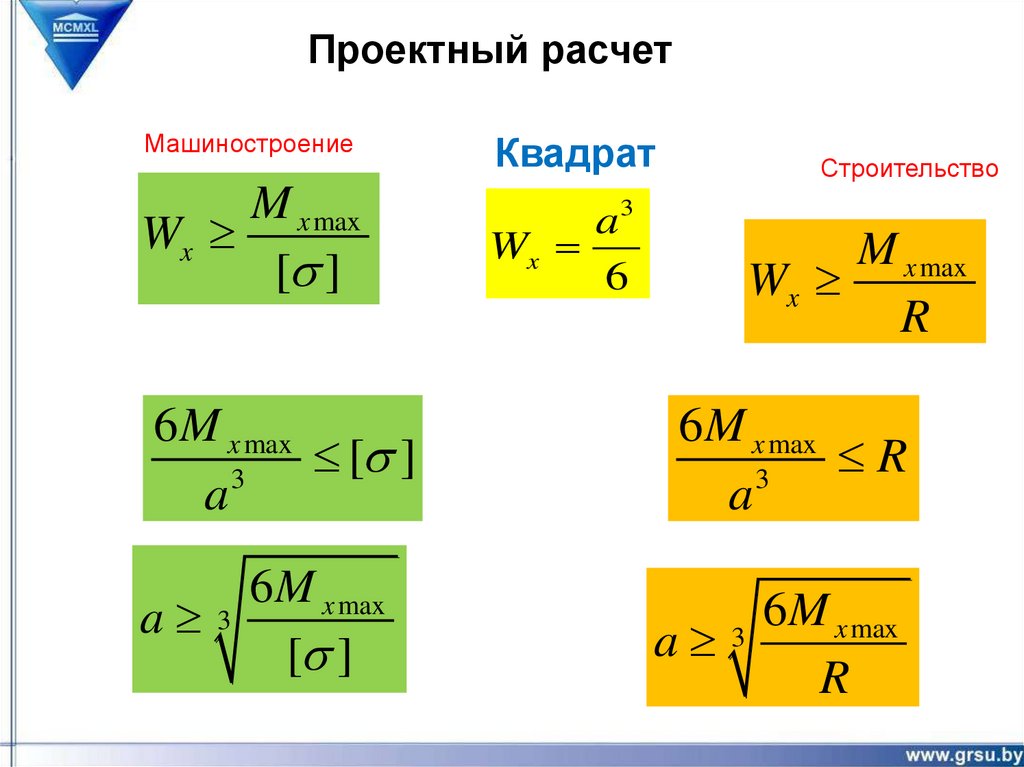
Проектный расчет
Машиностроение
Квадрат
M x max
Wx
[s ]
a3
Wx
6
Строительство
M x max
Wx
R
6 M x max
[s ]
3
a
6 M x max
R
3
a
6 M x max
a 3
[s ]
6
M
x max
3
a
R

17.

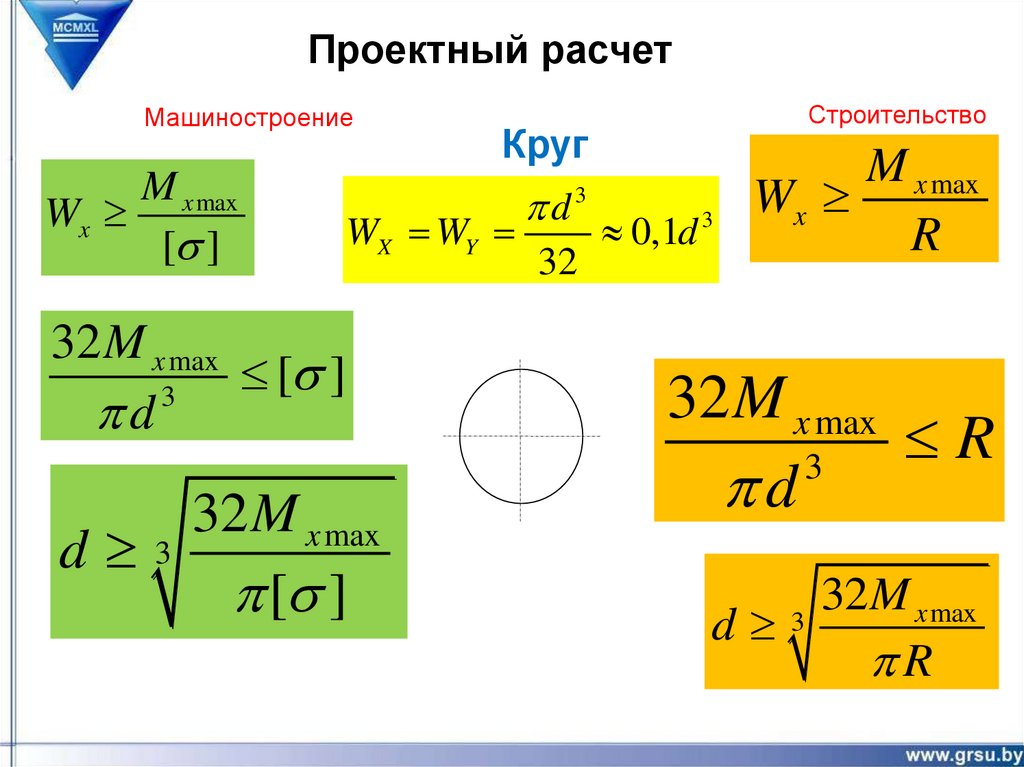
Проектный расчет
Машиностроение
M x max
Wx
[s ]
Круг
WX WY
32 M x max
[s ]
3
d
32 M x max
d 3
[s ]
Строительство
d3
32
0,1d 3
M x max
Wx
R
32 M x max
R
3
d
32M x max
d
R
3

18.

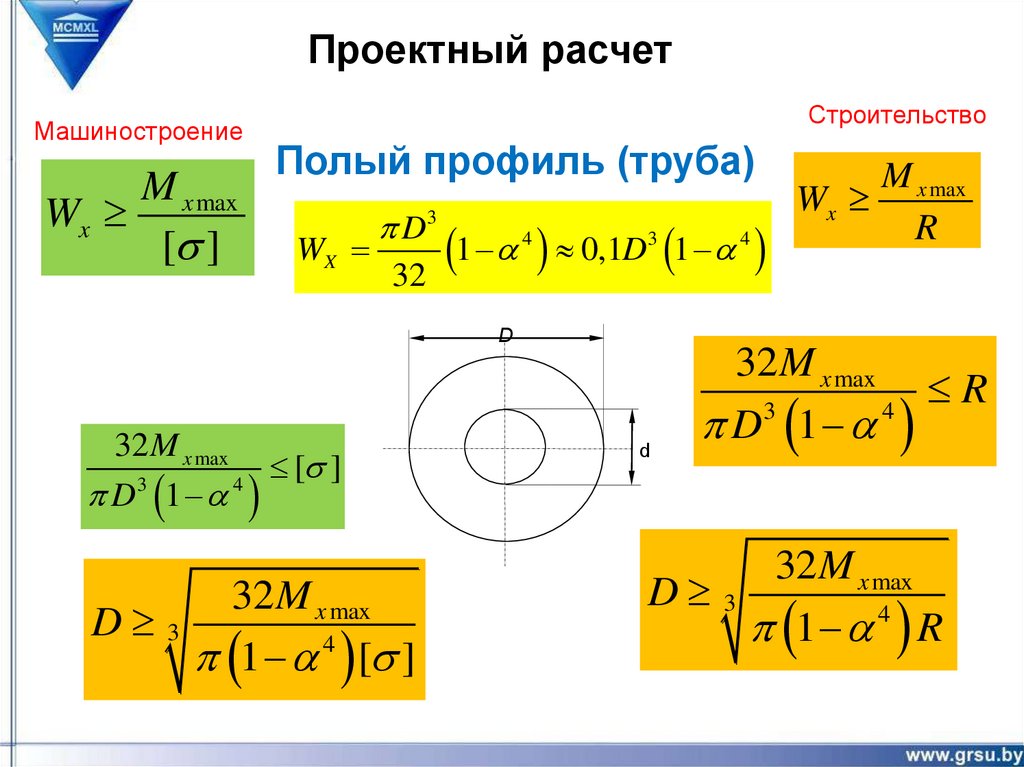
Проектный расчет
Машиностроение
M x max
Wx
[s ]
Строительство
Полый профиль (труба)
WX
D3
1 0,1D 1
32
4
3
4
M x max
Wx
R
D
32 M x max
[s ]
3
4
D 1
32M x max
D 3
1 4 [s ]
d
32M x max
R
3
4
D 1
32M x max
D 3
1 4 R

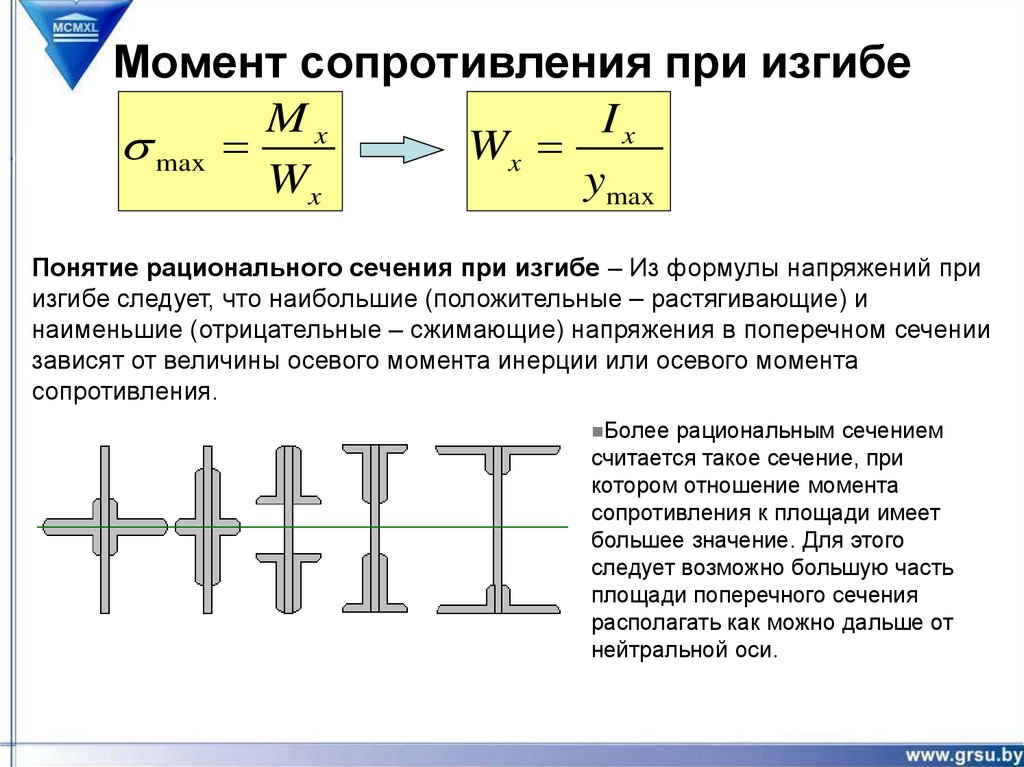
19. Момент сопротивления при изгибе

Mx
s max
Wx
Ix
Wx
ymax
Понятие рационального сечения при изгибе – Из формулы напряжений при
изгибе следует, что наибольшие (положительные – растягивающие) и
наименьшие (отрицательные – сжимающие) напряжения в поперечном сечении
зависят от величины осевого момента инерции или осевого момента
сопротивления.
Более рациональным сечением
считается такое сечение, при
котором отношение момента
сопротивления к площади имеет
большее значение. Для этого
следует возможно большую часть
площади поперечного сечения
располагать как можно дальше от
нейтральной оси.

20.

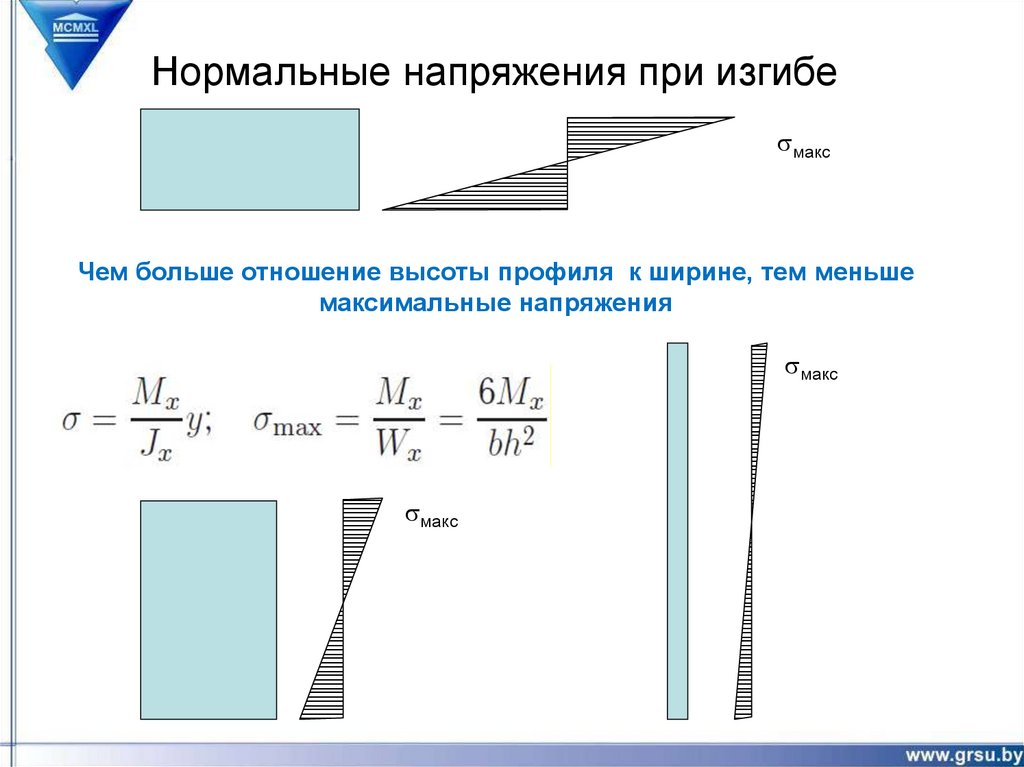
Нормальные напряжения при изгибе
sмакс
Чем больше отношение высоты профиля к ширине, тем меньше
максимальные напряжения
sмакс
sмакс

21.

Особенности изгиба чугуна и бетона
Некоторые материалы (чугун, бетон, кирпичная кладка и др.) плохо работают на
растяжение, но хорошо на сжатие.
Необходима проверка на прочность отдельно по растянутым волокнам и по сжатым
волокнам, особенно если конструкция не симметрична относительно нейтральной
оси.
машиностроение
строительство
M x max
s max р
[sр ]
Wv
M x max
s max t
Rt
Wx
M x max
s max c
[sc ]
Wv
M x max
s max c
Rc
Wv

22.

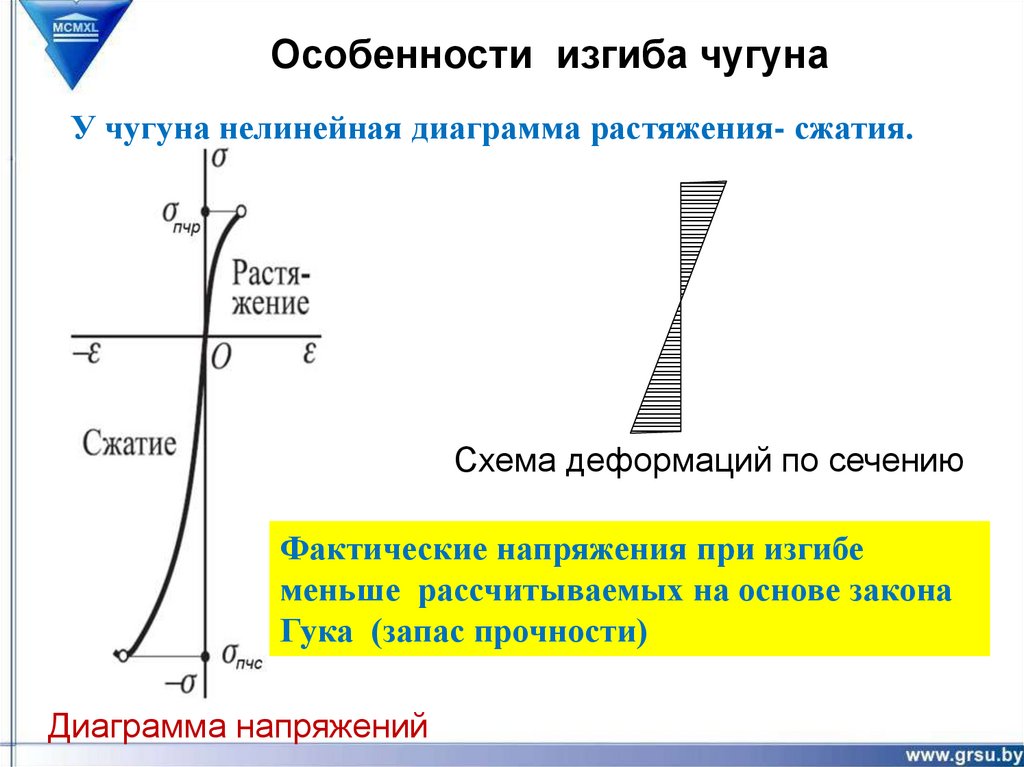
Особенности изгиба чугуна
У чугуна нелинейная диаграмма растяжения- сжатия.
Схема деформаций по сечению
Фактические напряжения при изгибе
меньше рассчитываемых на основе закона
Гука (запас прочности)
Диаграмма напряжений

23.

Особенности изгиба железобетона
Строительство
Бетон плохо работает на растяжение, но хорошо на сжатие.
Необходимо:
1. Армировать материал в зоне растянутых волокон
(железобетон);
2.Создавать предварительно напряженный бетон
(различные способы)
ВАЖНО: Правильно уложить арматуру:
в нейтральный слой- нет эффекта!!!
в сжатый слой- нет эффекта!!!

24. Примеры неудачного конструирования

25. Примеры неудачного конструирования

26. Примеры неудачного конструирования

27. Примеры неудачного конструирования

28. Примеры удачного конструирования

29. Примеры удачного конструирования

30.

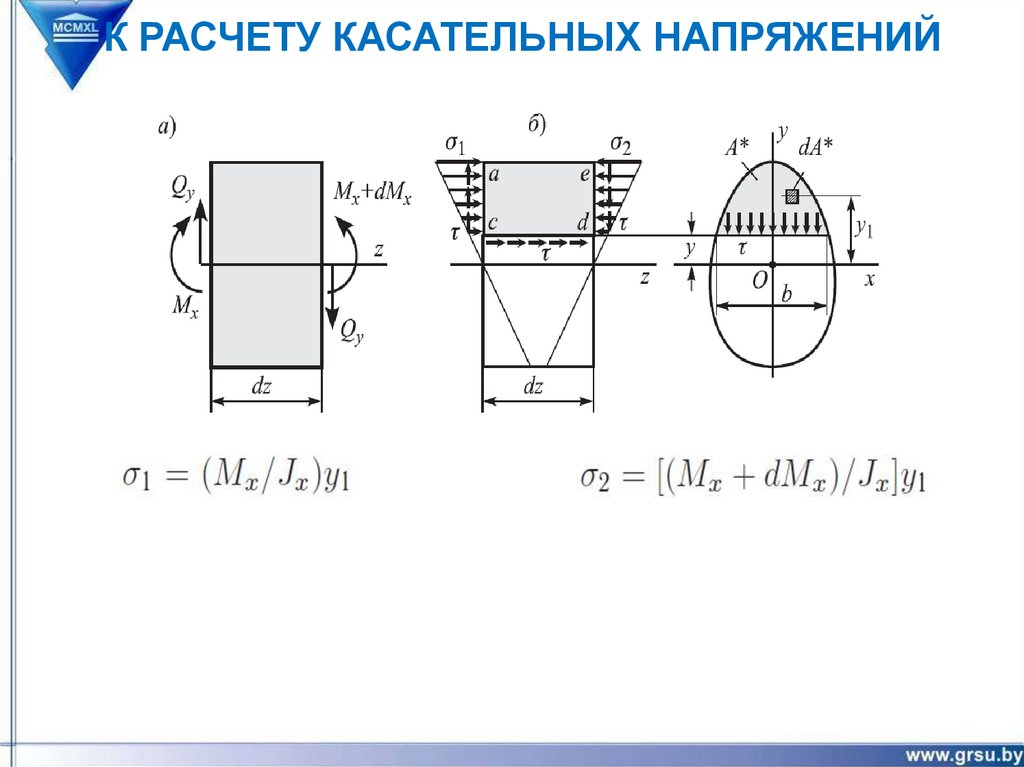
К РАСЧЕТУ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ

31.

К РАСЧЕТУ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ

32.

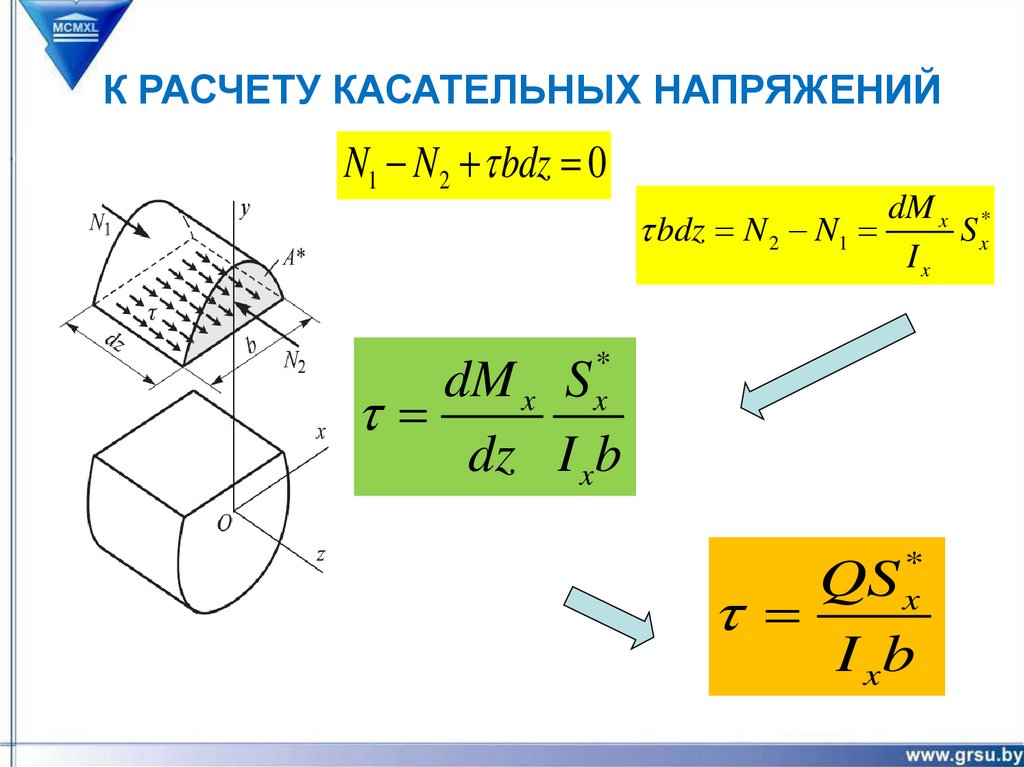
К РАСЧЕТУ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ

33.

К РАСЧЕТУ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
N1 N2 bdz 0
dM x *
bdz N 2 N1
Sx
Ix
*
x
dM x S
dz I xb
*
x
QS
I xb

34.

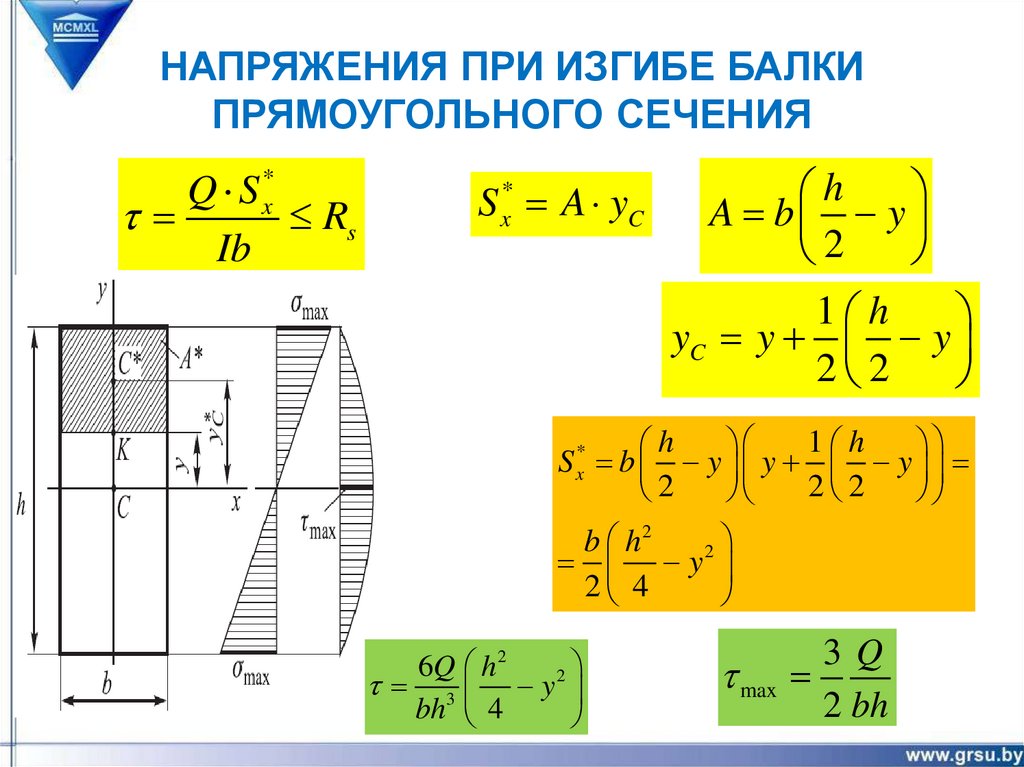
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ БАЛКИ
ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
Q S x*
Rs
Ib
S A yC
*
x
h
A b y
2
1 h
yC y y
2 2
1 h
h
S x* b y y y
2 2
2
b h2
2
y
2 4
6Q h 2
2
3 y
bh 4
3Q
max
2 bh

35.

НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ БАЛКИ
ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ

36. Расчеты на прочность по касательным напряжениям

S 0
Qмакс x
Rs
Ix b
Формула Д. И. Журавского
Где: Qмакс—максимальная по абсолютной величине поперечная сила, Н; Sx0—
статический момент инерции части сечения, мм3; Ix—осевой момент инерции
сечения, мм4; b—ширина сечения по нейтральной линии, мм.
Машиностроение
По высоте прямоугольного
сечения касательные
напряжения меняются по
закону параболы, при этом в
наиболее удаленных от
нейтральной линии точках
поперечного сечения
касательные напряжения
обращаются в нуль и
достигают максимума в
точках на нейтральной линии.
o
QS
[ ]
Ib
макс

37.

ПРИМЕР: СОПОСТАВИТЬ НАПРЯЖЕНИЯ ПРИ
ИЗГИБЕ БАЛКИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ

38.

НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ БАЛКИ
ДВУТАВРОВОГО СЕЧЕНИЯ