Расчеты на прочность при внецентренном действии силы

1. Расчеты на прочность при внецентренном действии силы

F
Внецентренное действие
силы – это частный случай
изгиба с растяжением
(сжатием), который часто
возникает в строительных
конструкциях. Этот вид
деформации создается
силами, линии действия
которых параллельны оси
стержня, но не совпадают
с ней .

2. Внутренние усилия при внецентренном действии силы

Z
Y
F
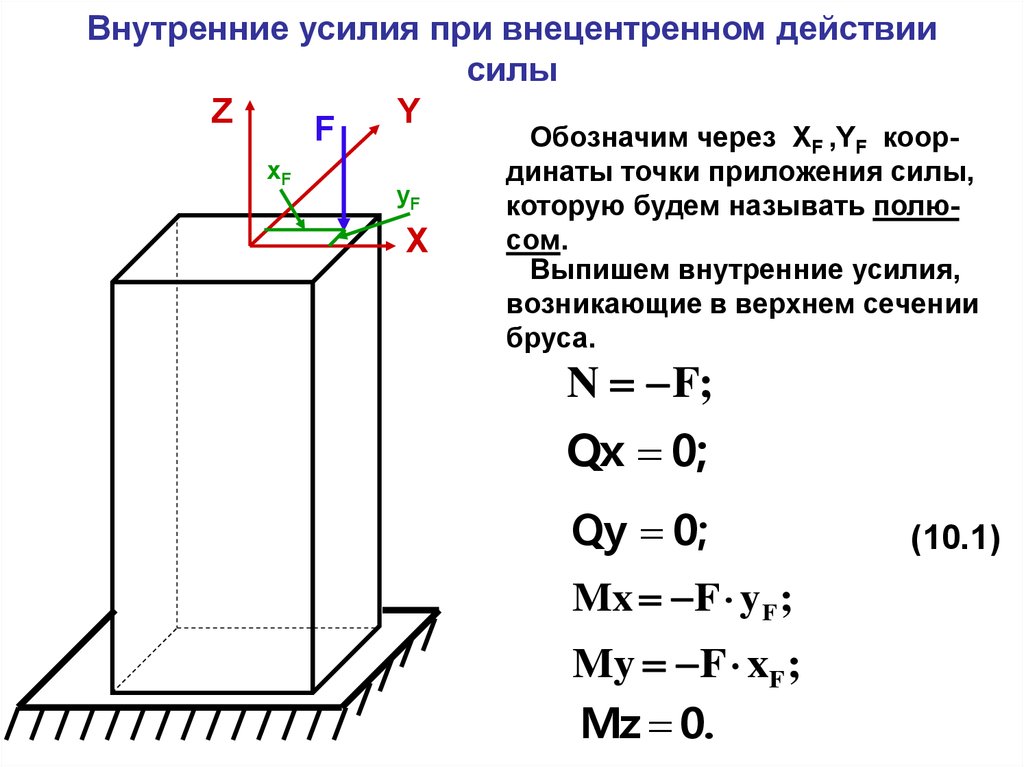
Обозначим через XF ,YF коорxF
yF
X
динаты точки приложения силы,
которую будем называть полюсом.
Выпишем внутренние усилия,
возникающие в верхнем сечении
бруса.
N F;
Qx 0;
Qy 0;
Mx F y F ;
My F xF ;
Mz 0.
(10.1)

3.

Z
F
xF
Y
yF
X
N F; Mx F y F ;
Qx 0; My F xF ;
Qy 0; Mz 0.
Y
xF
yF
X
(10.1)
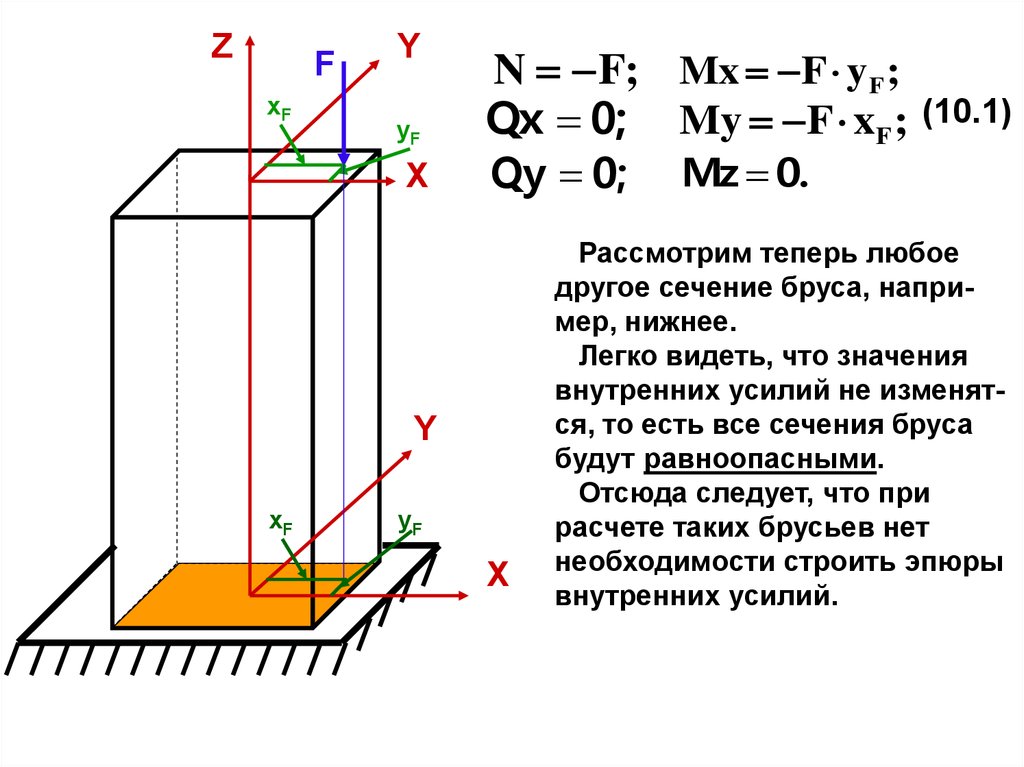
Рассмотрим теперь любое
другое сечение бруса, например, нижнее.
Легко видеть, что значения
внутренних усилий не изменятся, то есть все сечения бруса
будут равноопасными.
Отсюда следует, что при
расчете таких брусьев нет
необходимости строить эпюры
внутренних усилий.

4. Напряжения в поперечном сечении при внецентренном действии силы

Касательные напряжения при внецентренном действии силы
отсутствуют, так как Qx≡Qy≡Mz≡0.
Получим формулу для определения нормальных напряжений.
При изгибе с растяжением (сжатием)
N Mx
My
σz
y
x
A Jx
Jy
Подставим сюда значения внутренних усилий (10.1):
F F yF
F xF
σz
y
x
A
Jx
Jy

5. Вынесем за скобку величину

F F yF
F xF
σz
y
x
A
Jx
Jy
Вынесем за скобку величину
F
A
F yF A
xF A
σ z 1
y
x
A
Jx
Jy
Jx 2 Jy
Теперь учтем, что i
, а также случай действия
; iy
A
A
2
x
растягивающей силы, при которой усилия (10.1) будут положительными, и окончательно получим:
F yF y x F x
σz
1 2 2
A
ix
iy
(10.2)

6.

F yF y x F x
σz
1 2 2
A
ix
iy
(10.2)
В формуле (10.2) xF ,yF -координаты точки приложения силы
(полюса); x,y -координаты точки, в которой определяются
напряжения. Знак плюс в формуле выбирается, когда на стержень
действует растягивающая сила, знак минус –когда сжимающая.
Условие прочности записывается в виде:
σ
max
z
R

7. Нейтральная линия. Опасные точки сечения.

Получим формулу для определения
положения нейтральной линии сечения.
Y
Предположим, что нейтральная линия
проходит через точки T(xN,0) u P(0,yN).
Тогда
X
T xN С
yN
σ Tz 0 ; σ Pz 0
Из (10.2)
F yF 0 x F x N
σ
1 2 2
0
A
ix
iy
T
z
Р
Н.л.
xF xN
1
0
2
i
y
xN
i2y
xF
;

8.

Аналогично из условия
σ 0
P
z
i2x
получим y N
yF
Таким образом, получены формулы для определения положения
нейтральной линии:
i2y
i
x N ; yN
xF
yF
2
x
(10.3)

9.

F yF y x F x
σz
1 2 2
A
ix
iy
Y
(10.2)
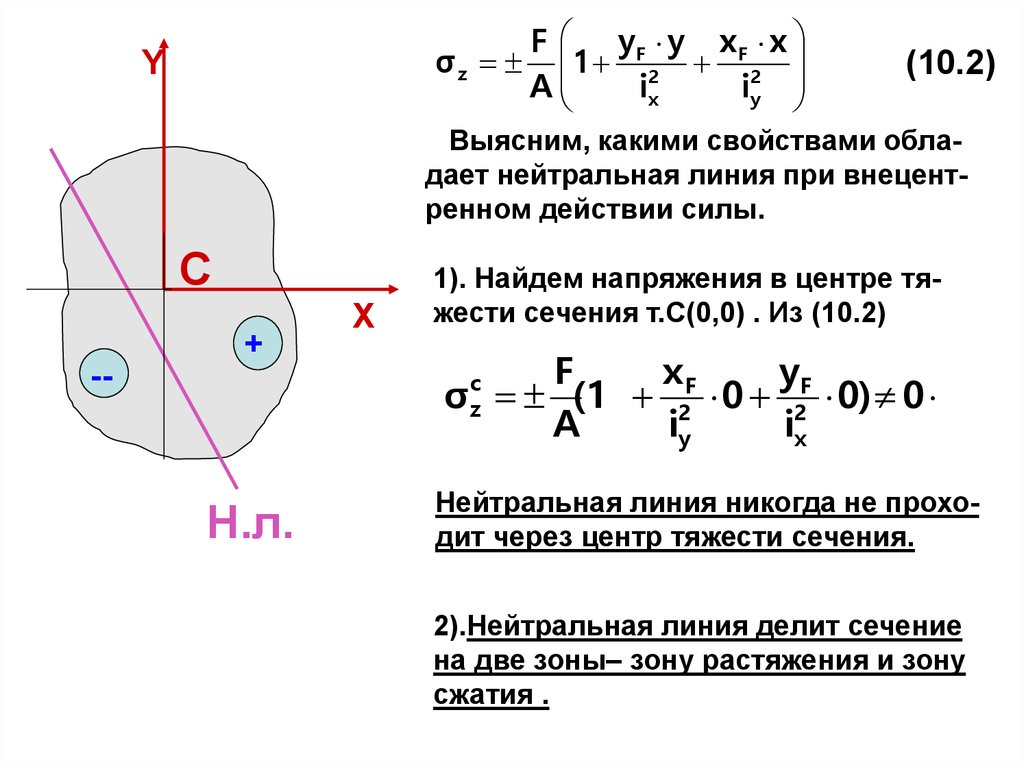
Выясним, какими свойствами обладает нейтральная линия при внецентренном действии силы.
С
+
--
X
1). Найдем напряжения в центре тяжести сечения т.С(0,0) . Из (10.2)
F
xF
yF
σ (1 2 0 2 0) 0
A
iy
ix
c
z
Н.л.
Нейтральная линия никогда не проходит через центр тяжести сечения.
2).Нейтральная линия делит сечение
на две зоны– зону растяжения и зону
сжатия .

10.

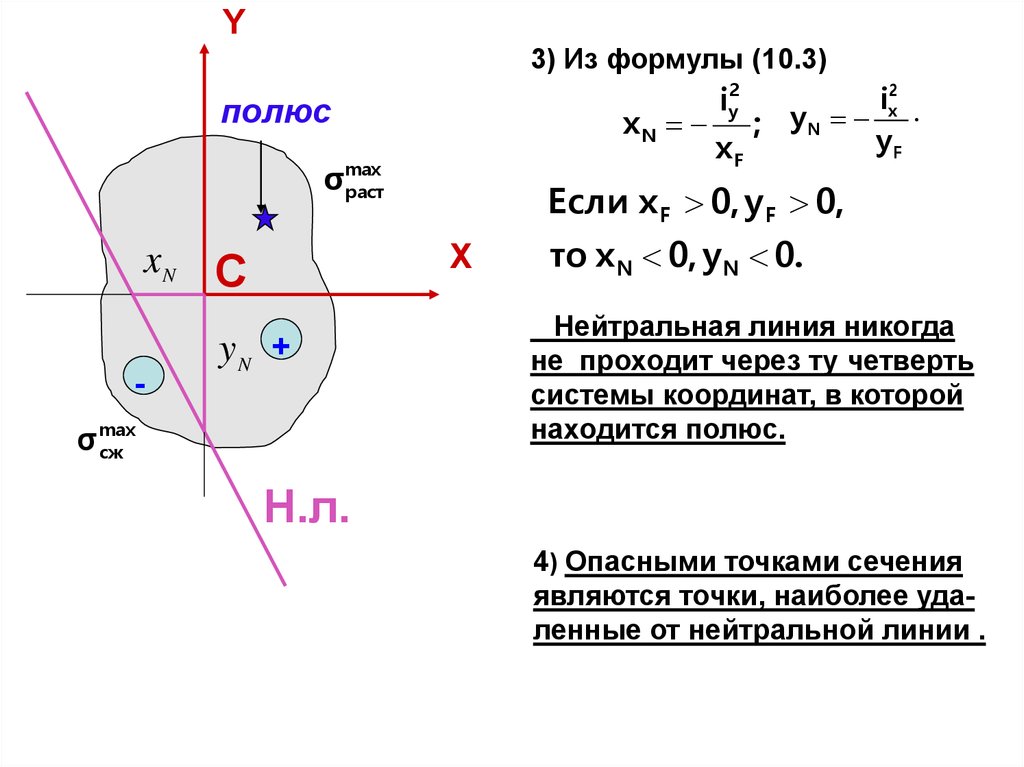
Y
3) Из формулы (10.3)
i2y
i2x
x N ; yN
yF
xF
полюс
σ max
раст
X
xN С
-
yN
Если x F 0, yF 0,
+
σ max
сж
то x N 0, yN 0.
Нейтральная линия никогда
не проходит через ту четверть
системы координат, в которой
находится полюс.
Н.л.
4) Опасными точками сечения
являются точки, наиболее удаленные от нейтральной линии .

11.

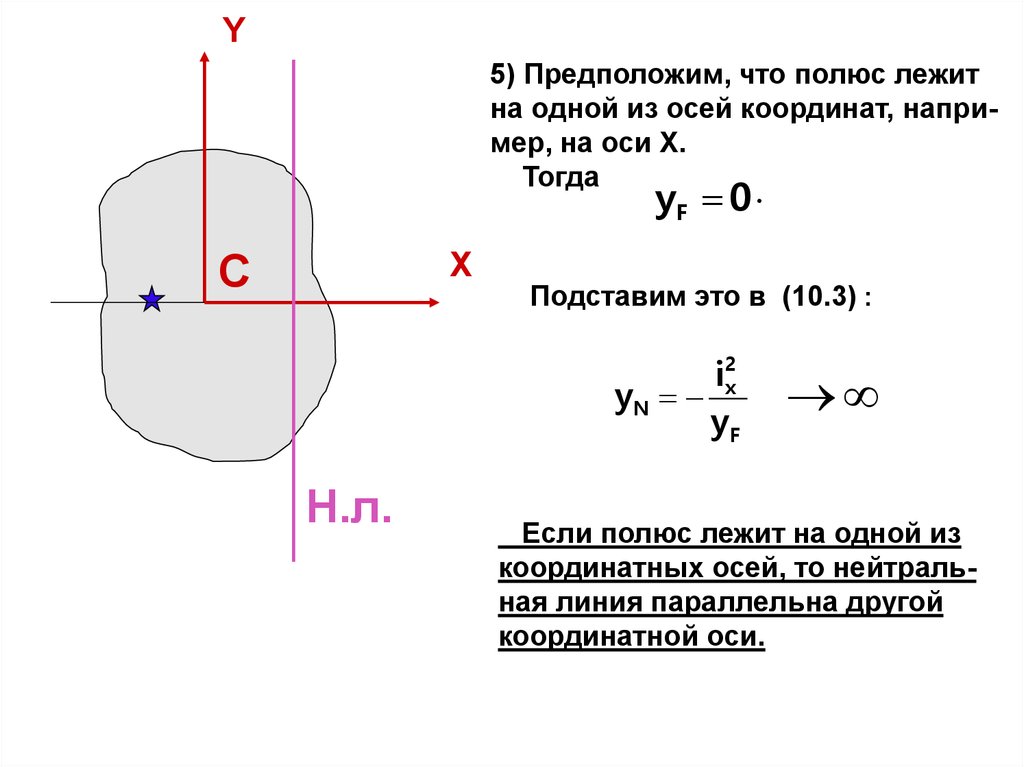
Y
5) Предположим, что полюс лежит
на одной из осей координат, например, на оси Х.
Тогда
yF 0
С
X
Подставим это в (10.3) :
i2x
yN
yF
Н.л.
Если полюс лежит на одной из
координатных осей, то нейтральная линия параллельна другой
координатной оси.

12. Ядро сечения

Y
F
X
σz
Осевое сжатие
Внецентренное действие
силы часто возникает в
стойках, колоннах,
выполненных из хрупких
материалов– бетон, камень,
кирпич, которые хорошо
работают на сжатие и плохо –
на растяжение. Поэтому
проектируют такие конструкции таким образом, чтобы
в них вообще не возникали
растягивающие напряжения.
Это возможно, если сжимающая сила приложена к стойке
центрально ,

13.

Y
F
Ядро
сечения
X
σz
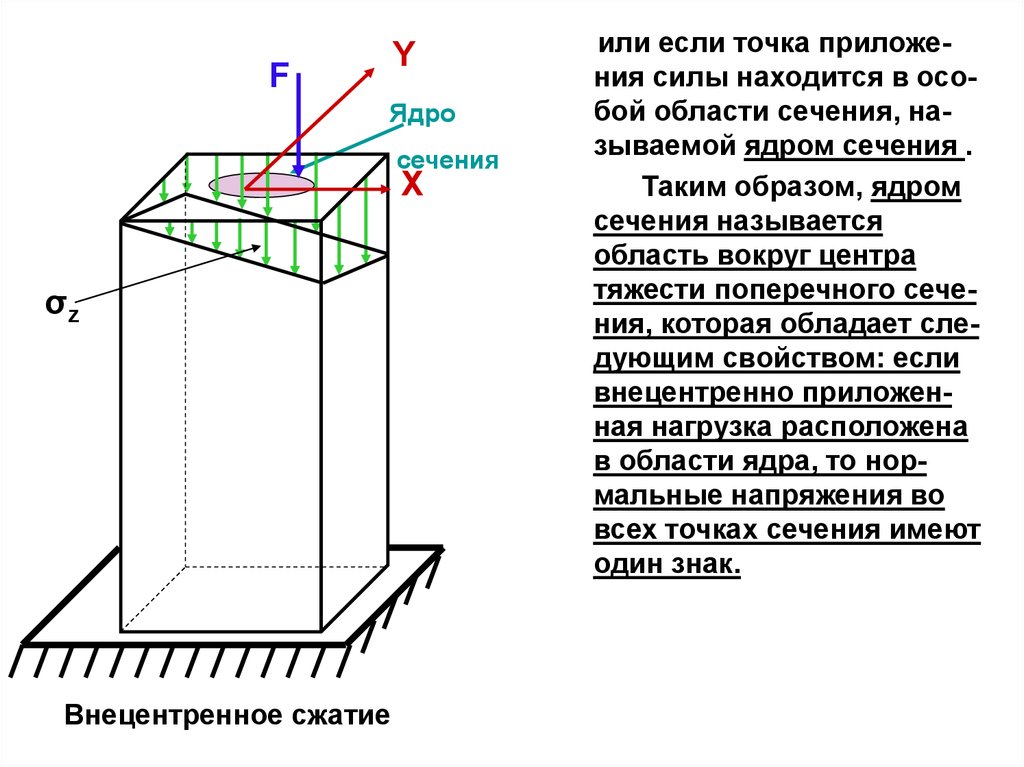
Внецентренное сжатие
или если точка приложения силы находится в особой области сечения, называемой ядром сечения .
Таким образом, ядром
сечения называется
область вокруг центра
тяжести поперечного сечения, которая обладает следующим свойством: если
внецентренно приложенная нагрузка расположена
в области ядра, то нормальные напряжения во
всех точках сечения имеют
один знак.

14.

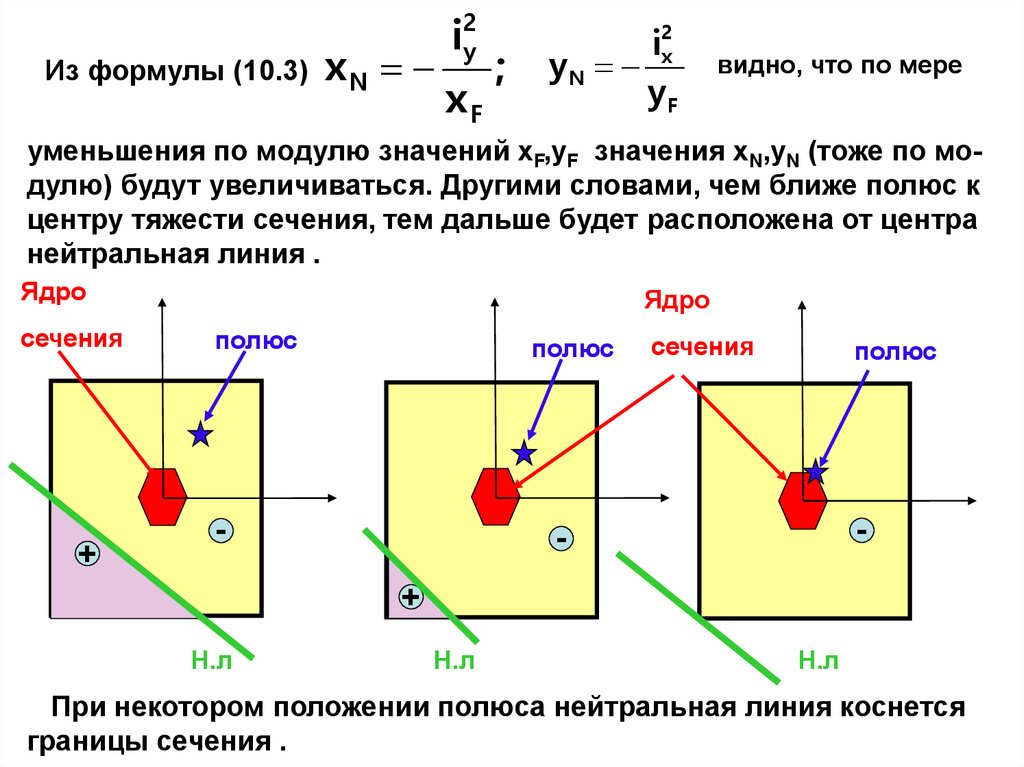
Из формулы (10.3)
xN
i
2
y
xF
;
i2x
yN
yF
видно, что по мере
уменьшения по модулю значений xF,yF значения xN,yN (тоже по модулю) будут увеличиваться. Другими словами, чем ближе полюс к
центру тяжести сечения, тем дальше будет расположена от центра
нейтральная линия .
Ядро
сечения
+
Ядро
полюс
полюс
-
сечения
полюс
-
+
Н.л
Н.л
Н.л
При некотором положении полюса нейтральная линия коснется
границы сечения .

15.

Н.Л.
F
F
Ядро
сечения
Н.Л.

16.

Y
1
У1
X
h
А
В
b
Это обстоятельство можно использовать при определении положения ядра
сечения. Рассмотрим, например, прямоугольное сечение .
Предположим, что полюс
расположен в точке 1 и что
эта точка находится на границе ядра сечения.
Найдем координату У1
этой точки. Если точка 1 –
точка границы ядра, то
нейтральная линия будет
касаться противоположной
стороны сечения, то есть
занимать положение линии
АВ.
Нормальное напряжение
в любой точке этой линии,
например, в т.А, будет
равно нулю.

17.

b h
В т.А , σ z 0.
2 2
Y
Из (10.2) :
1
h
X
2
4
3
А
h
F y1 2
0
1
0
A
i2x
Отсюда
В
b
F y1 y A x1 x A
σ
1 2 2
A
ix
iy
A
z
У1
i2x
y1
.
h
2
Аналогично можно найти координаты еще трех точек 2,3,4 границы ядра сечения. .

18.

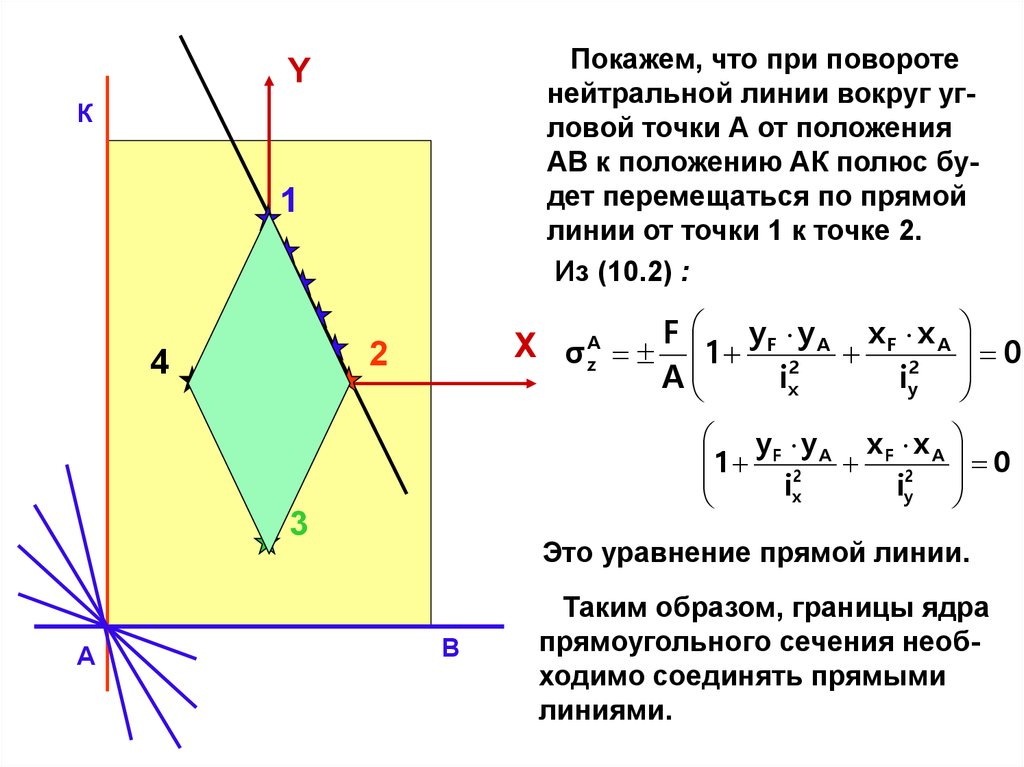
Покажем, что при повороте
нейтральной линии вокруг угловой точки А от положения
АВ к положению АК полюс будет перемещаться по прямой
линии от точки 1 к точке 2.
Из (10.2) :
Y
К
1
2
4
A
ix
iy
yF y A x F x A
1
0
2
2
ix
iy
3
А
X σ zA F 1 yF 2y A x F 2x A 0
Это уравнение прямой линии.
В
Таким образом, границы ядра
прямоугольного сечения необходимо соединять прямыми
линиями.

19.

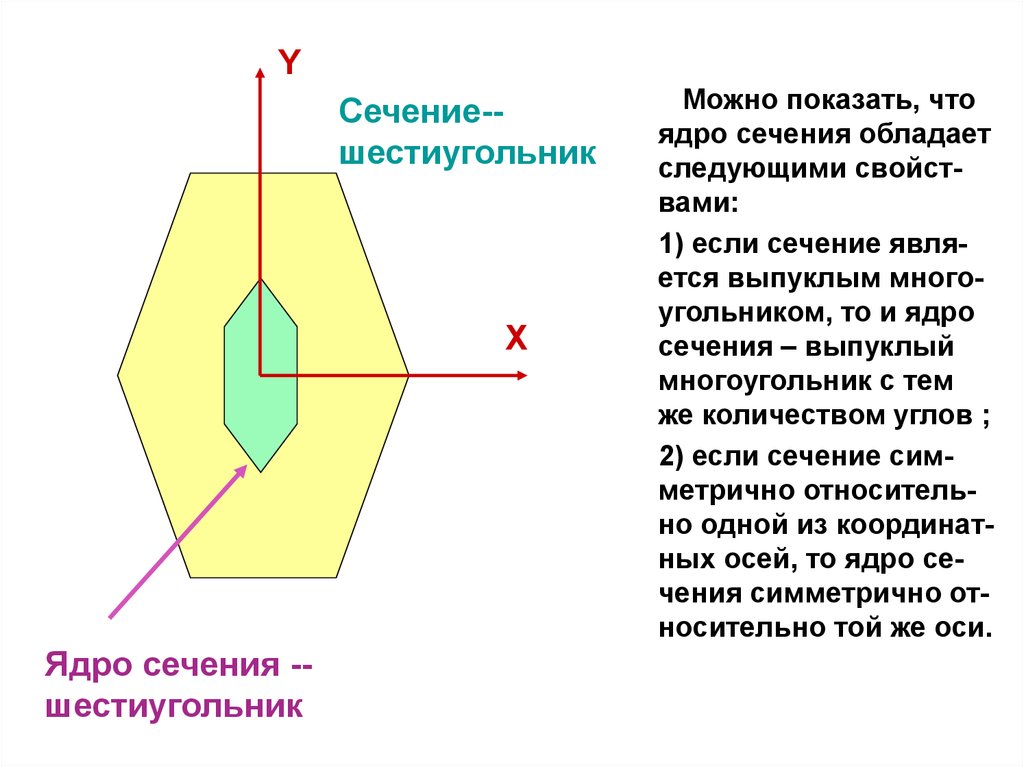
Y
Сечение-шестиугольник
X
Ядро сечения -шестиугольник
Можно показать, что
ядро сечения обладает
следующими свойствами:
1) если сечение является выпуклым многоугольником, то и ядро
сечения – выпуклый
многоугольник с тем
же количеством углов ;
2) если сечение симметрично относительно одной из координатных осей, то ядро сечения симметрично относительно той же оси.