Similar presentations:
Расстояние от точки до плоскости
1. Расстояние от точки до плоскости.
2. Теоретический опрос.
- Угол между прямыми равен 900. Как называютсятакие прямые?
- Верно ли утверждение: «Прямая называется
перпендикулярной плоскости, если она
перпендикулярна некоторой прямой, лежащей в
этой плоскости?»
- Продолжите предложение: «Прямая
перпендикулярна плоскости, если она …»
- Что можно сказать о двух (3-х, 4-х) прямых,
перпендикулярных к одной плоскости?
- Две прямые, перпендикулярны третьей прямой, …
3. Теоретический опрос.
- Как определяется расстояние от точки до прямойна плоскости?
- Вспомним, как называются отрезки AM - ? AH - ?
Точка M? Точка H?
A
АМ – наклонная к прямой а
АН – перпендикуляр, проведенный из точки А к прямой а
Н – основание перпендикуляра
М – основание наклонной.
a
M
H
- А как же определить расстояние от точки до
плоскости?
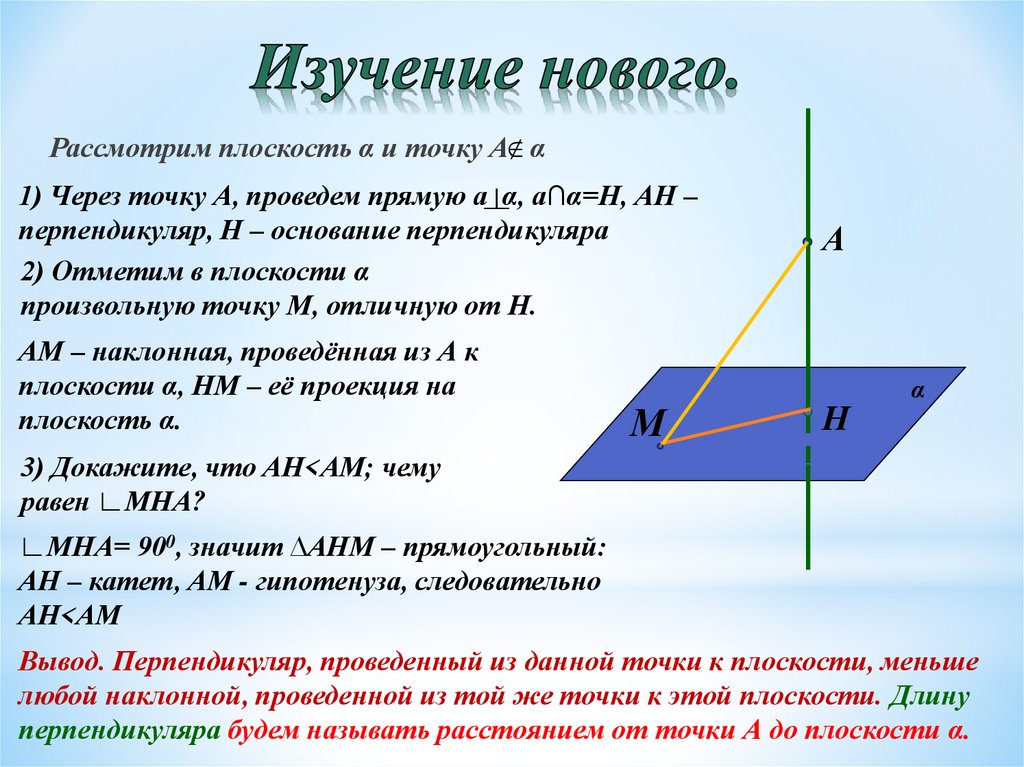
4. Изучение нового.
Рассмотрим плоскость α и точку А α1) Через точку А, проведем прямую а α, а∩α=Н, АН –
перпендикуляр, Н – основание перпендикуляра
2) Отметим в плоскости α
произвольную точку М, отличную от Н.
АМ – наклонная, проведённая из А к
плоскости α, НМ – её проекция на
плоскость α.
М
А
Н
α
3) Докажите, что АН<АМ; чему
равен ∟МНА?
∟МНА= 900, значит ∆АНМ – прямоугольный:
АН – катет, АМ - гипотенуза, следовательно
АН<АМ
Вывод. Перпендикуляр, проведенный из данной точки к плоскости, меньше
любой наклонной, проведенной из той же точки к этой плоскости. Длину
перпендикуляра будем называть расстоянием от точки А до плоскости α.
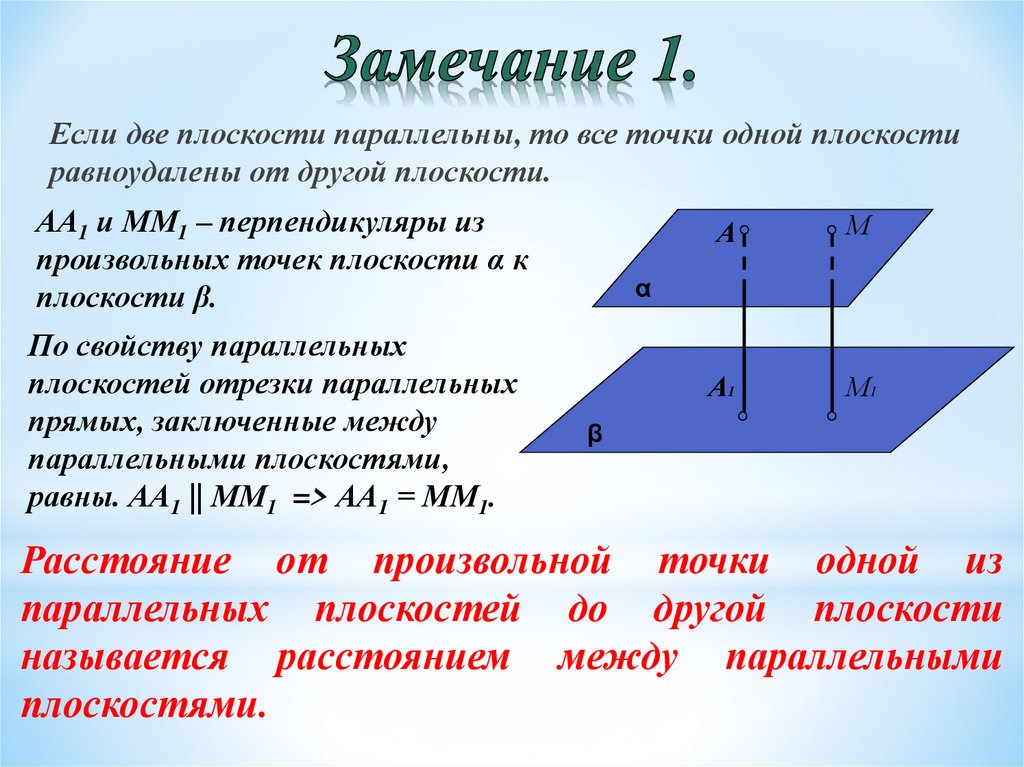
5. Замечание 1.
Если две плоскости параллельны, то все точки одной плоскостиравноудалены от другой плоскости.
АА1 и ММ1 – перпендикуляры из
произвольных точек плоскости α к
плоскости β.
По свойству параллельных
плоскостей отрезки параллельных
прямых, заключенные между
параллельными плоскостями,
равны. АА1 || ММ1 => АА1 = ММ1.
А
М
А1
М1
α
β
Расстояние от произвольной точки одной из
параллельных плоскостей до другой плоскости
называется расстоянием между параллельными
плоскостями.
6. Замечание 2.
Если прямая параллельна плоскости, то все точки прямойравноудалены от этой плоскости.
М
Доказательство приведено в задаче
№ 144
Изучить дома самостоятельно.
а
β
α
N
Расстояние от произвольной точки прямой до
плоскости называется расстоянием между прямой и
параллельной ей плоскостью.
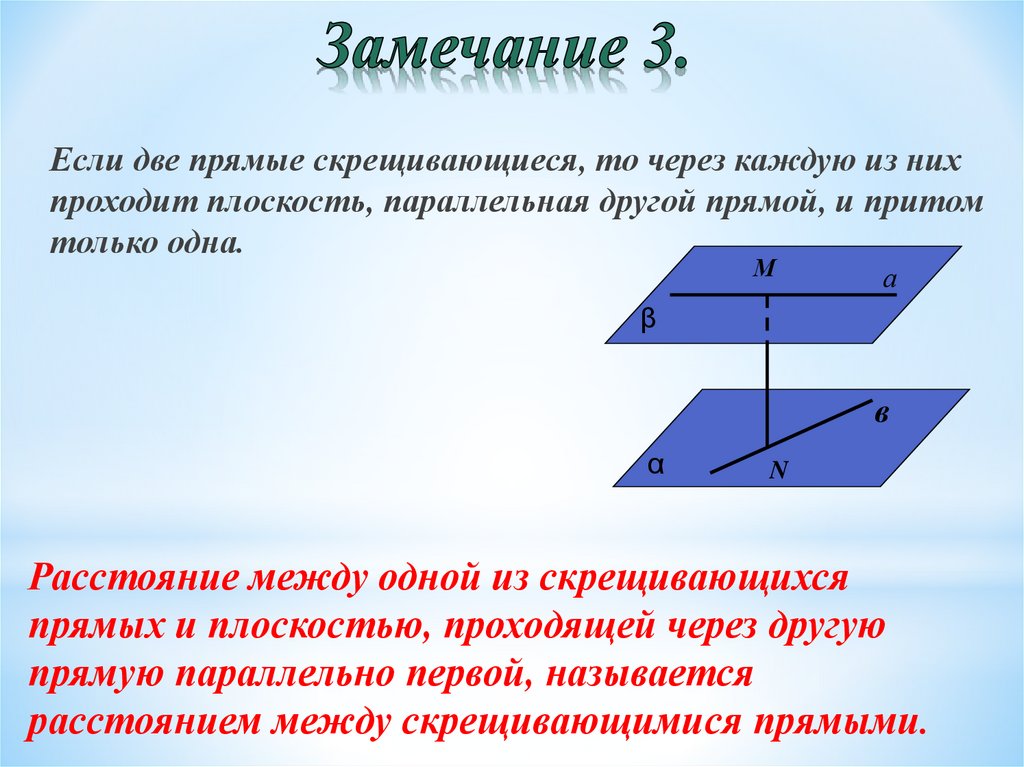
7. Замечание 3.
Если две прямые скрещивающиеся, то через каждую из нихпроходит плоскость, параллельная другой прямой, и притом
только одна.
М
а
β
в
α
N
Расстояние между одной из скрещивающихся
прямых и плоскостью, проходящей через другую
прямую параллельно первой, называется
расстоянием между скрещивающимися прямыми.
8. Решить задачи.
*№ 138 (а)*№ 139 (а)
*№ 140
*№ 143
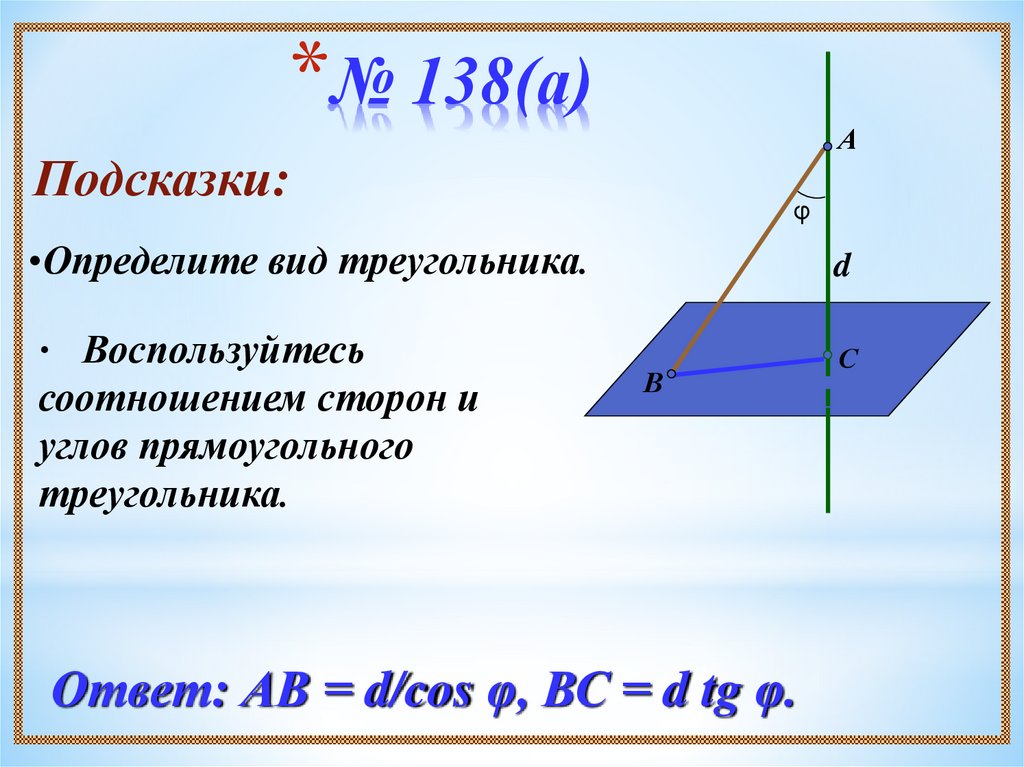
9. № 138(а)
*№ 138(а)А
Подсказки:
φ
•Определите вид треугольника.
d
• Воспользуйтесь
С
соотношением сторон и
углов прямоугольного
треугольника.
В
Ответ: АВ = d/cos φ, ВС = d tg φ.
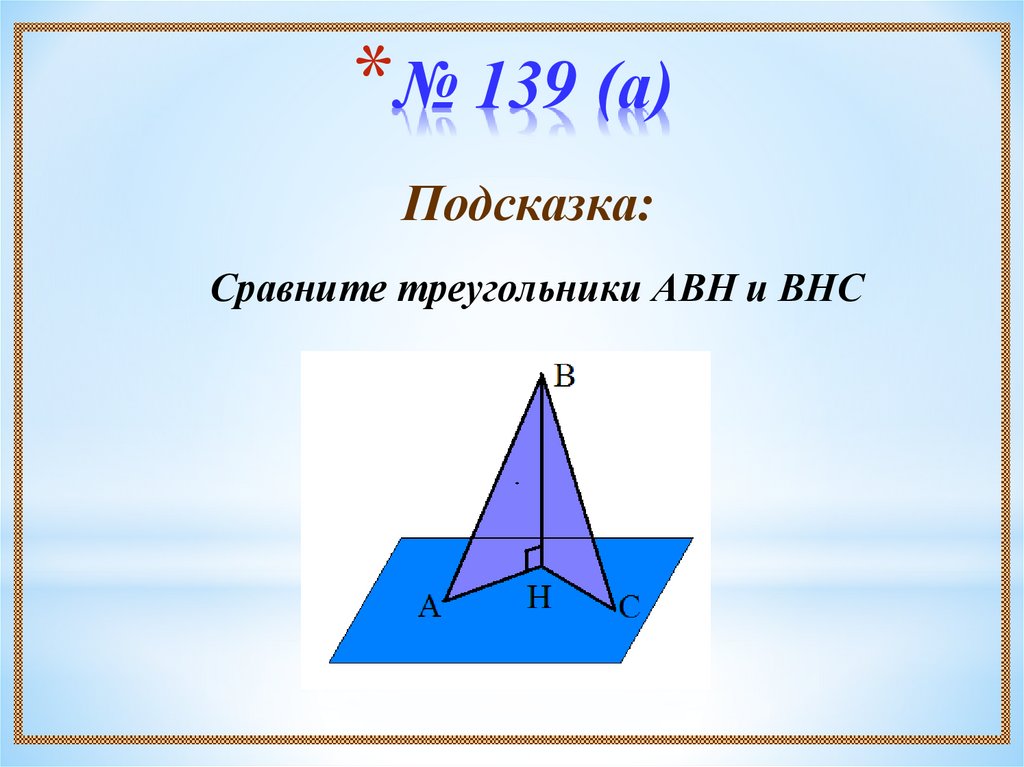
10. № 139 (а)
*№ 139 (а)Подсказка:
Сравните треугольники АВН и ВНС
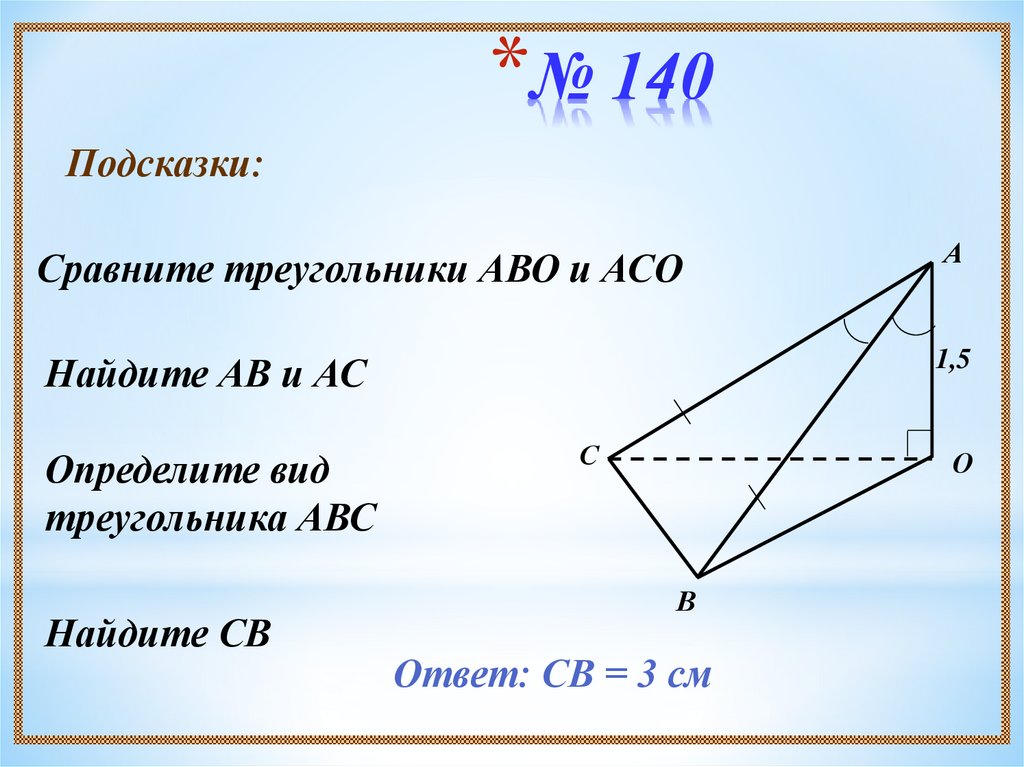
11. № 140
*№ 140Подсказки:
Сравните треугольники АВО и АСО
А
Найдите АВ и АС
1,5
Определите вид
треугольника АВС
Найдите СВ
С
О
В
Ответ: СВ = 3 см
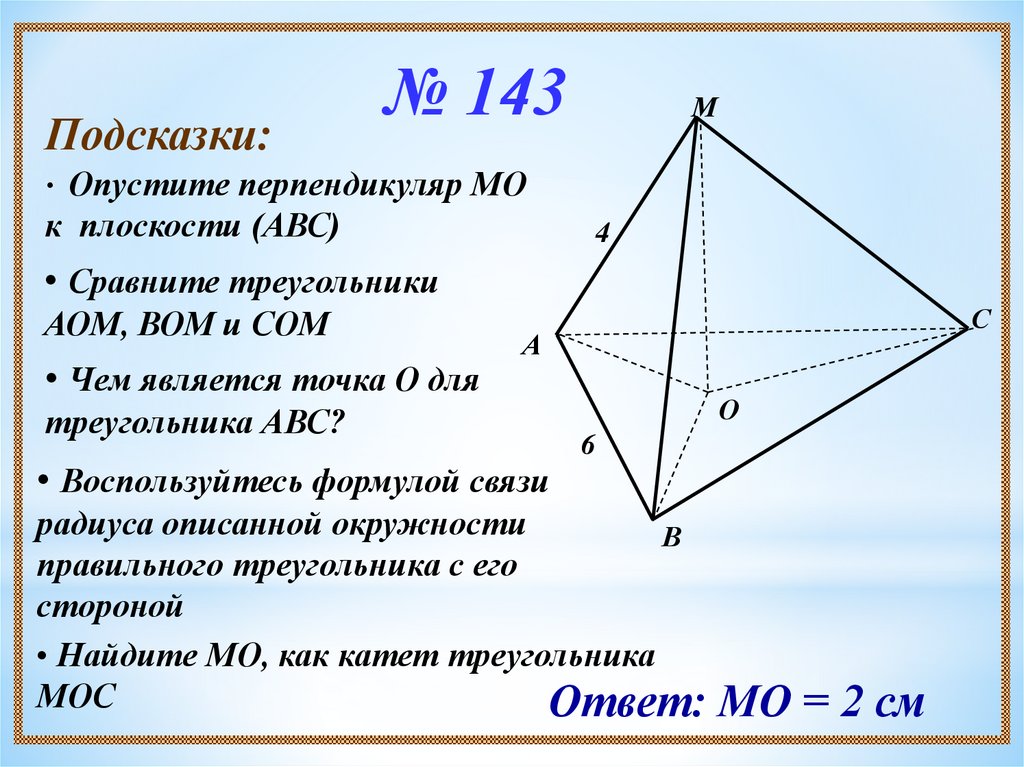
12.
Подсказки:№ 143
М
• Опустите перпендикуляр МО
к плоскости (АВС)
4
• Сравните треугольники
АОМ, ВОМ и СОМ
• Чем является точка О для
С
А
треугольника АВС?
• Воспользуйтесь формулой связи
О
6
радиуса описанной окружности
В
правильного треугольника с его
стороной
• Найдите МО, как катет треугольника
МОС
Ответ: МО = 2 см
13.
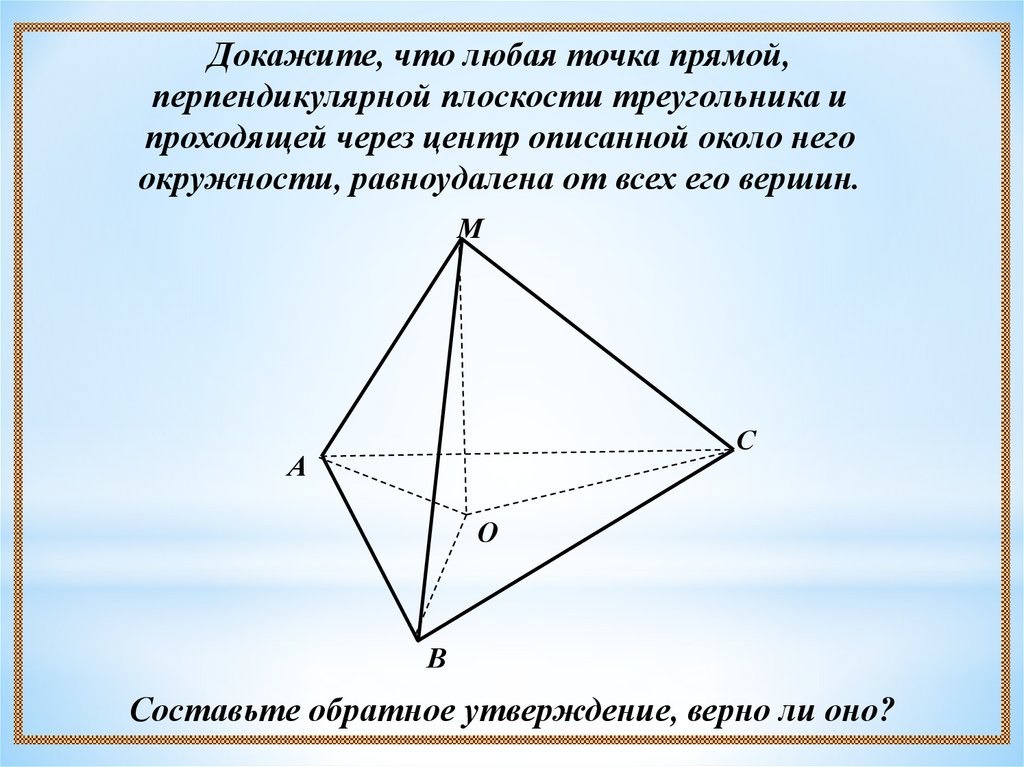
Какой вывод можно сделать из решения этой задачи?14.
Докажите, что любая точка прямой,перпендикулярной плоскости треугольника и
проходящей через центр описанной около него
окружности, равноудалена от всех его вершин.
М
С
А
О
В
Составьте обратное утверждение, верно ли оно?
15.
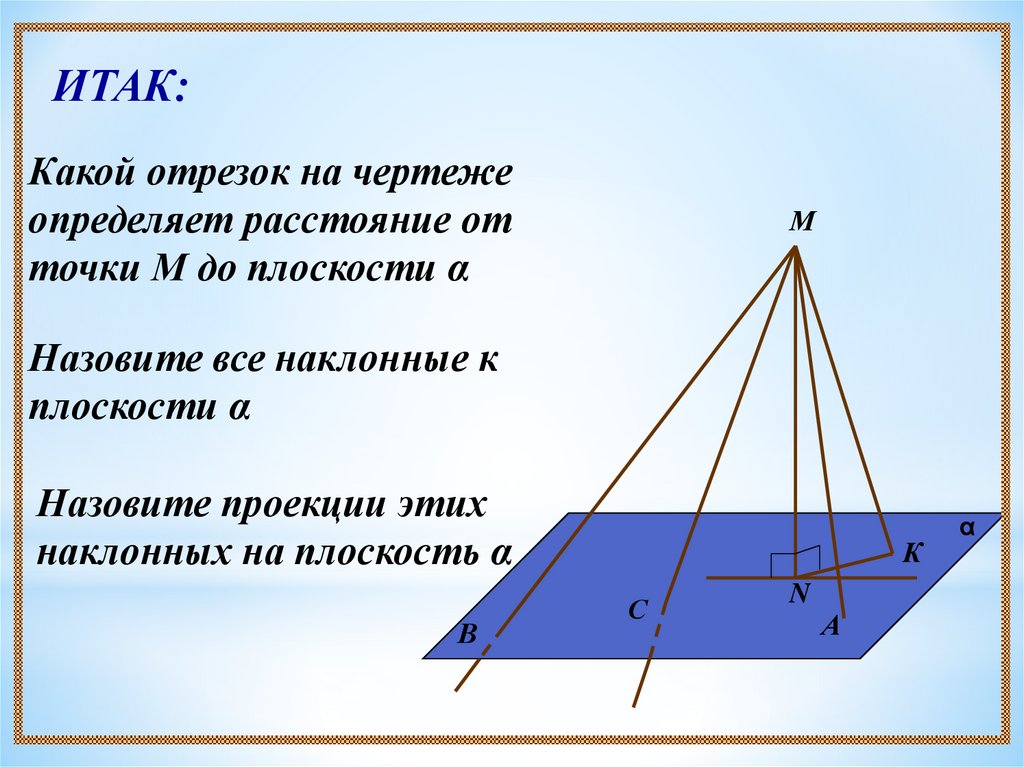
ИТАК:Какой отрезок на чертеже
определяет расстояние от
точки М до плоскости α
М
Назовите все наклонные к
плоскости α
Назовите проекции этих
наклонных на плоскость α
В
К
С
N
А
α
16.
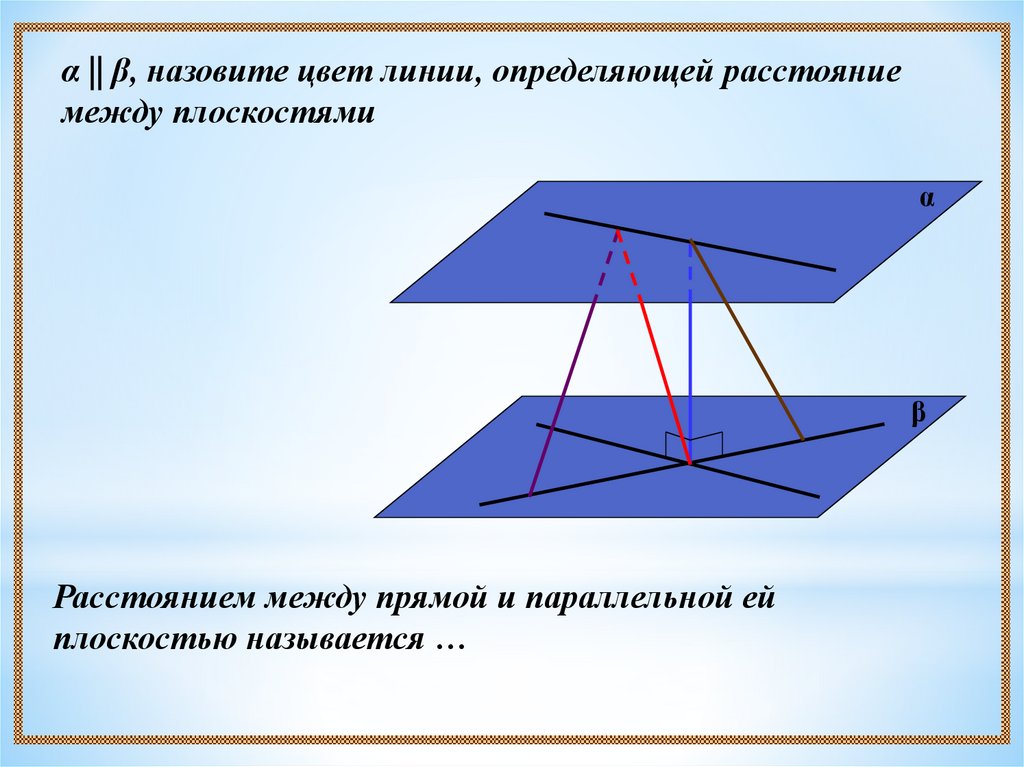
α || β, назовите цвет линии, определяющей расстояниемежду плоскостями
α
β
Расстоянием между прямой и параллельной ей
плоскостью называется …
17.
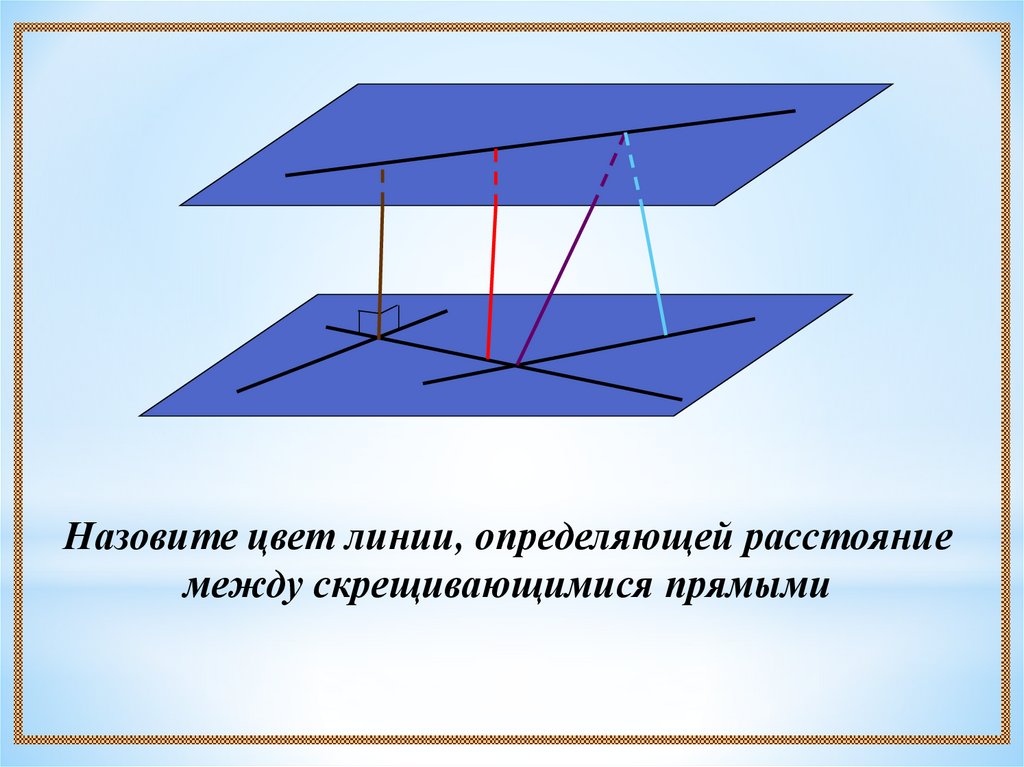
Назовите цвет линии, определяющей расстояниемежду скрещивающимися прямыми
18.
Домашнее заданиеТеория: пункт 19, стр. 40-41
Задачи: № 138 (б)
№ 141
№ 142
№ 144







 mathematics
mathematics








