Similar presentations:
Расстояние от точки до плоскости
1. Расстояние от точки до плоскости.
2.
Домашнее задание за 5.12.Теория: п.19, стр. 40-41, № 141, 142 + задача ЕГЭ:
3.
4. Теоретический опрос.
- Угол между прямыми равен 900. Как называются такиепрямые?
- Верно ли утверждение: «Прямая называется
перпендикулярной плоскости, если она перпендикулярна
некоторой прямой, лежащей в этой плоскости?»
- Продолжите предложение: «Прямая перпендикулярна
плоскости, если она …»
- Что можно сказать о двух (3-х, 4-х) прямых,
перпендикулярных к одной плоскости?
- Две прямые, перпендикулярны третьей прямой, …
5. Теоретический опрос.
- Как определяется расстояние от точки допрямой на плоскости?
- Вспомним, как называются отрезки AM - ? AH - ?
A
Точка M? Точка H?
АМ – наклонная к прямой а
АН – перпендикуляр, проведенный из точки А к прямой а
Н – основание перпендикуляра
М – основание наклонной.
M
H
- А как же определить расстояние от точки до
плоскости?
a
6.
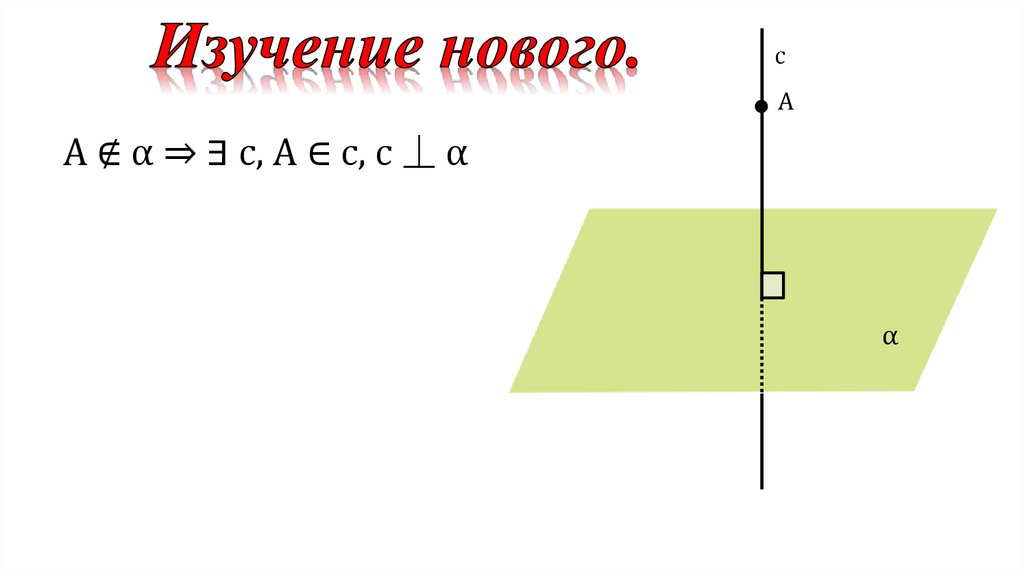
cA
A ∉ α ⇒ ∃ c, A ∈ c, c ⏊ α
α
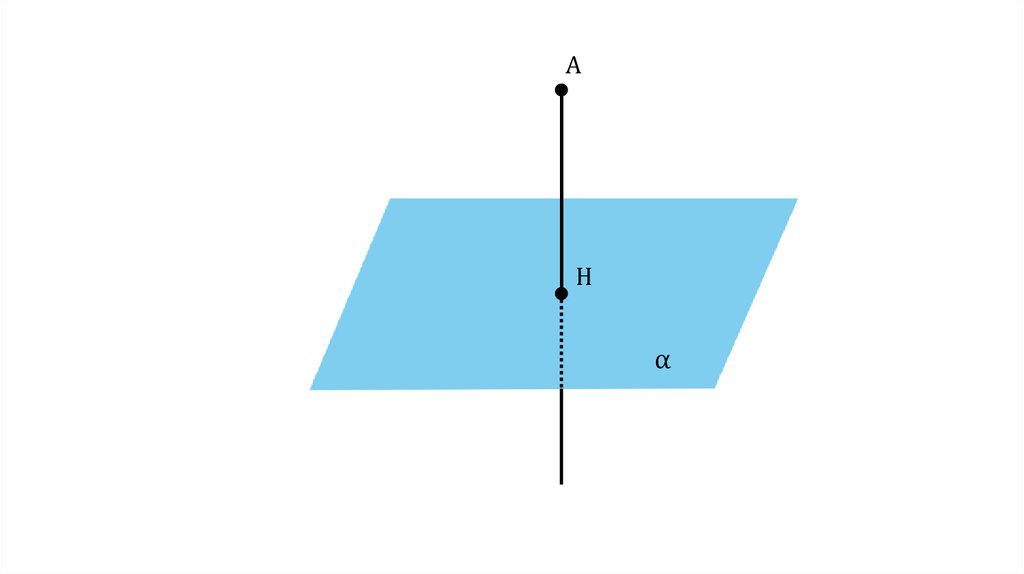
7.
Aα
8.
Aα
9.
AH
α
10.
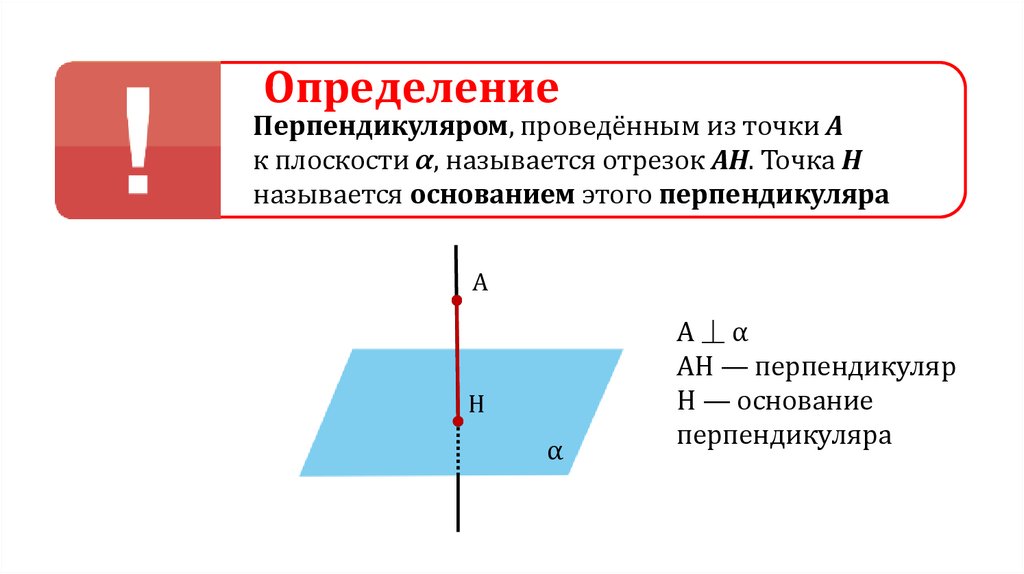
ОпределениеПерпендикуляром, проведённым из точки А
к плоскости α, называется отрезок АН. Точка Н
называется основанием этого перпендикуляра
A
H
α
A⏊α
AH — перпендикуляр
H — основание
перпендикуляра
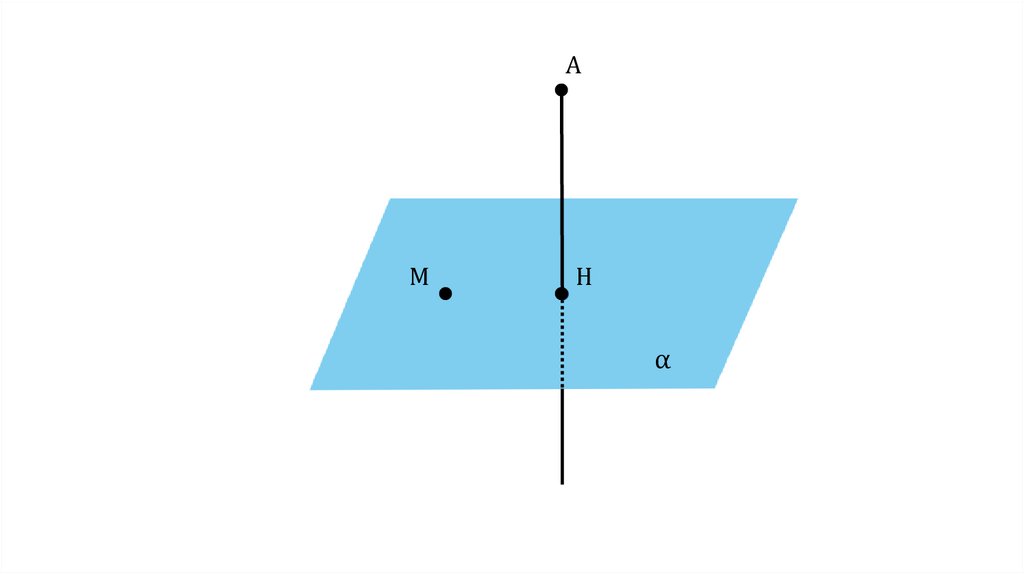
11.
AM
H
α
12.
AM
H
α
13.
AM
H
α
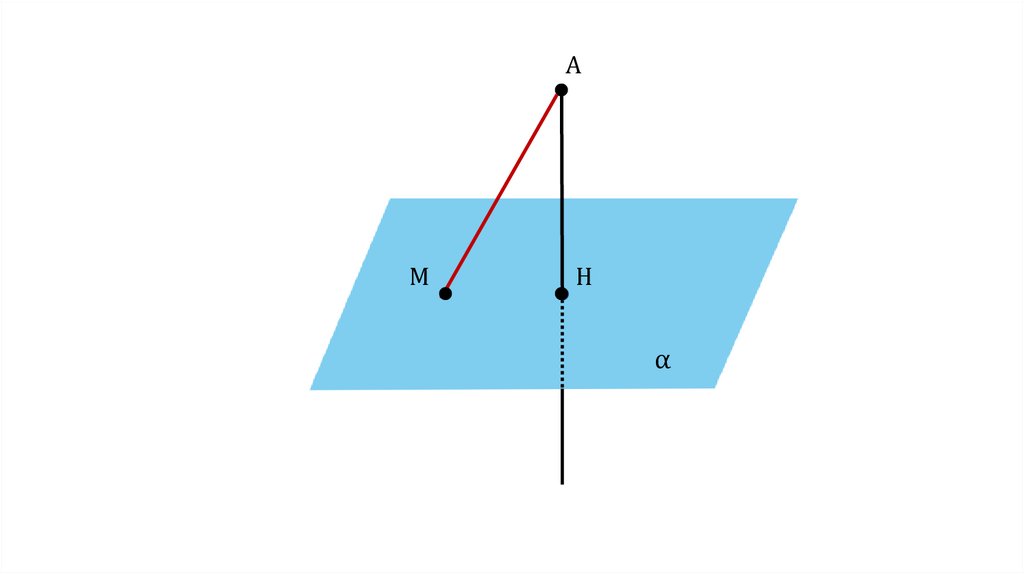
14.
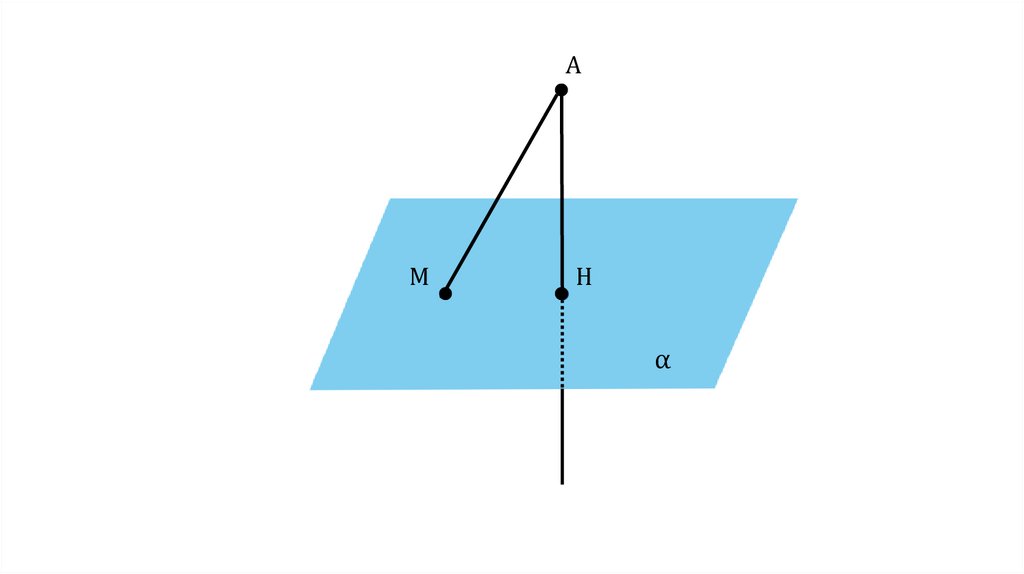
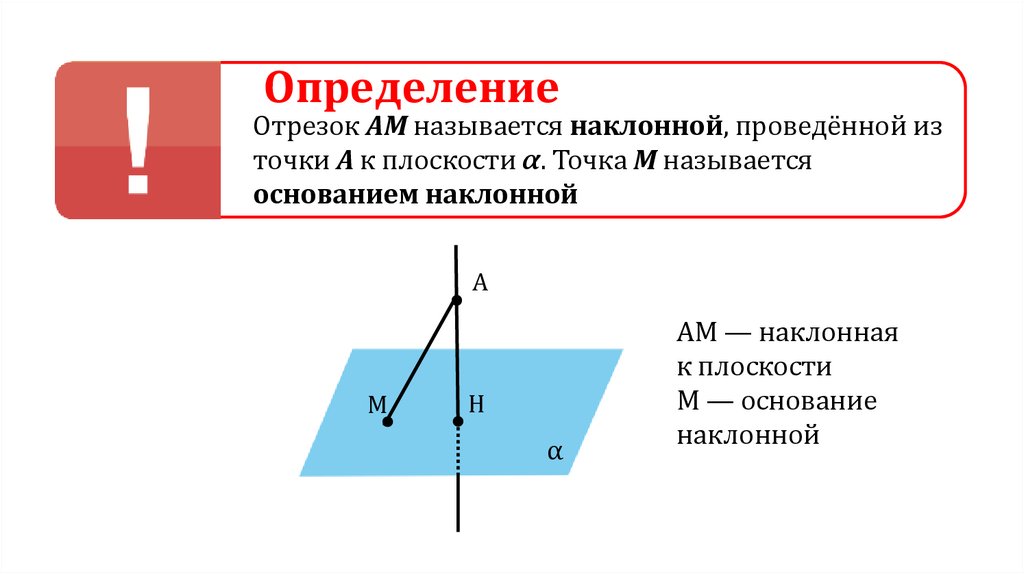
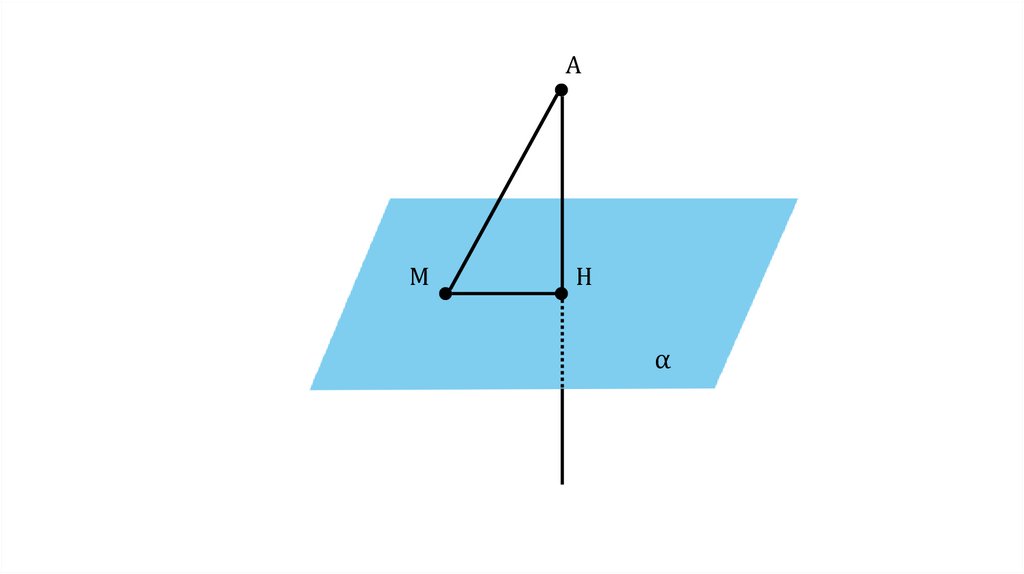
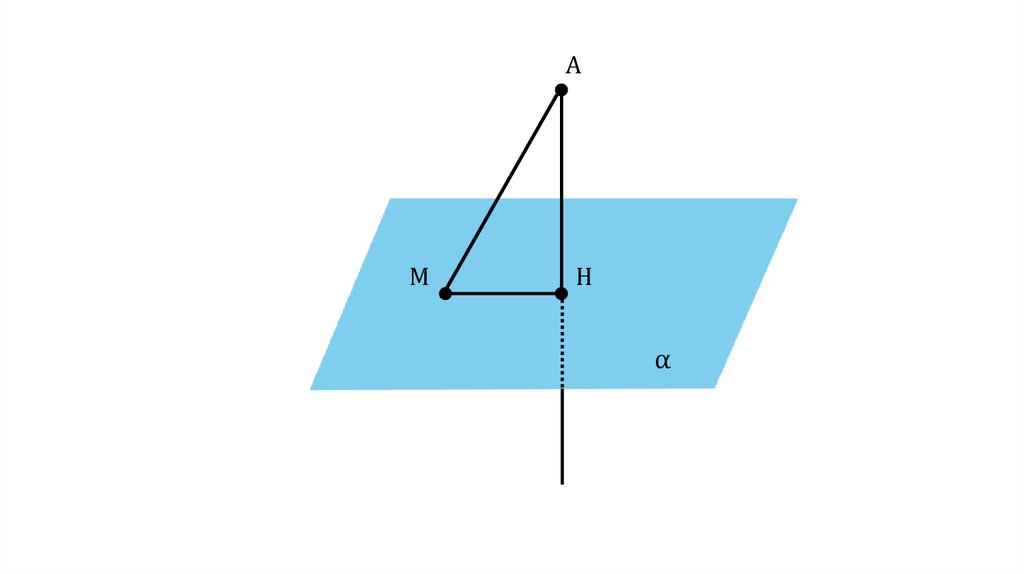
ОпределениеОтрезок АМ называется наклонной, проведённой из
точки А к плоскости α. Точка М называется
основанием наклонной
A
M
H
α
AM — наклонная
к плоскости
M — основание
наклонной
15.
AM
H
α
16.
AM
H
α
17.
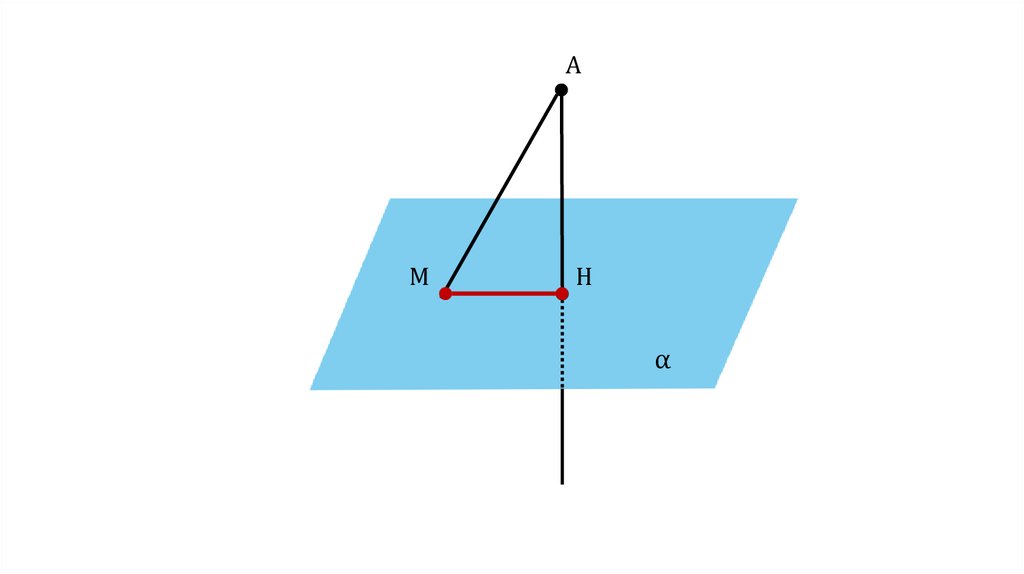
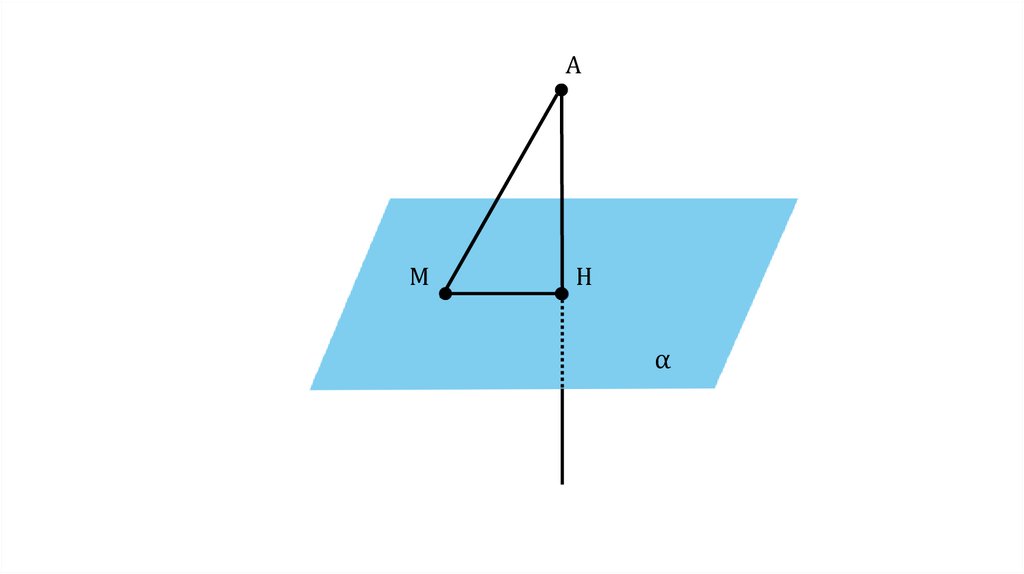
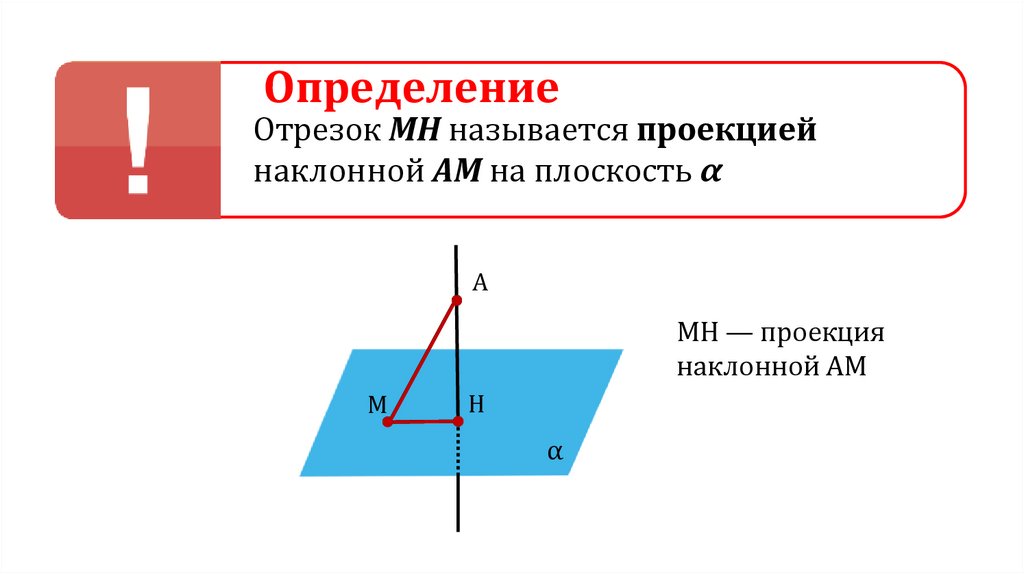
ОпределениеОтрезок МН называется проекцией
наклонной АМ на плоскость α
A
MH — проекция
наклонной AM
M
H
α
18.
AM
H
α
19.
AM
H
α
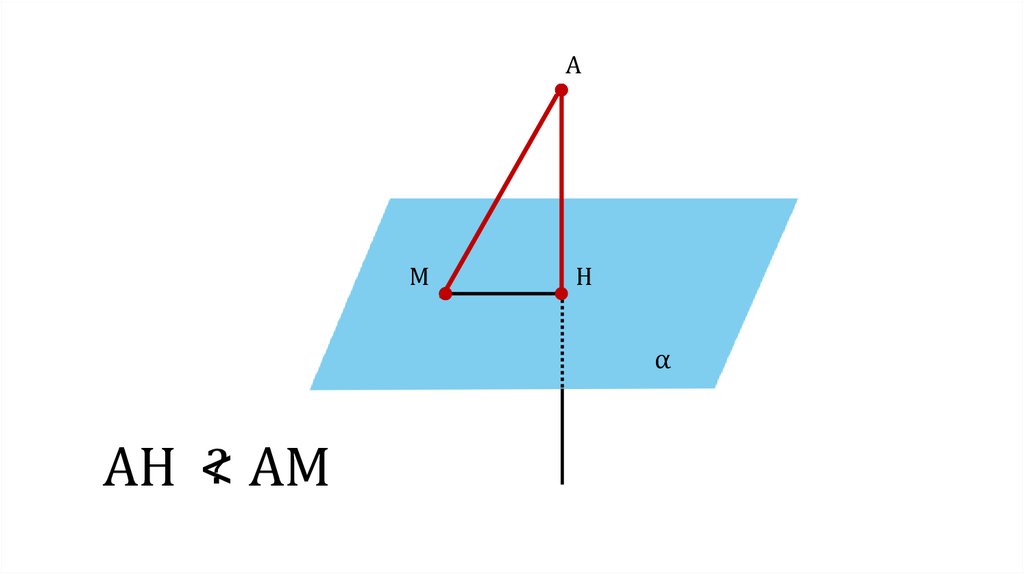
AH <? AM
20.
AM
H
α
21.
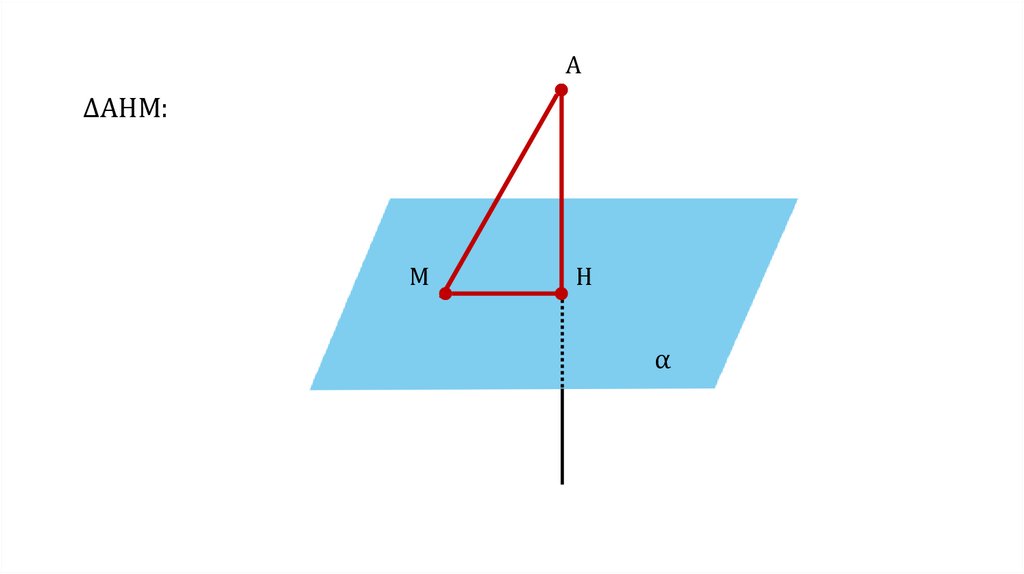
A∆AHM:
M
H
α
22.
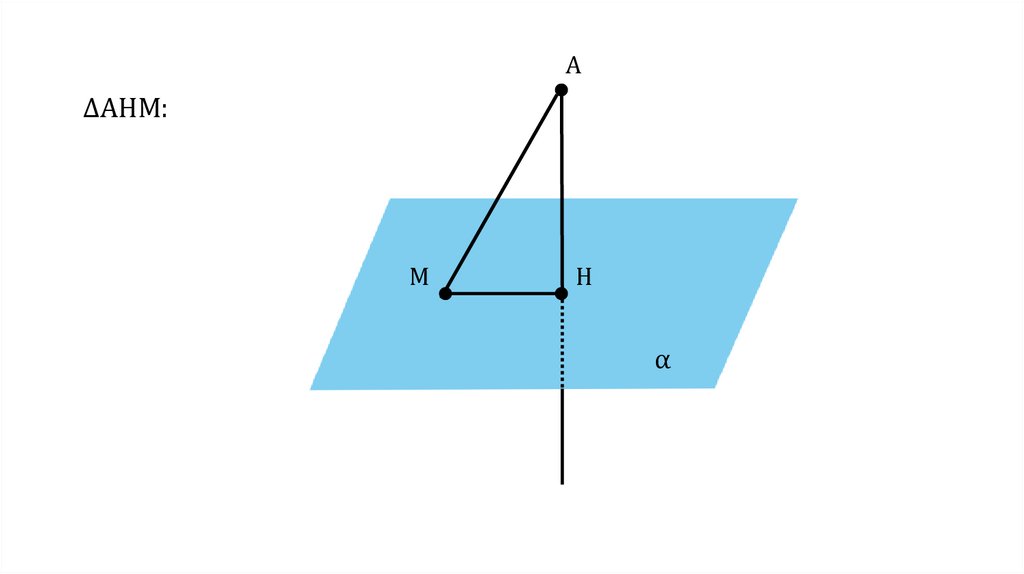
A∆AHM:
M
H
α
23.
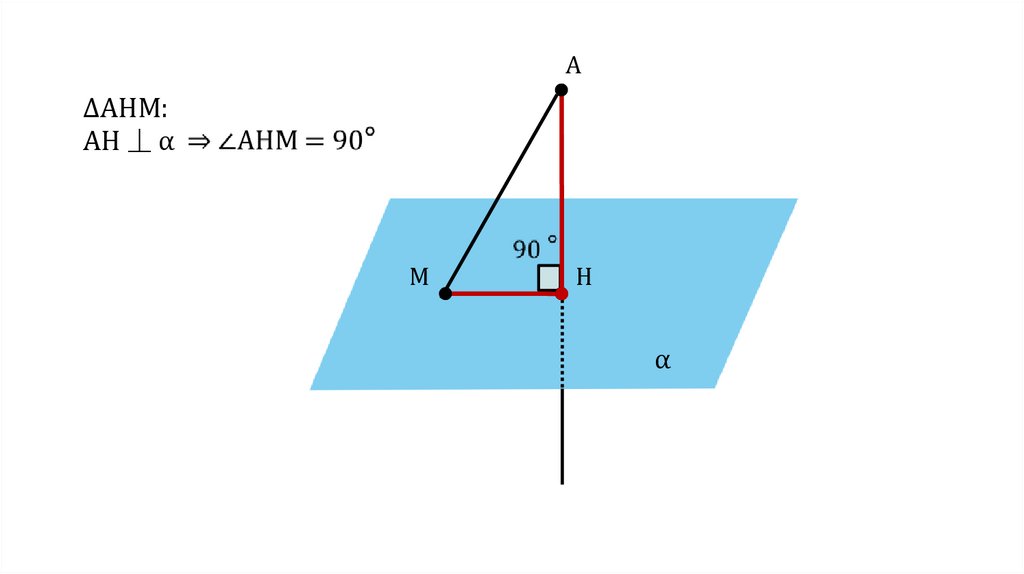
A∆AHM:
AH ⏊ α
M
H
α
24.
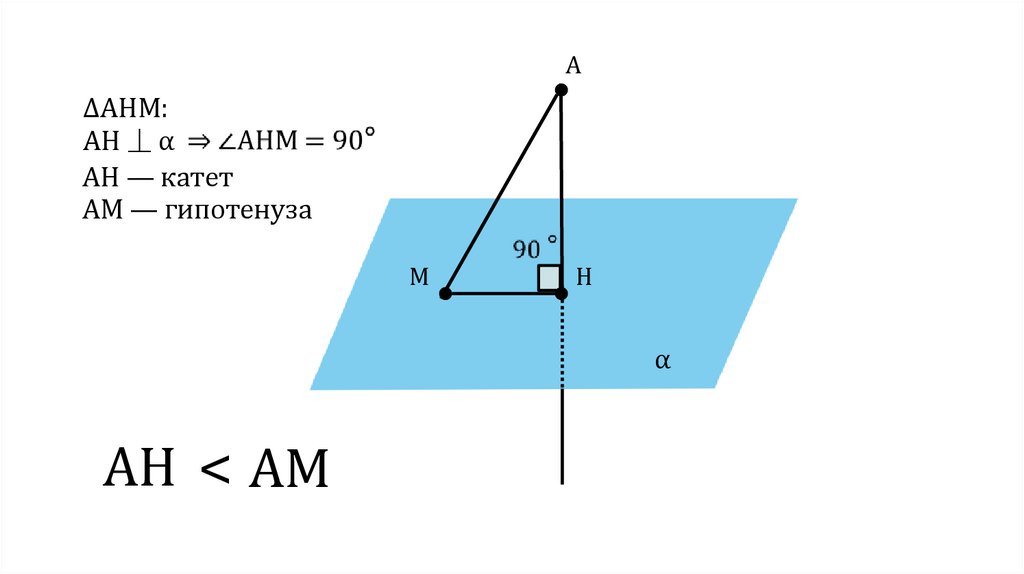
A∆AHM:
AH ⏊ α
АН — катет
АM — гипотенуза
M
H
α
AH < AM
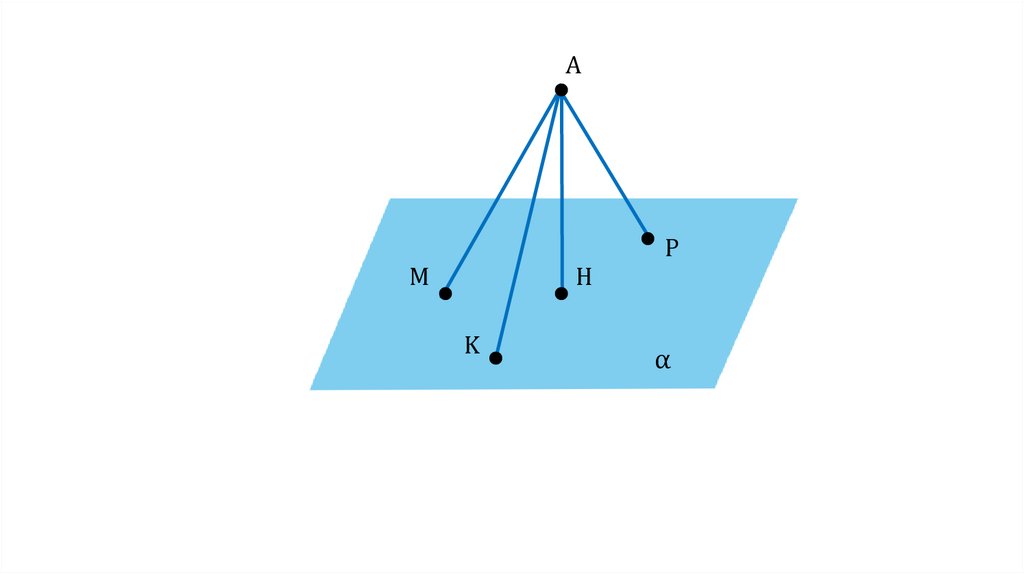
25.
AM
H
K
P
α
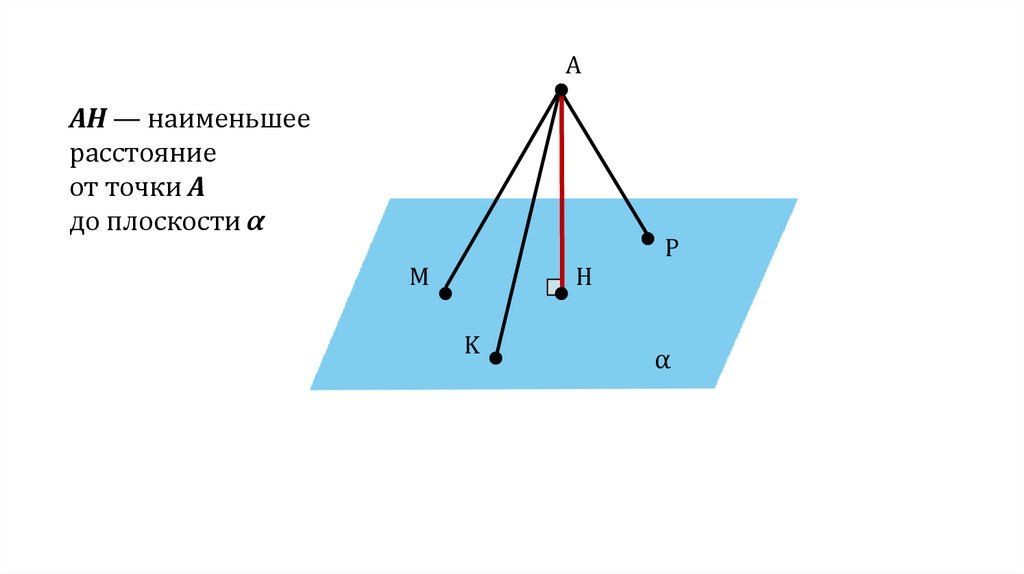
26.
AAH — наименьшее
расстояние
от точки A
до плоскости α
M
H
K
P
α
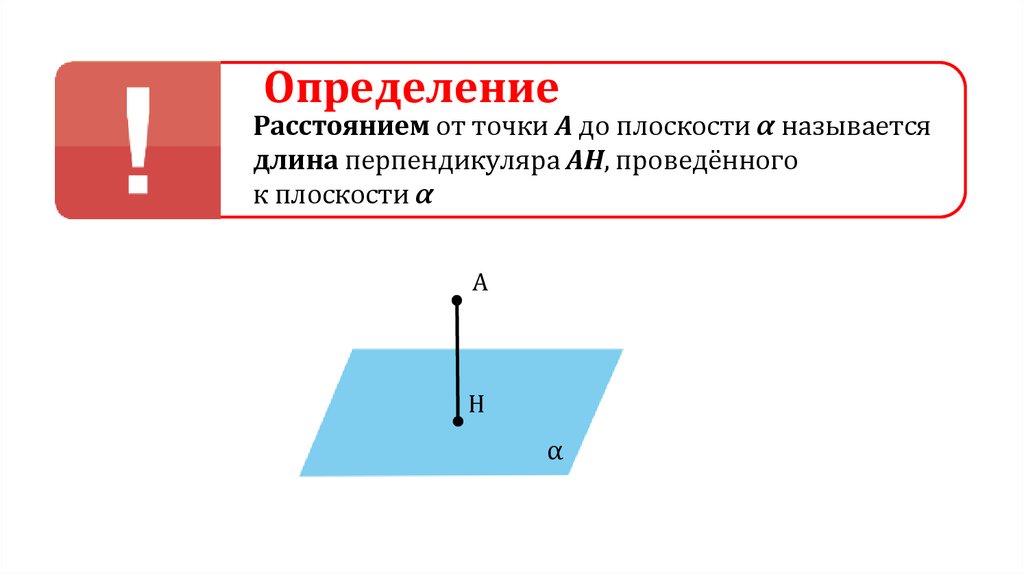
27.
ОпределениеРасстоянием от точки А до плоскости α называется
длина перпендикуляра АН, проведённого
к плоскости α
A
H
α
28.
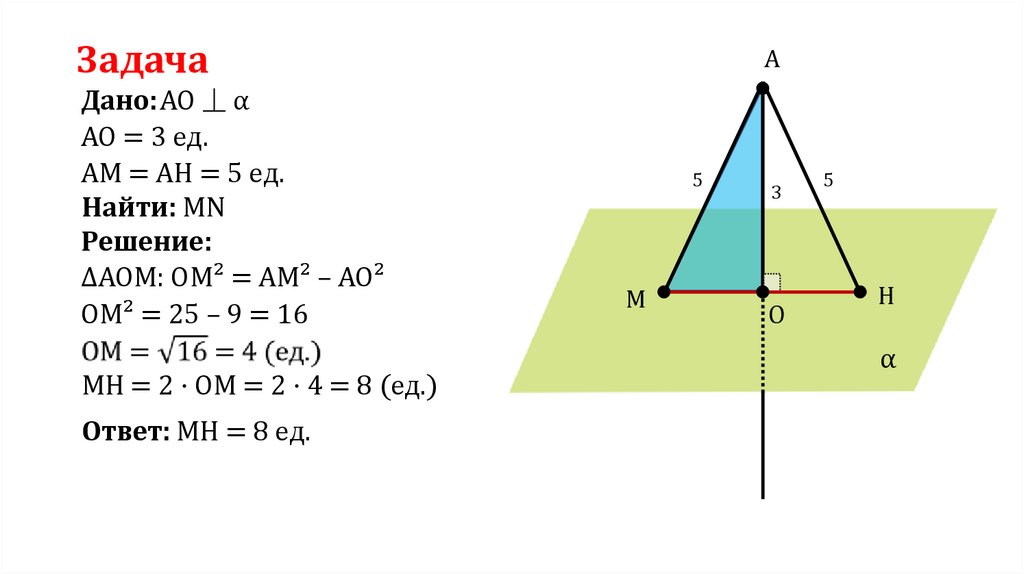
ЗадачаДано: AO ⏊ α
AO = 3 ед.
AM = АН = 5 ед.
Найти: MN
Решение:
∆АОМ: ОМ² = АМ² – АО²
ОМ² = 25 – 9 = 16
МН = 2 · ОМ = 2 · 4 = 8 (ед.)
Ответ: МН = 8 ед.
A
5
M
3
O
5
H
α
29.
Замечание 1Пусть даны две параллельные плоскости α и β. Тогда все
точки плоскости α будут равноудалены от плоскости β
A
M
α
AH ∥ MO
β
H
O
30.
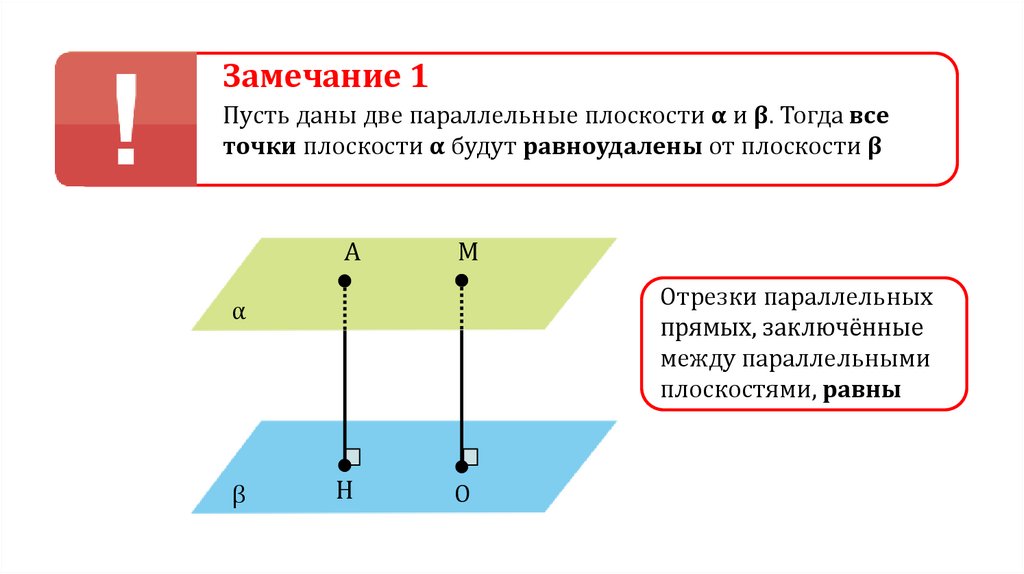
Замечание 1Пусть даны две параллельные плоскости α и β. Тогда все
точки плоскости α будут равноудалены от плоскости β
A
M
Отрезки параллельных
прямых, заключённые
между параллельными
плоскостями, равны
α
β
H
O
31.
ОпределениеРасстоянием между параллельными плоскостями называется
расстояние от произвольной точки одной из параллельных
плоскостей до другой
A
M
H
O
α
β
32.
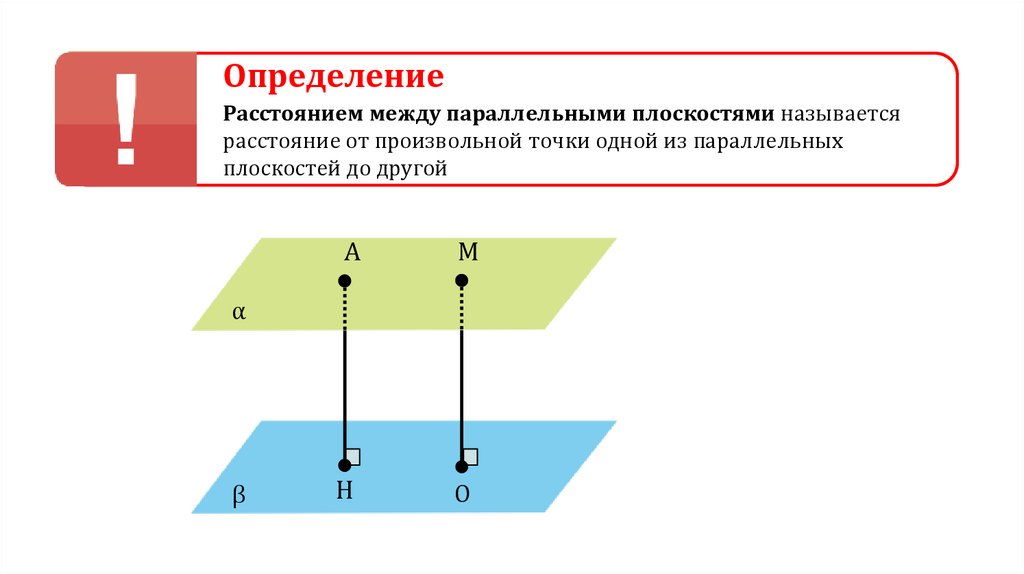
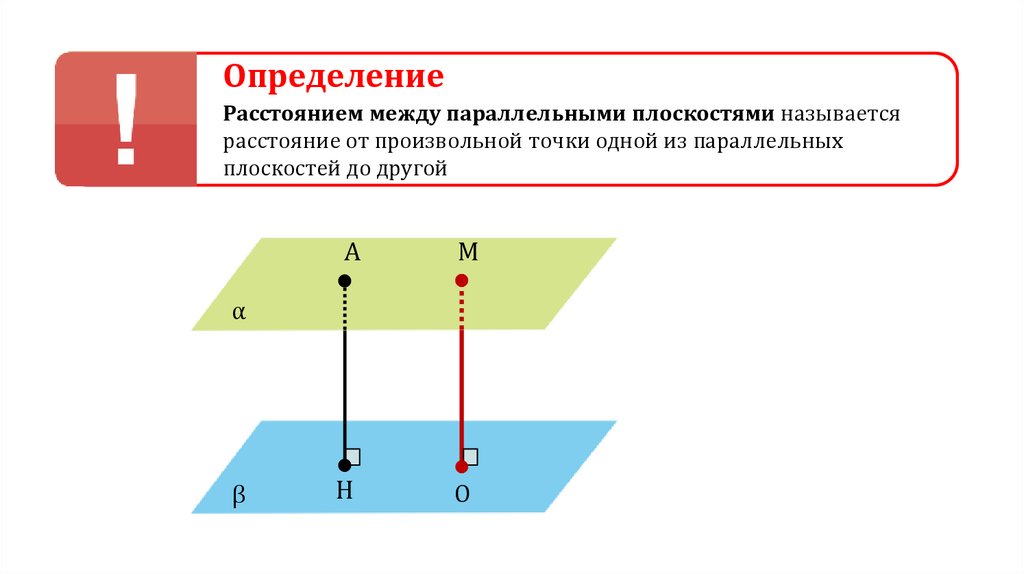
ОпределениеРасстоянием между параллельными плоскостями называется
расстояние от произвольной точки одной из параллельных
плоскостей до другой
A
M
H
O
α
β
33.
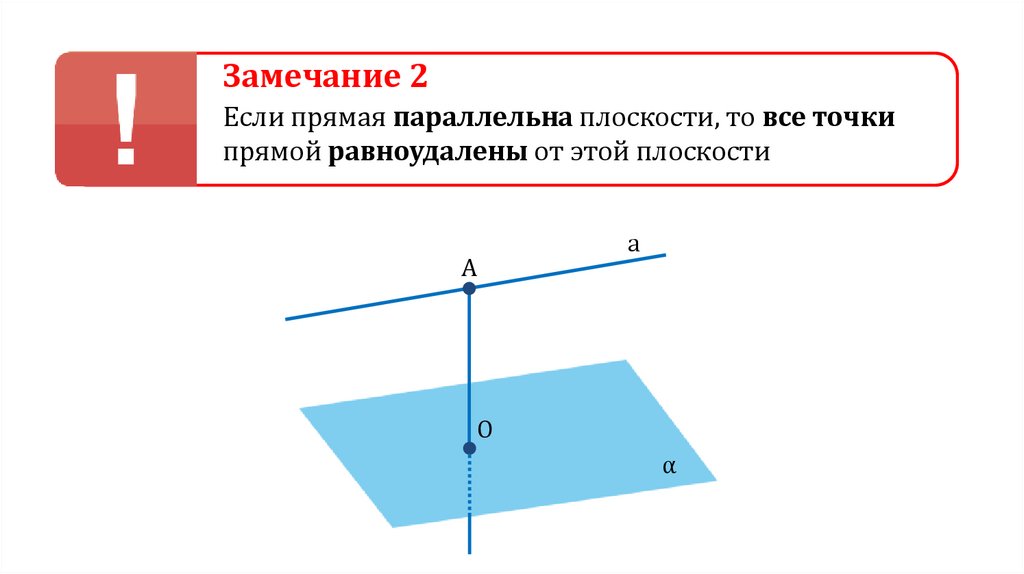
Замечание 2Если прямая параллельна плоскости, то все точки
прямой равноудалены от этой плоскости
a
A
O
α
34.
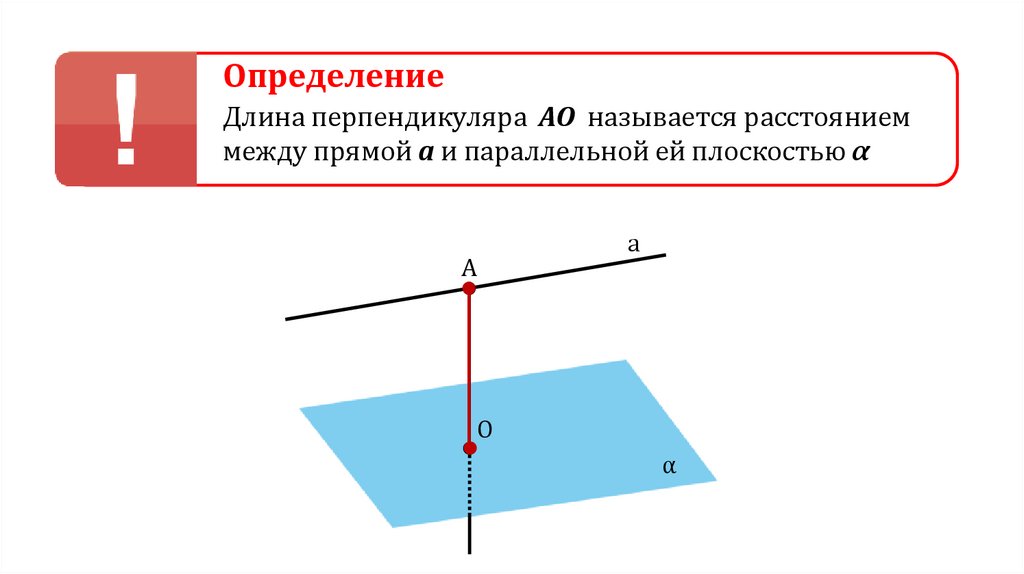
ОпределениеДлина перпендикуляра АО называется расстоянием
между прямой а и параллельной ей плоскостью α
a
A
O
α
35.
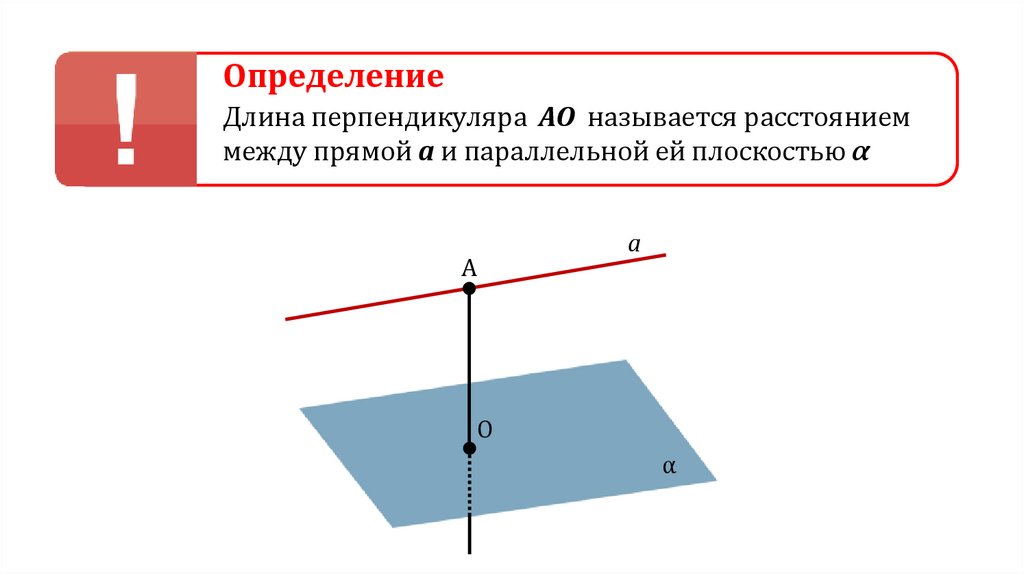
ОпределениеДлина перпендикуляра АО называется расстоянием
между прямой а и параллельной ей плоскостью α
a
A
O
α
36.
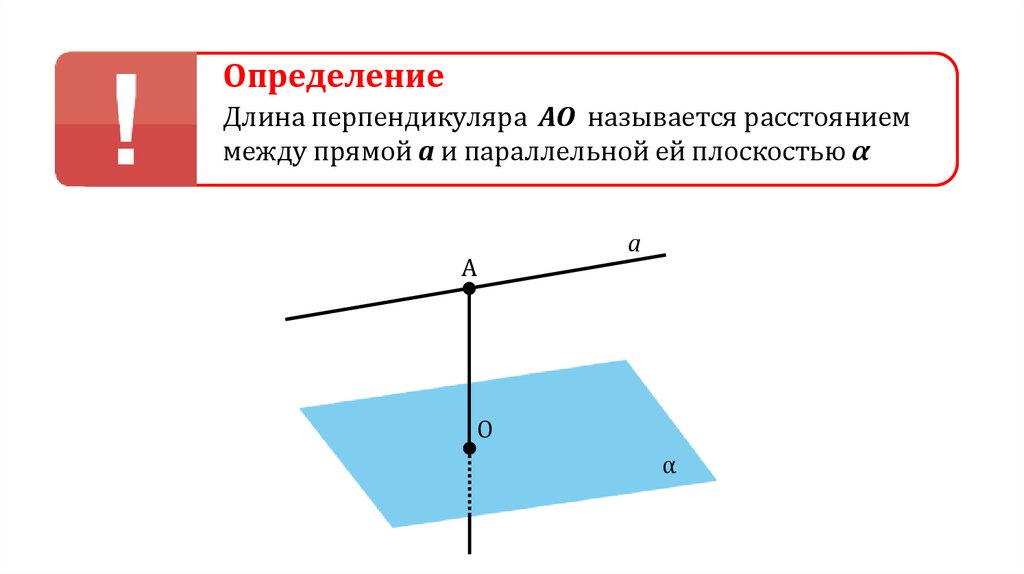
ОпределениеДлина перпендикуляра АО называется расстоянием
между прямой а и параллельной ей плоскостью α
a
A
O
α
37.
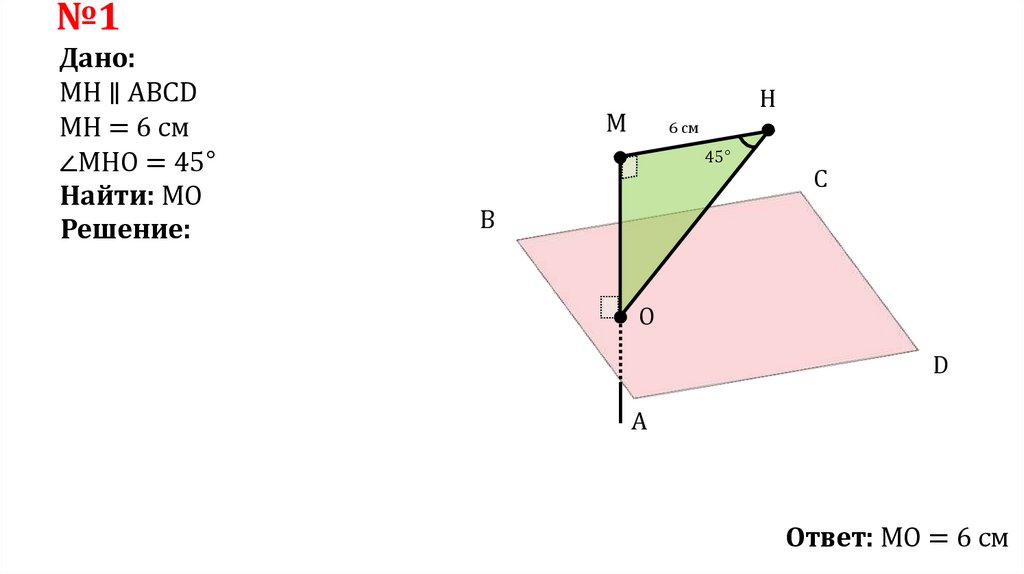
№1Дано:
МН ∥ ABCD
МН = 6 см
∠МНО = 45°
Найти: MO
Решение:
H
M
6 см
45°
C
B
O
D
A
Ответ: МО = 6 см
38.
Замечание 3Пусть прямые а и b скрещивающиеся. Тогда плоскость α,
проходящая через прямую а, параллельна прямой b
b
a
α
39.
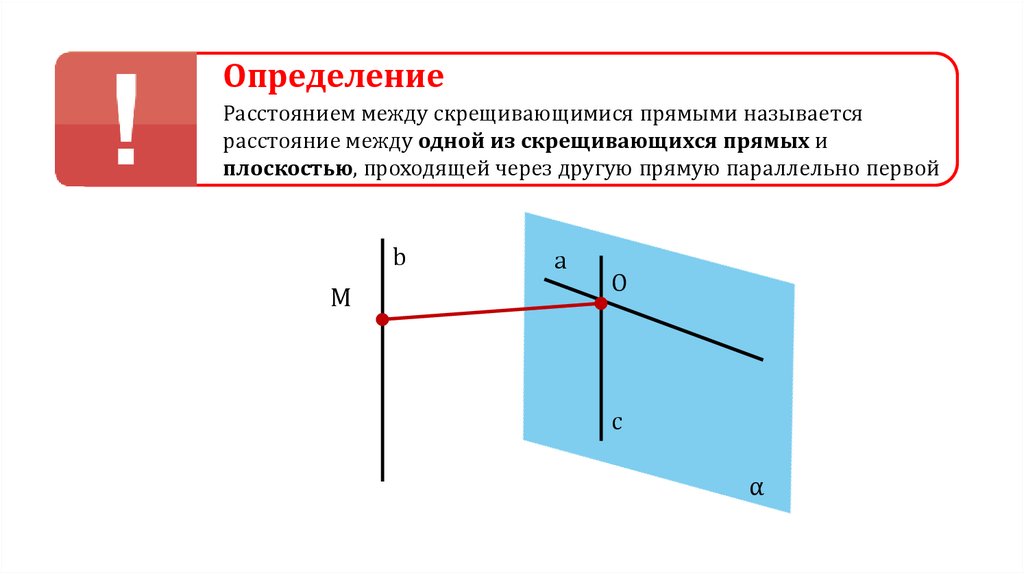
ОпределениеРасстоянием между скрещивающимися прямыми называется
расстояние между одной из скрещивающихся прямых и
плоскостью, проходящей через другую прямую параллельно первой
b
M
a
O
c
α
40.
13. Точка S лежит вне плоскости прямоугольникачто АВ = 8, ВС = 12, SA = 6, SB = 10, SD =
а) Докажите, что прямая SA перпендикулярна плоскости АВС.
б) Найдите расстояние от точки А до плоскости SCB.
АВСD.
Известно,
41.
42.
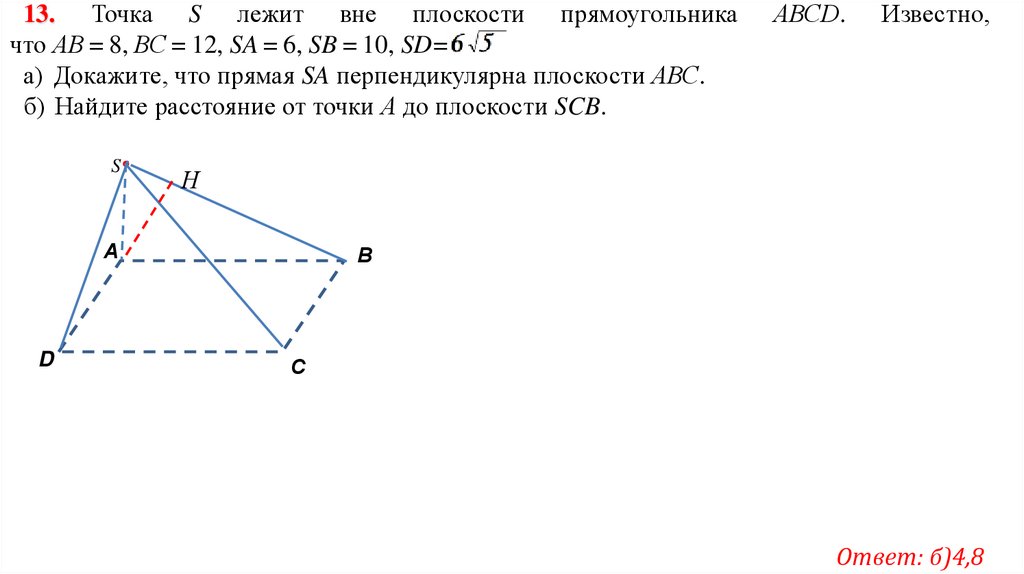
13. Точка S лежит вне плоскости прямоугольникачто АВ = 8, ВС = 12, SA = 6, SB = 10, SD=6
а) Докажите, что прямая SA перпендикулярна плоскости АВС.
б) Найдите расстояние от точки А до плоскости SCB.
S
Известно,
Н
А
D
АВСD.
В
С
Ответ: б)4,8








 mathematics
mathematics








