Обучение старшеклассников решению логарифмических неравенств

1.

Обучение старшеклассников решению
логарифмических неравенств

2.

Простейшие логарифмические неравенства
log5 f x 2 f x 25
f x 25,
log 1 f x 2
f x 0
5
f x 25,
log5 f x 2
f x 0
log 1 f x 2 f x 25
5

3.

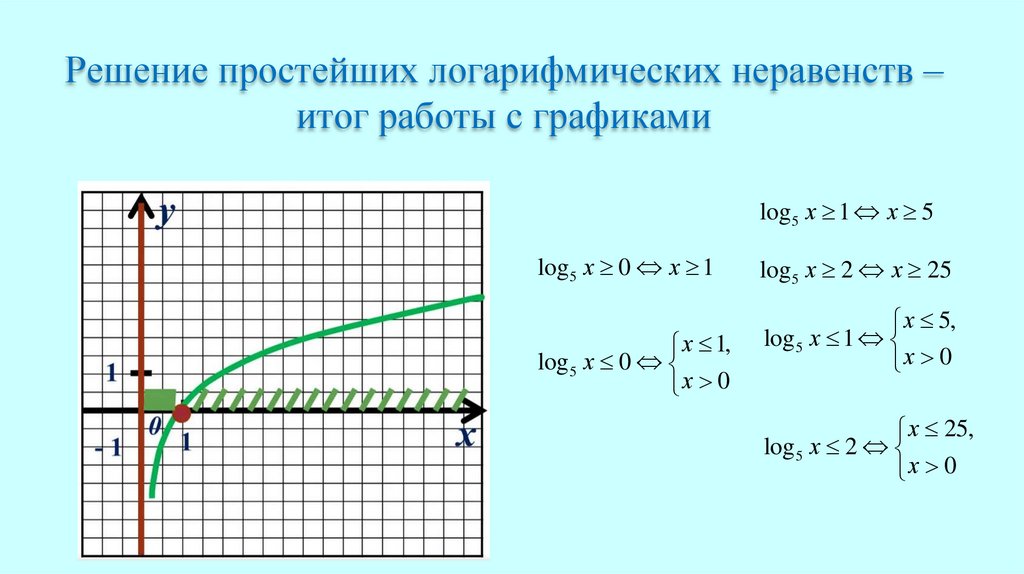
Решение простейших логарифмических неравенств –
итог работы с графиками
log 5 х 1 х 5
log 5 х 0 х 1
х 1,
log 5 х 0
х 0
log 5 х 2 х 25
х 5,
log 5 х 1
х 0
х 25,
log 5 х 2
х 0

4.

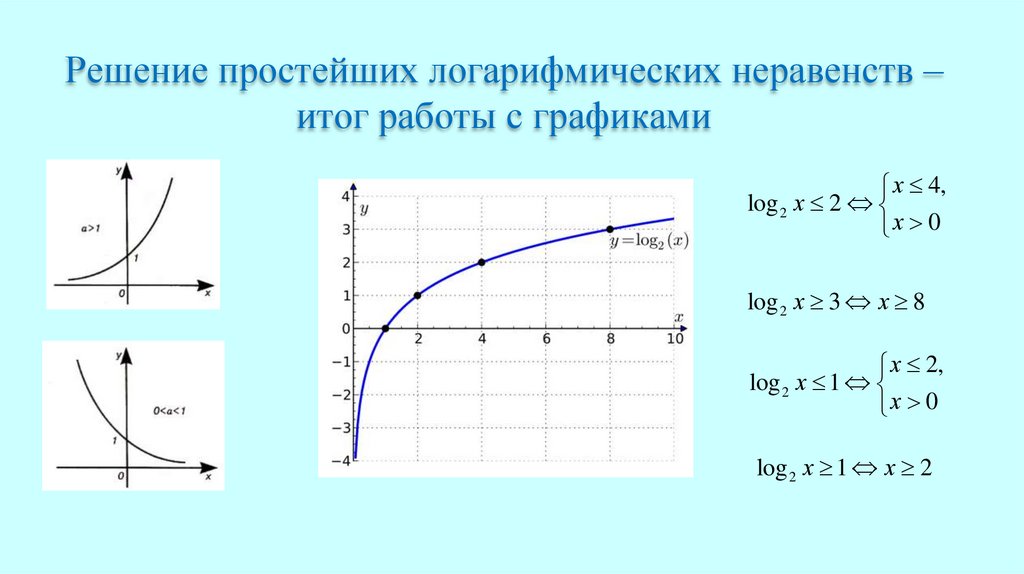
Решение простейших логарифмических неравенств –
итог работы с графиками
х 4,
log 2 х 2
х 0
log 2 х 3 х 8
х 2,
log 2 х 1
х 0
log 2 х 1 х 2

5.

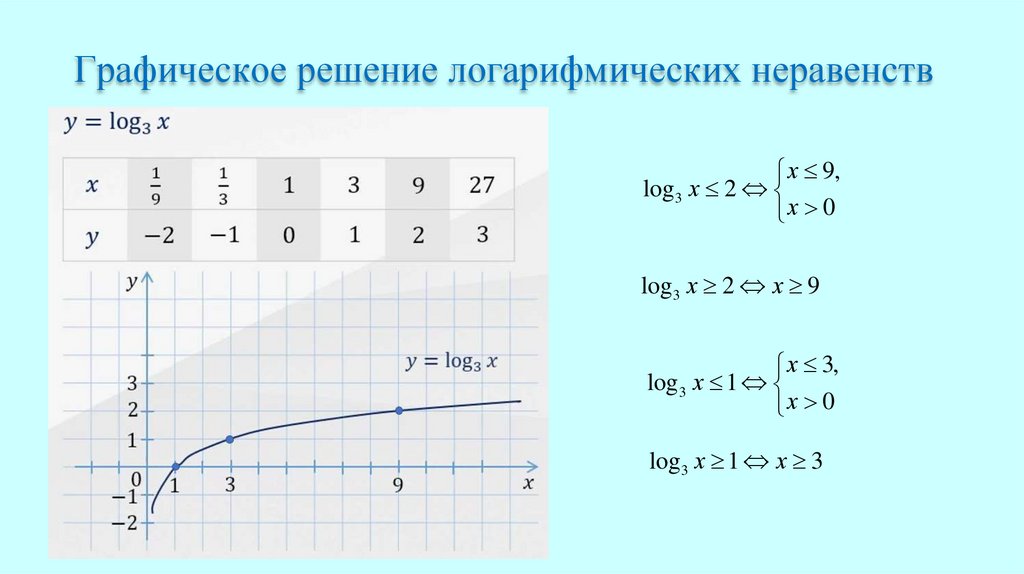
Графическое решение логарифмических неравенств
х 9,
log 3 х 2
х 0
log 3 х 2 х 9
х 3,
log 3 х 1
х 0
log 3 х 1 х 3

6.

Графическое решение логарифмических неравенств
х 9,
log 1 х 2
х 0
3
log 1 х 2 х 9
3
х 3,
log 1 х 1
х 0
3
log 1 х 1 х 3
3

7.

Простейшие логарифмические неравенства
f x x ,
log 5 f x log 5 x
x 0
f x x ,
log 0,5 f x log 0,5 x
f x 0
2
x
2 х 4 x 7,
2
log 1 x 2 х log 1 4 x 7
4 x 7 0;
4
4
х 1,
7
x 2 6 х 7 0,
х 1,
х 7,
4
7
4 x 7 0;
х 7.
х
;
4

8.

Опасно – интернет!

9.

Опасно – интернет!

10.

Основной метод – сведение к простейшим
свойства логарифмов
расширение
ОДЗ
посторонние
корни
log а xy log a x log a y
xy 0
x 0,
сужение ОДЗ y 0
потеря корни

11.

Основной вопрос
Можно ли выполнить данное
преобразование?
преобразование не
меняет ОДЗ
преобразование
расширяет ОДЗ
преобразования сужающие ОДЗ выполнять нельзя
Условия, чтобы отсеять
посторонние корни

12.

Заставляем думать:
достигаем метапредметные результаты обучения, формируя логические умения
1 log 6 4 х log 6 16 х 2
log 6 6 log 6 4 х log 6 16 х 2
log 6 (6 4 х ) log 6 16 х 2
Не кидаемся записывать ОДЗ!
Можно ли выполнить данное
преобразование?
При каких условиях?
2
6 4 х 16 х ,
4 х 6 4 х 0,
Подлагорифмические
4 х 0
4 х 0
выражения связаны точно
таким же знаком и меньшее
2 х 0,
х 2,
2 x 4.
из них больше нуля.
4 х 0
х 4
Ответ : 2;4 .
(Проговариваем!)
Используем, что 4–х > 0!

13.

Приучаем к красоте:
система задач
Не кидаемся записывать ОДЗ!
x 2 0,
2 log 1 x 2 log 1 x 2 x 2 1 log x 2 2 1 log x 2 x 2
1
2
2
12
2
Можно ли выполнить данное
x 2 0,
преобразование?
1
2
2
log 1 x 2 log 1 2 log 1 x x 2
2
2
2
x 2 0,
2
1
log 1 x 2 log 1 2 x 2 x 1
2
2
x 2 0,
x 2 0,
1
1
2
x 2 2 x 2 x 1 x 2 2 x 1
x 2,
Ответ : 2;5 .
2 x 5.
x 5
При каких условиях?
Подлагорифмические
выражения связаны
противоположным знаком и
меньшее из них больше
нуля. (Проговариваем!)
Используем, что x–2> 0!

14.

Приучаем к красоте:
log 4
3 x
2
log 0,25 х 3 log 1 х 7
x 7
4
система задач
Не кидаемся записывать ОДЗ!
Можно ли выполнить данное
преобразование?
При каких условиях?
x 7
2
log 1 х 3 log 1 х 7
4 3 x
4
4
Используем, что х–3> 0!
x 7
Подлагорифмические
0,
x 7 0,
3
x
выражения связаны
х 3 0,
противоположным знаком и
х 3 0,
2
( x 7) ( х 3)
2
log
(7
x
)
log
х
7
меньшее из них больше
1
log 1
1
log 1 х 7
4
4
3 x
нуля. (Проговариваем!)
4
4
log 1
x 7 0,
x 7 0,
3 х 7,
3 х 7,
х
3
0,
х
3
0,
x 3; 6 .
1 x 7
x 6
2
2
7 x х 7
x 7 х 7
Ответ : 3; 6 .
Используем, что х–7< 0!

15.

Система задач
Не кидаемся записывать ОДЗ!
x
2 1
Можно ли выполнить данное
2 log 5 x 2 log 5
log
8
x
5
5
x
1 x
преобразование?
При каких условиях?
Используем, что х > 0! х 0,
Проговариваем как связаны
х 0,
x
подлагорифмические
2
0,
x
2 1
выражения.
log 7 x 2 log 7 1 x log 7 8 x x 5
1 x
2 1
log
2
x
1
x
log
8
x
5
7
7
x
1
х 0,
0
x
,
0
x
1,
0
x
1,
5
1
x
0,
2
3
2
5
x
1
2
x
1 0
10
x
2
x
5
x
1
0
2
1
2 x 1.
2 x 1 x 8 x 2 5
x
1 2
Ответ : 0;
;1 .
5 2

16.

Система задач
1
2 log 2 1 2 x log 2 2 log 2 4 x 2 6 x 1
x
1 2 x 0,
2
1
2
log 2 1 2 x log 2 x 2 log 2 4 x 6 x 1
1 2 x 0,
Используем, что 1–2x > 0!
1 2 x
0,
x
2 1 2x
2
log 2 1 2 x :
log 2 4 x 6 x 1
x
1 2 x 0,
x 0,
2
log 2 1 2 x x log 2 4 x 6 x 1
1
x
,
1 2 x 0,
2
1
1
x 0,
x 0,
x .
6
2
1 2 x x 4 x 2 6 x 1 6 x 2 5 x 1 0
Не кидаемся записывать ОДЗ!
Можно ли выполнить данное
преобразование?
При каких условиях?
Подлагорифмические
выражения связаны точно
таким же знаком и меньшее
из них больше нуля.
(Проговариваем!)
1 1
Ответ : ; .
6 2

17.

Система задач
9 log12
x 1
x 2 3 x 4 10 log
log12 x 2 3 x 4
12
9
x 4
Не кидаемся записывать ОДЗ!
x 1 10
log
9
9
12
x 4
x 1 x 4 0,
9
10
x 1 x 4
10
log12
9
x 1
x 1 x 4 0,
10
log12 x 4 10
x 1 x 4 0,
x 1 x 4 0,
10
log
x
4
10
log
x
4
1
12
12
x 1 x 4 0,
x 1 x 4 0,
x 4 12,
4 x 4 12,
x 4 0.
x
4
0;
Ответ : 8; 1 4;16 .
Можно ли выполнить данное
преобразование?
При каких условиях?
Подлагорифмические
выражения связаны точно
таким же знаком и меньшее
из них больше нуля.
(Проговариваем!)

18.

log 4 6 6 х log 4 x 2 5 х 4 log 4 х 3 log 4 6 x 1 log 4 x 1 x 4 log 4 х 3
x 1 x 4 0,
х 3 0,
log 4 6 x 1 log 4 x 1 x 4 х 3
x 1 x 4 0,
х 3 0,
6 x 1 x 1 x 4 х 3 ,
6 x 1 0
x 4 0,
x 4,
х 3 0,
х 3,
2
6 x 4 х 3 , x х 6 0,
x 1 0
x 1
3 x 1,
2 x 1.
х 2 х 3 0
Не кидаемся записывать ОДЗ!
Можно ли выполнить данное
преобразование?
При каких условиях?
Подлагорифмические
выражения связаны точно
таким же знаком и меньшее
из них больше нуля.
(Проговариваем!)
Используем, что х–1< 0!

19.

Поменяем знак неравенства
log 4 6 6 х log 4 x 2 5 х 4 log 4 х 3 log 4 6 x 1 log 4 x 1 x 4 log 4 х 3
x 1 x 4 0,
х 3 0,
log 4 6 x 1 log 4 x 1 x 4 х 3
Не кидаемся записывать ОДЗ!
Можно ли выполнить данное
преобразование?
x 1 x 4 0,
При каких условиях?
x 1 x 4 0,
х 3 0,
х 3 0,
Подлагорифмические
6
x
1
x
1
x
4
х
3
,
6 x 1 x 1 x 4 х 3 ,
выражения связаны точно
6 x 1 0
таким же знаком и меньшее
x 4 0,
x 4,
из них больше нуля.
х 3 0,
х 3,
(Проговариваем!)
2
Добавляем условие!
6 x 4 х 3 , x х 6 0,
x 1 0
x 1
Используем, что х–1< 0!
3 x 1,
3 x 2.
х 2 х 3 0

20.

Не всегда бывает красиво!
log 1 18 9 x log 1 x 2 6 x 5 log 1 x 2
3
3
3
log 1 9 x 2 log 1 x 1 x 5 log 1 х 2
3
3
3
x 1 x 5 0,
х 2 0,
log 1 9 x 2 log 1 x 1 x 5 х 2
3
3
x 1 x 5 0,
x 1 x 5 0,
х 2 0,
х 2 0,
9 x 2 x 1 x 5 х 2 , х3 4 х 2 2 х 8 0
Не кидаемся записывать ОДЗ!
Можно ли выполнить данное
преобразование?
При каких условиях?
Подлагорифмические
выражения связаны
противоположным знаком и
меньшее из них больше
нуля. (Проговариваем!)
x 1 x 5 0,
x 1 x 5 0,
х 2 0,
х 2 0,
x 4 0
2
x
4
x
2
0
x 1 x 5 0,
Никакой красоты! Даже если добавить условие х – 2 < 0!
2 x 1.
2 x 4
Ищем красоту!

21.

Чтобы получить сертификат
фото решения 2-х неравенств прикрепить в
качестве квитанции за оплату мероприятия
log 1 5 x 1 log 1 25 х 2
3
3
log 6 21 7 х log 6 x 8 х 15 log 6 х 3
2
Спасибо за внимание!