Сложное движение точки

1.

СЛОЖНОЕ ДВИЖЕНИЕ
ТОЧКИ

2.

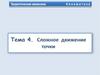
- такое движение, при котором тело участвует одновременно в двух
или нескольких движениях

3.

4.

5.

6.

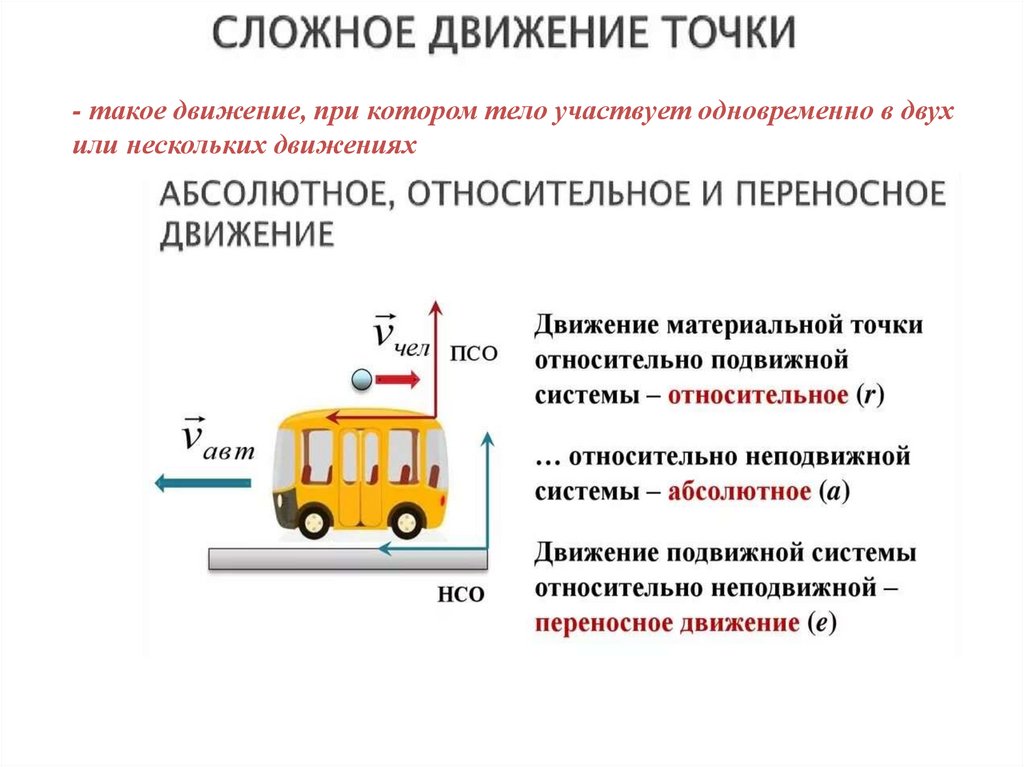
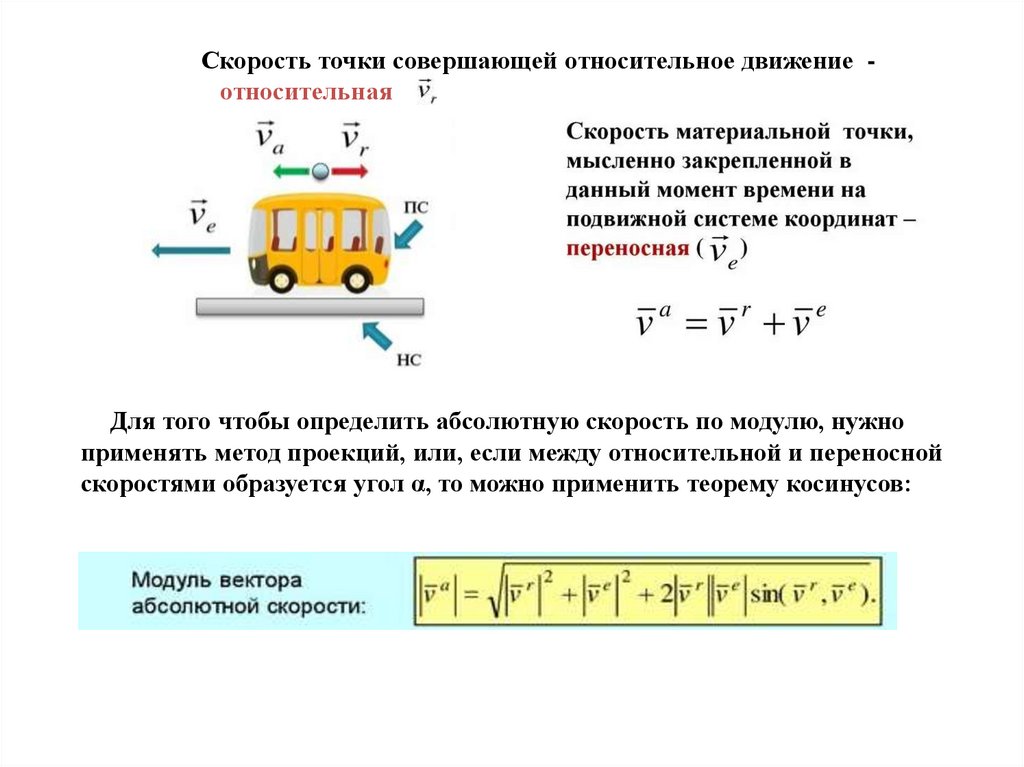
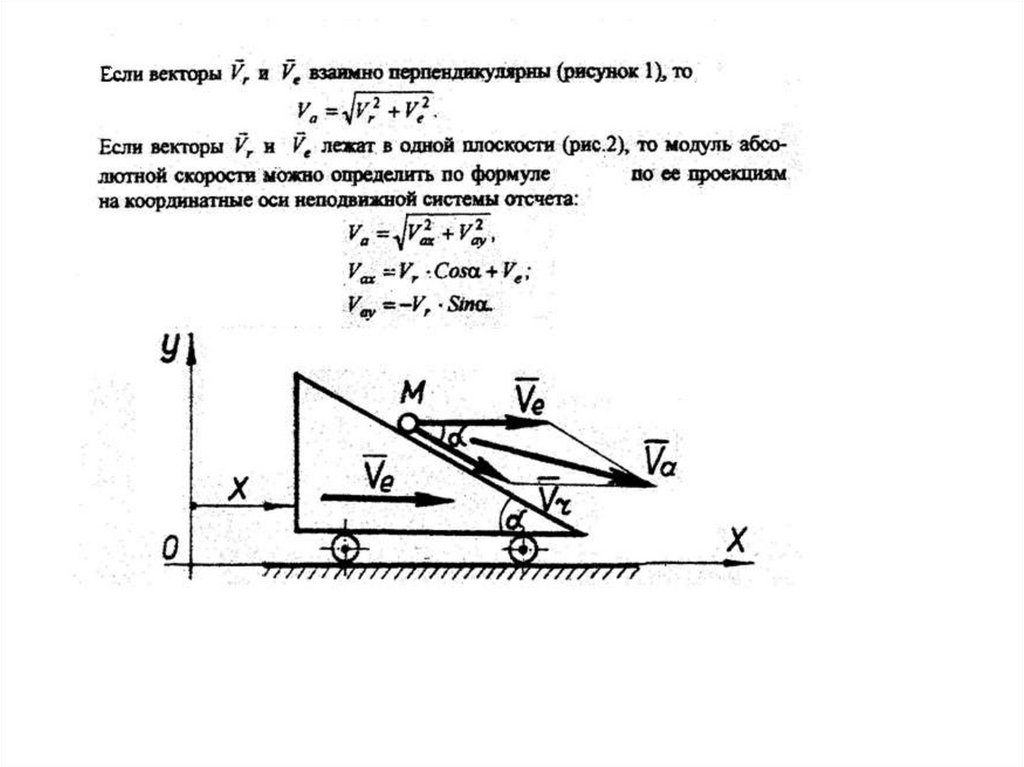
Скорость точки совершающей относительное движение относительная
Для того чтобы определить абсолютную скорость по модулю, нужно
применять метод проекций, или, если между относительной и переносной
скоростями образуется угол α, то можно применить теорему косинусов:

7.

8.

На рисунке (а) показан квадрат, вращающийся в плоскости чертежа вокруг
неподвижной точки. По стороне квадрата движется точка M. Она участвует в
двух движениях, поэтому можно ввести две системы отсчета: неподвижную,
например, O1x1y1z1 — по отношению к которой вращается квадрат и
подвижную Oxyz, скрепленную с квадратом, по оси Oy которой движется
точка M рисунок (б).
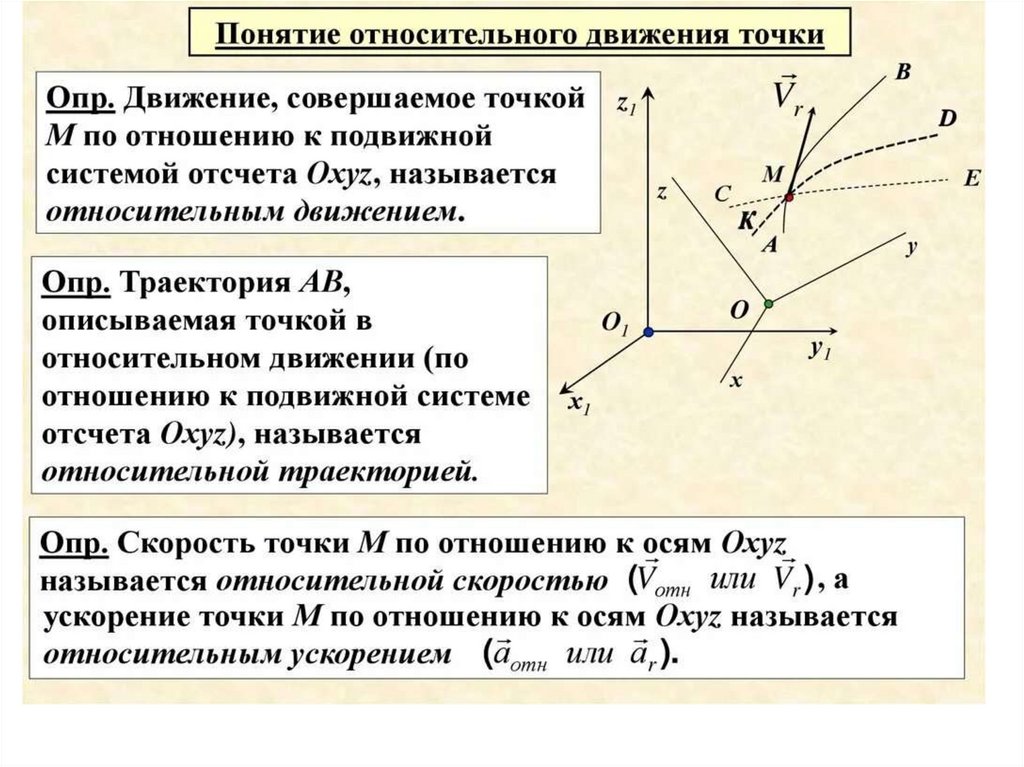
Движение точки M по стороне квадрата (по оси Oy скрепленной с квадратом
подвижной системы) является относительным — скорость в этом движении Vr.
Вращение точки M вместе с квадратом — переносное движение, скорость в
этом движении — Ve. Абсолютное движение является результатом сложения
переносного и относительного движений.

9.

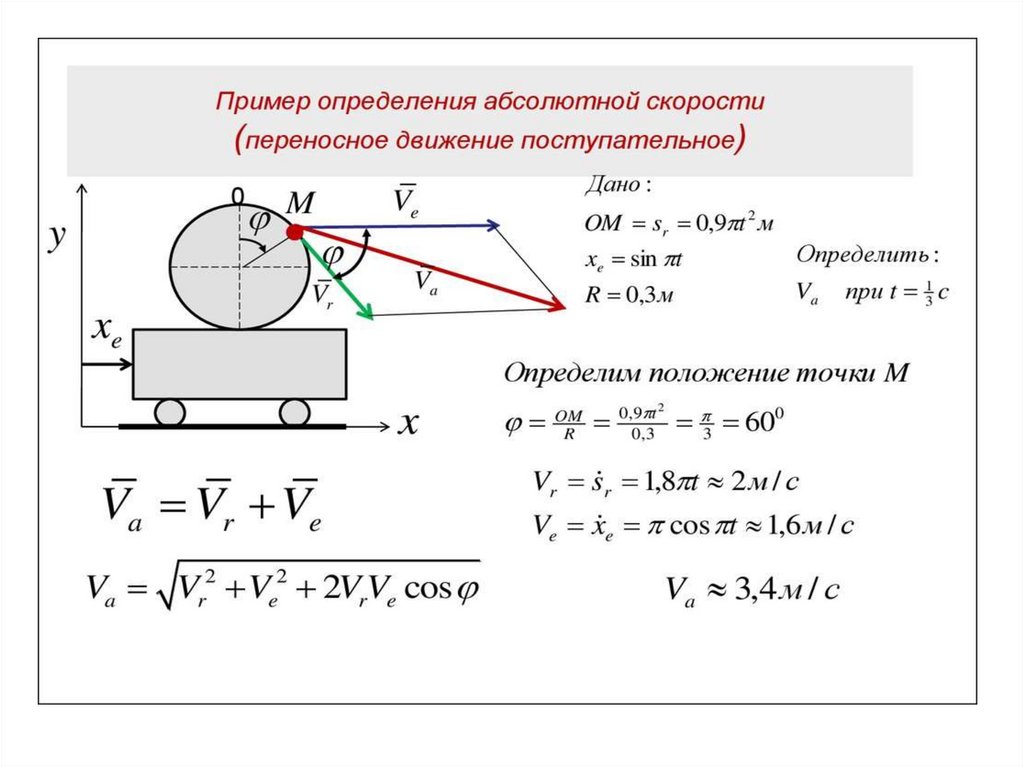
Теорема о сложении скоростей:
Вектор абсолютной скорости, Va , представляет собой
геометрическую сумму векторов скоростей точки при относительном,
Vr , и переносном, Ve , движениях:
Эти векторы направлены по касательным к соответствующим траекториям.
Например, если переносным является вращательное движение, то
переносной скоростью Ve для точки М будет скорость той точки вращающегося
тела( подвижной системы отсчета), с которой в данный момент совпадает
точка М, движущаяся относительно вращающегося тела.
Численное значение скорости Ve зависит от
угловой скорости вращающегося тела и
расстояния h от точки до оси вращения. Вектор
относительной скорости Vr направлен вдоль
прорези вращающего тела.
Модуль абсолютной скорости определяется по
формуле
где α -угол между векторами Vr и Ve .

10.

11.

12.

Абсолютное ускорение точки
Абсолютное ускорение точки, при ее сложном движении, будет
складываться из трех составляющих:

13.

14.

15.

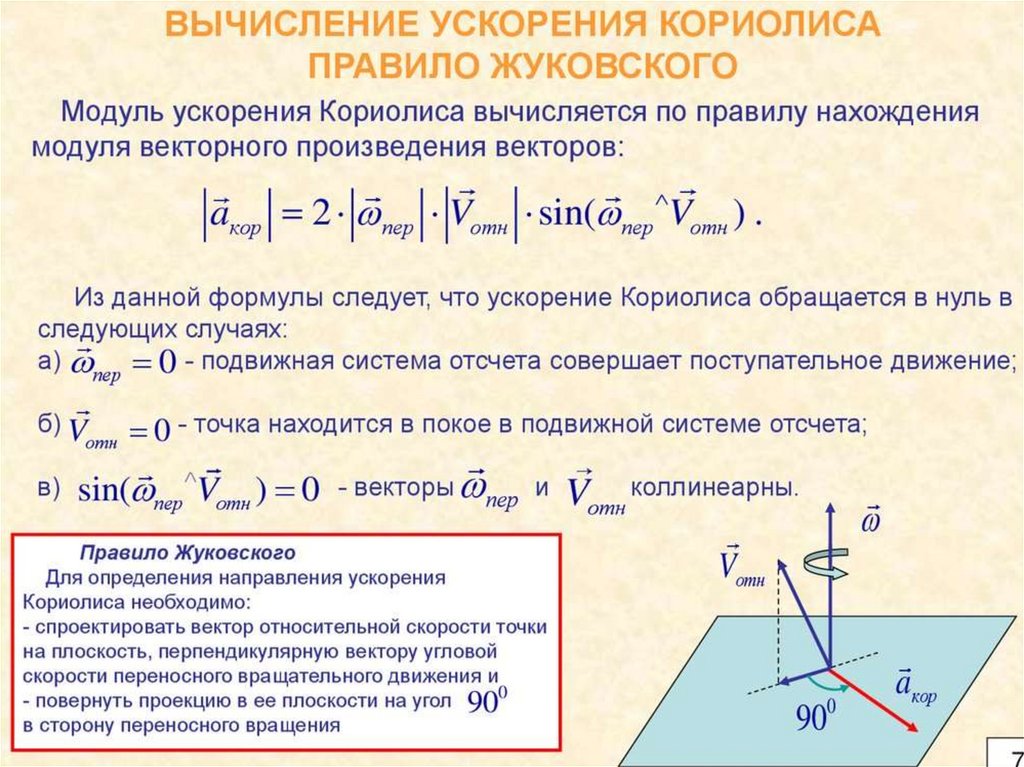
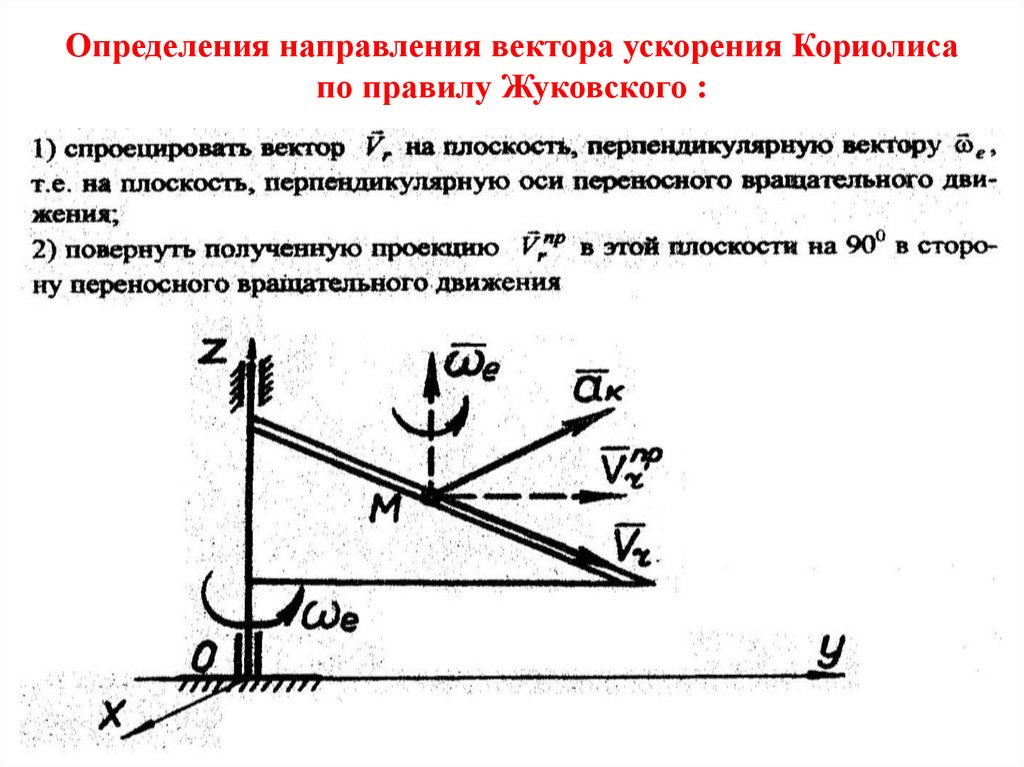
Определения направления вектора ускорения Кориолиса
по правилу Жуковского :