Лекция_2

1.

“Исследовательский Центр
имени М.В. Келдыша”
Теория теплообмена
Курс лекций В. Я. Лихушина
Лекция №1
Москва - 2007
1

2.

Основы молекулярно-кинетической теории
Движение молекул в потоке газа
n – число частиц в единице объема – велико.
Физически малый элемент объема: V L L
n V – велико.
молекул
Например: H 100 км; P 4 10 7 кг / см 2 ; n 3,5 1010
3
мм
3
среднее расстояние между молекулами: l м 3 10 мм
Обычно - l м L
Время изменения нестационарного состояния: L U
Физически малые промежутки времени: - число частиц в объеме не меняется.
1). Описание дискретной совокупности молекул –
непрерывными, дифференцируемыми функциями .
2). Из-за n-велико → использование статистических методов.
За N в V
не меняется
Осредненное и хаотическое движение, модель упругих шариков ( i , mi ) , в более
строгой теории молекулы – центры точечных сил.
ij rij - потенциал взаимодействия i и j молекул, от расстояния между ними
Учитываем
только парный характер взаимодействия.
r r
rij rj ri
X ij rij j i - сила, с которой j молекула действует на i
rij
ri rj
X ji rij
X ij - По третьему закону Ньютона
rij
2

3.

Основы молекулярно-кинетической теории
Типичный потенциал
взаимодействия двух молекул.
Модель точечных центров и
упругих твердых шариков
ij
y
x
z
ij
i j
2
ij
vy
rij
Рис. 3
dvy
v dv dvz
y
vy
vx
vz
z
py
x
px
zpz
Для описания движения молекул: Пространство
координат. Пространство скоростей или пространство
импульсов. Совокупность n молекул в данный момент
– n точек в x , v .
Функция распределения: f x, y , z, v x , v y , v z , или
f 1 x, y, z, px , p y , pz , определяет число молекул dn
из общего числа n в единице объема, которые в данный
момент имеют скорости в диапазоне: v , v dv
dn f x, y , z, v x , v y , vz , dv x dv y dvz
Из условия
нормировки:
x
x
x
v y , v y dv y
v z , v z dv z
n f x, y, z , v x , v y , v z , dv x dv y dv z или сокращенно:
n
f
v
,
r
,
d
v
Рис.
4
vz
Для многокомпонентного газа: dni fi vi , ri , dvi
d
v
3
i dvix dviy dviz
1
dni f i pi , ri , dpi
x
vx

4.

Основы молекулярно-кинетической теории
Зная функцию распределения легко определить осредненное значение любых функций
скоростей и импульсов частиц. Найдем среднюю скорость:
Однокомпонентный газ
1
vср v f v , r , dv v0 x, y, z , - это также среднемассовая скорость, так как
массы всех частиц одинаковы
n
Скорость с x, y, z, v v0 x, y, z, называется скоростью теплового движения
молекул.
Тогда средняя скорость теплового
движения газа:
1
v
1
cср c f v , r , dv v f v , r , dv 0 f v , r , dv v0 v0 0
n
n
n
Многокомпонентный газ
m
v
f
v
,
r
,
d
v
i i i
i
Средне массовое значение скорость :
vср i 1
v0 x, y , z,
ni mi
- где ni mi i - плотность i-ого компонента
i 1
n
m
плотность
газа
в
целом
i i
v0 mi vi fi v , r , dvi i vi ср
i 1
Скорость теплового движения i-ого
компонента: сi x, y, z, vi v0 x, y, z,
1
ci ср vi ср v0 ci fi v , r , dvi Vi
ni
i 1
- скорость диффузии
i 1
4

5.

Основы молекулярно-кинетической теории
Произведение скорости диффузии i-ого компонента Vi на его
i ni mi
плотность
называется диффузионным потоком i-ого компонента:
ji iVi
1
Зная, что
v0 i vi ср
Vi ci fi v , r , dvi vi ср v0 ci ср и
n
i 1
легко найти :
j
V
v
v
v
v
i i i i i ср i 0 0 0 0
i 1
i 1
i 1
i 1
Итак, в любой многокомпонентной смеси сумма диффузионных потоков всех
компонентов всегда тождественно равна нулю:
ji 0
i 1
Это тождество отражает тот факт, что среднемассовая скорость
теплового движения всех компонентов всегда равна нулю:
mi niVi
c ср i 1
n m
i 1
i
0
i
5

6.

Основы молекулярно-кинетической теории
Процессы трения
и теплообмена
Площадка dS движется со скоростью v0 через нее идет поток со скоростью c
за счет теплового движения
потоку количества движения
Поверхностная сила, действующая на единицу площади, равна количеству
движения, переносимому через dS в единицу времени через единицу площади за
счет теплового движения.
n
c
Π n m cn c f dv
x,y,z
m i cn cx f dv j cn c y f dv k cn cz f dv
dS
единичные
вектора;
Рис. 5
i , j,k
Полную характеристику действующих сил дают три вектора: Π x , Π у , Π z
2
Π xx Π xy Π xz
Π x mn cx ср i mn cx c y ср j mn cx cz ср k
2
Π Π уx Π уy Π уz
Π y mn c y cx ср i mn c y ср j mn c y cz ср k
Π zx Π zy Π zz
2
Π z mn cz cx ср i mn cz c y j mn cz ср k
ср
- тензор поверхностных сил;
Компоненты
тензора могут быть определены, если известна функция распределения:
Π m c c f dv ,
x, y , z x, y , z
6

7.

Основы молекулярно-кинетической теории
Процессы трения и теплообмена
Обычно тензор поверхностных сил разделяют на тензор давления и тензор
вязких напряжений. По определению давлением называют:
p
Π xx Π уy Π zz
3
Тензор вязких сил :
n
x,y,z
dS
Рис. 6
c
p 0 0
1 0 0
, тензор давления : Ρ 0 p 0 p 0 1 0 p
0 0 1
0 0 p
p 0 0 Π xx Π xy Π xz
Τ Ρ Π 0 p 0 Π уx Π уy Π уz
0 0 p Π zx Π zy Π zz
Для теплового потока, аналогично, рассматривается площадка
dS, движущуюся со скоростью v0 , через нее движутся
молекулы за счет теплового движения .
Поток тепла, переносимый через единицу площади в единицу
времени, равен потоку кинетической энергии молекул,
переносимому через единицу площади dS в единицу времени
за счет теплового движения.
mn
mn
2
2
mn
c2
q
c
c
q
c
c
2
z
z
ср
x
ср
qn m cn
f dv
cn c ср x
2
mn
2
2
2
2
7
qy
c y c ср
2

8.

Основы молекулярно-кинетической теории
Процессы трения и теплообмена
mn 2
q
c c ср
2
c2 сx2 с2y сz2
Для многокомпонентного газа:
Π m c c f dv
Тензор поверхностных сил, трения, давления и тепловой поток определяются
аналогично
Π mi ci ci fi dvi mi ni ci ci ср
i 1
x, y , z x, y , z
i 1
Π
p 0 0 Π
p
Τ
Ρ
Π
0 p 0 Π
mi ni ci ci ср p
0 0 p Π
3
i 1
ci2
mn
q mi ci
fi dvi i i c i ci2 ср
ci2 cix2 ciy2 ciz2
2
2
i 1
i 1
xx
уx
zx
Π xy
Π уy
Π zy
Π xz
Π уz
Π zz
Для многокомпонентных смесей в отличие от однородного газа тепловое движение
молекул обуславливает не только перенос количества движения и энергии, но и
перенос массы отдельных компонентов, т. е. процесс диффузии:
1
Vi ci fi dvi
ni
Все величины,
характеризующие перенос количества движения, энергии, массы8–
Π , q, Vi можно определить, если известна f – функция распределения.

9.

Основы молекулярно-кинетической теории
Эта функция неприменима
для строгого определения
Для термодинамического
Π , q, Vi
равновесия – функция
1) Вязкость, диффузия, теплопроводность необратимые
распределения Максвелла:
процессы;
2) Функция Максвелла четная относительно скорости ci ,
32
mi ci2
mi 2 kT
интегралы в выражениях Π , q ,V берутся в
0
f i ni
e
симметричных пределах от нечетных функций, то
2 kT
интегралы тождественно равны нулю (кроме ).
Однако на ее основе можно вычислить:
p nkT RT
p
Π xx Π уy Π zz
- уравнение
состояния газа;
3
Π m c c f dv
R k m
- газовая
постоянная;
Рассмотрим основные положения элементарной молекулярно-кинетической теории,
основанные на понятии длины свободного пробега.
Нулевое приближение fi0 используем для определения осредненных функций от
скорости теплового движения:
Наряду с функцией распределения, определяемой:
32
m c x2 c 2y cz2
m
2 kT
dn n
dcx dc y dcz удобно ввести f для абсолютных скоростей
e
2 kT
32
mс 2
m
2
dn 4 n
e 2 kT с dc число молекул в шаровом слое с+dс 9
2 kT

10.

Основы молекулярно-кинетической теории
В молекулярно-кинетической теории обычно рассматривают следующие
характеристики теплового движения молекул:
32
1). c 4
0
m
e
2 kT
2).
mс 2
2 kT
с 3dc
32
m
c 4
e
2 kT
0
2
2 mс
d
с e 2 kT 0
3).
dc
mс 2
2 kT
8kT
m
- среднеарифметическая скорость
теплового движения молекул;
3kT
с dc
m
4
- среднеквадратичная скорость
теплового движения молекул;
2
cв
2kT
m
- наиболее вероятная скорость
теплового движения молекул;
4). Абсолютное значение
теплового движения молекул
средней относительной скорости
первого сорта (c1), относительно второго сорта ( c2 ).
21
2
2
2
c1 c2 ср c1x c2 x c1 y c2 y c1z c2 z
cp
ср
Для молекул первого
сорта (c1), вероятность иметь скорость в пределах объема
dc1x dc1 y dc1z dc1 будет
32
m c12x c12y c12z
m
0
2 kT
dp1 n
e
dc
dc
dc
f
c
d
c
1x
1y
1z
1
1
1 10
2 kT

11.

Основы молекулярно-кинетической теории
Для молекул второго
сорта (c2 ), вероятность иметь скорость в пределах объема
dc2 x dc2 y dc2 z dc2 будет
32
m c22 x c22 y c22 z
m
0
2 kT
dp2 n
e
dc
dc
dc
f
c
d
c
2x
2y
2z
2
2
2
2
kT
Вероятность нахождения относительной скорость 21 в пределах объема
21... d 21 21 будет d dp1dp2 следовательно
c c c c c c c c
32
3 2
21 ср m1 m2 c1x c2 x 2 c1 y c2 y 2 c1 y c2 y 2
2 kT 2 kT
2
mc1 mc22
8kT m1 m2
2 kT
e
dc1dc2
m1m2
2
21
ср
1
2 ср
1x
2x
2
1y
2y
2
1z
2z
8kT m1 m2
21 ср 12 ср
m1m2
m1m2
12 - приведенная масса
m1 m2
m
8kT
Для однородного газа m1 m2 m
2
2 с
12
ср
2
m
Относительная скорость частиц в однородном газе в 2 больше, чем средняя
абсолютная скорость каждой молекулы.
11
cp

12.

Основы молекулярно-кинетической теории
2
12
1
n2
S1
S3
S2
2
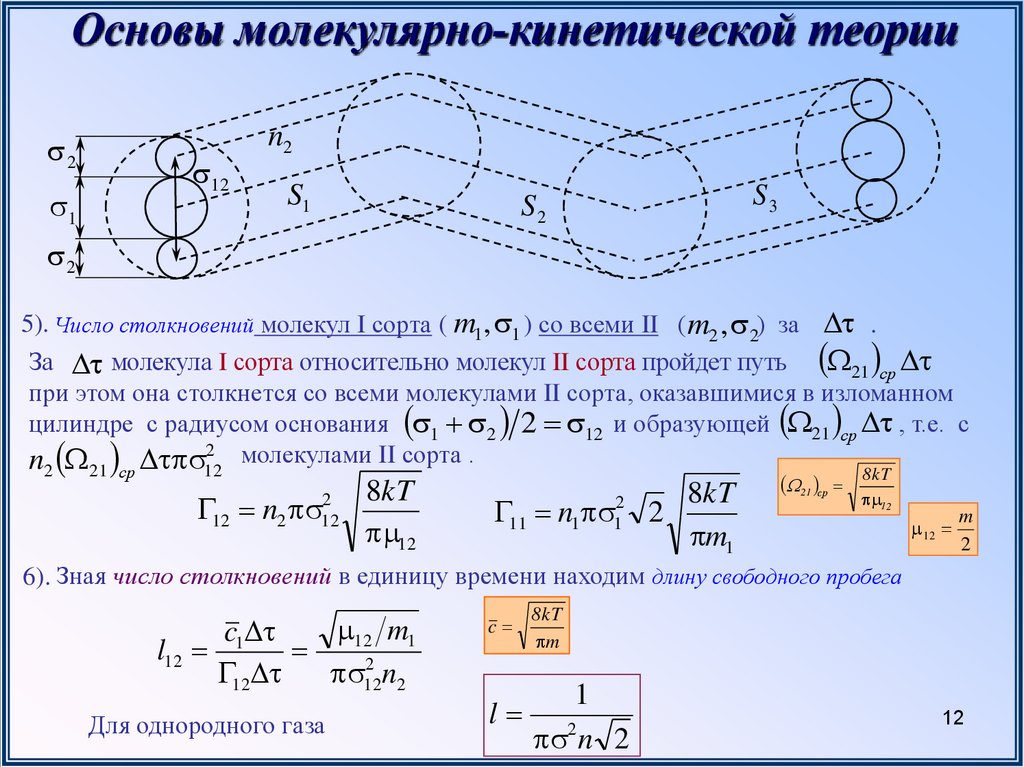
5). Число столкновений молекул I сорта ( m1, 1 ) со всеми II ( m2 , 2) за .
За молекула I сорта относительно молекул II сорта пройдет путь 21 ср
при этом она столкнется со всеми молекулами II сорта, оказавшимися в изломанном
цилиндре с радиусом основания 1 2 2 12 и образующей 21 ср , т.е. с
n 2 молекулами II сорта .
2
21 ср
12
2
12 n2 12
8kT
12
11 n1 12 2
8kT
m1
21 ср
8 kT
12
12
m
2
6). Зная число столкновений в единицу времени находим длину свободного пробега
12 m1
c
l12 1
2
12
12
n2
Для однородного газа
c
8 kT
m
l
1
2n 2
12

13.

Основы молекулярно-кинетической теории
После одного удара свойства молекул частично сохраняются
Рассмотрим для примера сохраняемость скорости, при упругом ударе в однородном газе.
v1 v2 v1 v2
m1 m2
Из законов
v1 v1 v2 v1
сохранения
вытекает, что v2 v2 v2 v1
12 v2 2 v12 v22
v
2
- единичный вектор, направленный в момент удара из центру «1» в центр«2».
При столкновении «1» со всеми остальными в пред. 4 - тел. угол.
1
Спроецируем скорость v1 «1» молекулы после удара на первоначаль
ное
направление
и
осредним
по
всем
возможным
и v1 , v2
v
v
Рис. 7
1
1
2 2
v1 v12 v2 v1 v1
v
v1
1 v2 cos 2 cos 1 v1 cos2 1
v1 v1
v1
v1
v1
1 - угол между v1 и 2 - угол между v2 и
2
2
1
1
v
v
v
Осредняя, получим: v1 1 1 1 cos2 1 1 где sin 2 1
ср
v
v
v 2
2
1 ср 1
ср 1 ср
Таким образом после одного столкновения в среднем сохраняется половина проекции
скорости на первоначальное направление.
Такие свойства молекул, как количество движения, энергия и концентрация
сохраняются на длине несколько большей длины свободного пробега:
l l
l l
lg i gi l
13