Лекция № 4

1.

Повторные испытания.
Формула Бернулли

2.

В научной и практической деятельности часто
приходится проводить многократн о повторяющиеся
испытания в сходных условиях. Как правило, при этом
результаты предшествующих испытаний никак не
сказываются на последующих. Очень важен простейший
тип таких испытаний, когда в каждом из опытов
некоторое событие появляется с одной и той же
вероятностью.
Последовательность n независимых испытаний, в
каждом из которых может некоторое событие A с
вероятностью p или противоположное ему событие A
с вероятностью q 1 p, называется схемой Бернулли.

3.

Рассмотрим задачу, относящуюся к схеме Бернулли ,
о вычислении вероятности того, что при n испытаниях
событие A произойдет ровно k раз, и, следовательно, не
произойдет n k раз. Искомая вероятность обозначается
Pn (k ) или P(n, k ).
Теорема. Если производится n независимых испытаний,
в каждом из которых вероятность появления события A
равна p, а вероятность его непоявления q 1 p, то
вероятность того, что событие A произойдет ровно k раз
определяется формулой Бернулли
n!
k k n k
Pn (k ) Cn p q
p k q n k .
(1)
k!(n k )!

4.

Докажем формулу Бернулли . Вероятност ь события,
состоящего в том, что в n испытаниях событие A наступит
k раз и не наступит n k раз, по теореме умножения
вероятностей независимы х событий равна p k q n k . Таких
событий может быть столько, сколько можно составить
сочетаний из n элементов по k элементов, то есть Cnk . Так
как эти события несовместны, то искомая вероятность
равна сумме вероятностей всех таких событий. Поскольку
их вероятности одинаковы и равны p k q n k , то вероятность
появления в n испытаниях события A k раз равна
произведению вероятности p k q n k на число Cnk таких
событий, то есть
Pn (k ) Cnk p k q n k .

5.

Легко заметить, что вероятности Pn (k ), k 0, n
являются коэффициен тами при x k в разложении бинома
(q px) n по степеням x (формула бинома Ньютона ) :
(q px) n Cn0 q n Cn1 q n 1 px Cn2 q n 2 p 2 x 2
Cnk q n k p k x k Cnn p n x n . (2)
Поэтому совокупность вероятностей Pn (k ) называют
биноминальным законом распределения вероятност ей,
а функцию ( x) (q px) n производящ ей функцией для
последовательности независимых опытов.

6.

В схеме Бернулли все возможные несовместные между
собой исходы испытаний ( группа событий) состоят в
появлении события A 0 раз, 1 раз, 2 раза , , n раз, для них
n
P (k ) 1.
k 0
n
Это соотношение можно получить и из формулы (2)
при x 1, то есть
n
n
k 0
k 0
k n k k
n
P
(
k
)
C
q
p
(
p
q
)
1.
n
n

7.

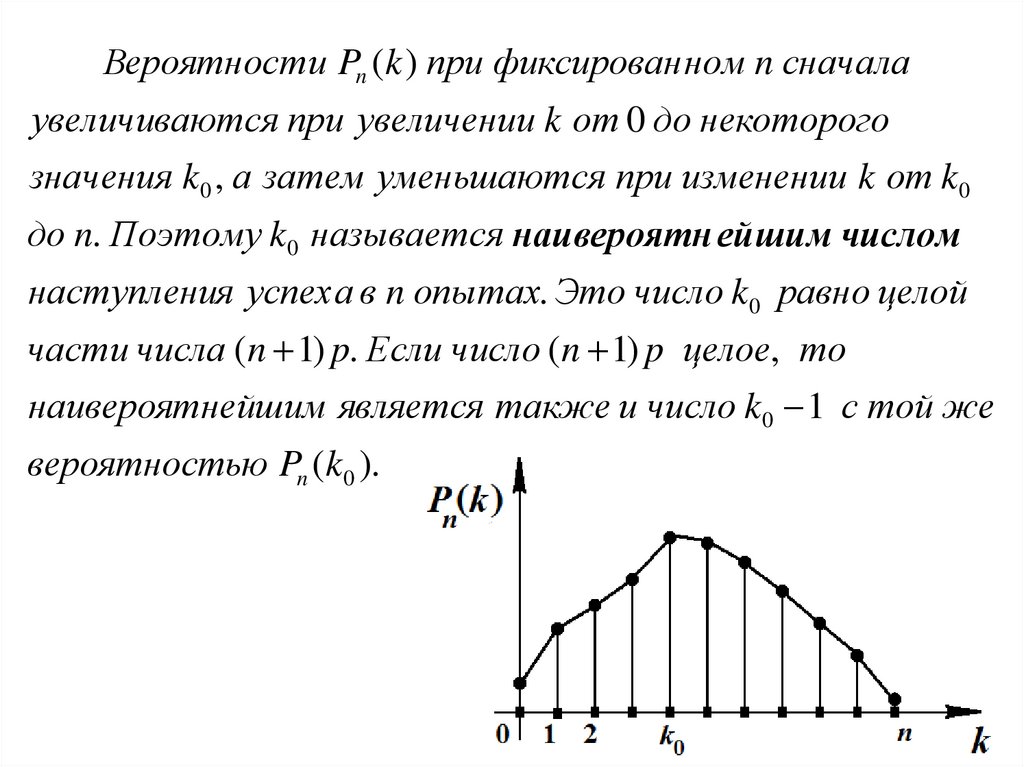
Вероятност и Pn (k ) при фиксирован ном n сначала
увеличиваются при увеличении k от 0 до некоторого
значения k0 , а затем уменьшаются при изменении k от k0
до n. Поэтому k0 называется наивероятн ейшим числом
наступления успеха в n опытах. Это число k0 равно целой
части числа (n 1) p. Если число (n 1) p целое, то
наивероятнейшим является также и число k0 1 с той же
вероятностью Pn (k0 ).

8.

Если в каждом из независимых испытаний вероятности
наступления события A разные, то вероятность того, что
событие A наступит k раз в n опытах, равна коэффициен ту
при x k многочлена
n ( x) (q1 p1 x)( q2 p2 x) (qn pn x),
где n ( x) производящ ая функция .

9.

Если в каждом испытании может произойти
одно и только одно из m событий A1 , A2 , , Am ,
испытания независимы и в каждом из них событие Ai
происходит с вероятостью pi (i 1, m), то вероятность
того, что в n независимых испытаниях появятся
k1 событий A1 , k 2 событий A2 , , k m событий Am , равна
n!
Pn (k1 , k 2 , , k m )
p1k1 p2k 2 pmk m ,
k1!k 2 ! k m !
где k1 k 2 k m n и p1 p2 pm 1.
(3)

10.

Легко также убедиться в том, что вероятность (3)
является коэффициен том при x1k1 x2k2 xmkm в разложении
полинома
( x1 , x2 , , xm ) ( p1 x1 p2 x2 pm xm ) n
по степеням x1 , x2 , , xm .
Вероятност и (3) называются полиномиальным
распределением.

11.

Пример. Экзаменаци онный тест состоит из 20 заданий.
В каждом задании имеется по 4 ответа, из них один верный.
При этом, оценка 2 (неуд.) ставится за ответ, содержащий
менее 8 правильных ответов, 3 ( удов.) от 8 до 14, 4 ( хор.)
от 15 до 18, 5 (отл.) 19 или 20. Найти вероятности получения
каждой оценки , если отвечать на вопросы теста наугад.
Воспользуе мся формулой (1). Тогда из условий задачи
следует
1
3
n 20, p , q 1 p ,
4
4
k
20!
1 3
P20 (k )
k!(20 k )! 4 4
20 k
20!
320 k
20 .
k!(20 k )! 4

12.

Вероятност ь получить оценку 2 (неуд.)
P (неуд.) P20 (0) P20 (1) P20 (2) P20 (3) P20 (4)
P20 (5) P20 (6) P20 (7) 0,898.
Вероятност ь получить оценку 3 ( удов.)
P ( удов.) P20 (8) P20 (9) P20 (10) P20 (11)
P20 (12) P20 (13) P20 (14) 0,102.
Вероятност ь получить оценку 4 ( хор.)
P ( хор.) P20 (15) P20 (16) P20 (17) P20 (18) 3,8 10 6.
Вероятност ь получить оценку 5 (отл.)
P (отл.) P20 (19) P20 (20) 5,5 10 11.

13.

Определим наивероятнейшее число угаданных ответов :
1
1
(n 1) p 21 5
k0 5.
4
4
Предположим теперь, что среди вопросов имеются
такие, где ответом является некотый термин или число
(вводимые с клавиатуры). Будем считать, что угадать
ответы на такие вопросы невозможно. Тогда вероятности
оценок наугад сданного теста изменятся следующим образом.

14.

Оценки при 5 ти " безвариантных" вопросах.
P(неуд.) P15 (0) P15 (1) P15 (2) P15 (3) P15 (4)
P15 (5) P15 (6) P15 (7) 0,983.
P( удов.) P15 (8) P15 (9) P15 (10) P15 (11)
P15 (12) P15 (13) P15 (14) 0,017.
P( хор.) P15 (15) 9,3 10 10.
P(отл.) 0.
Наивероятн ейшее число угаданных ответов k0 4 и k0 1 3.

15.

Оценки при 10 ти " безвариантных" вопросах.
P (неуд.) P10 (0) P10 (1) P10 (2) P10 (3) P10 (4)
P10 (5) P10 (6) P10 (7) 0,99958.
P ( удов.) P10 (8) P10 (9) P10 (10) 0,00042.
P ( хор.) 0.
P (отл.) 0.
Наивероятн ейшее число угаданных ответов k0 2.

16.

Использование формулы Бернулли при больших
значениях n и k вызывает большие трудности, так как
это связано с громоздким и вычислениями. Вычисление
Pn (k ) вызывает затруднения также при малых
значениях p (или q). Возникает необходимость в
отыскании приближенных формул для вычисления Pn (k ),
обеспечивающих необходимую точность.

17.

Теорема. Если число испытаний неограничено
увеличивается (n ) и вероятность p наступления
события A в каждом испытании неограничено
уменьшается ( p 0), но так, что их произведение np
является постоянной величиной (np const ), то
вероятность Pn (k ) удовлетворяет предельному
равенству
k e
lim Pn (k )
.
n
k!
(4)
Выражение (4) называется асимптотич еской
формулой Пуассона.

18.

Из предельного равенства (4) при больших n и
малых p ( редкие события ) вытекает приближенная
формула Пуассона
k e
Pn (k )
, np, k 0, n.
k!
(5)

19.

Пример. Вероятност ь попадания в цель при каждом
выстреле равна 0,001. Найти вероятность попадания в
цель двумя и более пулями , если число выстрелов равно 5000.
Воспользуе мся формулой Пуассона (5). Тогда
np 5000 0,001 5
и искомая вероятность равна
5000
P5000 (k 2) P5000 (k ) 1 P5000 (0) P5000 (1)
k 2
50 e 5 51 e 5
1
1 6e 5 0,9596.
0!
1!

20.

Теорема ( Локальная теорема Муавра Лапласа ) .
Если вероятность p наступления события A в каждом
испытании постоянна и отлична от нуля и единицы, а
число независимых испытаний достаточно велико, то
вероятность Pn (k ) может быть вычислена по
приближенной формуле
1
Pn (k )
( x),
npq
(6)
где
k np
x
,
npq
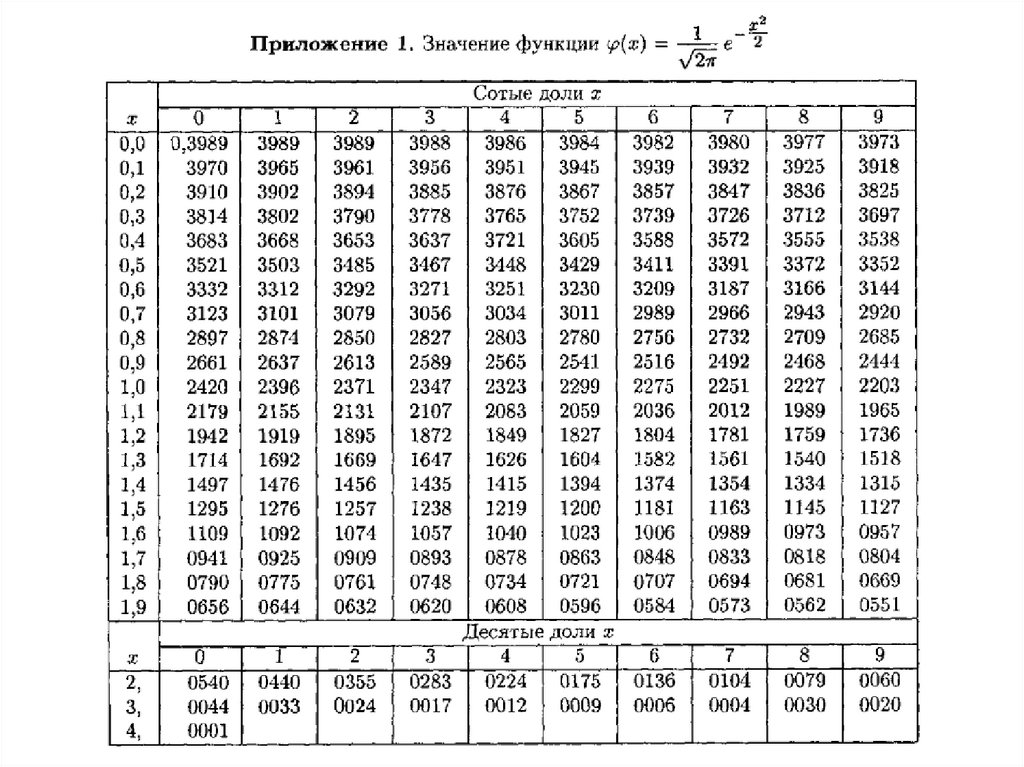
1
( x)
e
2
x2
2
функция Гаусса.

21.

22.

Пример. Вероятност ь попадания в мишень при одном
выстреле для данного стрелка равна 0,7. Найти вероятность
того, что при 200 выстрелах мишень будет поражена 160 раз.
Здесь : n 200, k 160, p 0,7, q 0,3. Применим
формулу (6). Имеем : npq 200 0,7 0,3 42 6,48,
160 200 0,7
20
3,1. Учитывая, что
6,48
42
(3,1) 0,0033, получаем
1
P200 (160)
0,0033 0,0005.
6,48
следовательно, x

23.

Теорема ( Интегральн ая теорема Муавра Лапласа ) .
Если вероятность p наступления события A в каждом
испытании постоянна и отлична от нуля и единицы, то
вероятность Pn (k1 , k 2 ) того, что событие A наступит в n
испытаниях от k1 до k 2 раз, может быть найдена по
приближенной формуле
x2
1
Pn (k1 , k 2 )
e
2 x1
z2
2
dz ( x2 ) ( x1 ),
(7 )
где
k1 np
k 2 np
1
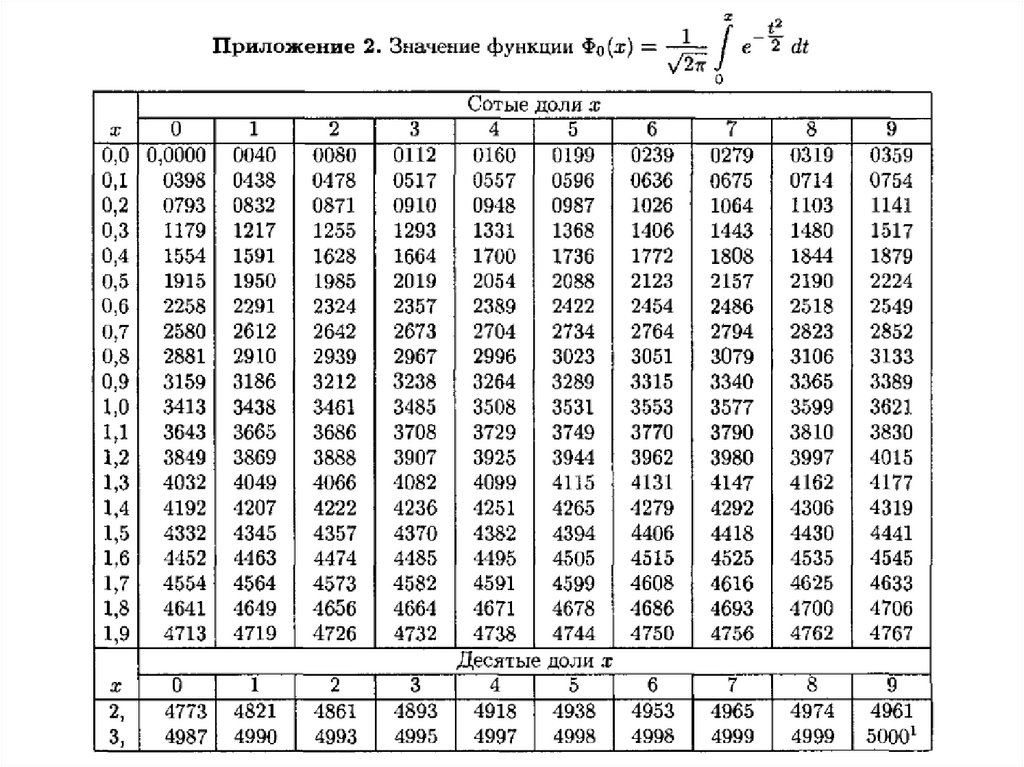
x1
, x2
, ( x)
e
npq
npq
2 0
x
z2
2
функция
dz
Лапласа.

24.

25.

Пример. Вероятност ь того, что деталь не прошла проверку
ОТК равна p 0,2. Найти вероятность того, что среди 400
случайно отобранных деталей окажется непроверенных от 70
до 100 деталей.
По условию, p 0,2, q 0,8, n 400, k1 70, k 2 100.
Воспользуе мся формулой (7) :
P400 (70,100) ( x2 ) ( x1 ).
Вычислим нижний x1 и верхний x2 пределы интегрирования :
100 400 0,2
70 400 0,2
2,5.
1,25, x2
x1
400 0,2 0,8
400 0,2 0,8
Таким образом, имеем
P400 (70,100) (2,5) ( 1,25) (2,5) (1,25)
0,4938 0,3944 0,8882.

26.

Спасибо за внимание!