Similar presentations:
Полная вероятность события. Формула Байеса переоценки гипотез. Повторные испытания Бернулли. Лекция 4
1.
Лекции по теориивероятностей
Белоусова Вероника Игоревна
к.ф.-м.н., доцент
2.
Полная вероятность события. Формула Байеса переоценкигипотез.
Повторные испытания Бернулли.
Вероятность повторных испытаний. Локальная и
интегральная теоремы Лапласа
3. План лекции
•Полная вероятность события.•Формула Байеса переоценки гипотез.
•Повторные испытания Бернулли.
•Вероятность повторных испытаний. Локальная и
интегральная теоремы Лапласа
4. Полная вероятность события
Определение. Пусть событие А может произойтитолько совместно с одним из событий Н1, Н2,…,
Нп, образующих полную группу несовместных
событий.
Тогда события Н1, Н2,…, Нп называются
гипотезами.
5. Например
Событие А – презентация фильма прошлауспешно
H1 – судьи состояли из детей
Н2 – судьи из взрослых
Н3 – смешанное судейство
6. Вероятность события А
Когда наступает событие А?Н1
И
или
Н2
И
или
А
И
…
Hi или
И
Нn
7. Теорема.
Вероятность события А, наступающего совместно сгипотезами Н1, Н2,…, Нп, равна:
n
р ( А) p ( H i ) p ( A / H i ),
i 1
где p(Hi) – вероятность i- й гипотезы,
а p(A/Hi) – вероятность события А при условии
реализации этой гипотезы.
Формула называется формулой полной вероятности.
8. доказательство
Можно считать событие А суммой попарнонесовместных событий АН1, АН2,…, АНп.
Тогда из теорем сложения и умножения следует, что
P( A) P AH1 AH 2
P( A) P AH1 P AH 2
AH n
P AH n
n
P H i P A / H i .
i 1
что и требовалось доказать.
9. Пример
Имеется 2 урны с шарами.В первой из них 3 белых и 4 черных шара, во
второй – 2 белых и 5 черных. Из первой урны
случайно выбирают шар и перекладывают во
вторую.
Найти вероятность того, что вытащенный затем
наудачу шар из второй урны белый.
10.
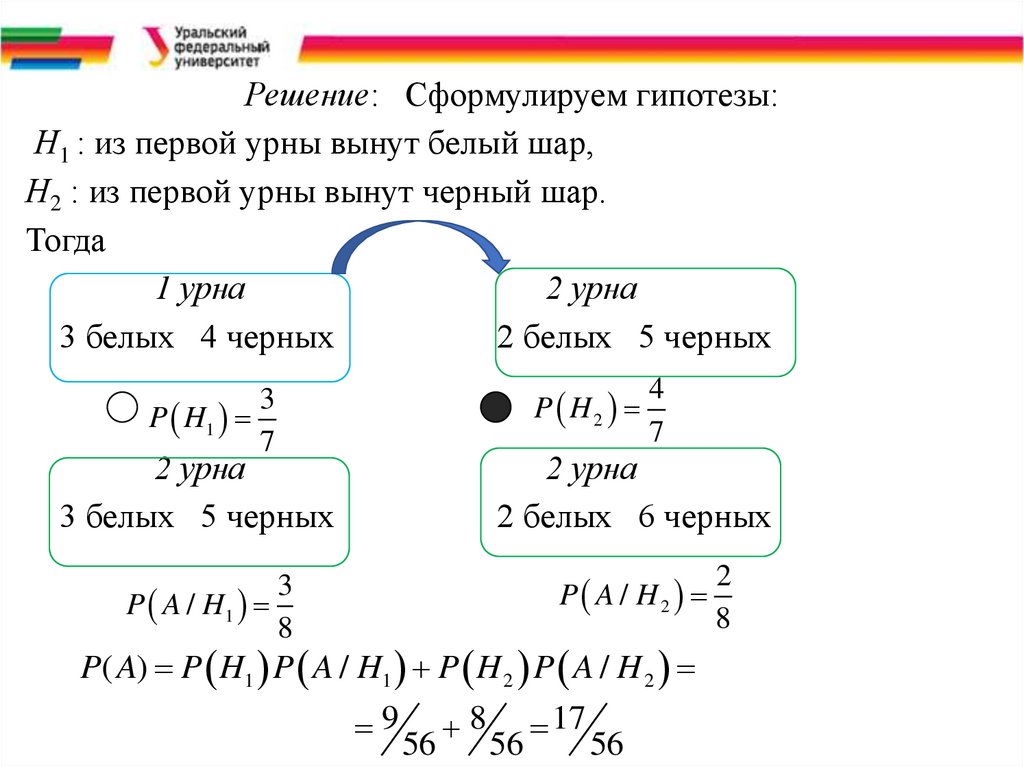
Решение: Сформулируем гипотезы:Н1 : из первой урны вынут белый шар,
Н2 : из первой урны вынут черный шар.
Тогда
1 урна
2 урна
3 белых 4 черных
2 белых 5 черных
P H2
3
P H1
7
4
7
2 урна
3 белых 5 черных
2 урна
2 белых 6 черных
3
P A / H1
8
2
P A / H2
8
P( A) P H1 P A / H1 P H 2 P A / H 2
9
56
8
56
17
56
11. Переоценка гипотез
• Пусть известен результат опыта, а именно то, чтопроизошло событие А.
• Этот факт может изменить априорные (то есть
известные до опыта) вероятности гипотез.
• Вопрос: Чему равна вероятность того, что к
возникновению события привело появление
определенной гипотезы р ( Н i / A) ?
12. Вероятность события
• В какую формулу входит условная вероятностьр ( Н i / A) ?
• Условная вероятность р ( Н i / A) входит в
формулу теоремы умножения вероятностей:
p( A H i ) p( A) p( H i / A) p( H i ) p( A / H i ),
13. Формула Байеса (теорема гипотез).
Из формулыp( A H i ) p( H i ) p( A / H i )
выразим p ( H i / A) :
Получим используемую для переоценки вероятностей гипотез при
известном результате опыта формулу Байеса:
p( H i ) p( A / H i )
р ( Н i / A)
.
p ( A)
14. Пример
После двух выстрелов двух стрелков, вероятности попаданий которых равны0,6 и 0,7, в мишени оказалась одна пробоина.
Найти вероятность того, что попал первый стрелок.
Решение:
Пусть событие А – одно попадание при двух выстрелах,
Н1 – первый попал, а второй промахнулся,
Н2 – первый промахнулся, а второй попал,
Н3 – оба попали,
Н4 – оба промахнулись.
15. Пример
Вероятности гипотез:р(Н1) = 0,6·0,3 = 0,18, (первый попал, а второй промахнулся)
р(Н2) = 0,4·0,7 = 0,28,
(первый промахнулся, а второй попал)
р(Н3) = 0,6·0,7 = 0,42,
(оба попали)
р(Н4) = 0,4·0,3 = 0,12. (оба промахнулись)
Тогда р(А/Н1) = р(А/Н2) = 1,
р(А/Н3) = р(А/Н4) = 0.
р(А) = 0,18·1 + 0,28·1 + 0,42·0 + 0,12·0 = 0,46.
0,18 1
9
Применяя формулу Байеса, получим: р( Н 1 / А) 0,46 23 0,391.
16. Схема Бернулли повторения испытаний
Рассмотрим серию из n испытаний, в каждомиз которых событие А появляется с одной и той же
вероятностью р, причем результат каждого
испытания не зависит от результатов остальных.
Подобная постановка задачи называется
схемой повторения испытаний.
17. Схема повторения испытаний. Формула Бернулли
Найдем вероятность того, что в такой сериисобытие А произойдет ровно к раз (неважно, в
какой последовательности).
Событие A - сумма равновероятных несовместных
событий, заключающихся в том, что:
1) из n выбраны k таких испытаний, при
которых:
2) А произошло в этих k испытаниях
и
3) не произошло в остальных (n-k) испытаниях.
18. Формула Бернулли
1. Число таких событий равно числу сочетаний С nиз n по k ,
2. Вероятность каждого из испытаний равна:
pkqn-k,
где q = 1 – p – вероятность того, что в данном опыте А
не произошло.
Применяя теорему сложения для несовместных
событий, получим формулу Бернулли:
k
p n (k ) C nk p k q n k
19. Якоб Бернулли
6 января 1655 16 августа 1705,швейцарский математик, один
из создателей теории
вероятностей.
20. Пример 1
Для получения приза нужно собрать 5 изделийс особым знаком на этикетке. Найти вероятность
того, что придется купить 10 изделий, если
этикетки с этим знаком имеют 5% изделий.
Решение:
21. Пример 1
Для получения приза нужно собрать 5 изделийс особым знаком на этикетке. Найти вероятность
того, что придется купить 10 изделий, если
этикетки с этим знаком имеют 5% изделий.
Решение:
Из постановки задачи следует, что последнее
купленное изделие имеет особый знак.
Следовательно, из предыдущих девяти эти знаки
имели 4 изделия.
22. Пример 1
Мы ищем вероятность события А:Последнее изделие было с особым знаком
и
4 и 9 из предыдущих тоже были с особым знаком.
Найдем вероятность второго условия по формуле
Бернулли: p (4) C 4 (0,05) 4 (0,95) 5 0,0006092.
9
9
Тогда Р(А) = 0,0006092 · 0,05 = 0,0000304.
23. Пример 2
Что вероятнее, выиграть у равносильного соперника неменее 3 партий из 4 или не менее 5 из 8?
24. Пример 2
Что вероятнее, выиграть у равносильного соперника неменее 3 партий из 4 или не менее 5 из 8?
Решение:
А- выиграть у равносильного соперника не менее 3 партий из 4
В- выиграть у равносильного соперника не менее 5 из 8
P( A) C43 (0,5) 4 C44 (0,5) 4 (0,5) 4 5 5
P ( B ) (0,5)8 C85 C86 C87 C88
(0,5)8 56 28 8 1 93
P B
93 16
93
1
P A 16 16 5 80
256
16
25. Пример 3
Проводится 10 испытаний по схеме Бернулли свероятностью успеха p и неудачи q. Найти вероятность
того, что успех произойдет только в двух случаях, при
этом между ними 3 раза испытание будет неуспешным.
Решение:
26. Когда формула Бернулли неудобна?
27. Приближение Пуассона для схемы Бернулли
При повторении испытаний равновозможные исходы испытания будутнаступать в среднем одинаково часто.
Пусть при большом числе испытаний вероятность появления А в одном
опыте мала, а произведение nр = λ сохраняет постоянное значение для
разных серий опытов
( то есть среднее число появлений события А в разных сериях испытаний
остается неизменным).
28. Приближение Пуассона для схемы Бернулли
Из nр = λ следует р = λ/n . Применим формулу Бернулли:Найдем предел полученного выражения при
29. Формула Пуассона
Таким образом, получена формула Пуассонакоторая позволяет найти вероятность к появлений события А для массовых
(n велико) и редких (р мало) событий.
Достаточно условий p<0,1 и npq<10
30. Симеон Дени Пуассон
французский математик, механик и физик.( 1781 г. — 1840 г.)
31. пример
Вероятность сбоя в системе при переключении еережимов равна 0,001. Найти вероятность того, что в
5000 переключениях будет не меньше двух сбоев.
32. пример
Вероятность сбоя в системе при переключении еережимов равна 0,001. Найти вероятность того, что в
5000 переключениях будет не меньше двух сбоев.
Решение
А – в 5000 переключениях будет от 2 до 5000 сбоев.
- в 5000 переключениях будет 0 или 1 сбой.
А
p=0,001 q=0,999 n=5000
npq=4,995<10
λ=np=5
50 5
P5000 (0) e 0,0067
0!
51 5
P5000 (1) e 5 0,0067
1!
P5000 (0) P5000 (1) 0,04
33.
Наивероятнейшее число появлений событияНаивероятнейшим числом появления события в
независимых испытаниях называется такое число ,
вероятность которого превышает или, по крайней
мере, не меньше вероятности каждого из остальных
возможных чисел появления события .
Обозначим Pm0 ,n вероятность,
наивероятнейшему числу m0.
соответствующую
34.
Наивероятнейшее число появлений событияИспользуя формулу, p n ( k ) C nk p k q n k
получим:
n!
m
m
n m
Pm ,n Cn p q
p m q n m
m0 ! n m0 !
0
0
0
0
0
0
Согласно определению наивероятнейшего числа,
вероятности наступления события А соответственно
m0-1 и m0+1 раз должны, по крайней мере не
превышать Pm0,n:
Pm 1,n Pm ,n
0
0
Pm 1,n Pm ,n
0
0
35.
Сначала распишем неравенствоPm 1,n Pm ,n
0
0
36.
Наивероятнейшее число появлений событияДля определения наивероятнейшего числа событий
в повторных испытаниях используют формулу:
np q m0 np p
Длина интервала, определяемого неравенством равна
единице, т. е.
np p np q p q 1.
37.
Наивероятнейшее число появлений событияnp q m0 np p
Событие может произойти в испытаниях только целое число
раз, то следует иметь в виду, что:
38.
Вероятность наивероятнейшего числа появлений событияПри больших значениях n пользоваться формулой
Бернулли для расчета вероятности, соответствующей
наивероятнейшему числу, неудобно. Если в формулу
Бернулли подставить формулу Стирлинга
n ! n n e n 2 n ,
и принять m0=np, то получим
формулу вероятности наступления
наивероятнейшего числа появления события А:
Pm ,n
0
1
2 npq
.
39.
ПримерИзвестно, что 1/15 часть продукции, поставляемой заводом на
торговую базу, не удовлетворяет всем требованиям стандарта. На
базу была завезена партия изделий в количестве 250 шт. Найти
наивероятнейшее число изделий, удовлетворяющих требованиям
стандарта, и вычислить вероятность того, что в этой партии
окажется наивероятнейшее число изделий.
Решение:
По условию n=250 q=1/15, значит p=14/15.
np q m0 np p
14 1
14 14
250 m0 250
15 15
15 15
233,26 m0 234,26 m0 234.
Pm ,n
0
1
2 npq
0, 254.
40.
Локальная теорема ЛапласаЛокальная теорема Лапласа дает асимптотическую
формулу, которая позволяет приближенно найти
вероятность появления событий ровно m раз в n
испытаниях, если число испытаний достаточно
велико, а p и q не достаточно малы.
41.
Локальная теорема ЛапласаТеорема. Если вероятность p появления события
А в каждом испытании постоянна и отлична от 0 и
1, то вероятность Pn(m) того, что событие А
появится в n испытаниях ровно m раз,
приближенно равна (тем точнее, чем больше n)
значению функции
1 x 2
m np
Pn m
e ,x
.
2
npq
2
1 x 2
x
e
- функция табличная
2
2
42.
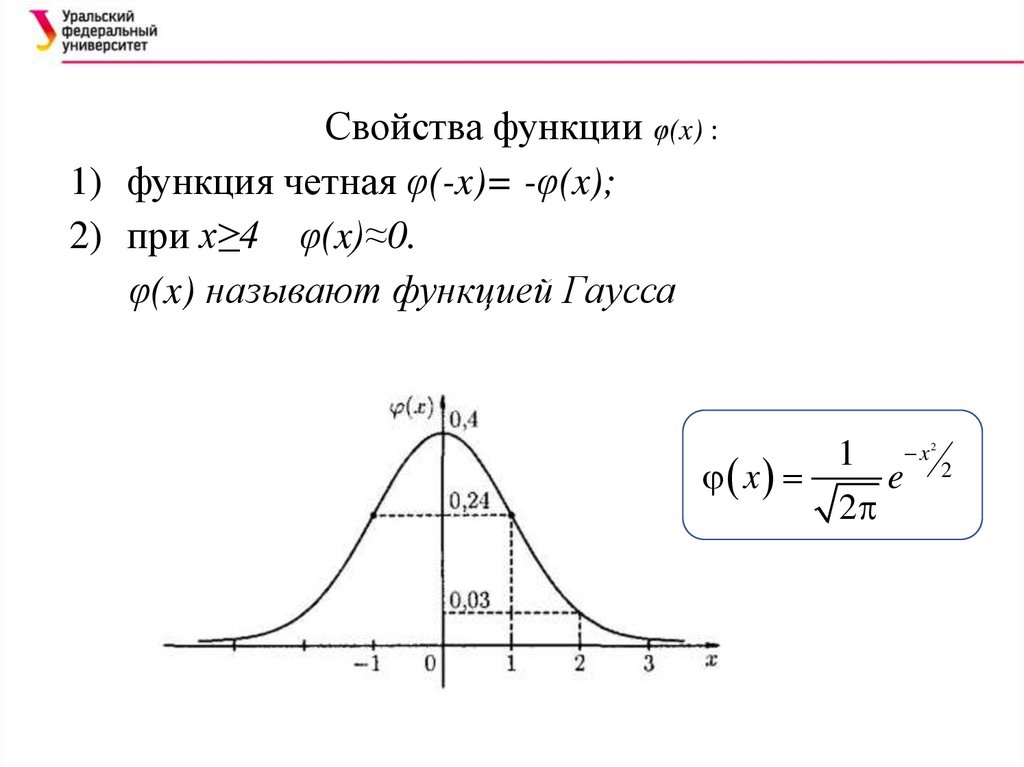
Свойства функции φ(x) :1) функция четная φ(-x)= -φ(x);
2) при x≥4 φ(x)≈0.
φ(x) называют функцией Гаусса
1 x 2
x
e
2
2
43.
ПримерНайти вероятность того, что событие наступит ровно 80 раз в
400 испытаниях, если вероятность появления события в
каждом испытании равна 0,2.
Решение. По условию n=400, m=80, p=0,2, q=0,8 (npq=64).
Применим асимптотическую формулу Лапласа.
1
1
P400 (80)
x x .
8
400 0, 2 0,8
44.
Интегральная теорема ЛапласаПусть в n независимых испытаниях, в каждом из
которых вероятность появления события А постоянна,
равна p и отлична от 0 и 1,
необходимо вычислить вероятность Pn m1 , m2 того,
что А появится не менее m1 и не более m2 раз (от m1 до
m2 раз), тогда
применяют интегральную теорему Лапласа.
45.
Интегральная теорема ЛапласаТеорема. Если вероятность наступления события
А постоянна и отлична от 0 и 1, то приближенно
вероятность Pn m1 , m2 появления события А от
m1 до m2 раз равна
x x 2
1
Pn m1 , m2
e
2 x
2
dx,
m1 np
m2 np
где x
, x
.
npq
npq
46.
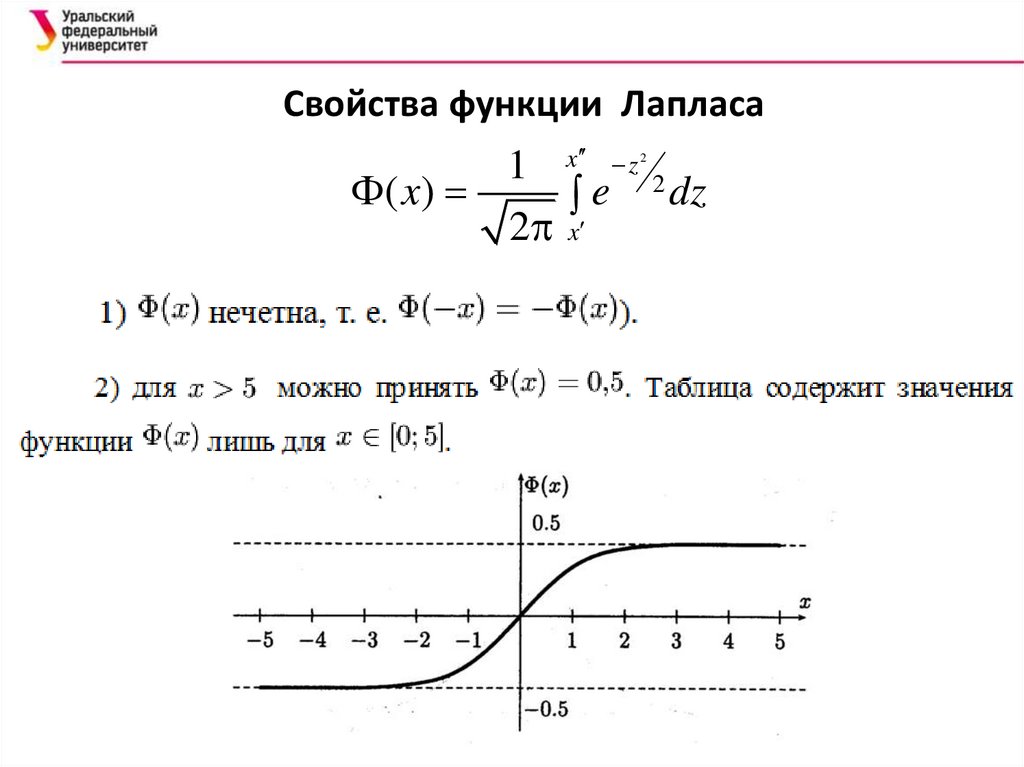
Функция Лапласа47.
Свойства функции Лапласа1 x z 2
( x)
e dz
2 x
2



















































 mathematics
mathematics








