Similar presentations:
Повторные независимые испытания
1. Повторные независимые испытания
Если производится несколько испытаний, причемвероятность наступления события А в каждом испытании
не зависит от исходов других испытаний, то такие
испытания называются независимыми относительно
события А.
Пусть при некотором испытании вероятность появления
события А равна р.
Пусть производится n таких испытаний, вероятность
появления события А в каждом испытании одна и та же: p.
2. Поставим задачу:
• Найти Pn (m) вероятность того, что среди nиспытаний событие А появится ровно m раз.
• Пример 1. Бросается монета. Событие А –
выпадение герба. P10 (3) среди 10-ти бросаний
герб выпадет 3 раза.
• Пример 2. Производится выстрел по мишени.
Событие А – мишень поражена.
P100 (35) вероятность поражения мишени
35 раз из 100 выстрелов.
3. Формула Бернулли. Формула Бернулли названа в честь выдающегося швейцарского математика Якоба Бернулли. Я. Бернулли (1654 –
1705) – профессорматематики Базельского университета, один из основателей теории
вероятностей и математического анализа.
4. Вывод формулы Бернулли.
В каждом испытании событие А может появиться свероятностью p и не появиться с вероятностью q=1-p.
Pn (m) ?
Если n=2, а m=1
и события: A1 - появление А в первом опыте,
A1 не появление А в первом опыте,
A 2 появление А во втором опыте,
A 2 не появление А во втором опыте, то
B A1 A2 A1 A 2
Событие В состоит в том, что А появилось 1 раз в 2-х
опытах.
.
5. Если n=3, а m=1,
и события: A1 появление А в первом опыте,A1 не появление А в первом опыте,
A 2 появление А во втором опыте,
A 2 не появление А во втором опыте,
A 3 появление А в третьем опыте,
A 3 не появление А в третьем опыте, то
событие B1 : А появилось 1 раз в трех опытах
будет:
B1 A1 A 2 A3 A1 A 2 A3 A1 A 2 A3 .
6. Если n = 3, m=2
событие B2 : А появилось 2 раза в трех опытахбудет:
B2 A1 A 2 A3 A1 A 2 A 3 A1 A 2 A 3 .
7. В общем случае для события : А появилось m раз в n опытах обозначим:
В общем случае для события Bm : А появилосьm раз в n опытах обозначим:
A1
появление А в первом опыте,
A1
не появление А в первом опыте,
A2
появление А во втором опыте,
A 2 не появление А во втором опыте,
.........................
A n появление А в n - ом опыте,
A n не появление А в n - ом опыте,
8.
B m A1 A 2 A3 A m A m 1 A nA1 A 2 A3 A m A m 1 A m 2 A n
A1 A 2 A3 A n m A n m 1 A m 2 A n .
9. В этой сумме слагаемых столько, сколькими способами можно из n опытов выбрать m, т.е.
mn
C .
10. Следовательно,
P(Bm ) Pn (m) P(A A A A A A1
2
3
m
m 1
n
A1 A 2 A3 A m A m 1 A m 2 A n
A1 A 2 A3 A n m A n m 1 A m 2 A n )
11. или
p qm
n m
p q
m
n m
p q
m
n m
m m
n m
C
p
q
.
n
m m
n m
Pn (m) C n p q .
12. Пример.
• Какова вероятность, что в трех испытаниях событиеА наступит два раза, если вероятность наступления
события А в каждом испытании равна 0,4 ?
Решение.
P3 (2) C (0,4) (0,6)
2
3
2
3 2
3 2
0,16 0,6 0,288.
1 2
13. Если требуется узнать, что в n испытаниях событие А наступит:
• 1). Не более к раз: Pn (m k ) Pn (0) Pn (1) Pn (2) Pn (k ).• 2). Более к раз: Pn (m k) Pn (k 1) Pn (k 2) Pn (k 3) Pn (n).
Pn (m k) Pn (m k) 1.
• 3). Не менее к раз:
Pn (m k) Pn (k) Pn (k 1) Pn (k 2) Pn (n).
• 4). Менее к раз:
Pn (m k) Pn (0) Pn (1) Pn (2) Pn (k 1).
Pn (m k) Pn (m k) 1.
14. Локальная формула Лапласа.
15. Лаплас (1749-1827) – выдающийся французский математик, физик и астроном, известен работами по небесной механике,
дифференциальнымуравнениям, один из создателей теории вероятностей.
Пусть производится n испытаний, в каждом из которых
вероятность появления события А равна р (0<p<1).
Т.е. P(A) p, P(A) q,
(p + q = 1).
n велико. Тогда вероятность наступления события
А m раз в n испытаниях равна:
1
Pn (m)
( x ),
npq
16.
• где1
( x )
2
x2
e 2 ,
m np
x
.
npq
Эта формула тем точнее, чем больше n
• (это асимптотическая формула).
• Составлены таблицы для ( x ) .
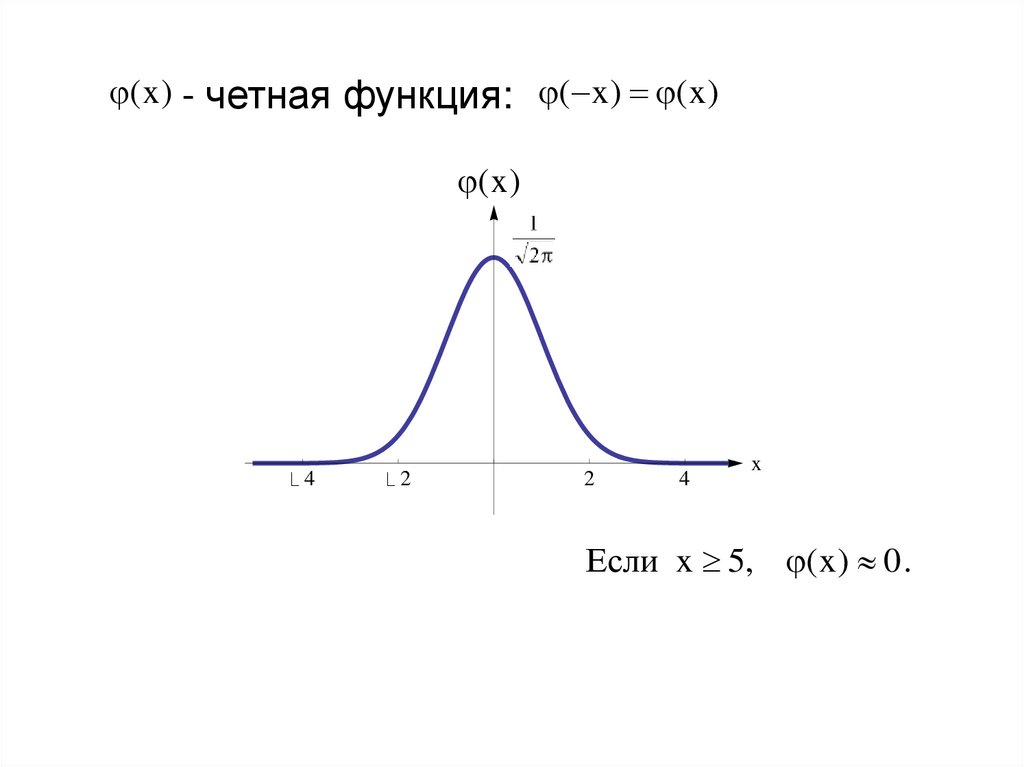
17. - четная функция:
( x ) - четная функция: ( x ) ( x )( x )
4
2
2
4
x
Если x 5, ( x ) 0 .
18. Пример.
• Найти вероятность того, что событие А наступит ровно 80раз в 400 испытаниях, если в каждом испытании
вероятность появления события А равна 0,2.
Решение.
n = 400; m = 80; p = 0,2 ; q = 1 – p = 1 – 0,2 = 0,8
m np 80 400 0,2
x
0 ; (0) 0,3989
npq
400 0,2 0,8
( (0) нашли по таблице).
P400 (80)
Тогда
1
0,3989 0,0491.
400 0,2 0,8
19. Интегральная формула Лапласа.
• Ищем вероятность того, что в n повторных независимыхиспытаниях событие А появится не менее m1 и не более
m 2 раз. Вероятность появления события А в каждом
испытании одинакова и равна р.
Т.е. надо найти: Pn (m1 m m 2 ).
Тогда
Pn (m1 m m 2 ) ( x 2 ) ( x1 ),
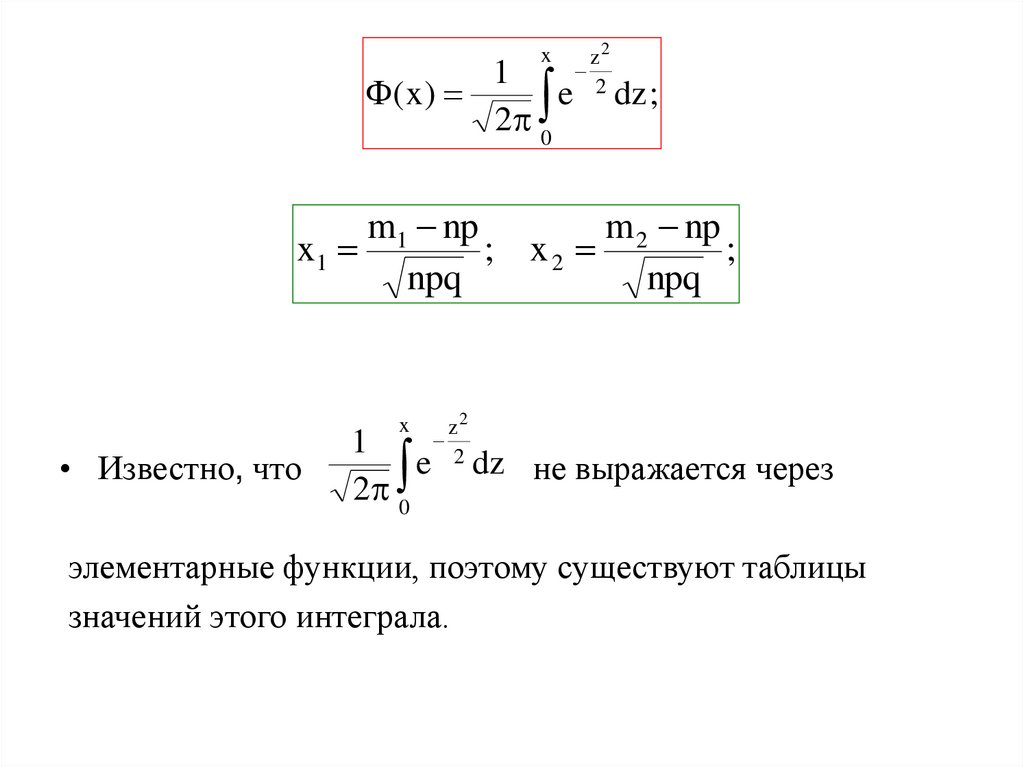
20.
x1
( x )
2 0
z2
e 2 dz ;
m1 np
m 2 np
x1
; x2
;
npq
npq
x
• Известно, что
1
2 0
z2
e 2 dz
не выражается через
элементарные функции, поэтому существуют таблицы
значений этого интеграла.
21.
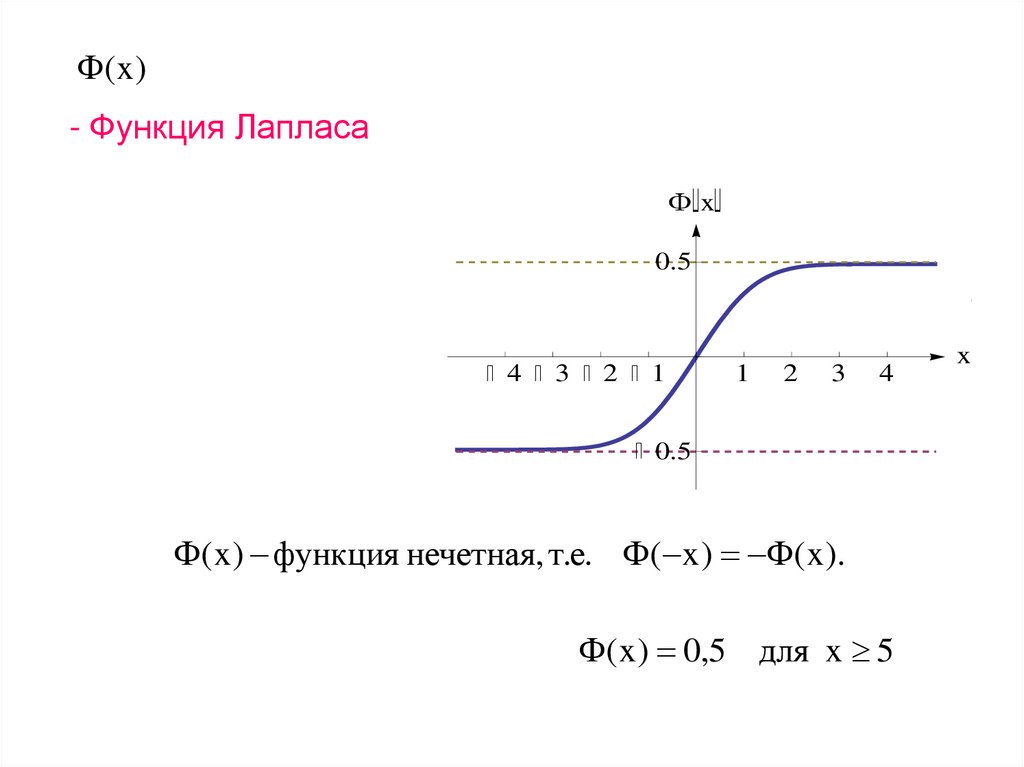
( x )- Функция Лапласа
Фx
0.5
( x ) функция нечетная, т.е. ( x ) ( x )
4
3
2
1
1
2
3
4
0.5
( x ) функция нечетная, т.е. ( x ) ( x ).
( x ) 0,5 для x 5
x
22. Формула Пуассона.
Пусть производится n испытаний, в каждом изкоторых вероятность появления события А равна
р.
Если n велико, то используем локальную формулу
Лапласа для определения вероятности наступления
события А m раз в n опытах. Но эта формула
непригодна, если вероятность события А в одном
опыте мала: p 0,1 .
В этом случае ( n – велико, р – мало и np 10 )
используют формулу Пуассона.
23. Пуассон (1781-1840) – знаменитый французский физик и математик.
24. Вывод формулы Пуассона.
n (n 1) (n m 1)m m n m
1
Pn (m) C n p q
1 2 m
n n
m
т.к. n имеет большое значение, вместо Pn (m)найдем
,
lim Pn (m).
n (n 1) (n m 1)
1
lim Pn (m) lim
1 2 m
n n
n
n
m
n m
n
n m
n
m
m
n n 1 n 2
n
m
1
1 1
lim
n n n n
n
n n
m!
25.
nm
m
1
2
m 1
lim 1 1 1 1
1 1
n n n
m! n n n
n
m
m
n
lim 1 lim 1
m! n n
m! n n
Pn (m)
e
m!
m
e
m!
m
- формула Пуассона.
26. Пуассоновский поток событий.
• Потоком событий называется последовательностьсобытий, которые наступают в случайные моменты
времени.
• Примеры: поступление вызовов на АТС, приход клиентов
на предприятие бытового обслуживания,
последовательность отказов элементов.
• Свойства потоков.
• Стационарность, отсутствие
последействия и ординарность.
27. Стационарность
• Свойство стационарности состоит в том, чтовероятность появления k событий на любом
промежутке времени зависит только от числа k и от
длительности промежутка и не зависит от начала его
отсчета.
• Т.е. вероятности появления k событий на
промежутках одинаковой длительности равны между
собой.
28. Свойство отсутствия последействия
• Свойство отсутствия последействия характеризуетсятем, что вероятность появления k событий на любом
промежутке времени не зависит от того, появлялись
или не появлялись события в моменты времени,
предшествующие началу рассматриваемого
промежутка.
• Т.е. предыстория потока не сказывается на
вероятности появления события в будущем.
29. Свойство ординарности
• Свойство ординарности характеризуется тем, чтопоявление двух и более событий за малый
промежуток времени практически невозможно.
30. Простейшим или пуассоновским потоком называется поток событий, который обладает свойствами стационарности, отсутствия
последействия и ординарности.• Интенсивностью потока называется
среднее число событий , которые появились
в единицу времени (площади, объема и т.д.)
Обозначим интенсивность потока 1.
31.
1 t среднее число событий за время t,и вероятность появления m событий за время t
определяется формулой Пуассона:
m
Pt ( m)
e
m!
- это математическая модель простейшего потока
событий.
32. Пример.
Среднее число вызовов, поступающих на АТС за однуминуту равно 2.
Найти вероятность того, что за 3,5 минуты поступит 5
вызовов. Поток вызовов предполагается простейшим.
Решение.
1 2; t 3,5; 1 t 7, m 5
m 7 5 7
P3,5 (5)
e e 0,1277.
m!
5!










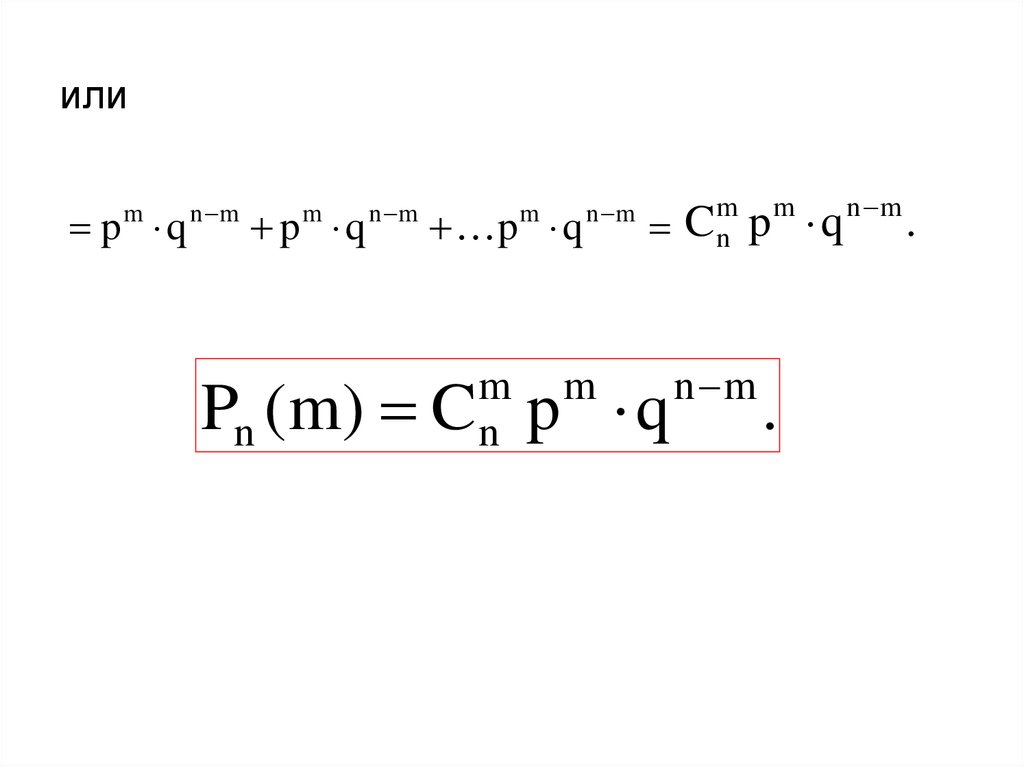


















 mathematics
mathematics








