Тема 3 Основ линейного программирования

1.

ОСНОВЫ
ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
1

2.

Линейное программирование – это разновидность
математического моделирования, частный случай
оптимального программирования.
Суть
принципа
стремлении
оптимальности
выбрать
такое
состоит
в
планово-
управленческое решение
2

3.

X x1, x2 ,..., xn
где
x j , j 1, n – его компоненты (параметры), которое
наилучшим образом учитывало бы внутренние возможности
и
внешние
условия
производственной
деятельности
хозяйствующего субъекта.
3

4.

Слова «наилучшим образом» здесь означают выбор
некоторого
некоторого
критерия
оптимальности,
экономического
т.
е.
показателя,
позволяющего сравнивать эффективность тех или
иных планово-управленческих решений.
4

5.

Традиционные
«максимум
критерии
прибыли»,
оптимальности:
«минимум
затрат»,
«максимум рентабельности» и др.
Таким
образом,
реализовать
на
практике
принцип оптимальности в планировании и
управлении
–
это
значит
решить
экстремальную задачу вида:
5

6.

max(min) f ( X )
(1)
X D
(2)
где f ( X ) - математическая запись
оптимальности – целевая функция
критерия
6

7.

D – область определения задачи. Совокупность
чисел X x1, x2 ,..., xn , удовлетворяющих
ограничениям задачи называется допустимым
решением (или планом).
Задачу условной оптимизации (1), (2) обычно
записывают в виде:
Найти максимум или минимум функции
f ( X ) = f x1, x2 ,..., xn
При ограничениях
(3)
7

8.

1 x1, x2 ,..., xn , , b1 ,
2 x1, x2 ,..., xn , , b2 ,
............................................
m x1, x2 ,..., xn , , bm ,
x j 0,
j 1, n
(4)
(5)
Условие (5) необязательно, но его всегда при
необходимости можно добиться.
8

9.

Обозначение , , говорит о том, что в конкретном
ограничении возможен один из знаков: , ,
Задача (3 – 5) – общая задача оптимального
(математического) программирования, иначе –
математическая модель задачи оптимального
программирования.
План X * x1* , x2* ,..., xn* , при котором целевая функция
задачи принимает максимальное (минимальное)
значение, называется оптимальным.
9

10.

В случае линейного программирования целевая
функция
f (X)
может быть представлена в виде
линейной формы
f ( X ) c1 x1 c2 x2 ... cn xn
c j заданные постоянные величины, а связь с
ограниченными ресурсами описывается
линейными уравнениями и неравенствами
10

11.

max(min) f x1, x2 ,..., xn ,
(6)
i x1, x2 ,..., xn , , bi , i 1, m ,
x j 0,
Наиболее
(8)
j 1, n,
изучены
задачи
линейного
для
которых
разработан
метод
решения
–
программирования,
универсальный
(7)
метод
последовательного улучшения плана (симплексметод)
11

12.

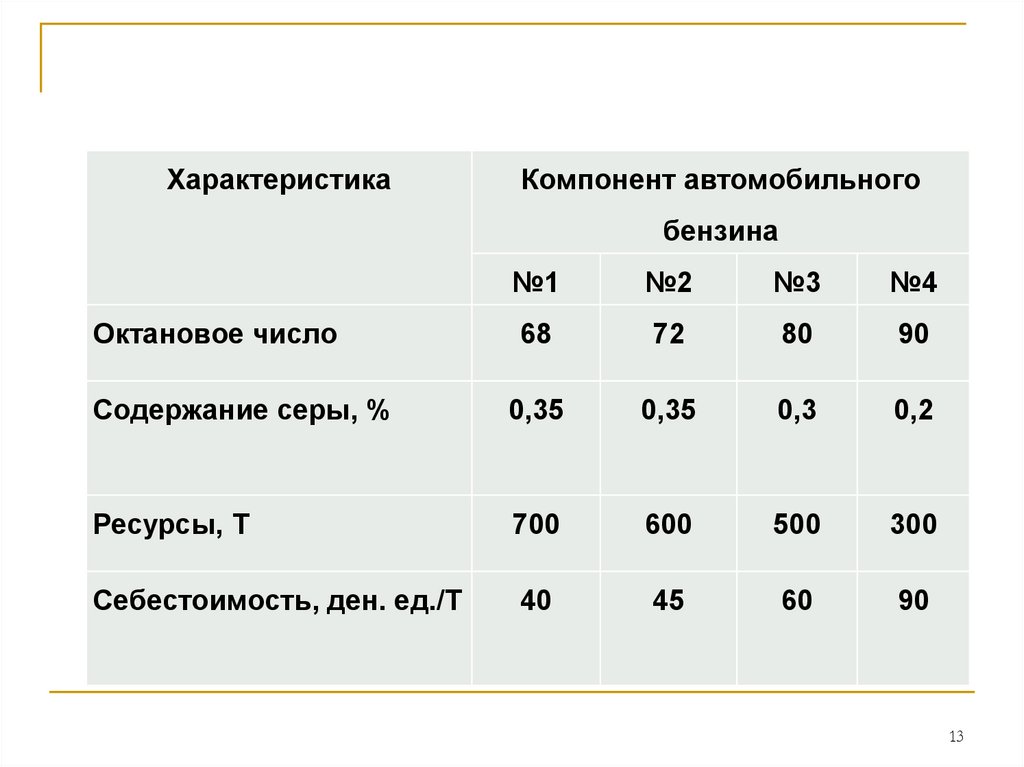
Пример 3. Задача о смесях.
Стандартом предусмотрено, что октановое число
автомобильного бензина А-76 должно быть не ниже
76, а содержание серы в нем – не более 0,3%. Для
изготовления такого бензина на заводе используется
смесь из четырех компонентов. Данные о ресурсах
смешиваемых компонентов, их себестоимости и их
октановом числе, а также о содержании серы
приведены в таблице.
12

13.

Характеристика
Компонент автомобильного
бензина
№1
№2
№3
№4
Октановое число
68
72
80
90
Содержание серы, %
0,35
0,35
0,3
0,2
Ресурсы, Т
700
600
500
300
Себестоимость, ден. ед./T
40
45
60
90
13

14.

Требуется определить, сколько тонн каждого
компонента следует использовать для получения
1000 т автомобильного бензина А-76, чтобы его
себестоимость была минимальной.
14

15.

Решение
Для
решения
этой
задачи
сформулируем
ее
экономико-математическую модель.
Введем необходимые обозначения:
пусть x j ( j 1,2,3,4) - количество в смеси компонента
с номером j. С учетом этих обозначений имеем
задачу (критерий оптимальности – «минимум
себестоимости»):
15

16.

min f ( X ) 40 x1 45 x2 60 x3 90 x4
x1 x2 x3 x4 1000 ,
(1)
68 x1 72x2 80 x3 90 x4 76 1000 ,
(2)
0, 35 x1 0, 35 x2 0, 3 x3 0, 2 x4 0, 3 1000 ,
(3)
x1 700,
x2 600,
x3 500,
x4 300,
x j 0, j 1, 2, 3,4
16

17.

Функциональное
ограничение
(1)
отражает
необходимость получения заданного количества
смеси (1000 т), (2), (3) – ограничения по
октановому числу и содержанию серы в смеси,
остальные – ограничения на имеющиеся объемы
соответствующих ресурсов.
17

18.

Полученная
математическая
задача-задача
линейного программирования. Она может быть
решена
симплекс-методом,
который
мы
рассмотрим позже.
В результате решения получается оптимальное
решение
X * x1* , x 2* , x 3* , x4* :
x1* 571т, x2* 0 т, x3* 143 т, x* 286 т,
4
18

19.

Подставляя найденное решение в целевую
функцию, имеем
f ( X * ) 40 571 45 0 60 143 90 286 57160 (ден. ед.)
Таким образом, оптимальному решению
X*
будет
отвечать минимальная себестоимость в 57160 ден.
ед.
19

20.

Решение систем алгебраических
линейных уравнений
Метод Крамера
20

21.

Рассмотрим систему из n линейных уравнений с n
неизвестными (определенная система)
a11 x1 a12 x2 ... a1n xn b1 ,
a x a x ... a x b ,
21 1
22 2
2n n
2
....................................................
an1 x1 an2 x2 ... ann xn bn
(1)
21

22.

Определитель
системы
,
составленный
из
коэффициентов при неизвестных, имеет вид
a11
...
an1
a12
...
an 2
... a1n
... ...
... ann
Числа b1 , b2 ,..., bn свободные члены.
Система (1) называется однородной, если
b1 b2 ... bn 0.
22

23.

Решением системы (1) называется совокупность
чисел x1 1 , x2 2 , ..., xn n ,
которые
обращают все уравнения в тождества.
Система
имеющая
хотя
бы
одно
решение,
называется совместной.
Система,
не
имеющая
решений,
называется
несовместной.
23

24.

Решить
систему
уравнений
(1)
можно
различными методами, в частности, методом
Крамера (Крамер – швейцарский математик,
1704 – 1752)
24

25.

Теорема Крамера
Если определитель системы (1) отличен от
нуля,
то
система
совместна
и
имеет
единственное решение, которое можно найти по
формуле:
xj
j
,
j 1, n
25

26.

В этой формуле
j является определителем,
полученным из определителя системы путем
замены столбца j столбцом свободных членов.
Замечание
Если определитель системы уравнений (1) = 0,
то система (1) или несовместна или имеет
бесконечно много решений.
26

27.

Пример
x y 1
Решить систему уравнений
x y 2
Решение
1 1
Определитель системы
1 1 2 0
1 1
Система имеет единственное решение.
27

28.

1 1
x
1 2 3,
2 1
1 1
y
2 1 1
1 2
x 3
x
1,5;
2
y
1
y
0, 5
2
ОТВЕТ: х = 1,5; у = 0,5
28

29.

Однородная система трех линейных
уравнений
Для простоты полагаем n = 3
Однородная система
a11 x1 a12 x2 a13 x3 0
a21 x1 a22 x2 a23 x3 0
a x a x a x 0
31 1
32 2
33 3
(1)
29

30.

Система (1) имеет тривиальное решение:
x1 0, x2 0, x3 0,
но может случиться, что однородная система (1)
имеет и не нулевое решение. Его называют
нетривиальным решением однородной системы (1).
30

31.

Теорема
Линейная однородная система трех линейных
уравнений с 3 неизвестными имеет ненулевое
решение
тогда
и
только
тогда,
когда
ее
определитель = 0, т. е.
a11 a12
a 21 a 22
a 31 a 32
a13
a 23 0
a 33
31

32.

Доказательство
Пусть система (1) имеет ненулевое решение x1 , x2 , x3
Пусть ее определитель 0, тогда на основании
формул Крамера система (1) имеет только нулевое
решение
x1
x 3
x1
x 2
, x2
, x3
x1 x2 x3 0, т.к.
b1 b2 b3 0
32

33.

Это
противоречит
предположению.
Следовательно, = 0. Тогда линейная система (1)
либо несовместна, либо имеет бесконечно много
решений. Но наша система совместна, так как
имеется
нулевое
решение.
Следовательно,
система (1) допускает бесконечно много решений,
в том числе и ненулевые.
33

34.

Пример
Решить систему уравнений
3 x 2 y z 0
2 x y 3z 0
x y z 0
3 2 1
1 3
2 3
2 1
2 1 3 3
2
1
1 1
1 1
1 1
1 1 1
3( 2) 2( 2 3) (2 1) 6 10 3 1 0
34

35.

Система имеет тривиальное решение: x y z 0
Другой способ расчета:
0
0 1
11 5
11 5
3
1
2 1
2 1 1
ОТВЕТ: (0, 0, 0)
35

36.

ОБРАТНАЯ МАТРИЦА.
РЕШЕНИЕ МАТРИЧНЫХ
УРАВНЕНИЙ
36

37.

Определение
Если определитель A матрицы А равен нулю, то
матрица А называется вырожденной; в противном
случае матрица А называется невырожденной.
37

38.

Рассмотрим теперь так называемую обратную
матрицу, понятие которой вводится только для
квадратной матрицы.
Определение
Если А – квадратная матрица, то обратной для нее
матрицей называется матрица, обозначенная А-1 и
удовлетворяющая условиям
1
AA 1 E , A A E , где Е – единичная матрица
38

39.

Определение
a11
a21
Пусть дана матрица A
...
an1
a12
a22
...
an 2
... a1n
... a2 n
... ...
... ann
~
Составим матрицу A из алгебраических дополнений
к элементам транспонированной матрицы AT :
39

40.

A11
~ A12
A
...
A1n
A21
A22
...
A2 n
... An1
... An2
... ...
... Ann
~
Матрица A называется матрицей, присоединенной
к матрице А.
40

41.

Теорема
Если матрица А не вырожденная, то она имеет
обратную матрицу,
A 1
которая находится по
формуле
A
1
1 ~
A,
или
A
1
1 ~
A
A
~
где A
- матрица, присоединенная к матрице А,
41

42.

a11
a21
A
...
an1
На
основании
a12
a22
...
an2
... a1n
... a2 n
... ...
... ann
теоремы
запишем
алгоритм
получения обратной матрицы:
1. Находим определитель матрицы А:
Если A 0 , то обратная матрица не существует.
Если A 0 , то переходим ко 2 шагу.
42

43.

2. Находим алгебраические дополнения всех
элементов aik матрицы А и записываем новую
матрицу составленную из Aik (алгебраических
дополнений).
3. Транспонируем полученную матрицу (меняем
местами
столбцы
полученной
матрицы
со
~
A
строками), получаем присоединенную матрицу .
43

44.

1
~
4. Умножим полученную матрицу A на
A
A
1
1 ~
A
A
Пример
2 1
4 3
Найти матрицу, обратную матрице A
Решение
1. Находим определитель матрицы А:
2 1
A
6 4 10 0
4 3
44

45.

Следовательно, данная матрица А является
невырожденной и имеет обратную матрицу.
2. Найдем алгебраические дополнения каждого
элемента:
1 1
A11 ( 1)
A21 ( 1)
2 1
3 3,
A12 ( 1)1 2 4 4,
( 1) 1,
A22 ( 1) 2 2 2 2.
45

46.

3 4
Получим матрицу
алгебраических
1
дополнений
3.
Транспонируем
2
эту
матрицу,
получаем
~ 3 1
присоединенную матрицу A
.
4 2
1
1
4. Умножим полученную матрицу на
, т. е. на
A
10
A
1
1 3 1 0,3 0,1
10 4 2 0,4 0,2
46

47.

Проверим полученный результат:
AA
1
2 1 0,3 0,1 0,6 0,4 0,2 0,2
4 3 0,4 0,2 1,2 1,2 0,4 0,6
1 0
E
0 1
ОТВЕТ: A
1
0,3 0,1
0,4 0,2
47

48.

РЕШЕНИЕ МАТРИЧНЫХ
УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
48

49.

Пусть для простоты n = 3, имеем систему
линейных
уравнений
(определенная
система:
3 уравнения, 3 неизвестных):
a11 x1 a12 x2 a13 x3 b1 ,
a21 x1 a22 x2 a23 x3 b2 ,
a x a x a x b
31 1
32 2
33 3
3
(1)
49

50.

Числа aik коэффициенты системы, а числа bi
свободные члены, i = 1, 3, k = 1, 3.
Решением системы (1) называется совокупность
чисел x1 = 1, x2 = 2, x3 = 3, которые обращают
все уравнения системы в тождества.
50

51.

Введем матрицу коэффициентов
a11 a12
A a 21 a 22
a
31 a 32
a13
a 23 ,
a 33
Х - вектор-столбец из неизвестных, а В – векторстолбец свободных членов:
x1
X x 2 ,
x
3
b1
B b2 .
b
3
51

52.

Согласно правилу умножения матриц данную
систему (1) можно записать так:
a11 a12
a 21 a 22
a
31 a 32
a13 x1 b1
a 23 x 2 b2
a 33 x 3 b3
или
a11 x1 a12 x 2 a13 x 3 b1
AX a 21 x1 a 22 x 2 a 23 x 3 b2 B
a x a x a x b
31 1
32 2
33 3 3
52

53.

Используя
определение
равенства
матриц,
данную систему (1) можно записать в виде
матричного уравнение
АХ = В ,
(1)
Здесь в роли неизвестного выступает матрица Х.
Уравнение (2) решается следующим образом. Если
А – невырожденная матрица ( A 0), то можно
определить обратную матрицу А 1 .
53

54.

Умножая обе части уравнения (2) слева на А 1
А 1 АХ = А 1 В
используем сочетательный закон умножения:
(А 1 А )Х = А 1 В , но так как А 1 А = Е , то
получаем решение матричного уравнения (2) в
виде Х = А 1В.
54

55.

Итак, чтобы решить матричное уравнение, нужно
1. Найти обратную матрицу А 1
2. Найти произведение А 1 В = Х
3. Пользуясь определением равных матриц,
записать ответ.
55

56.

Задача
Дана система уравнений
3 x1 x2 0 x3 5
2 x1 x2 x3 0
2 x x 4 x 15
1
2
3
решить ее матричным способом.
56

57.

Решение
Запишем систему в матричной форме АХ = В:
3 1 0 x1 5
2 1 1 x 2 0
2 1 4 x 15
3
Решение системы Х = А 1В
1. Найдем обратную матрицу А 1
57

58.

3 1 0
1 1
2 1
3
A 2 1 1 3
( 1) ( 1)
1 4
2 4
2 1 4
3 5 10 5 0
Выпишем
все
алгебраические
дополнения
элементов матрицы А:
1 1 1
A11 ( 1)
1
5;
1 4
1 2 2
A12 ( 1)
2
1
10;
4
58

59.

1 3 2
A13 ( 1)
2
1
0;
1
43
0
A22 ( 1)
12;
2 4
A31 ( 1)
3 1 1
1
0
1;
1
A21 ( 1)
2 1 1
A23 ( 1)
5 3
0
4;
1 4
1
1;
2 1
2 3 3
0
A32 ( 1)
3;
2 1
A33 1.
59

60.

5 10 0
Запишем новую матрицу 4 12 1
1 3 1
Транспонируем ее:
5 4 1
~
A 10 12 3 присоединенная матрица
0 1
1
1 1
, запишем обратную матрицу
Учитывая, что
A 5
60

61.

1 0,8 0,2
5 4 1
1
1 ~
1
A
A 2 2,4 0,6 10 12 3
A
0 0,2 0,2 5 0 1 1
2. Находим произведение Х = А 1 В
1 0, 8
X 2 2,4
0 0, 2
0, 2 5 1 5 0,8 0 ( 0, 2) 15 2
0,6 0 2 5 2,4 0 ( 0,6 ) 15 1
0, 2 15 0 5 1 0 0, 2 15 3
5
61

62.

3. Итак,
x1 2
X x2 1 , х = 2, х = 1, х = 3.
1
2
3
x
3 3
ОТВЕТ: (2, 1, 3)
Замечание
Другой расчет:
10 2
25 15
5 4 1 5
1
1
1
X 10 12 3 0 50 45 5 1
5
15 5 15 5 15 3
1
0 1
62

63.

СИСТЕМА m ЛИНЕЙНЫХ
УРАВНЕНИЙ С n ПЕРЕМЕННЫМИ
63

64.

Рассмотрим
систему
переменными (при
m
линейных
с
n
m < n такие системы
называются неопределенными):
Число уравнений m не равно, вообще говоря,
числу неизвестных n.
64

65.

a11 x1 a12 x2 ... a1 j x j ... a1n xn b1 ,
a21 x1 a22 x2 ... a2 j x j ... a2 n xn b2 ,
.................................................................
ai1 x1 ai 2 x2 ... aij x j ... ain xn bi ,
...................................................................
am1 x1 am 2 x2 ... amj x j ... amn xn bm ,
(1)
или в краткой записи
n
aij x j bi ,
j 1
i 1, 2,..., m
65

66.

или в векторной записи:
A1 x1 A2 x2 ... An xn B,
где
a11
a12
a1n
a
a
a2n
21
22
A1
,
A2
, …, An
,
a mn
a m1
am 2
b1
b2
B
bm
соответствующие вектор-столбцы.
66

67.

Запишем расширенную матрицу этой системы в
виде: А1
А2
…
Аn
a11 a12 ... a1n
a21 a22 ... a2 n
Ap
...............................
am1 am 2 ... amn
B
b1
b2
...
bm
Элементарными преобразованиями системы (1)
(или матрицы Ар) называются следующие
преобразования:
67

68.

1) перестановка любых двух уравнений (строк);
2) умножение обеих частей одного из уравнений
на любое отличное от нуля число;
3) прибавление к обеим частям одного уравнения
соответствующих частей другого, умноженных
на любое число, отличное от нуля;
68

69.

4) вычеркивание нулевой строки (уравнения с
нулевыми коэффициентами и свободным
членом, равным 0):
0 x1 0 x2 ... 0 xn 0
Определение.
Системы
уравнений
вида
(1)
называются
эквивалентными (или равносильными), если они
имеют одно и то же множество решений.
69

70.

Можно
показать,
что
элементарные
преобразования
переводят
данную
систему
уравнений в эквивалентную систему.
При практическом решении системы линейных
уравнений методом Гаусса последовательно над
строками матрицы Ар выполняют элементарные
преобразования, так что некоторое неизвестное
исключается из всех уравнений, кроме одного, т. е.
в составе расширенной матрицы формируется
единичная матрица.
70

71.

МЕТОД
ГАУССА
71

72.

Рассмотрим решение системы m линейных
уравнений с n переменными:
a11 x1 a12 x2 ... a1n xn b1 ,
a x a x .... a x b ,
21 1 22 2
2n n
2
......................................................
am1 x1 am 2 x2 ... amn xn bm .
(1)
72

73.

Метод
Гаусса
–
метод
последовательного
исключения переменных – заключается в том, что
с
помощью
элементарных
преобразований
система уравнений приводится к равносильной
системе ступенчатого (или треугольного) вида, из
которой последовательно, начиная с последних
(по номеру) переменных, находятся все остальные
переменные.
73

74.

Предположим, что в системе (1) коэффициент при
переменной х1 в первом уравнении а11 0 (если
это не так, то перестановкой уравнений местами
добьемся того, что а11 0 ).
Шаг 1. Умножая первое уравнение на подходящие
a 31 …, am1
a 21
числа (а именно на
)
,
,
a11
a11
a11
74

75.

и
прибавляя
последовательно
полученные
уравнения соответственно ко второму, третьему,
…, m–му уравнению системы (1), исключим
переменную х1 из всех последующих уравнений,
начиная со второго.
75

76.

Получим
a11 x1 a12 x2 ... a1n xn b1 ,
(1)
(1)
(1)
a
x
...
a
x
b
22 2
2n n
2 ,
..........................................................
(1)
(1)
(1)
a
x
...
a
x
b
i2 2
in n
i ,
...........................................................
(1)
(1)
(1)
am
x
...
a
x
b
mn n
m ,
2 2
(2)
где буквами с верхним индексом (1) обозначены
новые коэффициенты, полученные после первого
шага.
76

77.

Шаг 2.
(1)
Предположим, что a22
0 (если не так, то
соответствующей перестановкой уравнений или
переменных с изменением их номеров добьемся
(1)
того, чтобы a22
0 . Умножая второе уравнение
a (1)
последовательно на подходящие числа 32
,
(
1
)
a
22
(1)
a42
(1)
a
,
m2
(1) …, (1) и прибавляя полученные
a22
a22
77

78.

уравнения соответственно к третьему, четвертому,
…,
m–му
уравнению
системы,
исключим
переменную х2 из всех последующих уравнений,
начиная с третьего.
Продолжая процесс последовательного исключения
переменных, после (r 1)-го шага получим систему
78

79.

a11 x1 a12 x2 ... a1r xr a1, r 1 xr 1 ... a1n xn b1 ,
(1)
a22
x2 ... a2(1r) xr a2(1, r) 1 xr 1 ... a2(1n) xn b2(1) ,
...............................................................................................
( r 1)
( r 1)
arr
xr ar( ,rr 11) xr 1 ... arn
xn br( r 1) ,
0 br( r 11) ,
.................
( r 1)
0 bm
(3)
79

80.

Число нуль в последних m–r уравнениях означает,
что их левые части имеют вид: 0 x1 0 x2 ... 0 xn
Если хотя бы одно из чисел br( r 11) , … , bm( r 1) не
равны нулю, то соответствующее равенство
противоречиво, и система (1) несовместна.
Таким образом, для любой совместной системы
числа br( r 11) , …, bm( r 1) в системе (3) равны нулю. В
этом случае m–r уравнений в системе (3) являются
80

81.

тождествами и их можно не принимать во
внимание при решении системы (1).
Очевидно, что после отбрасывания «лишних»
уравнений возможны два случая:
а) число уравнений системы (3) равно числу
переменных т. е. r = n (в этом случае система (3)
имеет треугольный вид);
81

82.

б)
б)
r n
(в этом случае система (3) имеет
ступенчатый вид).
Переход системы (1) к равносильной ей системе (3)
называется
прямым
ходом
нахождение
переменных
из
метода
Гаусса,
системы
а
–
(3)
обратным ходом.
82

83.

Преобразование
Гаусса
удобно
осуществляя
преобразования
уравнениями,
а
с
не
расширенной
проводить,
с
самими
матрицей
системы (1)
a11 a12 ... a1n
a21 a22 ... a2 n
Ap
...............................
am1 am 2 ... amn
b1
b2
...
bm
83

84.

Задача
Решить систему уравнений:
x1 2 x2 3 x3 2 x4 6,
2 x 4 x 2 x 3 x 18,
1
2
3
4
3 x1 2 x2 x3 2 x4 4,
2 x1 3 x2 2 x3 x4 8,
84

85.

Решение
Расширенная матрица системы имеет вид:
1
2
3
2
2 3
2
4 2 3
2 1
2
3
2
1
6
18
4
8
Шаг 1 Так как a11 0. То умножая первую строку
последовательно
на
числа
( 2),
( 3),
( 2)
прибавляя полученные строки соответственно ко
85
и

86.

второй, третьей, четвертой строкам, исключим
переменную х1 из всех строк, начиная со второй.
(1)
0 , поменяем
Заметив, что в новой матрице a22
местами вторую и третью строки:
1
0
0
0
2
0
4
7
3
2 6
8
1 6
10
8 14
4
5 20
1
0
̴
0
0
2
4
0
7
3
10
8
4
2
8
1
5
6
14
6
20
86

87.

(1)
Шаг 2 Так как теперь a22
4 0 , то умножая
вторую строку на 7 и прибавляя полученную
4
строку к четвертой, исключим переменную х2 из
всех строк, начиная с третьей:
2
1
0 4
0
0
0
0
3
2
10 8
8
1
13,5 9
6
14
6
4, 5
1
0
̴ 0
0
2
3
4 10
0
8
0
0
6
14
6
117 117
16
8
2
8
1
87

88.

( 2)
Шаг 3 Учитывая, что a33
8 , умножая третью
строку на
13,5 27
8
16
и прибавляя полученную
строку к четвертой исключим из нее переменную
х3.
Получим
уравнений
(см.
последнюю
матрицу)
систему
x1 2 x2 3 x3 2 x4 6,
4 x 10 x 8 x 14,
2
3
4
8 x3 x4 6
117
117
x4
,
16
8
88

89.

Откуда, используя обратный ход метода Гаусса,
найдем из четвертого уравнения х4 = 2;
из третьего
из второго
6 x4 6 2
x3
1;
8
8
14 8 x4 10 x3
x2
2 и
4
из первого уравнения x1 6 2 x4 3 x3 2 x2 1,
т. е. х1 = 1, х2 = 2, х3 = 1, х4 = 2
ОТВЕТ: (1; 2; 1; 2)
89