Similar presentations:
Использование методологии нечетких множеств при оценке исследовательских проектов
1. Использование методологии нечетких множеств при обосновании управленческих решений
1. Основные понятия теории нечётких множеств2. Операции над нечёткими числами
3. Интерпретация нечётких множеств: теория возможности
4. Оценка инновационных проектов на основе теории
нечетких множеств
5. Оценивание качественных показателей проекта при помощи нечётких
множеств
6. Ранжирование проектов в нечетком представлении
7.Задача формирования портфеля проектов
2. 1. Основные понятия теории нечётких множеств
3.
Нечёткие множества были определены Л.Заде в 1965 году, как формальный аппарат
для обработки высказываний естественного
языка.
4.
Зафиксируем произвольное множество X. Нечёткое множество A задаётсяпосредством функции принадлежности μA: X→[0,1]. Значение μA(x) есть
число, лежащее между 0 и 1, показывающее степень принадлежности
элемента x нечёткому множеству A. Равенство μA(x) =1 означает, что x
точно принадлежит множеству A; равенство μA(x) =0 говорит о том, что
x точно не принадлежит множеству A.
Для обычного множества Y X функция принадлежности имеет вид
0
,
x
Y
;
Y 1, x Y
и принимает в качестве значений только 0 и 1.
Нечёткие множества отличаются от обычных множеств тем, что
допускают промежуточные степени принадлежности, например, μA(x)
=0,5.
Далее мы будем предполагать, что нечёткое множество A нормировано, т.е.
существует такой элемент x, что μA(x) =1.
5.
Если A и B – два нечётких множества, тогда функциипринадлежности
A B ( x) max( A ( x), B ( x)),
A B ( x) min( A ( x), B ( x)),
A ( x) 1 A ( x).
по определению задают результат операций объединения
A B, пересечения A B и дополнения на нечётких
множествах.
6.
Для любого числа α , 0 < α ≤ 1 , α-срезом нечёткогомножества A называется подмножество
A ={x X μA(x) }.
1-срез называют ядром нечёткого множества A.
Заметим, что нечёткое множество однозначно
восстанавливается по своим срезам.
Когда X=R – множество вещественных чисел,
говорят о нечётких числах.
7.
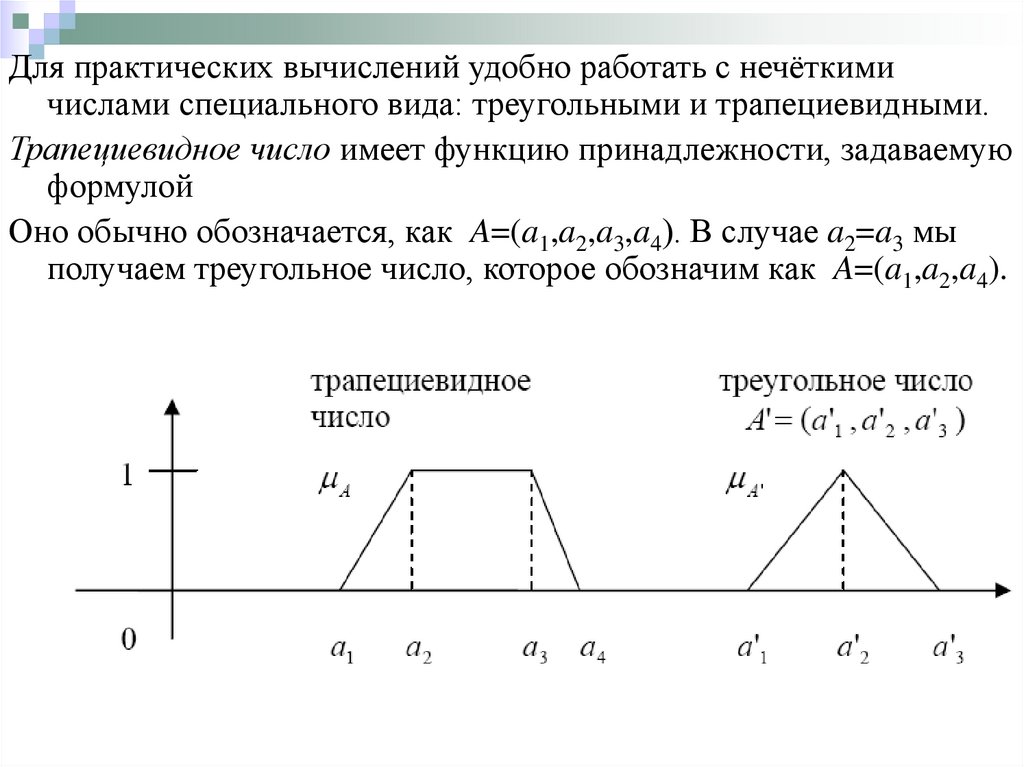
Для практических вычислений удобно работать с нечёткимичислами специального вида: треугольными и трапециевидными.
Трапециевидное число имеет функцию принадлежности, задаваемую
формулой
Оно обычно обозначается, как A=(a1,a2,a3,a4). В случае a2=a3 мы
получаем треугольное число, которое обозначим как A=(a1,a2,a4).
8. Функция принадлежности трапециевидного числа:
9. 2. Операции над нечёткими числами
10.
Нечёткие числа можно складывать, вычитать, умножать иделить, как и обычные числа. Применяя принцип
расширения к арифметическим операциям и
трапециевидным нечётким числам, мы получим следующие
правила сложения и вычитания:
(a1, a2, a3, a4) + (b1, b2, b3, b4)= (a1+ b1, a2+ b2, a3+ b3, a4+ b4),
(a1, a2, a3, a4) – (b1, b2, b3, b4)= (a1– b1, a2– b2, a3– b3, a4– b4).
Произведение и частное трапециевидных чисел уже не будут
трапециевидными, но будут криволинейно
трапециевидными. В данном случае можно написать
приближённые равенства:
(a1, a2, a3, a4) · (b1, b2, b3, b4) (a1 · b1, a2 · b2, a3 · b3, a4 · b4),
(a1, a2, a3, a4) / (b1, b2, b3, b4) (a1/ b4, a2/ b3, a3/ b2, a4/ b1).
Здесь предполагается, что нечёткие числа положительны, т.е.
ai 0, bi>0.
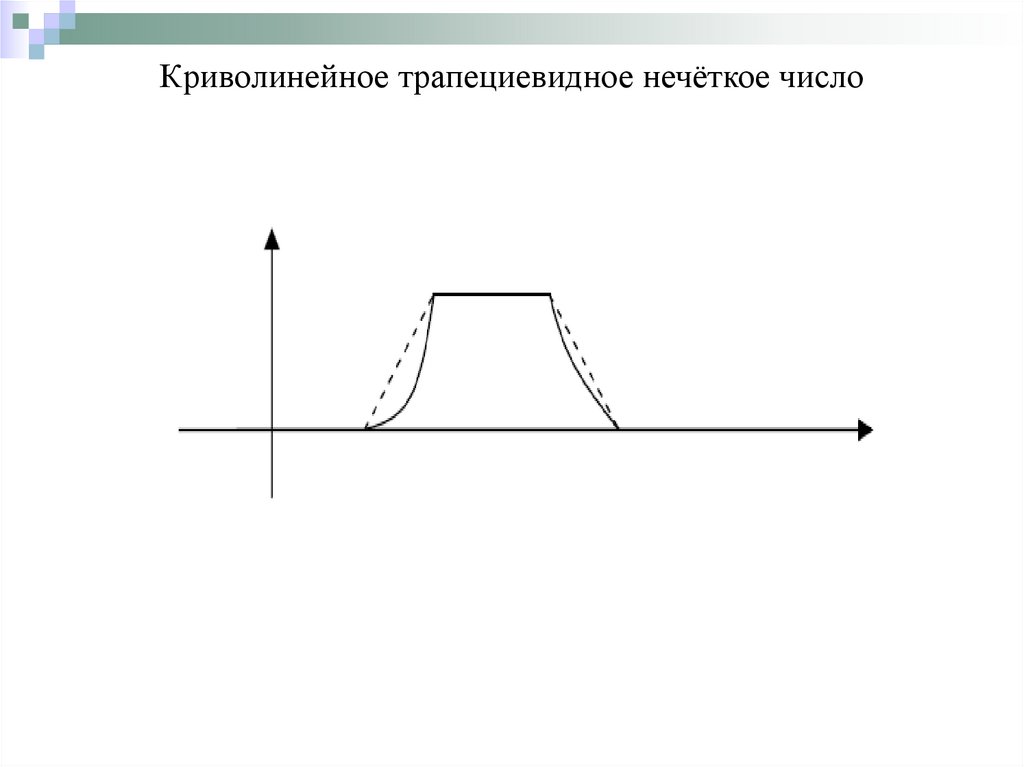
11. Криволинейное трапециевидное нечёткое число
12.
С нечётким трапециевидным числом A=(a1,a2,a3,a4) можносвязать две числовые характеристики: среднее значение
E(A)и дисперсию Var(A), вычисляемые по формулам.
a1 2a2 2a3 a4
E ( A)
,
6
(a4 a1 ) 2(a4 a1 )( a3 a2 ) 3(a3 a2 )
Var( A)
.
24
2
2
Данные формулы имеют место, если функцию
принадлежности интерпретировать как
(ненормированную) плотность вероятностного
распределения и рассмотреть математическое ожидание
и дисперсию соответствующей случайной величины.
13. 3. Интерпретация нечётких множеств: теория возможности
14.
Для того чтобы применение теории в приложенияхоказалось полезным, необходимо иметь
содержательную интерпретацию нечётких множеств и
нечётких чисел.
Пусть A – нечёткое число и μA – её функция
принадлежности. Тогда значение μA (x) показывает
правдоподобность того, что действительное значение
величины A равно x.
Л. Заде показал, что такая трактовка неопределённости,
связанной с нечётким числом, не является
вероятностной. Возникает новая теория, работающая с
неопределённостью, которую Заде назвал теорией
возможностей.
Таким образом, μA (x) показывает возможность того, что
нечёткая величина A принимает значение x.
15.
В рамках теории возможностей каждому событиюE сопоставляется определённое число Pos(E),
лежащее между 0 и 1,– возможность события.
Возможность удовлетворяет следующему
свойству для любых двух событий E1, E2:
16.
Таким образом, возможность события определяется возможностьюнаиболее благоприятного исхода для данного события. Формулу можно
обобщить на случай, когда Y – нечёткое множество с функцией
принадлежности μY(x) :
17.
Теория возможностей даёт средство для оценки нечёткихограничений. Пусть A –нечёткое число, B – нечёткое число,
представляющее некоторое ограничение. Фиксируем некоторый
уровень достоверности γ, 0<γ<1. Будем говорить, что число A
удовлетворяет ограничению B с уровнем достоверности γ ,
если выполнено соотношение
Это условие эквивалентно следующему неравенству:
Число NA(B)= называется степенью удовлетворения условию B.
18.
19.
20. 4. Оценка инновационных проектов на основе теории нечетких множеств
21.
Общепризнанными показателями, характеризующимиинвестиционный проект, служат такие величины, как
чистый дисконтированный доход NPV, внутренняя
норма возврата IRR, срок окупаемости и т.д. При
вычислении каждого из этих показателей денежный
поток проекта предполагается известным. Однако на
практике, как правило, невозможно получить точную
оценку потока проекта. В этом случае удобно
использовать нечёткие числа, параметры которых могут
быть оценены экспертами.
22.
Пусть денежный поток проекта задаётся как набортрапециевидных нечётких чисел Ct=(ct1,ct2,ct3,ct4),
t=0,1,2,3, ,T. Число ct1 интерпретируется как наименьшее
возможное значение потока в момент времени t, поток ни
при каких обстоятельствах не может опускаться ниже
этого значения, ct4 – наибольшее возможное значение, а
числа ct2 и ct3, образуют интервал, в пределах которого,
скорее всего, будет находиться значение денежного
потока. Довольно часто для оценки используют
треугольные нечёткие числа Ct=(ct1,ct2=ct3,ct4), при этом ct1
есть пессимистическая, ct4 – оптимистическая, а ct2 –
наиболее вероятная оценка денежного потока проекта.
Аналогичным образом, ставка дисконтирования также
представляется в виде нечёткого числа r=(r1,r2,r3,r4).
23.
Чтобы найти выражение для нечёткого NPV, нужно, как и в обычном случае,суммировать (нечёткие) дисконтированные значения для всех компонент
денежного потока:
T
NPV PV (Ct ).
t 0
В свою очередь, дисконтированное значение PV(Ct) получается применением
принципа расширения к классической формуле
Ct
PV (Ct )
.
t
(1 r )
В итоге получаем дисконтированный чистый денежный поток в момент t
max( ct1,0) min( ct1,0) max( ct 2 ,0) min( ct 2 ,0)
PV (Ct )
,
,
t
t
t
t
(1 r1 )
(1 r3 )
(1 r2 )
(1 r4 )
max( ct 3 ,0) min( ct 3 ,0) max( ct 4 ,0) min( ct 4 ,0)
.
,
t
t
t
t
(1 r2 )
(1 r3 )
(1 r1 )
(1 r4 )
24.
max( ct1,0) min( ct1,0) max( ct 2 ,0) min( ct 2 ,0)PV (Ct )
,
,
t
t
t
t
(1 r1 )
(1 r3 )
(1 r2 )
(1 r4 )
max( ct 3 ,0) min( ct 3 ,0) max( ct 4 ,0) min( ct 4 ,0)
.
,
t
t
t
t
(1 r2 )
(1 r3 )
(1 r1 )
(1 r4 )
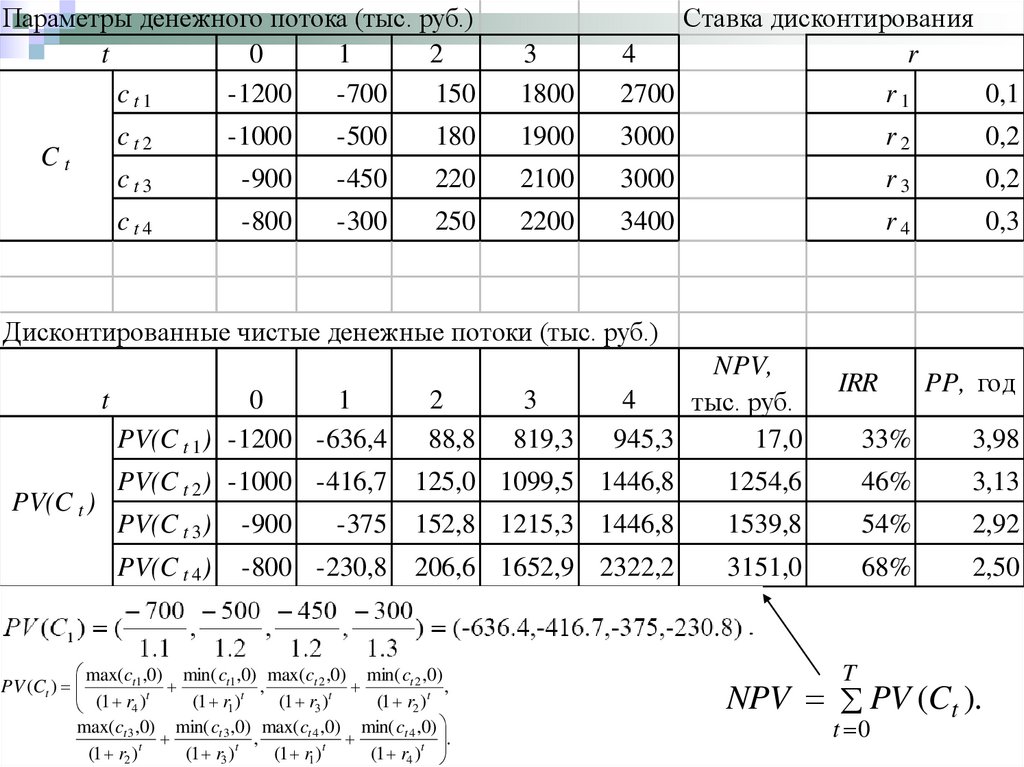
25.
Параметры денежного потока (тыс. руб.)t
0
1
2
c t1
-1200
-700
150
Ct
3
1800
Ставка дисконтирования
4
r
2700
r1
0,1
c t2
-1000
-500
180
1900
3000
r2
0,2
c t3
-900
-450
220
2100
3000
r3
0,2
c t4
-800
-300
250
2200
3400
r4
0,3
0,2
0,2
0,1
Дисконтированные чистые денежные потоки (тыс. руб.)
t
PV(C t )
0
1
PV(C t 1 ) -1200 -636,4
2
88,8
PV(C t 2 ) -1000 -416,7
125,0 1099,5 1446,8
-375 152,8 1215,3 1446,8
PV(C t 3 )
-900
PV(C t 4 )
-800 -230,8
3
819,3
NPV,
4
тыс. руб.
945,3
17,0
206,6 1652,9 2322,2
max( ct1,0) min( ct1,0) max( ct 2 ,0) min( ct 2 ,0)
PV (Ct )
,
,
t
t
t
t
(
1
r
)
(
1
r
)
(
1
r
)
(
1
r
)
4
1
3
2
max( ct 3 ,0) min( ct 3 ,0) max( ct 4 ,0) min( ct 4 ,0)
.
,
(1 r2 )t
(1 r3 )t
(1 r1 )t
(1 r4 )t
IRR
PP, год
33%
3,98
1254,6
46%
3,13
1539,8
54%
2,92
3151,0
68%
2,50
T
NPV PV (Ct ).
t 0
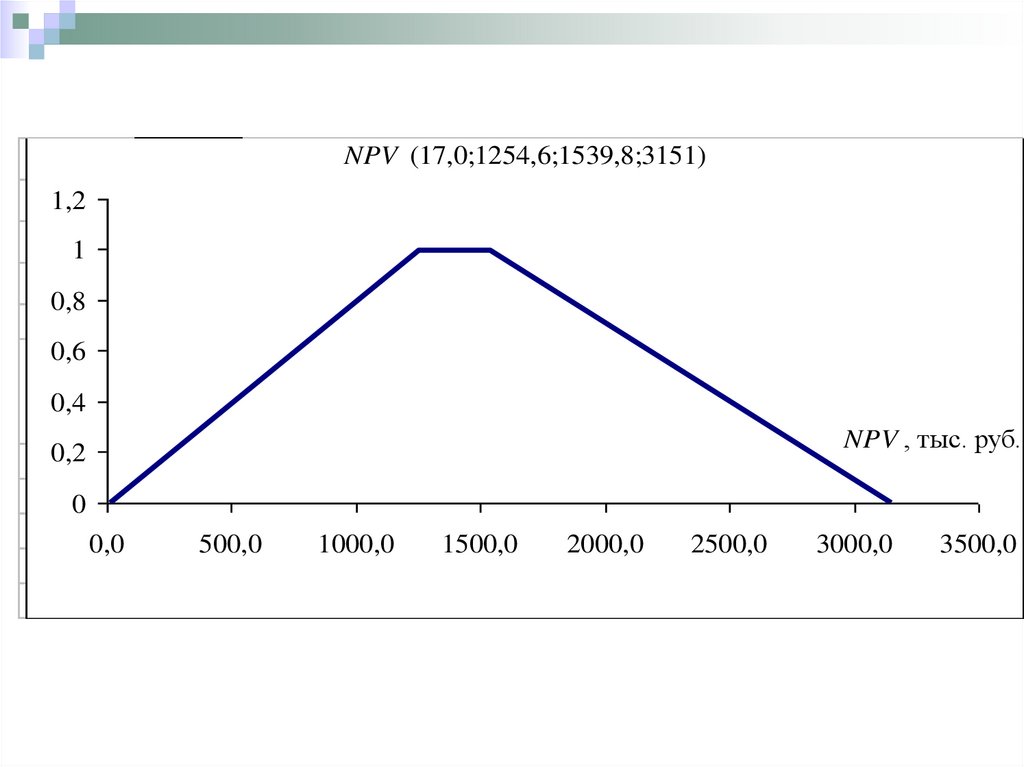
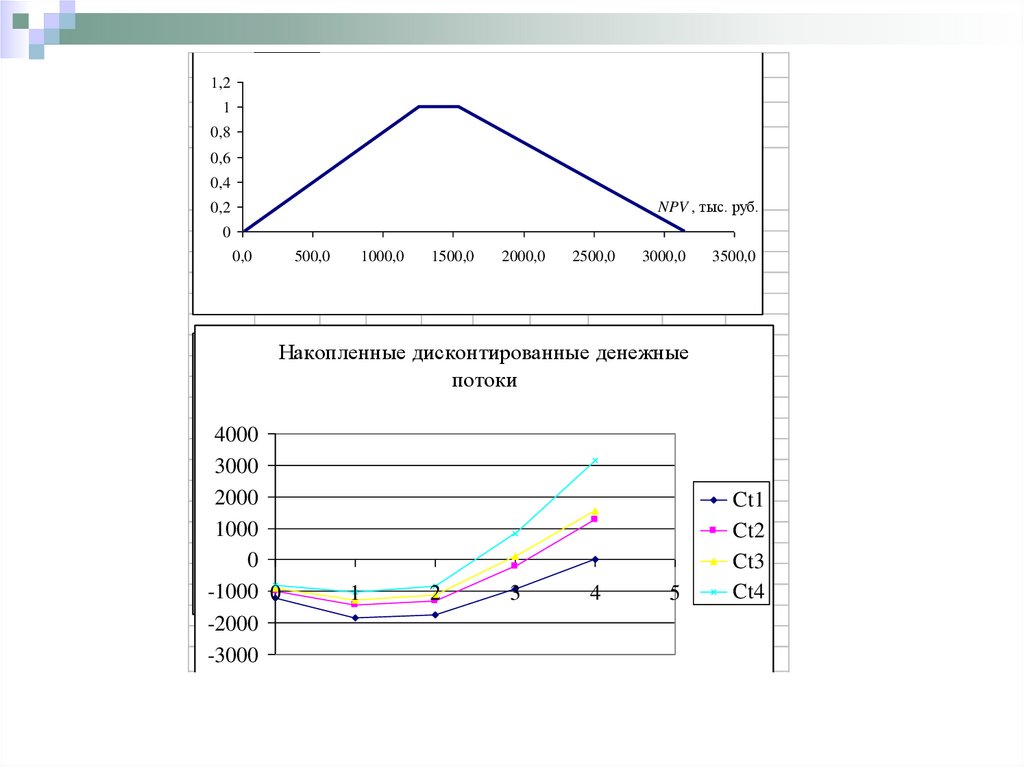
26.
-1836(17,0;1254,6;1539,8;3151)-1748 -928,3
17,0
S PV(C t 1 )-1200 NPV
1,2
1
0,8
0,6
0,4
0,2
0
0,0
S PV(C t 2 )-1000
S PV(C t 3 ) -900
-1417 -1292
S PV(C t 4 ) -800
-1031 -824,2 828,73 3151,0
NPV,
тыс.
руб.
17,0
1254,6
1539,8
500,0
3151,0
-192,1 1254,6
-1275 -1122 93,056 1539,8
0
1
11000,0
0
NPV , тыс. руб.
1500,0
2000,0
2500,0
3000,0
3500,0
27.
S PV(C t 2 ) -1000S PV(C t 3 ) -900
-1417 -1292
1,2
1
S PV(C t 4 ) -800
-1031 -824,2 828,73 3151,0
-192,1 1254,6
-1275 -1122 93,056 1539,8
0,8
0,6
NPV,
тыс. руб.
0,4
0,2
0
0,0
NPV , тыс. руб.
0
1
11000,0
0
17,0
1254,6
500,0
1539,8
3151,0
1500,0
2000,0
2500,0
3000,0
3500,0
0
2,50
денежные
(2,5;2,92;3,13;3,98)
дисконтированные
PP
Накопленные
1
2,92
потоки
1
3,13
1,2
1
4000
0,8
3000
0,6
0,4
2000
0,2
1000
0
2,000
-1000 0
-2000
-3000C t 1
0
3,98
2,50
1
0
-1200
2
4,00
3,50
3,00
3
4
3
2
1
-1836 -1748 -928,3 17,038
4
5
Ct1
год
Ct2
4,50
Ct3
Ct4
28. 5. Оценивание качественных показателей проекта при помощи нечётких множеств
29.
При оценке инвестиционного проекта, наряду с такими егочисловыми характеристиками проекта, как NPV,
используются качественные показатели. В качестве
примера таких показателей можно назвать
инновативность проекта,
соответствие проекта стратегическим целям компании,
экологичность проекта,
влияние на репутацию фирмы и т.д.
Качественные показатели обычно выражаются в виде
балльной оценки, проставляемой одним или несколькими
экспертами. В дальнейшем балльная шкала переводится в
числовую. Числа, полученные по разным показателям
одного проекта, агрегируются в один числовой показатель,
и данная общая оценка используется в процессе
ранжирования проектов.
30.
Появление нечётких множеств позволило сделатьпроцедуру перехода от балльной шкалы к числовой
более гибкой и адекватной мышлению человекаэксперта. Рассмотрим в качестве примера 5-балльную
шкалу качественных оценок проекта: «очень плохо»,
«плохо», «средне», «хорошо», «очень хорошо».
Каждому из баллов сопоставим трапециевидное
нечёткое число в соответствии с таблицей. Это число
будет считаться нечёткой оценкой показателя.
31.
Как видно, нечёткие числа зацеплены друг за друга. Это отражает тот факт, что нет резкогоразделения между соседними оценками, и переход от одной балльной оценки к другой
происходит постепенно. Результатом оценивания качественного показателя проекта
является нечёткое число, лежащее на отрезке от 0 до 1.
32.
В случае, когда при оценивании проекта рассматриваетсянесколько показателей, как качественных, так и
количественных, появляется необходимость в
сведении набора полученных оценок к одной общей
(интегральной) оценки. Процесс сведения
предполагает выполнение следующих действий:
1. Нахождение относительного веса для каждого
показателя;
2. Оценивание каждого показателя проекта нечётким
числом;
3. Нормировка количественных показателей;
4. Агрегирование нечётких оценок проекта с
заданными весами и получение общей оценки
проекта.
33.
34.
35.
36. 6. Ранжирование проектов в нечетком представлении
37. Ранжирование проектов в нечетком представлении
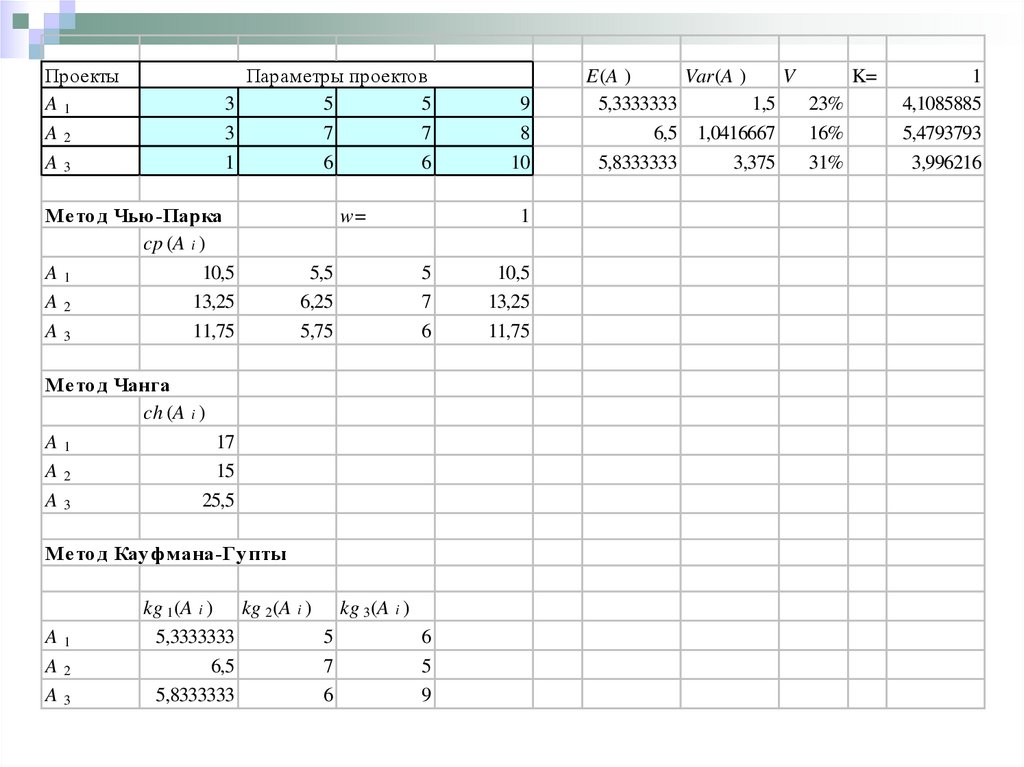
38.
39.
ПроектыA1
A2
A3
Параметры проектов
3
5
5
3
7
7
1
6
6
Мето д Чью-Парка
cp (A i )
A1
10,5
A2
13,25
A3
11,75
w=
5,5
6,25
5,75
1
5
7
6
Мето д Чанга
ch (A i )
A1
17
A2
15
A3
25,5
Мето д Кау фмана-Гу пты
A1
A2
A3
9
8
10
kg 1 (A i ) kg 2 (A i ) kg 3 (A i )
5,3333333
5
6
6,5
7
5
5,8333333
6
9
10,5
13,25
11,75
E(A )
Var(A )
V
K=
5,3333333
1,5
23%
6,5 1,0416667
16%
5,8333333
3,375
31%
1
4,1085885
5,4793793
3,996216
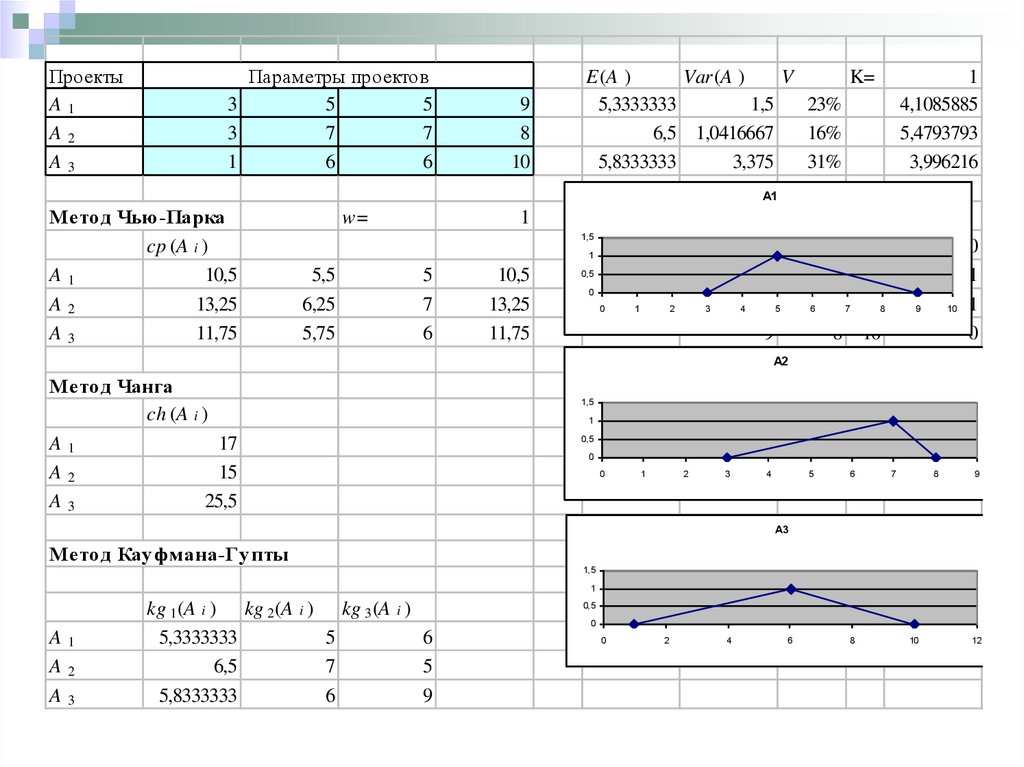
40.
ПроектыA1
A2
A3
Параметры проектов
3
5
5
3
7
7
1
6
6
9
8
10
E(A )
Var(A )
V
K=
5,3333333
1,5
23%
6,5 1,0416667
16%
5,8333333
3,375
31%
1
4,1085885
5,4793793
3,996216
А1
Мето д Чью-Парка
cp (A i )
A1
10,5
A2
13,25
A3
11,75
w=
1
A1
A2
1,5
1
5,5
6,25
5,75
5
7
6
10,5
13,25
11,75
0,5
0
0
1
2
3
4
3
5
55
9
6
A3
3 1
7 6
7 7 68
8 10
0
1
10 1
0
9
А2
Мето д Чанга
ch (A i )
A1
17
A2
15
A3
25,5
1,5
1
0,5
0
0
1
2
3
4
5
6
7
8
9
А3
Мето д Кау фмана-Гу пты
1,5
1
A1
A2
A3
kg 1 (A i ) kg 2 (A i ) kg 3 (A i )
5,3333333
5
6
6,5
7
5
5,8333333
6
9
0,5
0
0
2
4
6
8
10
12



































 mathematics
mathematics








