Similar presentations:
Помехоустойчивое кодирование. Коды Рида-Маллера
1. Помехоустойчивое кодирование
Коды Рида-Маллера2. Отождествление булевых функций с их таблицами (столбцами)
x1 x2f ( x1 , x2 )
0
0
0
0
1
1
1
0
0
1
1
1
0
1
f ( x1 , x2 )
0
1
3. Покомпонентное произведение кодовых слов
(a0 , a1 ,..., an 1 )T
и
(b0 , b1 ,..., bn 1 )
(a0b0 , a1b1 ,..., an 1bn 1 )
T
T
4. Степень булевой функции
степень коньюнкцииdeg xi1 xi2 ... xik k
степень функции
deg f ( x1 , x2 ,... xn )
наибольшая из степеней конъюнкций ,
входящих в полином Жегалкина
(полином Рида Маллера )
5. Пример
степень коньюнкцииdeg x1 x3 x4 3
степень функции
f ( x1 , x2 ,... xn ) x1 x1 x2 x2 x3
равна 2
6. Определение
• Код Рида-Маллера порядка r (РМ-r – код)– это множество булевых функций
степени не выше r.
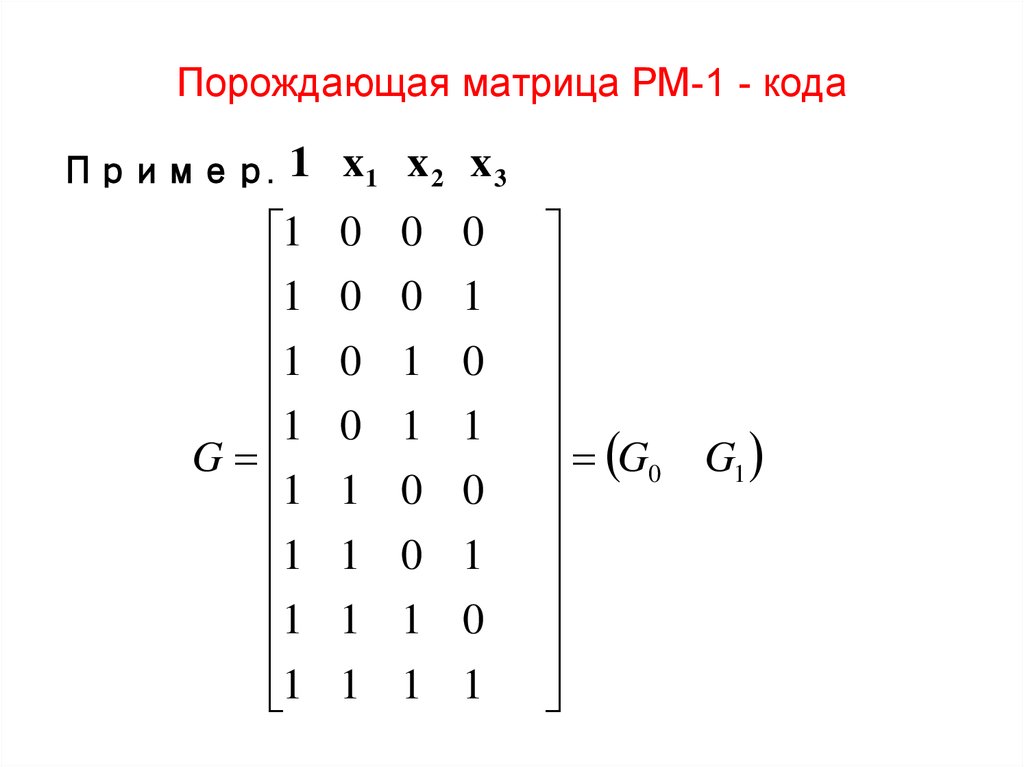
7. Порождающая матрица РМ-1 - кода
Пример.1 x1 x 2 x 3
1
1
1
1
G
1
1
1
1
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
G
0
G1
8. Порождающая матрица РМ-2 - кода
Пример.1 x1 x 2 x 3 x1 x 2 x1 x 3 x 2 x 3
1
1
1
1
G
1
1
1
1
0 0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
1
1
0
0
1
0
0
0
0
1
0
1
0
1
1
1
0
1
0
1
1
1
1
1
0
0
0
1
G0
0
0
0
1
G1 G2
9. Параметры РМ-r - кода
Длина кодаn 2
m
Число информационных разрядов
k 1 m C ... C
2
m
Минимальное расстояние
r
m
d min 2
m r
10. Пример параметров РМ-2 - кода
Длина кодаn 2 16,
4
m 4
Число информационных разрядов
k 1 4 C 1 4 6 11
2
4
Минимальное расстояние
d min 2
m r
4
11. Пример параметров РМ-3 - кода
Длина кодаn 2 16,
4
m 4
Число информационных разрядов
k 1 4 C C 1 4 6 4 15
2
4
3
4
Минимальное расстояние
d min 2
4 3
2
12. Кодированиe – блоки информационного и кодового слова
01
G G0 G1 ... Gr
...
r
G0 0 G1 1 ... Gr r
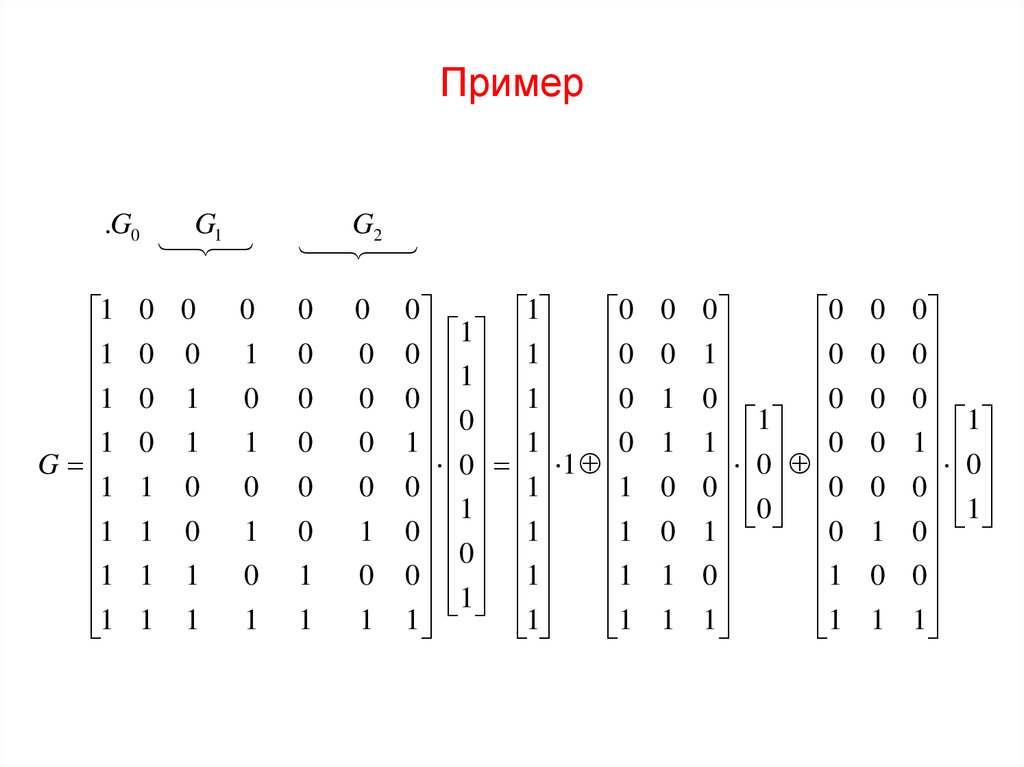
13. Пример
.G01
1
1
1
G
1
1
1
1
G
1
G2
0 0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
1
1
0
0
1
0
0
0
0
1
0
1
0
1
1
1
0
1
0
1
1
1
1
1
0
1
0
1
0
0 1
1
0
0 1
0
1 1
0
0
1
1
0
1
1
0 1
1
0
1
0 1
1
1
1
1
0 0
0
0
0 1
0
1 0
1
1 1 0
0
0
0 0
0
0 1
0
1
1 0
1 1
1
0 0
0 0
0 0
1
0 1
0
0 0
1
1 0
0 0
1 1
14. Построение проверок - на примере РМ-1 кода длины 16
11
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0 0 0 0
c0 a0
0 0 0 1
c1 a0 a4
c0 c1 c2 c3 0
0 0 1 0
c2 a0 a3
0 0 1 1
c3 a0 a3 a4
0 1 0 0
c 4 a0 a 2
c4 c5 c6 c7 0
0 1 0 1
c5 a0 a2 a4
a
c0 c1 c4 c5 0
0
0 1 1 0
c6 a0 a2 a3
c c c c 0
a1
0
2
4
6
0 1 1 1
c7 a0 a2 a3 a4
a2
1 0 0 0
c8 a0 a1
a3
1 0 0 1
c9 a0 a1 a4
a4
c8 c9 c10 c11 0
1 0 1 0
c10 a0 a1 a3
c11 a0 a1 a3 a4
1 0 1 1
1 1 0 0
c12 a0 a2
c12 c13 c14 c15 0
1 1 0 1
c13 a0 a2 a4
c8 c9 c12 c13 0
c14 a0 a2 a3
1 1 1 0
c8 c10 c12 c14 0
c15 a0 a1 a 2 a3 a4
1 1 1 1
15. Построение проверок - на примере РМ-1 кода длины 16 – шаг 1
a4 c0 c1 c2 c3 c4 c5 c6 c7c8 c9 c10 c11 c12 c13 c14 c15
a3 c0 c2 c1 c3 c4 c6 c5 c7
c8 c10 c9 c11 c12 c14 c13 c15
a2 c0 c4 c1 c5 c2 c6 c3 c7
c8 c12 c9 c13 c10 c14 c11 c15
a1 c0 c8 c1 c9 c2 c10 c3 c11
c4 c12 c5 c13 c6 c14 c7 c15
16. Построение проверок - на примере РМ-1 кода длины 16 – шаг 2
a0 c0 c1 c2 c3 c4 c5 c6 c7c8 c9 c10 c11 c12 c13 c14 c15
17. Мажоритарное декодирование РМ - кодов
• Строятся проверки дляr
всего 2m r проверок
• Затем – для
и т.д.
r 1 всего 2
m r 1
• На последнем шаге исправляется
0 a0 всего 2 проверок
m
проверок
18. Циклический код Рида-Маллера
• Рассмотрим разложение числа j постепеням двойки:
j j0 j1 2 j2 4 ... jm 1 2 m 1
• Весом целого числа j в двоичном
разложении назовем сумму
w2 ( j ) j0 j1 ... jm 1
• Пример. 7=1+2+4, m=3, (111), w2 (7) 3
• 12=4+8, m=4 (0011), w2 (12) 2
19. Циклический код Рида-Маллера
• Циклическим кодом Рида Маллера порядкаm
r и длины n 2 1
над полем GF(2)
назывется циклический код, порождающий
j
многочлен g(x) которого имеет корни
такие, что
0 w2 ( j ) m r 1,
j 1,..., n
20. Циклический код Рида-Маллера
• Заметим, что если является корнемg(x), то и 2 j является корнем.
j
21. Параметры циклического РМ-кода
Параметры циклического РМкода• Длина:
n 2 1
m
• Число информационных разрядов:
r
k C
i 0
i
m
• Минимальное расстояние:
d min 2
m r
1
22. Циклический РМ – код порядка m-2
0 w2 ( j ) m (m 2) 1,j 1,..., n w2 ( j ) 1
корнями
являются
, 2 , 4 ,...
• Это циклический код Хэмминга
23. m=5, циклический РМ – код порядка r=2
0 w2 ( j ) 5 2 1 2,j 1,..., n w2 ( j ) 1,2
корнями
являются , , :
3
5
00001, 00011, 00101
и их циклически е сдвига
• Это (31,16) – код БЧХ, исправляющий 3
ошибки
24. Связь между обычными и циклическими РМ - кодами
• Обычный РМ код получается из циклическогодобавлением одного проверочного разряда –
разряда проверки на четность.
25. Преимущества циклического РМ кода
• Декодирование – мажоритарное, циклическийсдвиг кодового слова соответствует
циклическому сдвигу проверок.
26. Код, дуальный к циклическому РМ- коду порядка r=m-2
• Длина: n 2 m 1• Число информационных разрядов:
k 2m 1 (1 m ...Cmm 2 )
2m 1 (2m Cmm 1 Cmm ) m
• Минимальное расстояние:
d min 2
m 1
27. Код, дуальный к циклическому РМ- коду порядка r=m-2
• Пример. m=4, n=15.• Порождающий многочлен
1 x15
g ( x)
4
1 x x
1 x x x x x x x
2
3
5
7
• Некоторые кодовые слова:
111101011001000
011110101100100
100011110101100
101100100011110
8
11
28. Код, дуальный к циклическому РМ- коду порядка r=m-2
• Рассмотрим подробнее слово:111101011001000 | 11…
Число нулей и единиц – ½ длины слова
Число биграмм 00,01,10,11 – ¼ длины слова
Число триграмм – 1/8 длины слова
Автокорреляция
111101011001000
011110101100100
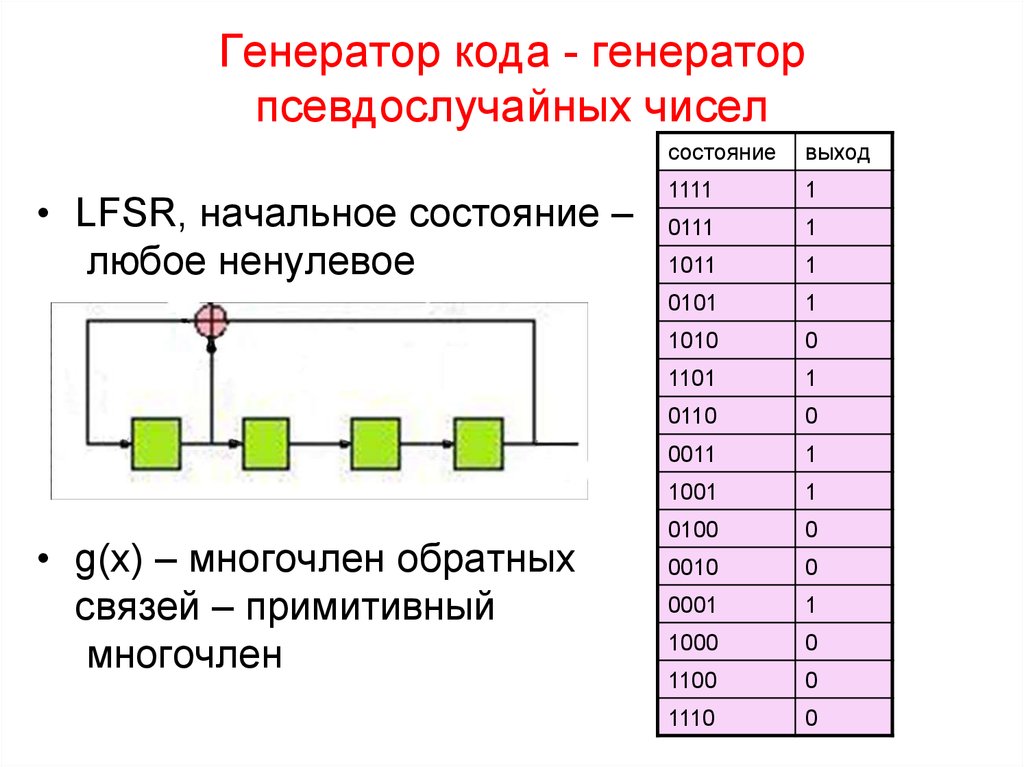
29. Генератор кода - генератор псевдослучайных чисел
• LFSR, начальное состояние –любое ненулевое
• g(x) – многочлен обратных
связей – примитивный
многочлен
состояние
выход
1111
1
0111
1
1011
1
0101
1
1010
0
1101
1
0110
0
0011
1
1001
1
0100
0
0010
0
0001
1
1000
0
1100
0
1110
0
30. Периодические последовательности на LFSR
• Примитивный многочлен степени m – последовательностимаксимальной длины (период равен
2m 1 - порядок
многочлена)
• В других случаях период последовательности – порядок
многочлена ОС
многочлен
период
• Примеры.
1 x4
4
1 x x4
1 x2 x4
1 x3 x 4
1 x x2 x4
1 x x3 x 4
1 x 2 x3 x 4
1 x x 2 x3 x 4
15
6
15
7
6
7
5
31. Некоторые часто используемые примитивные трехчлены
x x 1, x x 1, x x 1,3
4
5
2
x 31 x 3 1, x 31 x 6 1, x 31 x 7 1,
x x 1, x x 1, x x 1,
39
4
60
63
x 71 x 6 1, x 93 x 2 1, x137 x 21 1,
145
x
x 1, x
52
161
x 1, x
18
521
x 1
32




























 informatics
informatics








