Similar presentations:
Циклические коды
1. Циклические коды
2. Циклические коды (ЦК)
Подкласс линейных кодов
Кодирование и декодирование основано на:
1. Полиномиальном представлении
2. Операторах сдвига (регистрах сдвига с обратной
связью РСОС)
• Это упрощает решение задач ТК
3. Определение.
• Линейный (n, k)-код C над полем Fqназывается циклическим, если из того,
что вектор
• с = (c0, c1, …, cn-1)
• принадлежит C, следует, что его
циклический сдвиг
• с(1) = (cn-1, c0, c1, …, cn-2 )
• принадлежит C.
4. Циклический блоковый код
с = (с 0 , с1 , с 2 ,..., с n-1 )с
(i )
“i” циклический сдвиг с
= (с n-i , с n-i +1 ,..., с n -1 , с 0 , с1 , с 2 ,..., с n-i -1 )
Пример
с = (1101)
с
(1)
= (1110 ) с
( 2)
= (0111) с
( 3)
= (1011) с
( 4)
= (1101) = с
5. ЦК - полиномы Алгебраическая структура
• Кодовые слова представляются как многочлены от xстепени не выше n – 1
• c = (c0, c1, …, cn – 1) c(x) = c0 + c1 x + …+ cn-1 xn – 1.
• Соотношения между кодовым словом и циклическими
сдвигами:
x c ( x ) = c 0 x + c1 x 2 + ..., c n-2 x
В полиномиальном
представлении
циклический сдвиг
на одну позицию
соответствует
умножению на
(xn – 1):
+ c n-1 x
n
= c n-1 + c 0 x + c1 x 2 + ... + c n-2 x n-1 + c n-1 x n - c n-1
144444
4(2
444444
3 142
4 n43
4
1)
c
=c
(1)
(x )
un -1 ( x -1)
( x ) + c n-1 ( x n - 1)
По индукции
c
x
по модулю
n -1
c
(i )
(1)
(x ) = x c (x )
( x ) = x ic ( x )
mod ( x n - 1)
mod ( x n - 1)
6. Генераторный полином
Важным свойством циклических кодов является то, что всекодовые слова-полиномы кратны одному фиксированному
полиному g(x), который называется порождающим
полиномом кода. Порождающий полином g(x) является
делителем бинома ( x n – 1).
c( x) = a( x)g( x) mod(x n - 1)
g( x) = g0 + g1x + ... + g r x r
Множество {xi g(x); 0 i k – 1}можно рассматривать как
базис размерности k циклического кода С.
7. Генераторная матрица
• Генераторная матрица кода представляетсяматрица размером (k n) следующего вида
g ( x) g 0
x g ( x) 0
2
G = x g ( x) = 0
x k -1 g ( x) 0
g1
...
gn-k
0
...
g0
...
...
gn-k
...
0
g0
g1
...
gn-k
0
0
...
g0
...
как
0
0
...
g n - k
• Строки матрицы G линейно независимы, и таким
образом, ранг матрицы G равен k – размерности кода
C. С помощью такой матрицы осуществляется
несистематическое кодирование.
8. Пример
• Циклический код Хэмминга• (7, 4, 3)
• задается порождающим полиномом
• g(x) = x3 + x + 1,
• имеющий двоичное представление в
виде кода
• g = (1101).
• Требуется. Построить порождающую
матрицу систематического кода.
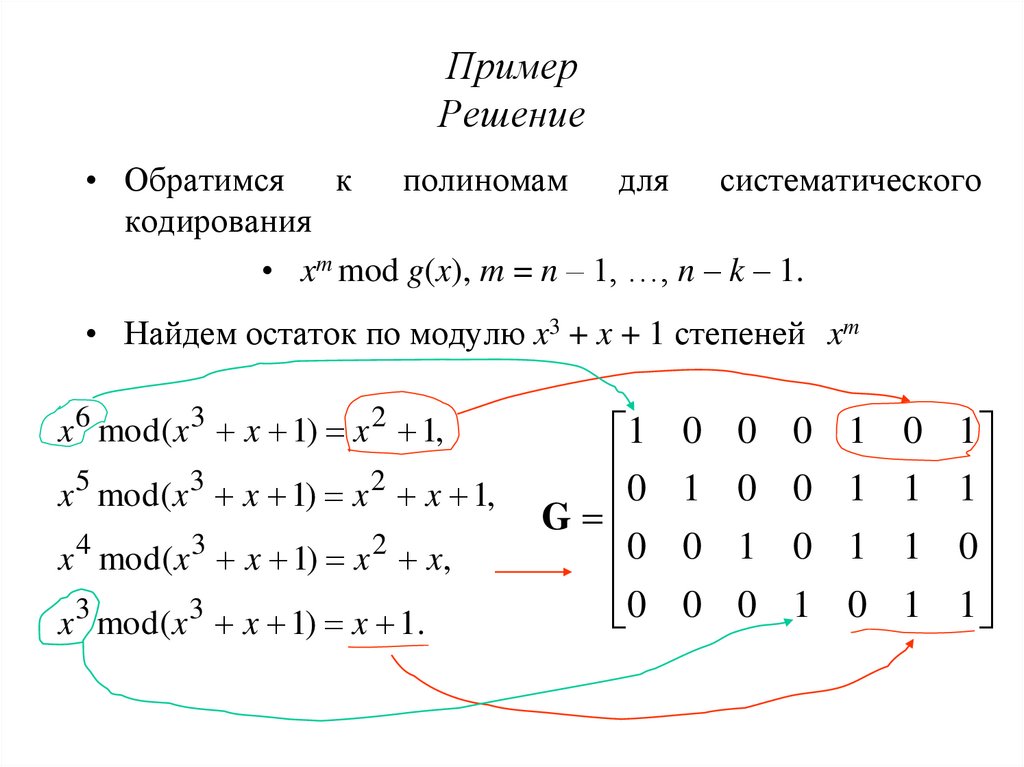
9. Пример Решение
• Обратимся к полиномам для систематическогокодирования
• xm mod g(x), m = n – 1, …, n – k – 1.
• Найдем остаток по модулю x3 + x + 1 степеней xm
x 6 mod(x 3 + x + 1) = x 2 + 1,
x 5 mod(x 3 + x + 1) = x 2 + x + 1,
x 4 mod(x 3 + x + 1) = x 2 + x,
x 3 mod(x 3 + x + 1) = x + 1.
1
0
G=
0
0
0 0 0 1 0 1
1 0 0 1 1 1
0 1 0 1 1 0
0 0 1 0 1 1
10. Требования к порождающему полиному :
• 1.g(x) должен быть ненулевым;
• 2.
вес g(x) не должен быть меньше минимального
кодового расстояния:
;
wt ( g ( x)) d min
• 3.
g(x) должен иметь максимальную степень (n – k),
которая определяет число избыточных элементов в
коде;
• 4.
g(x) должен быть делителем полинома (x n – 1).
11. Факторизация бинома ( x n – 1)
• Разложим бином ( x n – 1) на множители mj(x), j = 1, 2,…, l,
• ( x n – 1) = m1(x) m2(x) … ml(x).
• Представим многочлен ( x n – 1) как произведение
минимальных многочленов
x n - 1 = mi ( x)
i J
где J – множество индексов.
12. Проверочный многочлен h(x)
• Разобьем факторизованное множество на дванепересекающихся подмножеств – Jg и Jh – так, что
• J = Jg Jh .
• Введем два полинома
g ( x) = mi ( x) = g 0 + g1x + g 2 x 2 + ... + g r x r
i J g
h( x) = mi ( x) = h0 + h1x + h2 x 2 + ... + hk x k
i J h
Многочлены g(x) и h(x) удовлетворяют условию
g(x) h(x) = (x n – 1).
13. Проверочный многочлен h(x)
• Если полином g(x) - порождающий, то любое кодовоеслово можно представить в виде
• c(x) = a(x) g(x),
• где a(x) – информационный полином. Следовательно,
имеет место равенство
• c(x) h(x) = a(x) g(x) h(x) = a(x)(xn – 1).
• Откуда следует, что
• c(x) h(x) 0 mod (xn – 1).
• Многочлен h(x) называется проверочным полиномом,
он может быть вычислен как
xn - 1
h( x ) =
g ( x)
14. Проверочная матрица
• Проверочная матрица циклического кода C имеет вид0
0
H=
hk
0
0
0 hk
0
hk -1
hk
h0
hk -1
hk -1
h0
0
h0
0
0
• или
hk
0
H=
0
hk -1
hk
h0
h2
h1
0
0
hk
0
h0 0 0 0
hk -1
h1 h0
0
0
0
15. Соотношение степеней
• Для циклического кода число информационныхсимволов k и число проверочных символов r
определяется как
k = deg h( x)
r = deg g ( x)
• Код с порождающей матрицей H , т. е. код, дуальный к
коду C , также является циклическим кодом.
• Кодовые слова по полиному h(x) образуют нуль
пространство относительно кодовых слов построенных
по полиному g(x).
16. Пример
• Построить циклический код над GF(2) длины n = 31 счислом проверочных символов r = 16.
• Решение. Проведем факторизацию (разложение на
множители) полинома x31 – 1
x 31 - 1 = m0 ( x)m1 ( x)m3 ( x)m5 ( x)m7 ( x)m11 ( x)m15 ( x) mod 2
• Множество индексов J имеет вид J = {0, 1, 3, 5, 7, 11, 15}.
• Для r = 16 выберем полином
g ( x) = m0 ( x)m1 ( x)m3 ( x)m5 ( x) = x16 + x15 + x12 + x 7 + x 6 + x 5 + x 4 + 1
Для k = 15, проверочный полином
h( x) = m7 ( x)m11( x)m15 ( x) = x15 + x14 + x13 + x12 + x10 + x8 + x 7 + x 6 + x5 + x 4 + 1
17.
18. Пример
19. Пример
20. Пример
21.
22.
23.
24. Проверочная матрица
25.
26.
27.
28. Сравнительный анализ
29.
30. Вычисление синдрома
31. Вычисление синдрома
32. Кодирование циклических кодов Кодирование с помощью порождающего полинома g(x).
• Несистематическое кодированиеc( x) = a ( x) g ( x)
• Систематическое кодирование
c( x) = x
n-k
a( x) + rem{x
n-k
a( x) / g ( x)}
• где a(x) – полином информационного сообщения.
33. Систематическое кодирование
• Полином кодового слова c(x) находится с помощьюсоотношения
• c(x) = a(x) + b(x),
• где
a( x) = a0 x n -1 +a1x n - 2 + ... + ak -1x n - k
• многочлен информационных символов;
b( x) = ck x r -1 + ck +1x r - 2 + ... + cn - 2 x + cn -1
• многочлен проверочных символов.
• Для нахождения многочлена проверочных символов при
систематическом кодировании достаточно разделить многочлен
информационных символов на порождающий полином.
• Остаток от деления и будет искомым многочленом проверочных
символов
34. Пример
Для систематического циклического
кода Хэмминга (7, 4) генераторный
полином равен
g ( x ) = 1 + x + x3
1. Найти кодовое слово для сообщения
a = (1011)
35. Решение
n = 7, k = 4, n - k = 3a = (1011) a( x) = 1 + x 2 + x3
x n - k a ( x) = x3a ( x) = x3 (1 + x 2 + x3 ) = x3 + x5 + x 6
Разделим x n - k a ( x) на g ( x) :
x3 + x5 + x 6 = (1 + x + x 2 + x3 )(1 + x + x3 ) +
1
1442443 14243
1
424
3
целая часть q(x)
g(x)
остаток b( x )
Полином кодового слова :
c( x) = b( x) + x3a ( x) = 1 + x3 + x5 + x 6
c=(
112
030
1102131
проверочные символы информационная часть
)
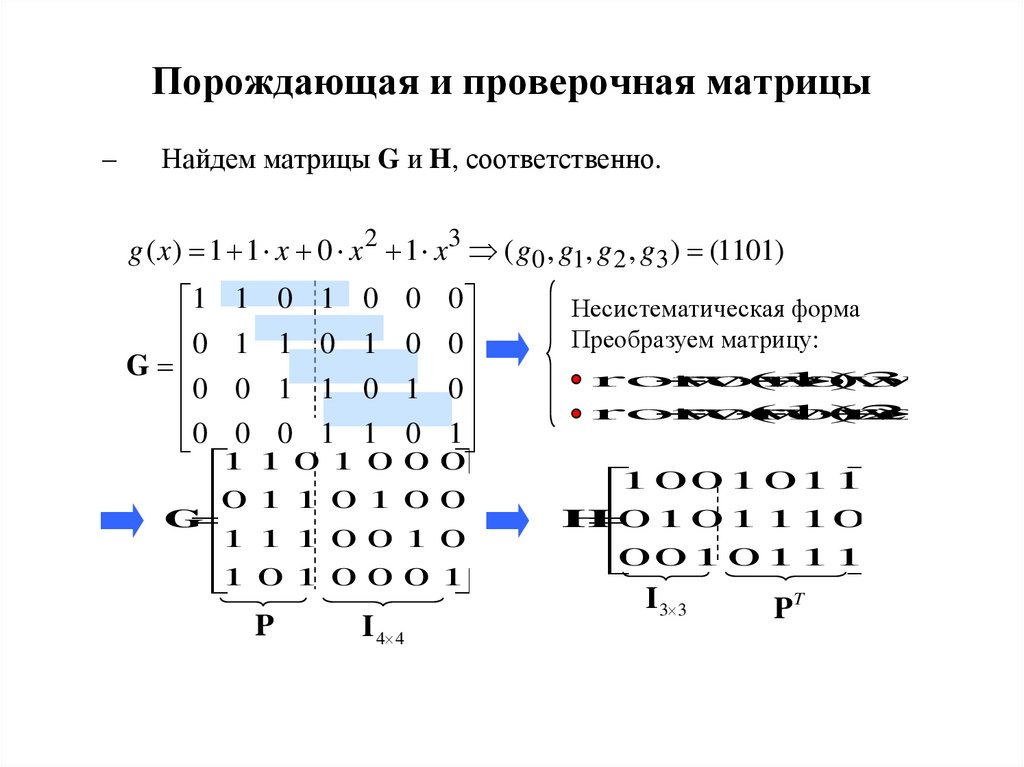
36. Порождающая и проверочная матрицы
–Найдем матрицы G и H, соответственно.
g ( x) = 1 + 1 x + 0 x 2 + 1 x3 ( g0 , g1, g 2 , g3 ) = (1101)
1
0
G=
0
0
1 0 1 0 0 0
1 1 0 1 0 0
0 1 1 0 1 0
0 0 1 1 0 1
1
0
G
=
1
1
1 0 1 0 0 0
1 1 0 1 0 0
1 1 0 0 1 0
0 1 0 0 0 1
P
I 4 4
Несистематическая форма
Преобразуем матрицу:
row(1)
+
row(3)
row(3)
row(1)
+
row(2)
+
row(4)
row(
1 0 0 1 011
H
=
0
1
0
1
1
1
0
0 0 1 0 111
I 3 3
PT
37. Кодирование циклическим кодом с помощью проверочного многочлена h(x)
• Систематическоекодирование
низкоскоростным
циклическим кодом удобно проводить с помощью
проверочного полинома, имеющего в данном случае
меньшую размерность, чем порождающий многочлен.
• Коэффициенты многочлена проверочных символов
b(x) вычисляются по коэффициентам многочленов c(x)
и h(x) следующим образом
k -1
bi = ck +i = h j ci + j , i = 0,1,...,n - k - 1
j =0
• что вытекает из равенства cHT = 0. Эти соотношения
позволяют по заданным информационным символам
вычислить проверочный символ ck, затем, зная ck,
вычислить ck + 1 и т. д.
38. Умножение и деление полиномов
• Умножение• a(x) = ak xk +ak-1 xk-1+ …+ a1 x +a0
• h(x) = hr xr +hr xr-1 + … + h1 x +h0
• a(x)h(x) =ak hr xk+r+ (ak-1 hr +ak hr-1) xk+r-1 +
• (ak-2 hr + ak-1 hr-1 + ak hr-2) xk+r-2 + …
• …+ (a0 h2 + a1 h1 + a2 h2)x2 + (a0 h1 + a1 h0 ) x + a0 h0
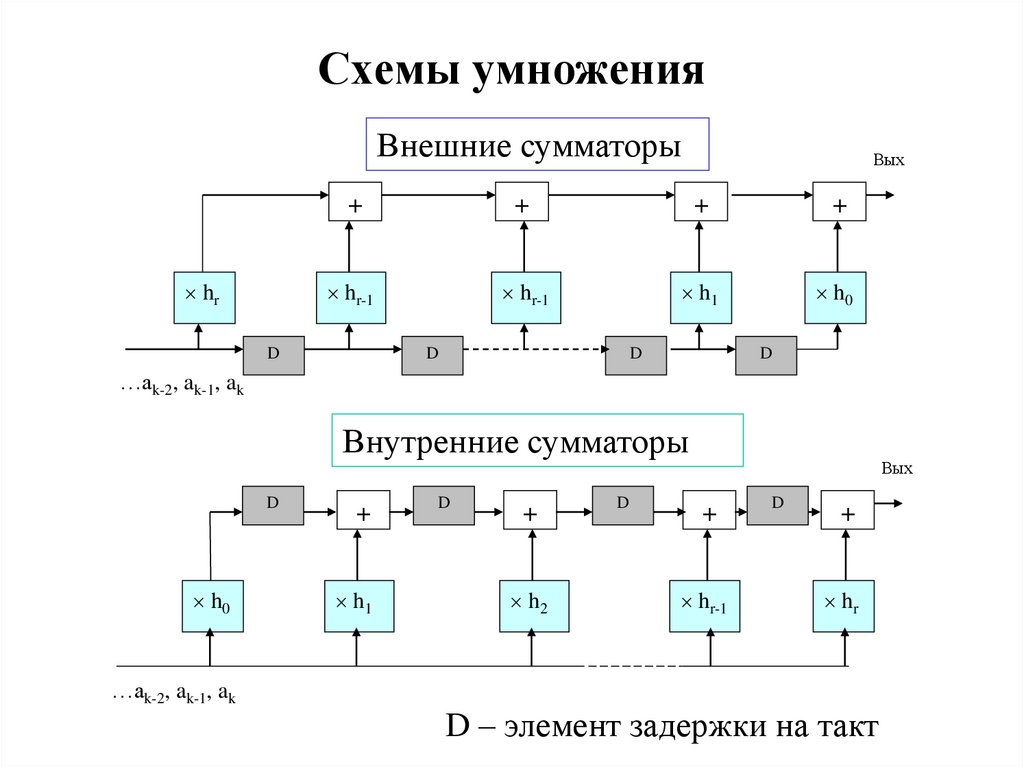
39. Схемы умножения
Внешние сумматорыhr
Вых
+
+
+
+
hr-1
hr-1
h1
h0
D
D
D
D
…ak-2, ak-1, ak
Внутренние сумматоры
D
h0
…ak-2, ak-1, ak
+
h1
D
+
h2
D
Вых
+
hr-1
D
+
hr
D – элемент задержки на такт
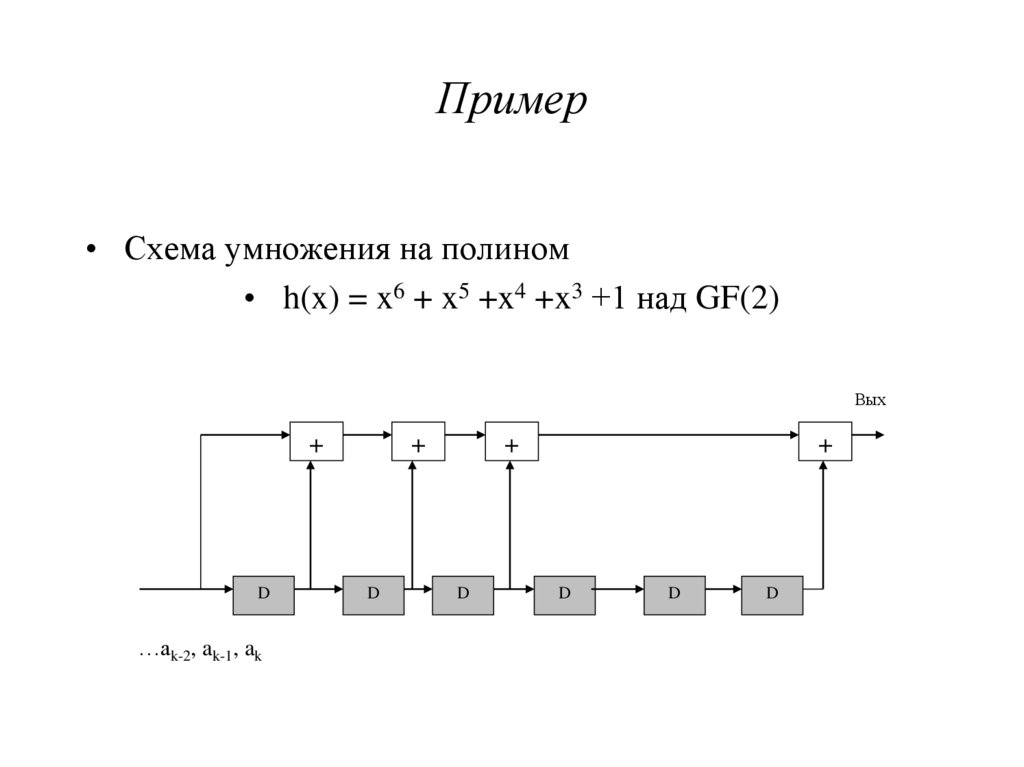
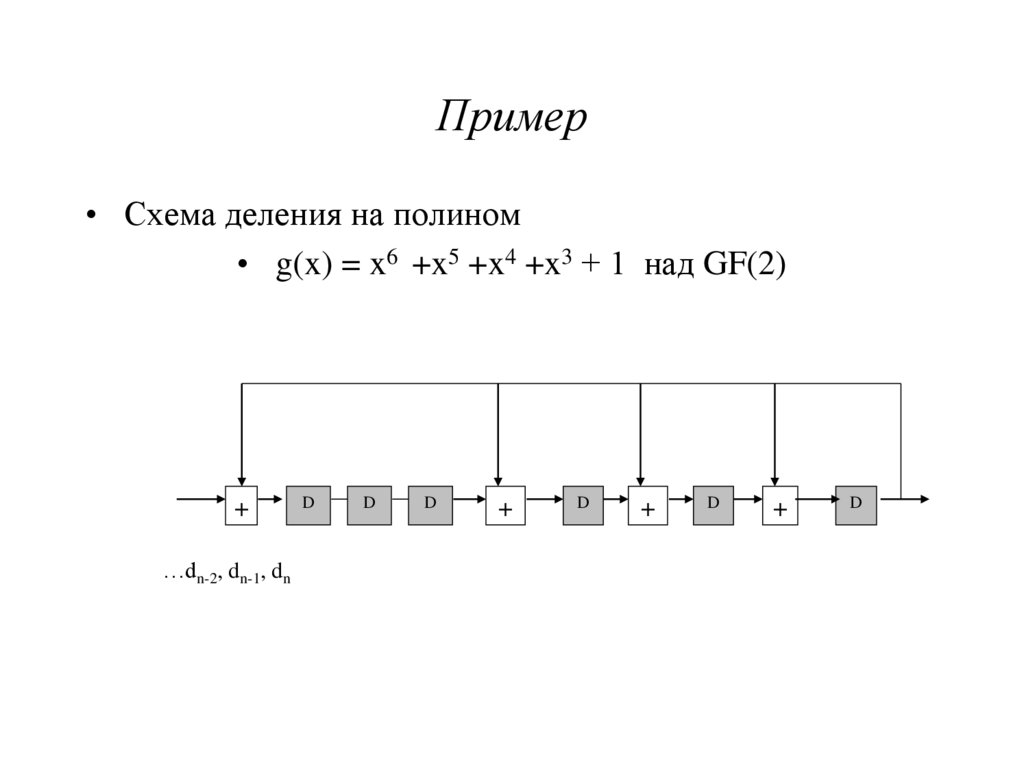
40. Пример
• Схема умножения на полином• h(x) = x6 + x5 +x4 +x3 +1 над GF(2)
Вых
+
D
…ak-2, ak-1, ak
+
D
+
D
+
D
D
D
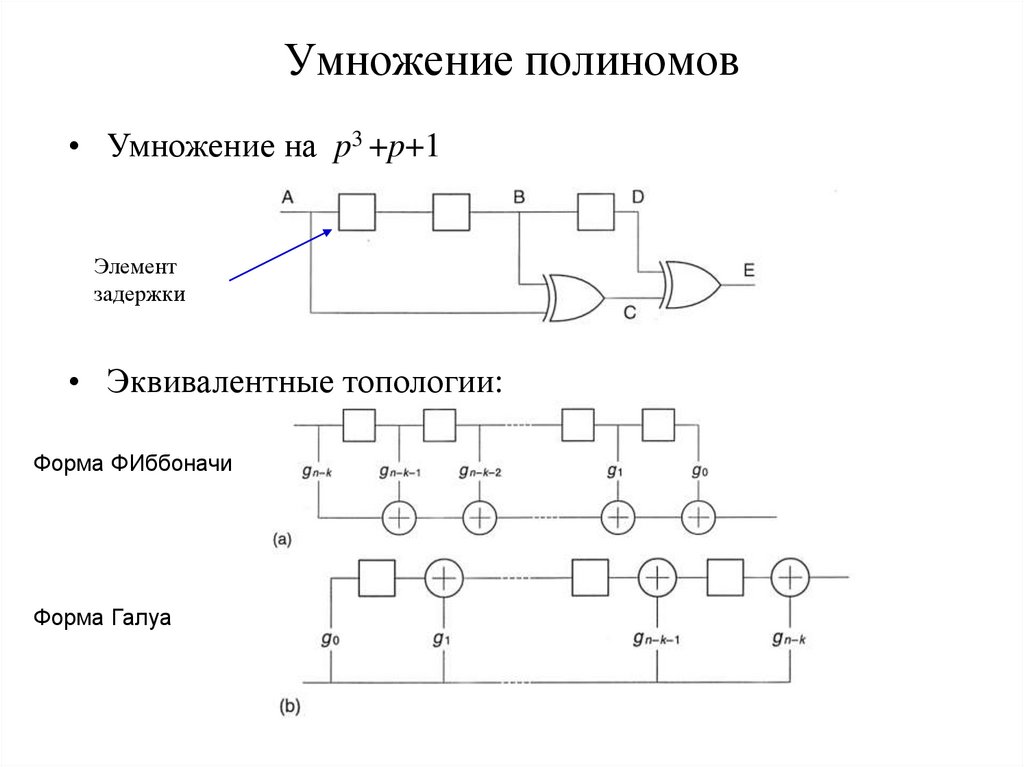
41. Умножение полиномов
• Умножение на p3 +p+1Data in
Элемент
unit delay
задержки
xn-1
x1
x0
Encoded bits
element
• Эквивалентные топологии:
Note that the tap order
is opposite in these
topologies
Форма ФИббоначи
Форма Галуа
XOR-circuit
Delay
element
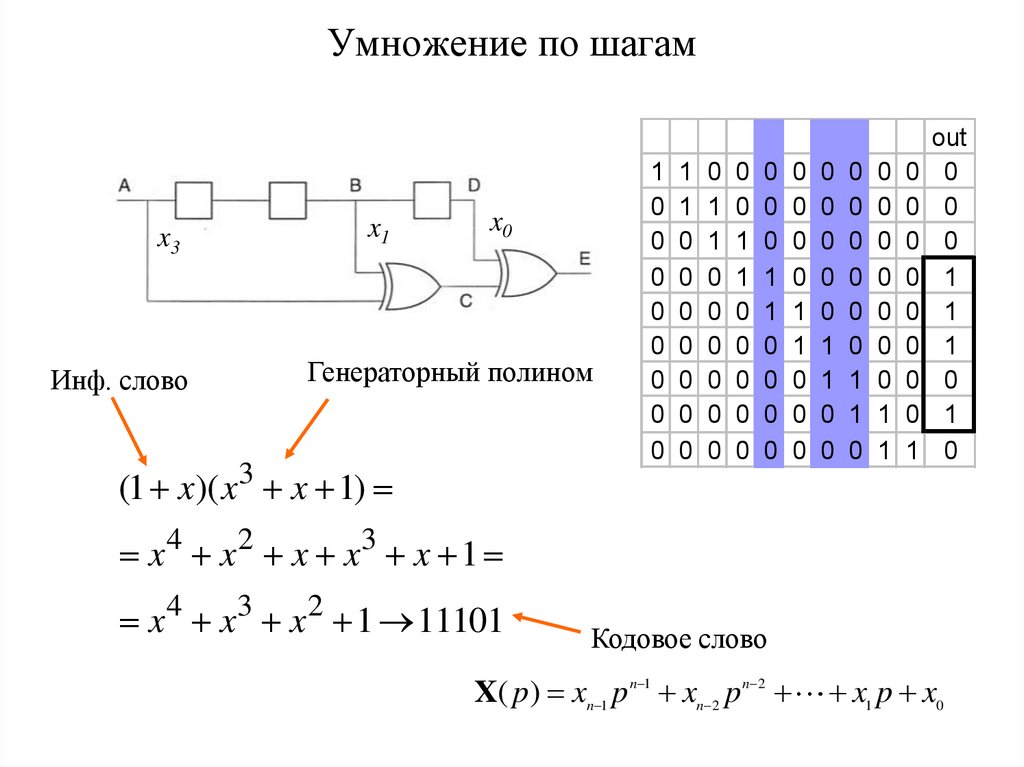
42. Умножение по шагам
x3Инф. слово
x1
x0
Генераторный полином
(1 + x)( x3 + x + 1) =
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
out
0
0
0
1
1
1
0
1
0
= x 4 + x 2 + x + x3 + x + 1 =
= x 4 + x3 + x 2 + 1 11101
Кодовое слово
X( p) = xn-1 p n-1 + xn-2 p n-2 +
+ x1 p + x0
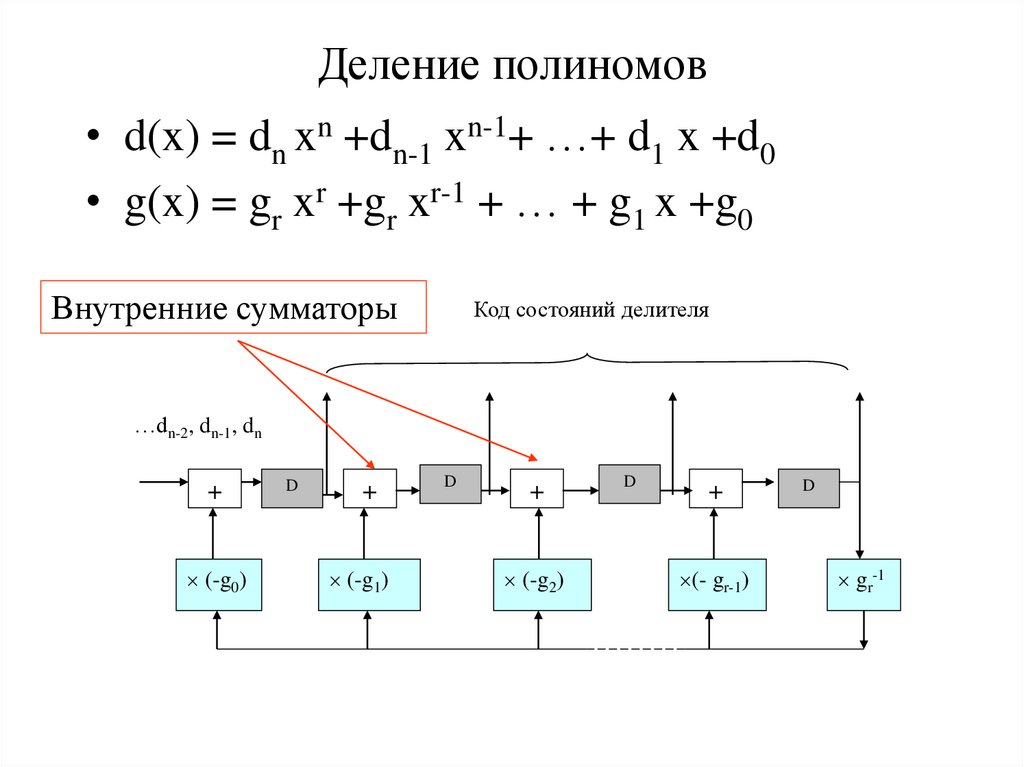
43. Деление полиномов
• d(x) = dn xn +dn-1 xn-1+ …+ d1 x +d0• g(x) = gr xr +gr xr-1 + … + g1 x +g0
Внутренние сумматоры
Код состояний делителя
…dn-2, dn-1, dn
+
(-g0)
D
+
(-g1)
D
+
(-g2)
D
+
(- gr-1)
D
gr-1
44. Деление полиномов
Внешние сумматоры…dn-2, dn-1, dn
+
gr
D
+
+
+
gr-1
gr-1
g1
D
D
Код состояний делителя
g0
D
45. Пример
• Схема деления на полином• g(x) = x6 +x5 +x4 +x3 + 1 над GF(2)
+
…dn-2, dn-1, dn
D
D
D
+
D
+
D
+
D
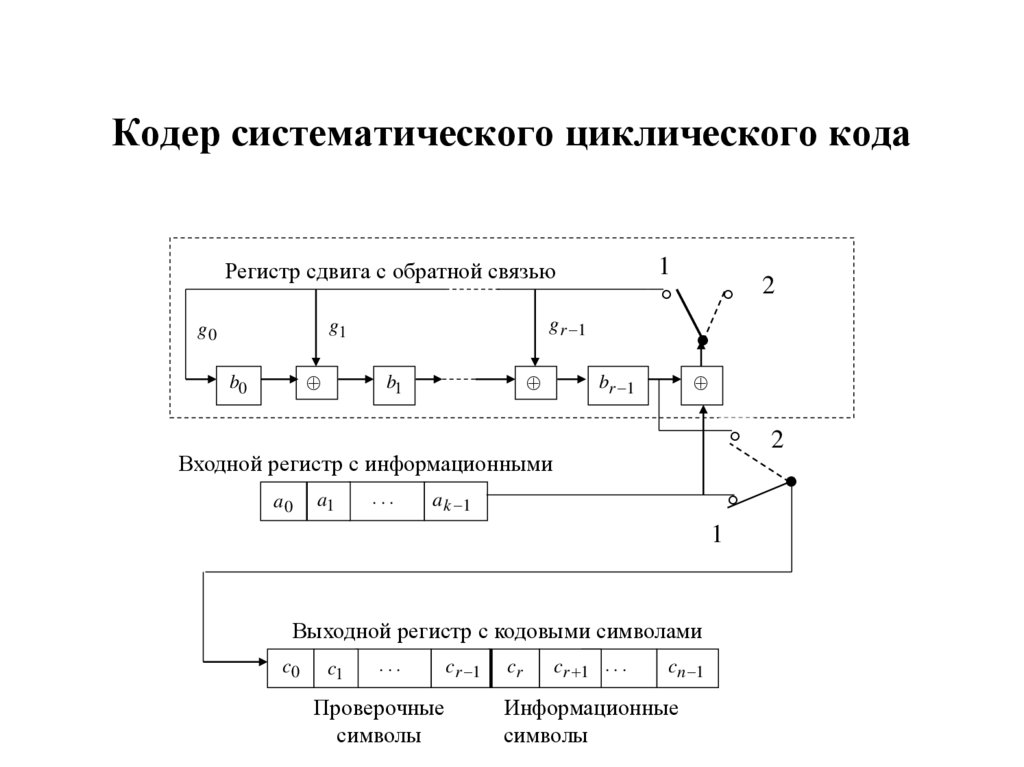
46. Кодер систематического циклического кода
1Регистр сдвига с обратной связью
g r -1
g1
g0
b0
b1
br -1
Входной регистр с информационными
символами
...
a
a
a
0
k -1
1
1
Выходной регистр с кодовыми символами
c0
c1
...
Проверочные
символы
cr -1
cr
2
cr +1 . . .
cn -1
Информационные
символы
2
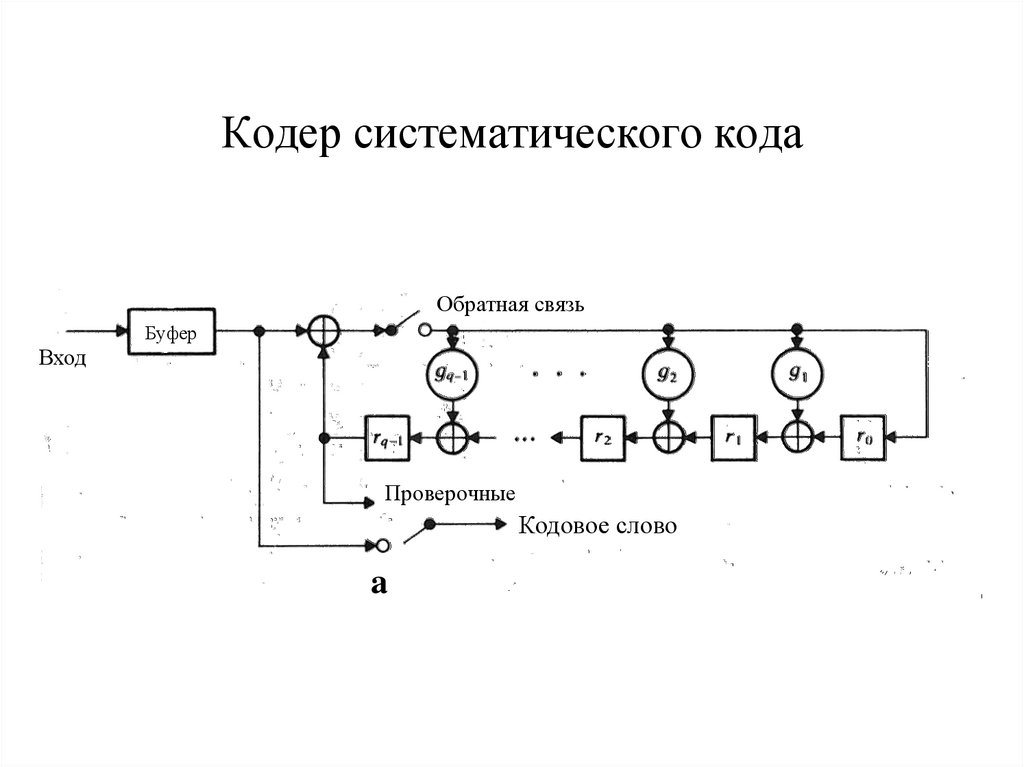
47. Кодер систематического кода
Обратная связьБуфер
Вход
Проверочные
Кодовое слово
a
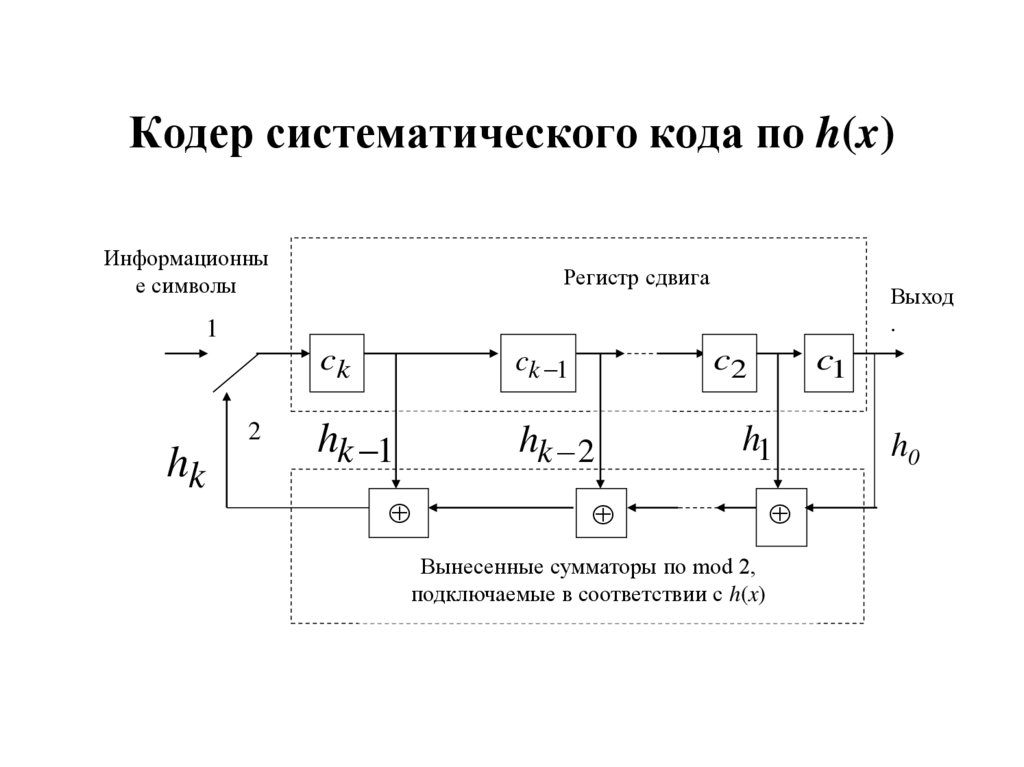
48. Кодер систематического кода по h(x)
Информационные символы
Регистр сдвига
Выход
.
1
2
hk
ck
ck -1
hk -1
hk - 2
c2
c1
h1
Вынесенные сумматоры по mod 2,
подключаемые в соответствии с h(x)
h0
49. Кодирование циклическим кодом путем задания корней всех кодовых полиномов
• Кодирование предполагает переход в соответствующеерасширенное поле GF(pm). Условие, что все кодовые
полиномы делятся на порождающий многочлен g(x),
означает, что все полиномы слов кода должны
принимать нулевое значение на корнях полинома g(x).
50. Кодирование
11
H =
1
n-k
12
n2- k
1n -1
nn--k1
51. Пример
• Пример.Построить
проверочную
матрицу
циклического
кода
с
параметрами (15, 11), используя метод
задания корней кодовых слов.
52. Решение.
• Определим полином f = x15 – 1. Разложимданный полином на множители,
применив оператор:
• > Factor((x^15 – l)) mod 2;
• (x^4 + x + 1)*(x^2 + x + 1)*(x^4 + x^3 +
x^2 + x + 1)*(x^4 + x^3 + 1)*(x + 1)=
• =(x4 + x + 1)(x2 + x + 1)(x4 + x3 + x2 + x +
1)(x4 + x3 + 1)(x + 1).
53.
• Выберем из полученного результатаполином g(x) = (x4 + x + 1).
• Используя оператор irreduc( x^4 + x + 1),
убедимся, что данный полином
неприводимый и может служить в
качестве полинома для построения поля
GF(24).
54.
Определим примитивный элемент поля
> alias (alpha = RootOf(Z^4 + Z + 1) mod 2):
и построим элементы поля
> for i to 2^4-2 do powers[i] := evala (alpha^(i
– 1)) mod p; od:
55.
• Найдем корни полинома (x4 + x + 1) врасширенном поле путем разложения
полинома на элементарные множители:
• > Factor(g, alpha) mod 2;
• (x + alpha + 1)*(x + alpha)*(x + alpha^2 +
1)*(x + alpha^2)
56.
• Таким образом, корнями полинома (x4 +x + 1) являются следующие элементы
поля:
• . = ; = 2 ; = 1 + = 4 ; = 1 + 2 = 8
1
2
3
4
57.
• Используя выражение для H ипредставляя корни как вектор столбцы,
после соответствующих упрощений
получим
1
0
H=
0
0
0 0 0 1 0 0 1 1 0 1 0 1 1 1
1 0 0 1 1 0 1 0 1 1 1 1 0 0
0 1 0 0 1 1 0 1 0 1 1 1 1 0
0 0 1 0 0 1 1 0 1 0 1 1 1 1




















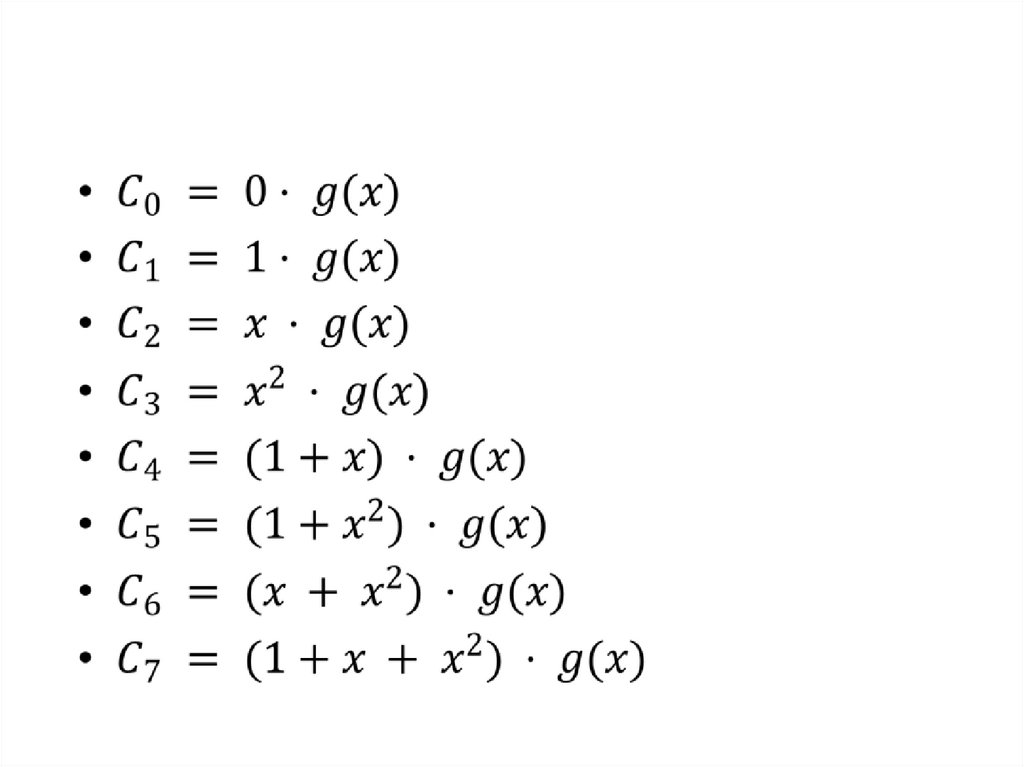




























 informatics
informatics








