Лекция 15. CRC_коды

1. CRC - коды

2. Понятие CRC - кода

Циклические коды или CRC-коды (cyclical redundancy check – избыточные коды
с циклическими проверками) были получены в поисках более простой технической
реализации помехоустойчивого кодирования.
Благодаря хорошим корректирующим свойствам, относительно малой
избыточности, простоте схемной реализации устройств кодирования и
декодирования CRC–коды получили широкое распространение.
Своим названием они обязаны тому, что циклический сдвиг кодовой комбинации
приводит к другой разрешенной кодовой комбинации.
С1С2 ...Сn 1Сn комбинация CRC - кода, то и
Если
С1 С2 ... Сn 1 C n
C2 C3 ... Cn C1
C3 C4 ... C1 C 2
разрешенные комбинации этого кода.
CRC–коды относятся к систематическим кодам:
информационные занимают k старших разрядов n –разрядной комбинации,
проверочные – m=n-k младших разрядов.

3. Математическое описание CRC - кодов

При описании CRC–кодов n–разрядные кодовые комбинации представляются в
виде полиномов степени (n-1) фиктивной (не несущей смысловой нагрузки)
переменной x:
V( x ) C n 1x n 1 C n 2 x n 2 ... C0 x 0
C n i– коэффициенты, принимающие значение i-ых разрядов описываемой кодовой
комбинации. Для двоичных циклических кодов Ñi 0,1 , а описывающие такие
коды полиномы называют двоичными.
Например, кодовой комбинации
C6C5C4C3C2C1C0 1001101
соответствует полином
V(x ) 1 x 6 0 x 5 0 x 4 1 x 3 1 x 2 0 x1 1 x 0 x 6 x 3 x 2 1
Однозначное соответствие между кодовыми комбинациями и описывающими их
полиномами позволяет свести действия над комбинациями к действиям над
полиномами.

4. Операции над двоичными полиномами

Над двоичными полиномами можно выполнять все алгебраические
операции, причем:
коэффициенты при одинаковых степенях переменной x складываются по
модулю два (без переноса в старший разряд),
операция вычитания эквивалентна сложению.
Следует обратить внимание на операцию умножения на полином степени m:
Она соответствует сдвигу кодовой комбинации на m разрядов в сторону
старших.
Пример: Пусть m=3 и полином V( x ) x 3 x 2 1 умножается на x3.
Полиному V( x ) x 3 x 2 1
соответствует комбинация 1101.
Полиному V( x ) ( x 3 x 2 1) x 3 x 6 x 5 x 3 - комбинация 1101000.

5. Свойства CRC - кода

Основное свойство CRC–кодов: все полиномы V( x ) , представляющие
кодовые комбинации CRC–кода, делятся без остатка на полином G m ( x ) степени
m, который называется образующим или производящим полиномом.
Степень полинома равна числу проверочных символов m = n-k.
В качестве G m ( x ) используется неприводимые полиномы, т.е. такие, которые
делятся без остатка только на единицу и на себя.
Неприводимые полиномы играют роль, сходные с простыми числами в
теории чисел. Вид неприводимого полинома зависит от числа проверочных
символов m. Имеются таблицы неприводимых полиномов. Некоторые из
полиномов представлены в таблице 1.1.
Свойства делимости комбинации CRC – кода на образующий полином
положено в основу циклического кодирования и декодирования.

6. Таблица неприводимых полиномов

m
Gm (x)
Двоичный
эквивалент
3
1
G1 ( x) x 1
11
2
G2 ( x) x 2 x 1
111
3
4
Десятичный
эквивалент
7
G3 ( x) x 3 x 1
1011
11
G3 ( x) x 3 x 2 1
1101
13
G4 ( x ) x 4 x 1
10001
17
G4 ( x ) x 4 x 3 1
11001
25
G4 ( x ) x 4 x 3 x 2 x 1
11111
31

7. Кодирование (1)

Под кодированием понимается преобразование безызбыточной k– разрядной
комбинации в n = k+m–разрядную комбинацию CRC–кода.
На практике широко используется кодирование по методу деления на образующий
полином, согласно которому выполняется следующие операции:
1.
Подлежащая кодированию безызбыточная k–разрядная кодовая комбинация
описывается полиномом Ck (x) степени (k-1).
2.
Полином Ck (x) умножается на xm, что эквивалентно сдвигу безызбыточной kразрядной комбинации влево (в сторону старших разрядов), на m разрядов или
добавлению m нулей справа.
3.
Полученный полином Ck (x) xm делится на образующий полином Gm(x), имеющий
степень, равную числу проверочных символов m, в результате чего получается целая
часть Q(x) и остаток деления R(x):
C k (x)x m
R (x)
Q( x )
.
G m (x)
G m (x)
4.
(*)
Формируется n–разрядная комбинация CRC–кода, описываемая полиномом:
Vn ( x) Ck (x) x m R ( x),
для чего в освободившиеся при сдвиге по п.2 разряды записывается комбинация,
соответствующая остатку R(x).

8. Кодирование (2)

Покажем, что комбинации, соответствующие полиному Vn ( x ), являются
разрешенными:
Умножим обе части уравнения (*) на Gm(x):
Ck (x)x m Q(x)G m ( x) R ( x)
Вычитая из обеих частей R(x) и учитывая, что операция вычитания и суммирования по
mod2 эквивалентны, получим:
Ck (x)x m R (x) Q(x)G m ( x)
Выражение в левой части этого равенства - это полиномVn ( x ) . Следовательно
Vn ( x )
Q( x ) - целая часть,
G m (x)
т.е. полученный полином Vn ( x ) делится на Gm(x) без остатка, а значит
представляет разрешенную комбинацию циклического кода (на основании основного
свойства циклического кода).

9. Кодирование (3)

Пример. Закодируем безызбыточную кодовую комбинацию 1001 CRC-кодом с
образующим полиномом G( x ) x 3 x 1 .
Число информационных символов k=4, проверочных m = 3. Общая длина
комбинации n=7 . В соответствии с рассмотренным методом кодирования получаем:
1.
1001 C4 ( x) x3 1
2.
C4 ( x ) x 3 x 6 x 3
3.
4.
V7 ( x) C4 ( x) x 3 R( x) x 6 x 3 x 2 x 1001110

10. Кодирование (4)

Все операции кодирования можно выполнять непосредственно над кодовыми
комбинациями.
Пример:

11. Декодирование (1)

Декодирование сводится к обнаружению или исправлению ошибок (в
зависимости от поставленной задачи и величины кодового расстояния). Обнаружение
ошибок
Процедура обнаружения ошибки сводится к делению принятой комбинации на
образующий полином и анализу остатка от деления :
Если R ( x ) =0, то ошибок нет (разрешенные кодовые комбинации делятся на
образующий полином без остатка) или произошел прием с необнаруживаемой
ошибкой (под действием искажений одна разрешенная комбинация перешла в другую
разрешенную комбинацию).
Если R ( x ) ≠0, то произошел прием с ошибкой (обнаруживаемой).
Остаток играет роль синдрома в коде Хэмминга.

12. Декодирование (2)

Пример: Пусть полученная комбинация 1001110 совпадает с
переданной, т.е. искажений нет. Известно, что комбинация
образована с помощью образующего полинома G3(x)=x3+x2+1. В
результате деления полинома, описывающего эту комбинацию на
образующий полином G3(x) получаем:

13. Декодирование (3)

Пусть для тех же условий искажен искажен 2-ой символ, т.е. принята
комбинация 1101110.
Тогда

14. Декодирование (5)

Исправление однократных ошибок
Определение места ошибки в принятой комбинации CRC–кода основано на
'
анализе остатка R ( x ) от деления полинома Vn ( x ) принятой комбинации на
образующий полином G m ( x ).
Принятую с ошибкой в i-м разряде n-разрядную кодовую комбинацию CRC –кода
можно представить полиномом:
Vn' ( x) Vn (x) x n i
где
i 1, n – номер искаженного разряда;
Vn(x) – полином комбинации CRC–кода, принятой без ошибки;
x n i – полином однократной ошибки (ошибку можно представить как n – разрядную
комбинацию с «1» в i-м разряде; например, при i =2 и n=5 ошибка представляется
комбинацией 01000, которой соответствует полином x3).
'
После деления Vn ( x ) на G m ( x ) получим
Vn' ( x) Vn ( x)
x n i
Gm ( x) Gm ( x) Gm ( x)

15. Декодирование (6)

Согласно свойству CRC–код Vn ( x ) делится на G m ( x ) без остатка.
n i
Остаток от деления Vn' ( x ) на G m (x) равен остатку от деления x
, т.е. не
зависит от вида Vn ( x) , а определяется только положением принятого с ошибкой
символа. Это позволяет определить место ошибки путем деления
последовательно сдвигаемой принимаемой комбинации в сторону старшего
разряда* и сравнения остатков R j ( x ), j 0, n 1 (j-число сдвигов) от деления
'
сдвигаемой комбинации с остатком R0 ( x ) (выделенным синдромом) от
n 1
деления на полином G m ( x ), полинома x
, описывающего ошибку в
старшем разряде.
Согласно одному из методов исправления однократных ошибок при
'
совпадении остатков R j (x) R 0 (x) на j-ом шаге принимается решение об
искажении символа C j 1 , номер которого на единицу больше числа сдвигов j.
* - циклический сдвиг разрешенной комбинации приводит к разрешенной комбинации

16. Декодирование (7)

Пример. Пусть комбинация CRC–кода (7,4) 1001110, сформированная с
помощью образующего полинома G( x) x3 x 1 принята с ошибкой в третьем
разряде: 1011110.
Для исправления ошибки находим выделенный синдром R '0 ( x ) , выполняя
деление полинома ошибки в старшем разряде x 6 на образующий полином в
двоичном эквиваленте:

17. Декодирование (8)

Находим остатки от деления принятой кодовой комбинации на двоичный
эквивалент образующего полинома, сдвигая принимаемую комбинацию влево
до тех пор, пока остаток не совпадет с выделенным синдромом R j (x) R '0 (x) :
Остаток совпал после сдвига j=2. Следовательно искажен разряд Сj+1=С3.

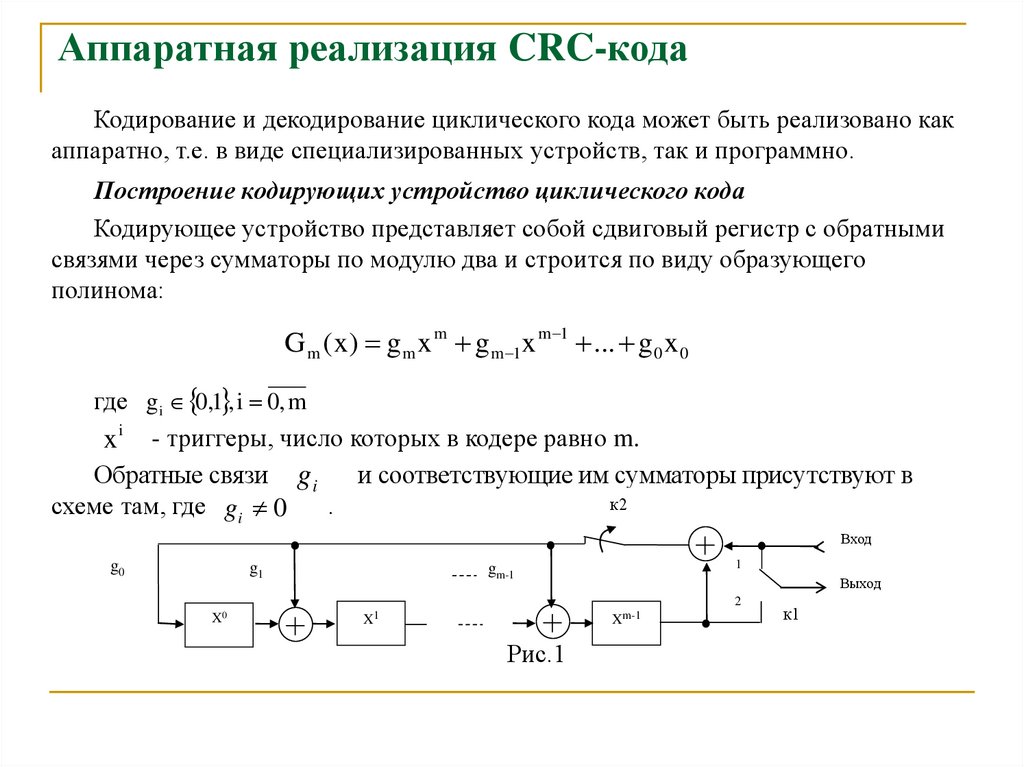
18. Аппаратная реализация CRC-кода

Кодирование и декодирование циклического кода может быть реализовано как
аппаратно, т.е. в виде специализированных устройств, так и программно.
Построение кодирующих устройство циклического кода
Кодирующее устройство представляет собой сдвиговый регистр с обратными
связями через сумматоры по модулю два и строится по виду образующего
полинома:
G m ( x ) g m x m g m 1x m 1 ... g 0 x 0
где g i 0,1 , i 0, m
x i - триггеры, число которых в кодере равно m.
Обратные связи g i
и соответствующие им сумматоры присутствуют в
к2
схеме там, где g i 0
.
Вход
g0
g1
1
gm-1
Выход
2
X0
X1
Xm-1
Рис.1
к1

19. Аппаратная реализация CRC-кода

Кодирование сводится к формированию в регистре m проверочных символов.
x 0 x m 1 – в нулевом состоянии,
Перед началом кодирования триггеры
ключ k1 – в положении «1», k2 – замкнут. Кодируемая безызбыточная k – разрядная
комбинация поступает символ за символом в схему и одновременно через ключ k1
на выход кодера. Первым в этой последовательности идет символ старшего разряда.
С приходом последнего k-го информационного символа формирование
проверочных символов в КУ заканчивается, ключ k2 размыкается, ключ k1
переключается в положении «2» и сформированные в регистре проверочные
символы поступают на выход вслед за информационными, что обеспечивается
путем последовательного сдвига сформированной в регистре комбинации
проверочных символов.

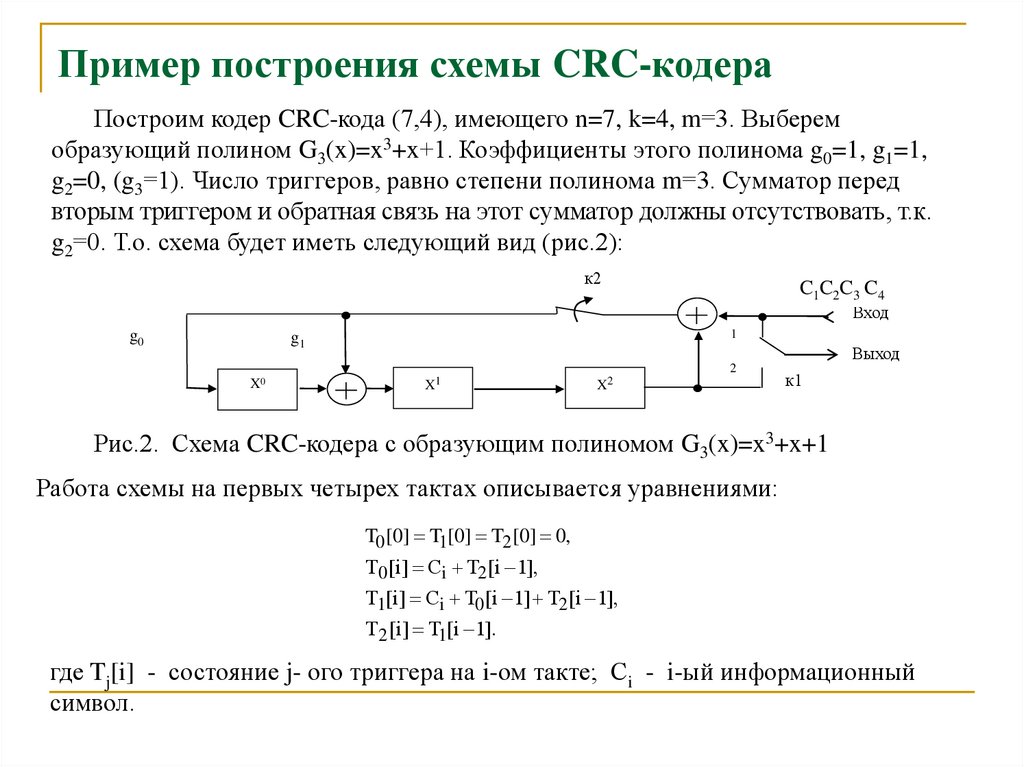
20. Пример построения схемы CRC-кодера

Построим кодер CRC-кода (7,4), имеющего n=7, k=4, m=3. Выберем
образующий полином G3(x)=x3+x+1. Коэффициенты этого полинома g0=1, g1=1,
g2=0, (g3=1). Число триггеров, равно степени полинома m=3. Сумматор перед
вторым триггером и обратная связь на этот сумматор должны отсутствовать, т.к.
g2=0. Т.о. схема будет иметь следующий вид (рис.2):
к2
C1C2C3 C4
Вход
g0
1
g1
Выход
2
X0
X1
X2
к1
Рис.2. Схема CRC-кодера с образующим полиномом G3(x)=x3+x+1
Работа схемы на первых четырех тактах описывается уравнениями:
T0 [0] T1[0] T2 [0] 0,
Т 0 [i] Ci T2 [i 1],
Т1[i] Ci T0 [i 1] T2 [i 1],
Т 2 [i] T1[i 1].
где Tj[i] - состояние j- ого триггера на i-ом такте; Сi - i-ый информационный
символ.

21. Аппаратная реализация CRC-кода

Работу кодера проиллюстрируем на примере кодирования безызбыточной
комбинации C1C2C3 C4 = 1001.
Составим таблицу состояний кодера, отражающую состояния кодера на всех
тактах процесса кодирования. Это можно сделать непосредственно по схеме кодера
или по уравнениям, описывающим его работу.

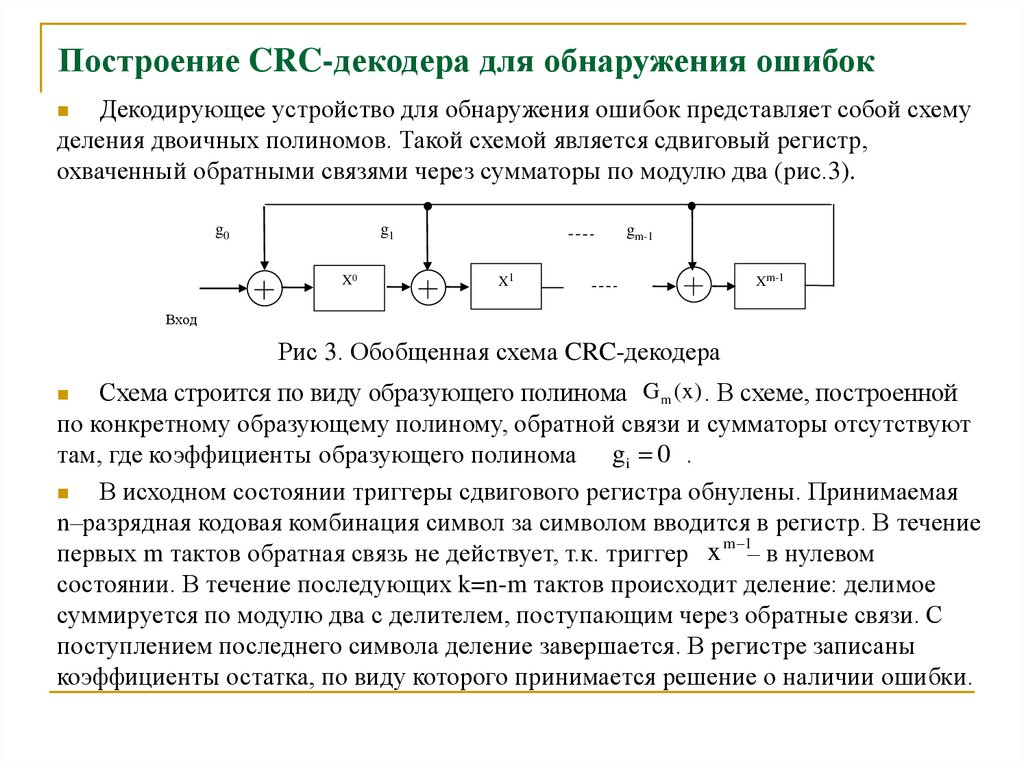
22. Построение CRC-декодера для обнаружения ошибок

Декодирующее устройство для обнаружения ошибок представляет собой схему
деления двоичных полиномов. Такой схемой является сдвиговый регистр,
охваченный обратными связями через сумматоры по модулю два (рис.3).
g1
g0
X0
gm-1
X1
Xm-1
Вход
Рис 3. Обобщенная схема CRC-декодера
Схема строится по виду образующего полинома G m (x) . В схеме, построенной
по конкретному образующему полиному, обратной связи и сумматоры отсутствуют
там, где коэффициенты образующего полинома gi 0 .
В исходном состоянии триггеры сдвигового регистра обнулены. Принимаемая
n–разрядная кодовая комбинация символ за символом вводится в регистр. В течение
m 1
первых m тактов обратная связь не действует, т.к. триггер x – в нулевом
состоянии. В течение последующих k=n-m тактов происходит деление: делимое
суммируется по модулю два с делителем, поступающим через обратные связи. С
поступлением последнего символа деление завершается. В регистре записаны
коэффициенты остатка, по виду которого принимается решение о наличии ошибки.

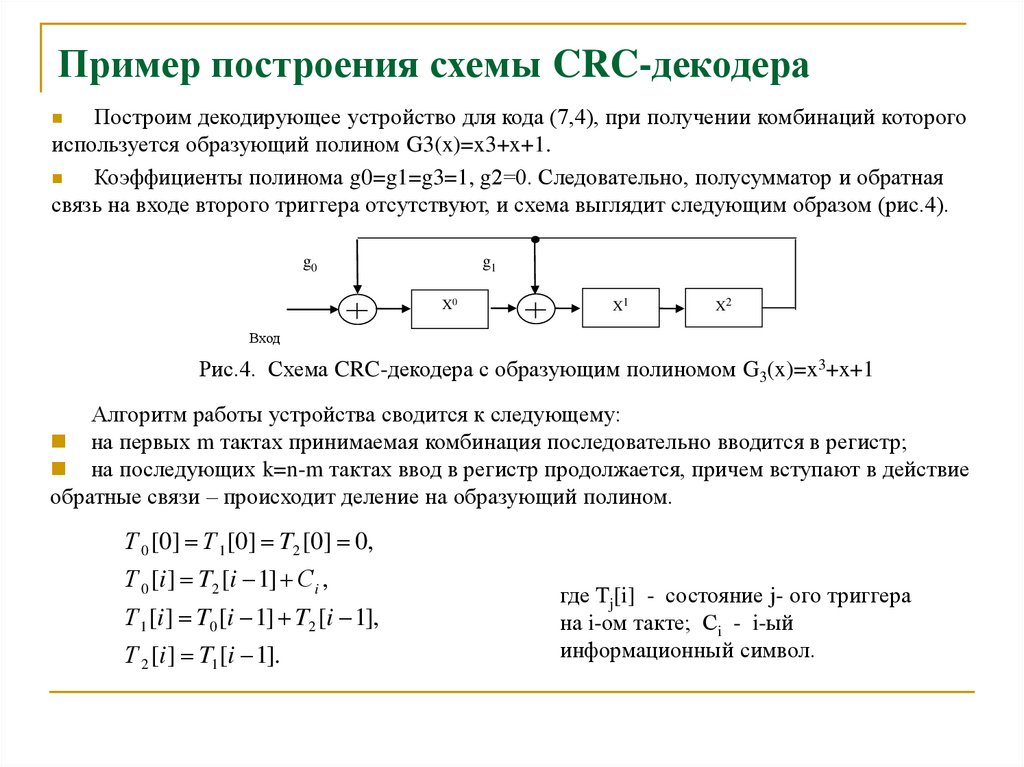
23. Пример построения схемы CRC-декодера

Построим декодирующее устройство для кода (7,4), при получении комбинаций которого
используется образующий полином G3(x)=x3+x+1.
Коэффициенты полинома g0=g1=g3=1, g2=0. Следовательно, полусумматор и обратная
связь на входе второго триггера отсутствуют, и схема выглядит следующим образом (рис.4).
g1
g0
X0
X1
X2
Вход
Рис.4. Схема CRC-декодера с образующим полиномом G3(x)=x3+x+1
Алгоритм работы устройства сводится к следующему:
на первых m тактах принимаемая комбинация последовательно вводится в регистр;
на последующих k=n-m тактах ввод в регистр продолжается, причем вступают в действие
обратные связи – происходит деление на образующий полином.
Т 0 [0] Т 1 [0] T2 [0] 0,
Т 0 [i ] T2 [i 1] Сi ,
Т 1 [i ] T0 [i 1] T2 [i 1],
Т 2 [i ] T1 [i 1].
где Tj[i] - состояние j- ого триггера
на i-ом такте; Сi - i-ый
информационный символ.

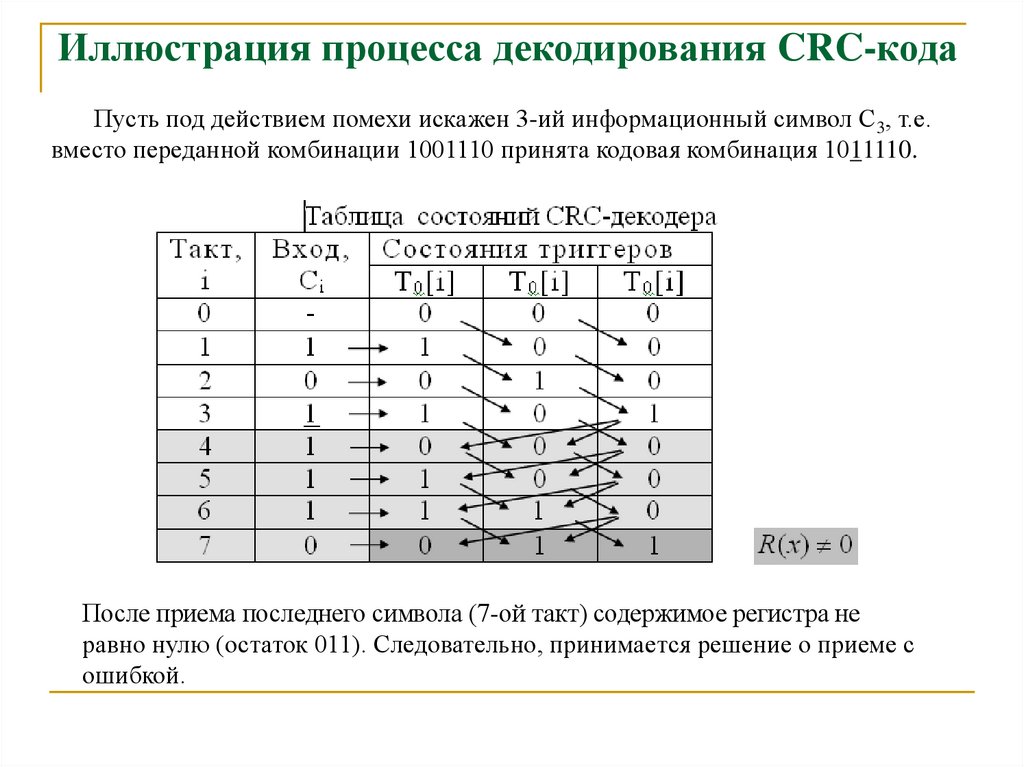
24. Иллюстрация процесса декодирования CRC-кода

Работу декодера проиллюстрируем на примере декодирования принимаемой
комбинация 1001110. Пусть в ней нет ошибок .
Т 0 [0] Т 1 [0] T2 [0] 0,
Т 0 [i ] T2 [i 1] Сi ,
Т 1 [i ] T0 [i 1] T2 [i 1],
Т 2 [i ] T1 [i 1].
После завершения приема кодовой комбинации все триггеры находятся в
нулевом состоянии. Следовательно, остаток R(x)=0 и ошибок нет.

25. Иллюстрация процесса декодирования CRC-кода

Пусть под действием помехи искажен 3-ий информационный символ С3, т.е.
вместо переданной комбинации 1001110 принята кодовая комбинация 1011110.
После приема последнего символа (7-ой такт) содержимое регистра не
равно нулю (остаток 011). Следовательно, принимается решение о приеме с
ошибкой.

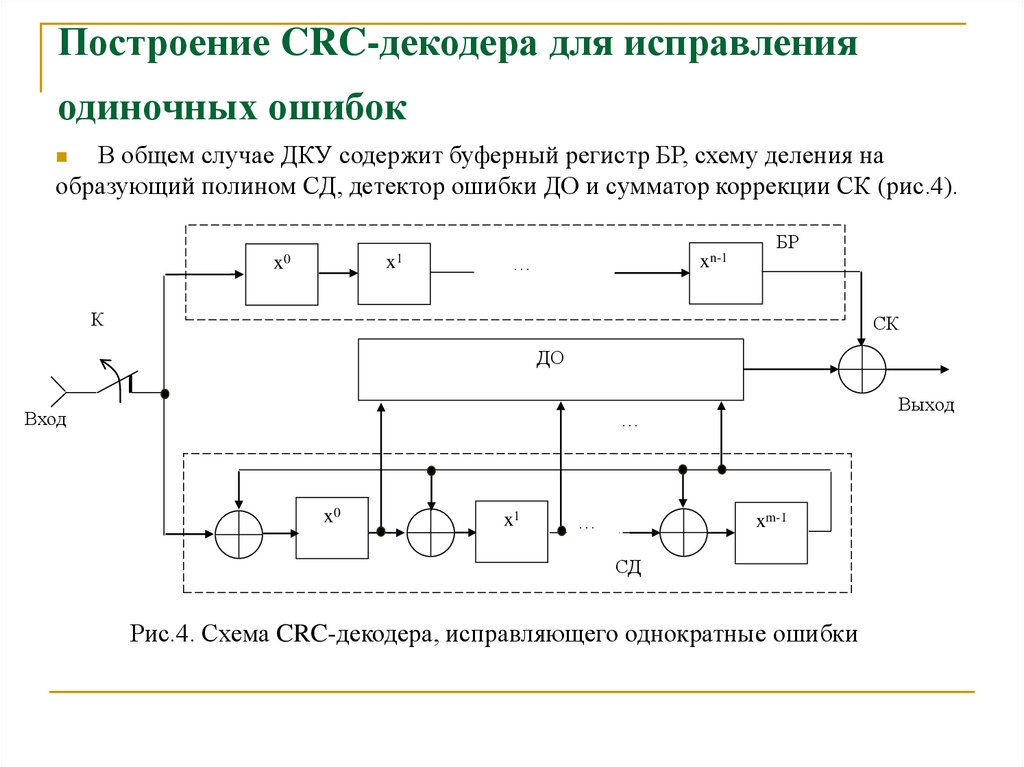
26. Построение CRC-декодера для исправления одиночных ошибок

В общем случае ДКУ содержит буферный регистр БР, схему деления на
образующий полином СД, детектор ошибки ДО и сумматор коррекции СК (рис.4).
БР
x1
x0
…
xn-1
К
СК
ДО
Вход
Выход
…
x0
x1
…
xm-1
СД
Рис.4. Схема CRC-декодера, исправляющего однократные ошибки

27. Работа CRC-декодера при исправлении одиночных ошибок

Декодирование осуществляется за 2n тактов.
В течение первых n тактов кодовая комбинация записывается в БР, а в СД
формируется остаток R 0 ( x ) от деления принимаемой комбинации на образующий
полином G m ( x ) .
Исправление происходит в течение последующих n тактов, когда в БР
продолжаются сдвиги. При этом искаженный разряд перемещается к выходу БР, а в
СД продолжается деление сдвигаемой комбинации (ключ «К» разомкнут, и на вход
СД поступают «нули»), и на ДО, представляющий собой логическую схему,
настроенную на выделенный синдром R '0 ( x ) , поступают остатки R j ( x ) . В
момент, когда ошибка окажется в старшем n-м разряде БР, на выходе СД образуется
выделенный синдром, ДО выдает сигнал «1», который поступает на СК, изменяя
значения очередного символа, поступающего на СК с выхода БР. Ошибка
исправляется.
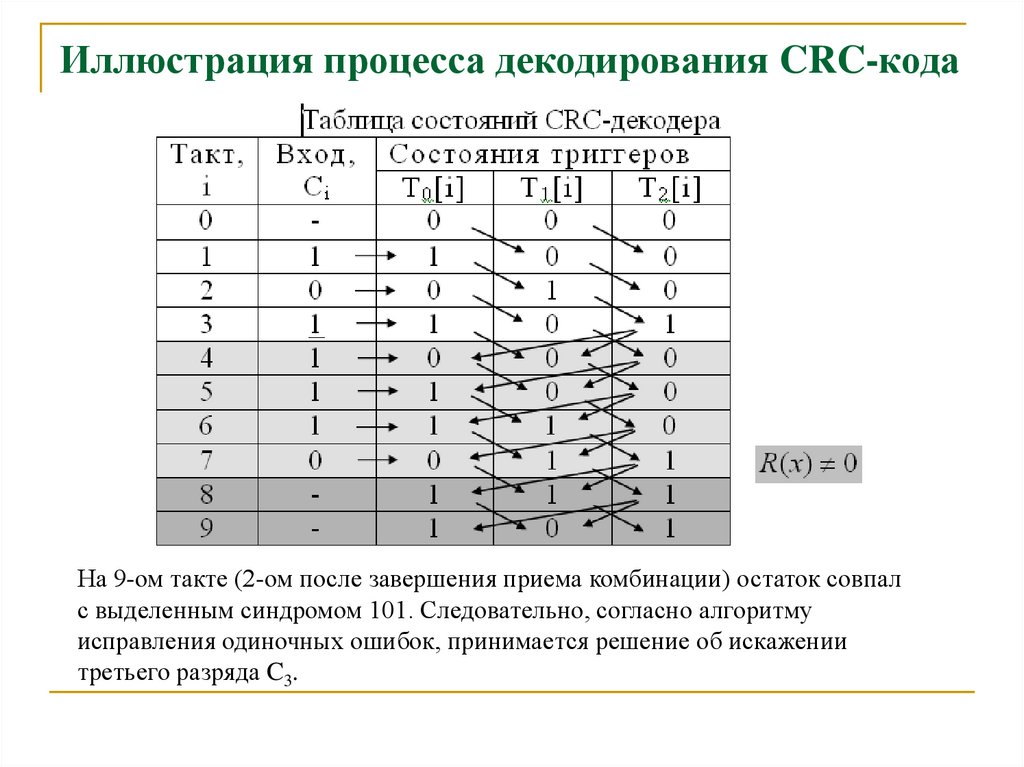
Проиллюстрируем работу декодера с помощью табл. 5.3 состояний для
условий примера 2.

28. Иллюстрация процесса декодирования CRC-кода

На 9-ом такте (2-ом после завершения приема комбинации) остаток совпал
с выделенным синдромом 101. Следовательно, согласно алгоритму
исправления одиночных ошибок, принимается решение об искажении
третьего разряда C3.

29. Аналитическое оценивание эффективности (n,k)-кодов

Эффективность корректирующего кода характеризуется вероятностями:
Pnn - правильного приема кодовой комбинации,
Poo - обнаруживаемой ошибки,
Pно - необнаруживаемой ошибок.
Для этих вероятностей справедливо соотношение:
Pnn Poo Pно 1.
Для сравнения эффективности кодов пользуются коэффициентом повышения
достоверности, который определяется для режима обнаружения и исправления следующим
образом:
P( 1, n)
P( 1, n )
и
.
0
,
P(
1,
n)
P
P( 1, n ) Poo
ио
P( 1, n )
- вероятность появления одной и более ошибок в n – разрядной кодовой
комбинации; Poo - вероятность обнаружения ошибки; Pио - вероятность исправления ошибки.
Коэффициент показывает, во сколько раз, применяемый корректирующий код
уменьшает вероятность того, что выданная получателю комбинация будет содержать
ошибку по сравнению с безызбыточным кодом той же разрядности.

30. Аналитическое оценивание эффективности (n,k)-кодов

Рассмотрим расчет эффективности кода (7,4).
Такой код имеет:
d min 3 ,
минимальное кодовое расстояние
позволяет обнаруживать все ошибки кратности q o d min 1, т.е. q o 2,
(d
1)
исправлять ошибки кратности qи min2 , т.е. qи 1 .
Полагая, что ошибки независимы и возникают с вероятностью p, т.е.
математическая модель ошибок – биноминальный закон распределения, согласно
которому вероятность искажения t символов в n – разрядной комбинации равна
n
P( t , n ) p t (1 p) n t ,
t
n
n!
- биноминальные коэффициенты, можно рассчитать показатели
где t
t!(n t )! эффективности для режима обнаружения и исправления ошибки
следующим образом.

31. Аналитическое оценивание эффективности (n,k)-кодов

Рассмотрим расчет эффективности кода (7,4).
Такой код имеет
d min 3 ,
минимальное кодовое расстояние
Позволяет:
обнаруживать все ошибки кратности q o d min 1, т.е. q o 2 ,
(d
1)
исправлять ошибки кратности qи min , т.е. qи 1 .
2
Полагая, что ошибки независимы и возникают с вероятностью p, т.е.
t
математическая модель ошибок – биноминальный
закон распределения, согласно
которому вероятность искажения
символов в n – разрядной комбинации равна
n
P( t , n ) p t (1 p) n t ,
t
n
n!
- биноминальные коэффициенты, можно рассчитать показатели
где
t
t
!
(
n
t
)!
эффективности для режима обнаружения и исправления ошибки
следующим образом.

32. Режим обнаружения ошибок (1)

33. Режим обнаружения ошибок (2)

34. Режим исправления ошибок