Similar presentations:
Основы теории линейного программирования Виды задач линейного программирования Общая задача линейного программирования (ЗЛП)
1.
Основы теории линейного программированияВиды задач линейного программирования
Общая задача линейного программирования (ЗЛП).
Необходимо найти вектор x = ( x1, x2, …, xn ) D Rn
C ( x) c1 x1 c2 x2 ... cn xn max (min)
при
выполнении
ограничений:
следующих
непрямых
(1)
(структурных)
2.
a11 x1 a12 x 2 ... a1n x n R1 b1a x a x ... a x R b
21 1
22
2
2n
n
2
2
..........................................................
a m1 x1 a m 2 x 2 ... a mn x n Rm bm
(2)
и прямых ограничений на переменные:
j xj j,
j 1, n
Ri – один из возможных знаков отношений
Ri , ,
,
i 1, m,
(3)
3.
cj , bi , aij – заданные вещественные числа, i 1, m;j 1, n
Числа сj – коэффициенты целевой функции;
элементы aij – коэффициенты матрицы ограничений;
числа bi – правые части системы ограничений.
Границы изменения переменных αj и βj произвольные
вещественные числа, j – , j + .
Цель решения ЗЛП (1) – (3) найти оптимальный план задачи,
т.е. такого плана, на котором достигается наибольшее (или
наименьшее) значение целевой функции (1).
4.
Производственная задача.Предприятие может изготавливать n видов продукции,
используя m видов ресурсов, запасы которых ограничены.
Прибыль от реализации каждого вида продукции,
различна. Нормативный расход i-го ресурса,
затрачиваемого на производство единицы продукции j-го
вида, составляет aij , i 1, m; j 1, n
Запасы ресурсов каждого вида: bi . Прибыль от
реализации единицы продукции j-го вида: сj денежных
единиц.
5.
xj количество единиц продукции j-го вида, j 1, n ,запланированных к производству. Тогда прибыль:
С ( x) с1 x1 с2 x2 ... сn xn max
(4)
n
Для изготовления всей продукции потребуется
a
j 1
ij
xj
единиц ресурса i-го вида.
Т.к. запас i-го ресурса не превосходит величины bi , i 1, m
значит, имеем систему ограничений:
a11 x1 a12 x 2 ... a1n x n b1
a x a x ... a x b
21 1
22
2
2n
n
2
.........................................................
a m1 x1 a m 2 x 2 ... a mn x n bm
(5)
6.
Выпуск продукции не может быть отрицательным:x j 0,
j 1, n
(6)
Построенная экономико-математическая модель (4), (5), (6)
называется многопродуктовой моделью производственного
планирования.
7.
Пусть на предприятии выпускается один продукт разнымитехнологическими способами. Количество технологических
способов: n. аij характеризуют нормативный расход i-го вида
ресурса при применении j-го технологического способа с
единичной интенсивностью. bi - наличие i-го ресурса, а cj –
прибыль от реализации единицы продукции произведенной
j-м способом,
i 1, m;
j 1, n
8.
Экономико-математическая модель этой задачи будетидентична модели (4), (5), (6). Но в этом случае она будет
являться однопродуктовой моделью производственного
планирования.
При этом модель (4), (5), (6) представляет собой
стандартную форму записи задачи линейного
программирования (ЗЛП).
9.
Характеристика стандартной формы записи ЗЛП:1. Целевая функция стремится к максимуму.
2. Все непрямые (структурные) ограничения имеют знаки
отношений «меньше-равно» ( ≤ ).
3. Все переменные неотрицательны,x j 0,
j 1, n
10.
а11а 21
А
...
а
m1
а12
а 22
...
аm2
... а1n
... а 2 n
... ...
... а mn
с (с1 , с2 ,..., сn )
– технологическая матрица
коэффициентов
– вектор удельной прибыли от
реализации продукции
b1
b2
b
...
b
m
– вектор запасов ресурсов
11.
x1x2
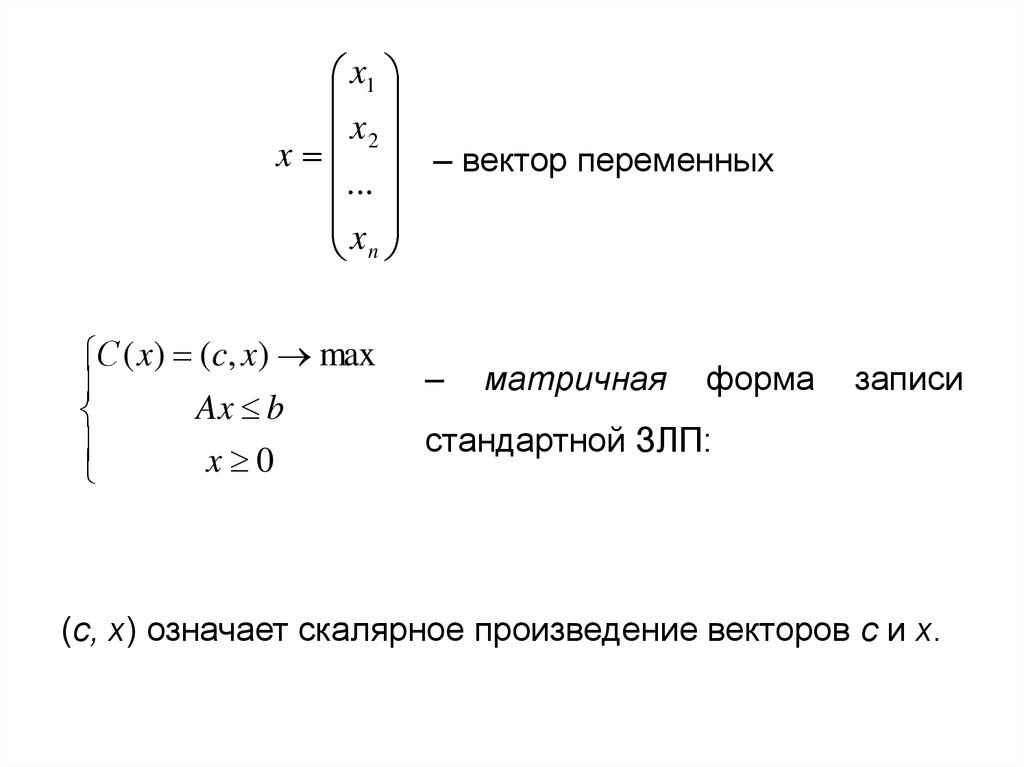
x – вектор переменных
...
x
n
С ( x) (c, x) max
Ax b
x 0
–
матричная
форма
записи
стандартной ЗЛП:
(c, x) означает скалярное произведение векторов c и x.
12.
Векторная форма записи стандартной ЗЛП получится, есливведем обозначение векторов матрицы системы
ограничений
a1 j
a2 j
Aj
,
......
a
mj
C ( x) (c, x) max
A1 x1 A2 x2 ... An xn b
x , x ,..., x 0
n
1 2
j 1, n
– векторная форма записи
стандартной ЗЛП
13.
Общая ЗЛП может быть легко сведена к стандартнойформе записи при помощи четырех действий:
1. Структурные ограничения типа ≥ в общей ЗЛП
заменяются на ограничения типа путем их
умножения на (-1).
2. Структурные ограничения типа = в общей ЗЛП
заменяются на неравенства типа с помощью
вычитания из левой части равенств вновь введенных
неотрицательных переменных.
14.
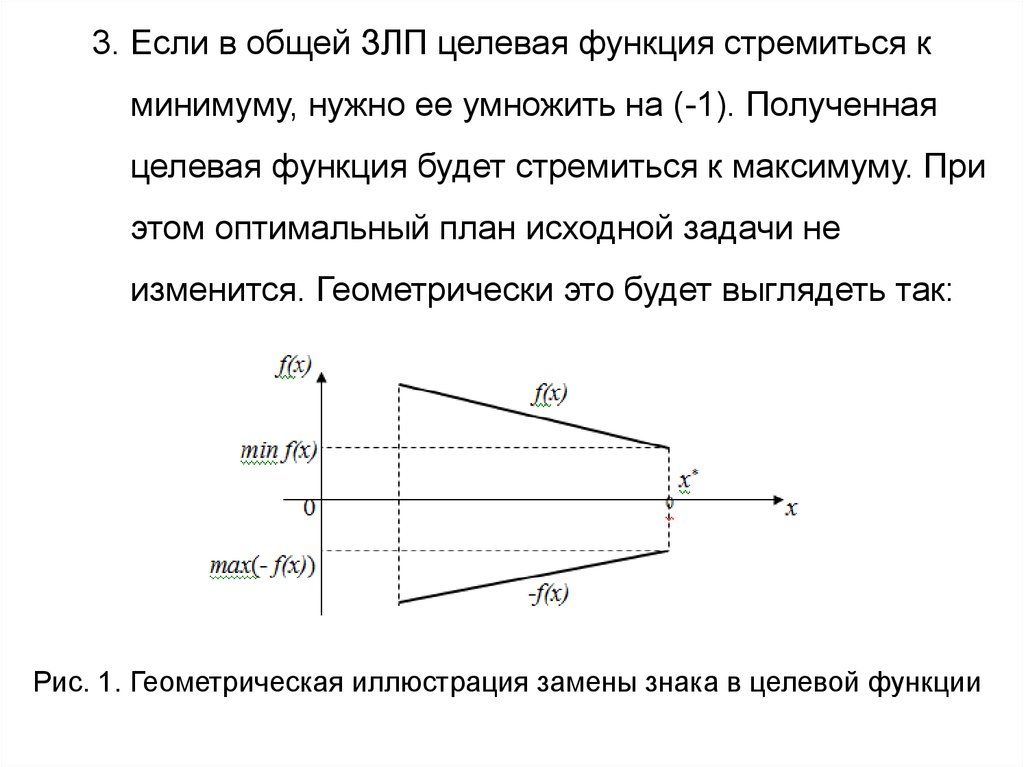
3. Если в общей ЗЛП целевая функция стремиться кминимуму, нужно ее умножить на (-1). Полученная
целевая функция будет стремиться к максимуму. При
этом оптимальный план исходной задачи не
изменится. Геометрически это будет выглядеть так:
Рис. 1. Геометрическая иллюстрация замены знака в целевой функции
15.
4. В стандартной форме записи ЗЛП переменныенеотрицательные. Поэтому, если в общей ЗЛП
переменная xs не определена по знаку, то вводятся
две новые неотрицательные переменные xs1 и xs2 .
Тогда переменная xs представляется как разность этих
двух новых переменных
x s1 0, x s 2 0;
x s x s1 x s 2
16.
П р и м е р.C ( x) 4 x1 6 x 2 2 x3 min
15
x1 10 x 2
3 x 7 x
4
1
2
2 x1 x 2 x3 12
x1 , x 2 0
Введем две новые неотрицательные переменные
x3' 0 и
x3'' 0
и выразим через них x3
x3 x3' x3''
17.
Вычтем из второго ограничения переменную x4 0 иумножим третье ограничение на (-1).
Тогда стандартная форма записи ЗЛП:
C1 ( x) 4 x1 6 x2 2( x3' x3'' ) max
x1 10 x2 15
3 x1 7 x2 x4 4
'
''
2
x
x
x
x
1
2
3
3 12
x1 , x2 , x3' , x3'' , x4 0
18.
Каноническая форма записи ЗЛП имеет следующий вид:С ( x) с1 x1 с2 x2 ... сn xn max
a11 x1 a12 x 2 ... a1n x n b1
a x a x ... a x b
21 1
22
2
2n
n
2
.........................................................
a m1 x1 a m 2 x 2 ... a mn x n bm
x j 0,
j 1, n
(7)
(8)
(9)
19.
Характеристика канонической формы записи ЗЛП:1. Целевая функция стремится к максимуму.
2. Непрямые (структурные) ограничения имеют знаки
отношений «равно».
3. Все переменные неотрицательны.
20.
В канонической ЗЛП всегда число ограничений строгоменьше числа переменных, m n. Это связано со
следующими обстоятельствами:
а) если m = n, то каноническая ЗЛП как задача
оптимизации теряет смысл, поскольку, если она имеет
решение, то это решение единственное.
б) если m n , то система уравнений переопределена
и не имеет решения.
21.
Сведение стандартной формы ЗЛП к канонической.n
а
j 1
ij
x j bi , i 1, m
(10)
Введем дополнительную переменную xn+i :
n
xn i bi aij x j
(11)
j 1
Из (10) следует, что xn+i 0. С учетом (11) выражение (10)
превращается в равенство
n
a
j 1
ij
x j xn i bi , i 1, m
22.
a11 ,..., a1n , 1, 0,..., 0a 21 ,..., a 2 n , 0, 1,..., 0
A
a ,..., a , 0, 0,..., 1
mn
m1
- матрица коэффициентов
системы
Введение дополнительных переменных в стандартную
форму ЗЛП преобразовывает ЗЛП (12) в ЗЛП (13).
(c, x) max
Ax b
x 0
(12)
(1.12)
(с, x) max
A x b
x 0
(13)
(1.13)
23.
x = ( x1, x2,…, xn ) – вектор переменных задачи (12);x ( x1 , x2 ,..., xn , xn 1 , xn 2 ,..., xn m )
– вектор переменных
ЗЛП (13)
Основные переменные Дополнительные переменные
с (с1 , с2 ,..., сn , 0, 0,..., 0) –
вектор
коэффициентов
целевой функции ЗЛП (13).
Каноническая ЗЛП включает m уравнений и N = m+ n
неизвестных. Дополнительные переменные xn+1 , xn+2 ,…,
xn+m рассматриваются наравне с основными
переменными.
24.
Основные определенияРассмотрим ЗЛП в стандартной форме (14) и ЗЛП в
канонической форме (15).
С ( x) (c, x) max
Ax b
x 0
(14)
С ( x) (c, x) max
Ax b
x 0
(15)
Опр.1 Множество векторов D x ( x1 , x2 ,..., xn ) : Ax b, x 0
называется множеством допустимых планов задачи
(14) или допустимым множеством.
25.
Опр.2 Множество векторов D x ( x1 , x2 ,..., xn ) : Ax b, x 0называется
множеством
допустимых
планов
задачи (15) или допустимым множеством.
Опр.3 Вектор x * ( x1* , x2* ,..., xn* ) D (из множества допустимых
планов) называется оптимальным планом задачи
(14), или задачи (15), если для любого вектора x из
допустимого множества
выполняется неравенство
C(x) C (x*).
Опр.4 Пусть x D – допустимый план ЗЛП (14) или (15).
Носителем плана x называется множество индексов
x i : xi 0, где i 1, n .
26.
Замечание. Неотрицательные переменные в допустимомплане могут быть расположены в произвольном
порядке.
Опр.5 Число положительных компонент плана x будем
называть мощностью носителя плана и обозначать
х или .
Опр.6 Если векторы Аik , где k 1, m, а m – число
уравнений ЗЛП (15), являются линейно
независимыми векторами, то будем говорить, что
данные векторы образуют базис ЗЛП.
27.
Обозначим множество индексов i1 , i2 ,..., im через ,тогда базис будем обозначать таким образом
Ak k
или просто А .
Векторы Ak называются базисными векторами, а сама
матрица А называется базисной матрицей.
Опр.7 Рассмотрим векторы Ai Rm , i 1, k , где k некоторое
целое число. Если равенство 1 A1 2 A2 ... k Ak 0
возможно только в том случае, когда числа
1 2 ... k 0 , то векторы A1, A2, …, Ak
называются линейно независимыми. Векторы
A1,
A2, …, Ak могут быть линейно независимыми
только, если k m.
28.
C ( x) (c, x) maxA1 x1 A2 x2 ... An xn b
x , x ,..., x 0
n
1 2
a1 j
a2 j
Aj
,
......
a
mj
,
(16)
j 1, n
Опр.8 Пусть x D – допустимый план ЗЛП (16) и – его
носитель. Если векторы Ai , i , линейно
независимые, то план x называется базисным
допустимым планом (БДП) или базисным
допустимым решением (БДР).
29.
Базисный план называется невырожденным, еслиБазисный план называется вырожденным, если
П р и м е р.
С ( x ) 5 x1 7 x 2 max
3 x1 5 x 2 18
5 x1 4 x 2 2
x ,x 0
1 2
Приведем ее к канонической форме записи:
С ( x) 5 x1 7 x 2 max
3 x1 5 x 2 x3 18
5 x1 4 x 2 x 4 2
x ,x ,x ,x 0
1 2 3 4
=m.
< m.
30.
В данной задаче имеются следующие векторы:5
3 ;
1 ;
0 .
;
A1 A2 A3 A4
4
5
0
1
A3, A4 – единичные векторы, которые являются линейно
независимыми, следовательно, они образуют базис ЗЛП.
Вектор x = (0, 0, 18, 2) – это БДП.




























 programming
programming








