ЛР2 (2)

1.

Лабораторная работа 2.
Линейная регрессия. Криволинейная
регрессия
В СДО:
задания для лабораторной работы;
пример и указания по выполнению в Excel
(ознакомиться!)
Цель: по выборке наблюдений над парой СВ:
- проверить, можно ли считать зависимость между наблюдаемыми
величинами линейной;
- получить линейное уравнение зависимости между этими
величинами, используя метод наименьших квадратов (МНК);
- подобрать наилучшую аппроксимирующую функцию с помощью
диаграмм Excel;
- получить уравнение наилучшей аппроксимирующей функции,
сведя ее к линейной зависимости и использовав МНК.

2.

t
U
0
95
1
75
2
55
3
40
4
30
5
20
6
15
7
10
8
10
9
5
10
5
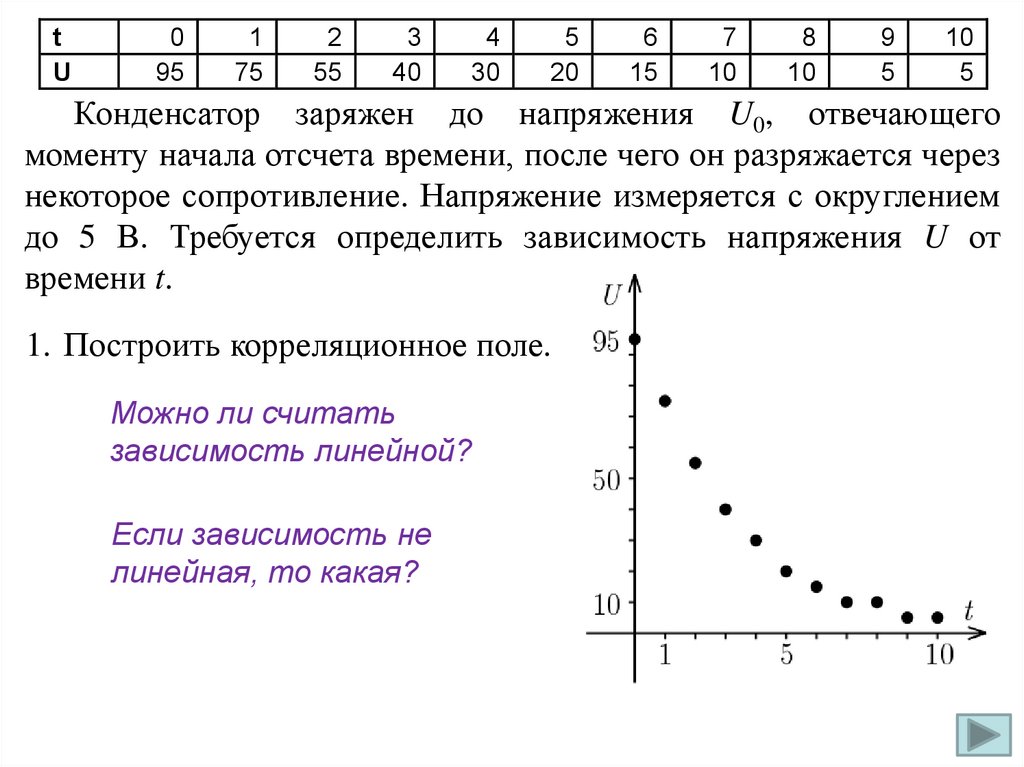
Конденсатор заряжен до напряжения U0, отвечающего
моменту начала отсчета времени, после чего он разряжается через
некоторое сопротивление. Напряжение измеряется с округлением
до 5 В. Требуется определить зависимость напряжения U от
времени t.
1. Построить корреляционное поле.
Можно ли считать
зависимость линейной?
Если зависимость не
линейная, то какая?

3.

t
U
0
95
1
75
2
55
3
40
4
30
5
20
6
15
7
10
8
10
9
5
10
5
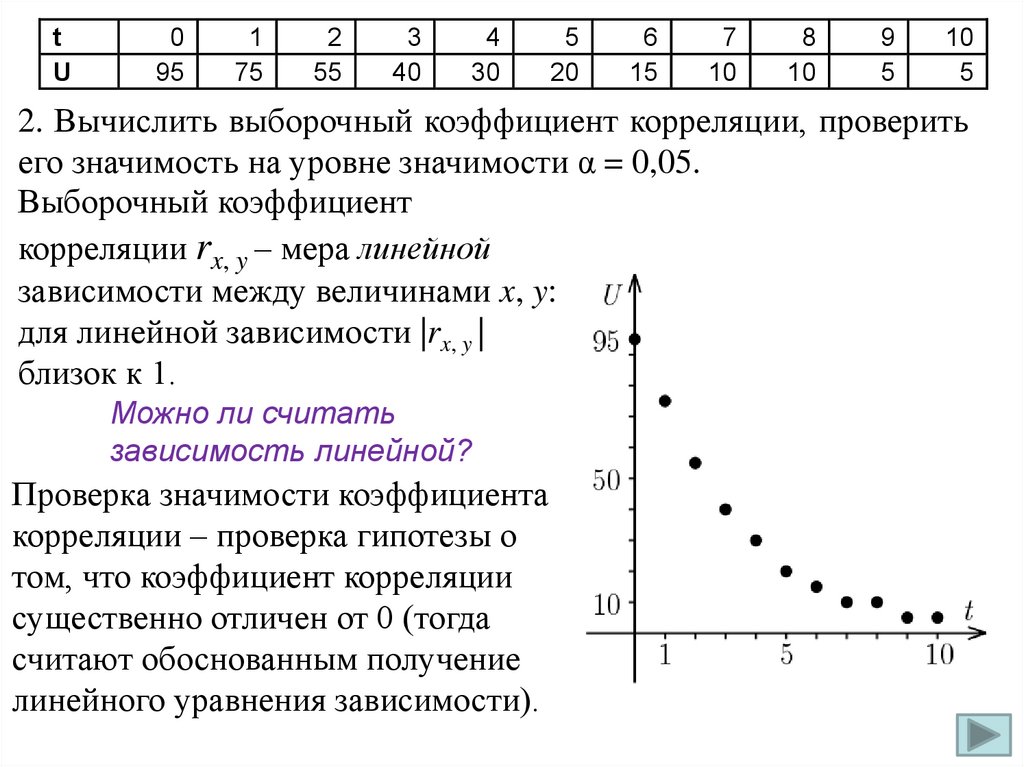
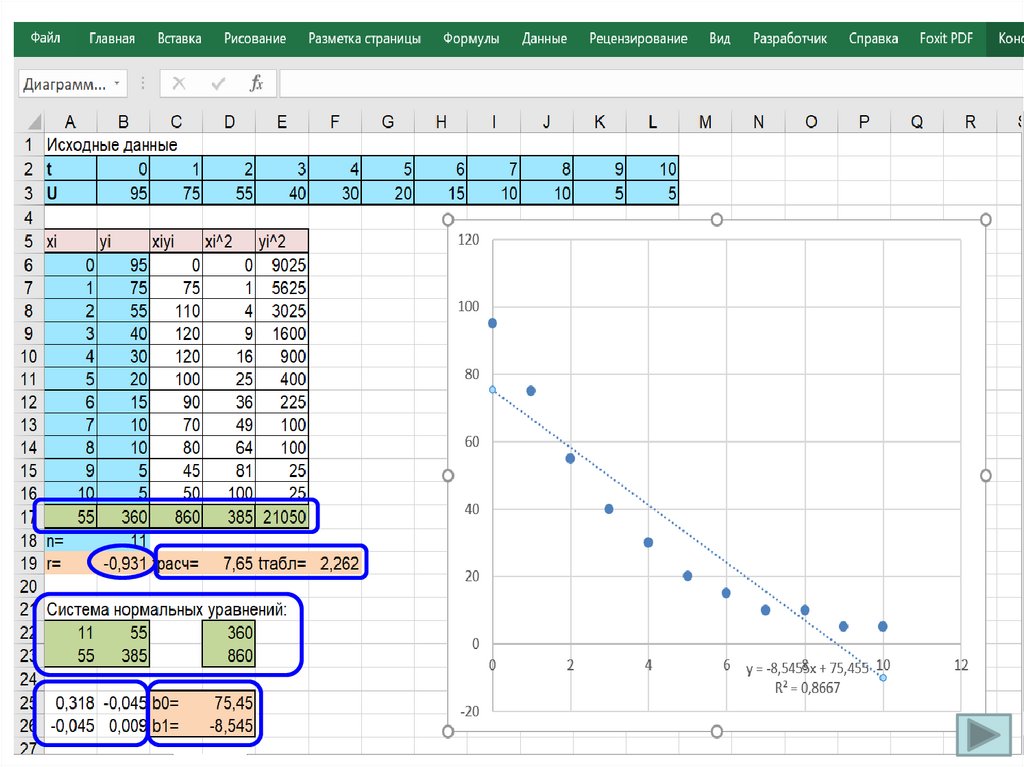
2. Вычислить выборочный коэффициент корреляции, проверить
его значимость на уровне значимости α = 0,05.
Выборочный коэффициент
корреляции rx, y – мера линейной
зависимости между величинами x, y:
для линейной зависимости |rx, y |
близок к 1.
Можно ли считать
зависимость линейной?
Проверка значимости коэффициента
корреляции – проверка гипотезы о
том, что коэффициент корреляции
существенно отличен от 0 (тогда
считают обоснованным получение
линейного уравнения зависимости).

4.

t
U
0
95
1
75
2
55
3
40
4
30
5
20
6
15
7
10
8
10
9
5
10
5
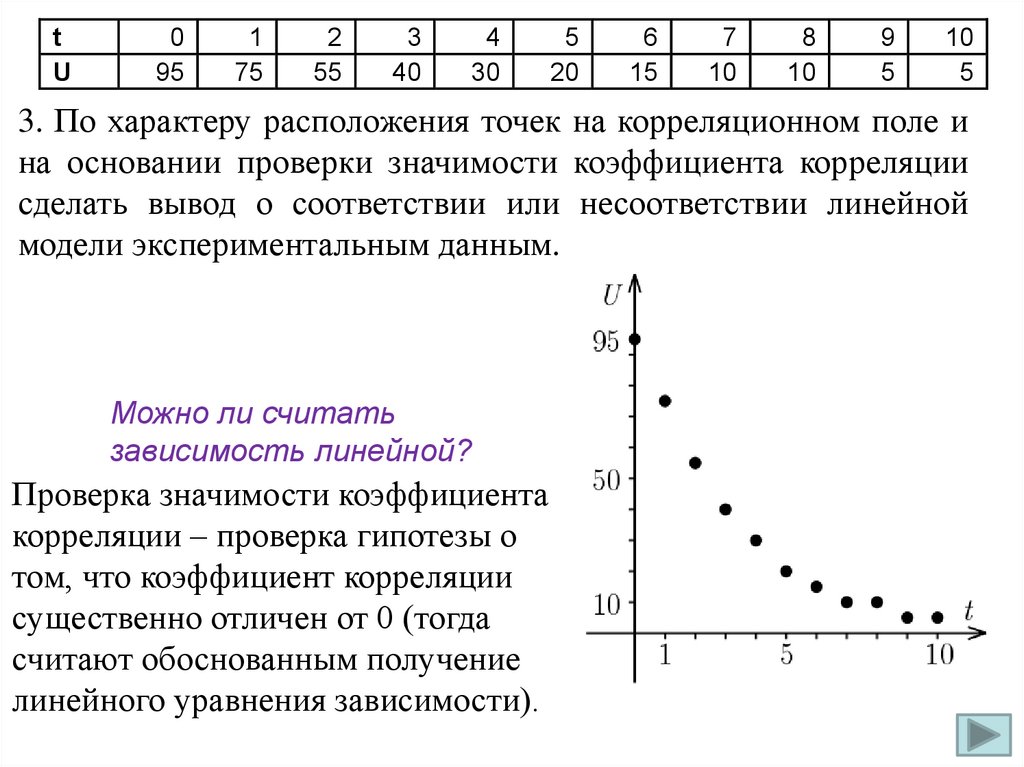
3. По характеру расположения точек на корреляционном поле и
на основании проверки значимости коэффициента корреляции
сделать вывод о соответствии или несоответствии линейной
модели экспериментальным данным.
Можно ли считать
зависимость линейной?
Проверка значимости коэффициента
корреляции – проверка гипотезы о
том, что коэффициент корреляции
существенно отличен от 0 (тогда
считают обоснованным получение
линейного уравнения зависимости).

5.

xt
U
y
0
95
1
75
2
55
3
40
4
30
5
20
6
15
7
10
8
10
9
5
10
5
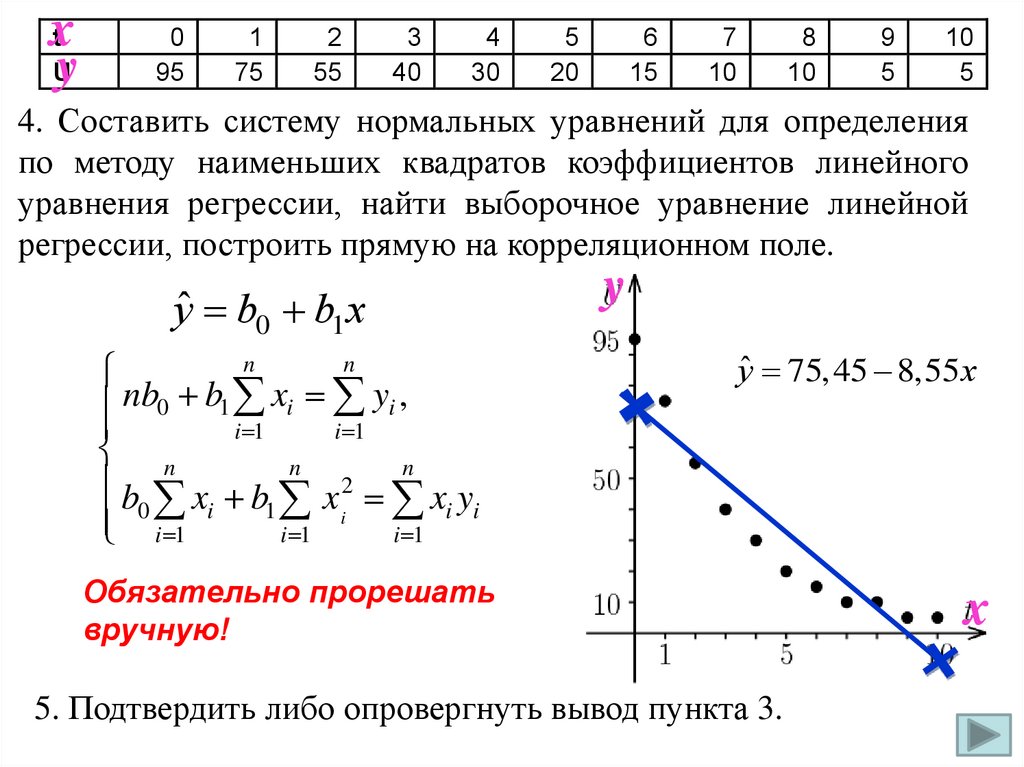
4. Составить систему нормальных уравнений для определения
по методу наименьших квадратов коэффициентов линейного
уравнения регрессии, найти выборочное уравнение линейной
регрессии, построить прямую на корреляционном поле.
у̂ b0 b1x
n
n
nb0 b1 xi yi ,
i 1
i 1
n
n
n
2
b x b x x y
0 i 1 i 1 i 1 i i 1 i i
y
уˆ 75,45 8,55 x
Обязательно прорешать
вручную!
5. Подтвердить либо опровергнуть вывод пункта 3.
x

6.

7.

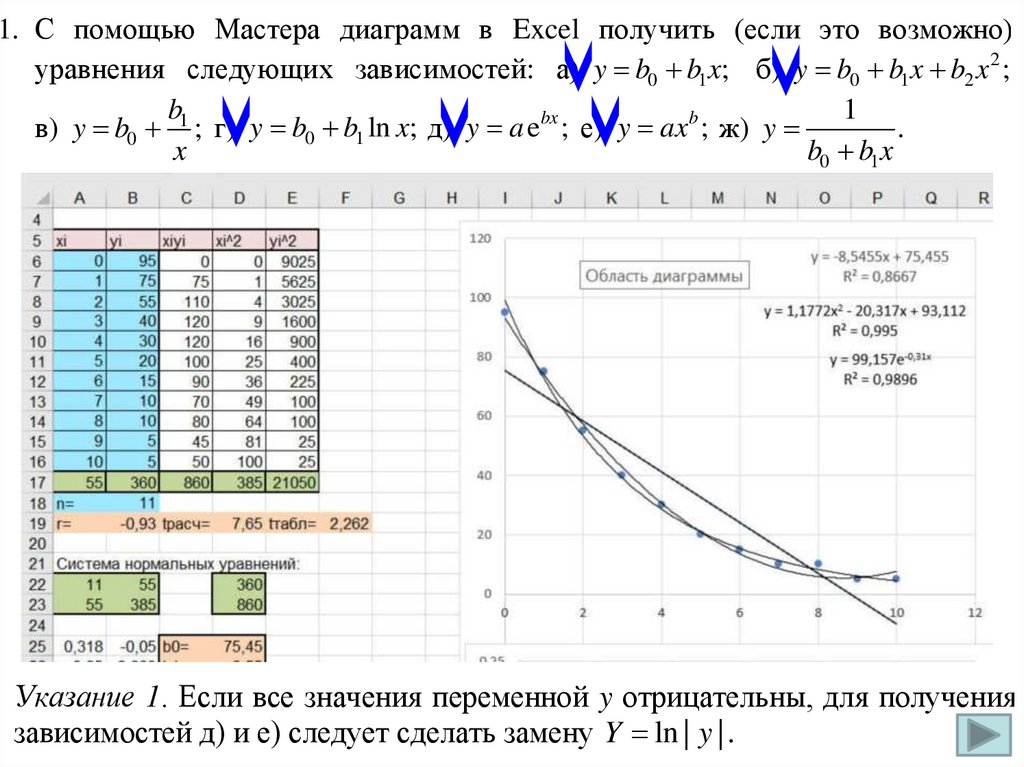
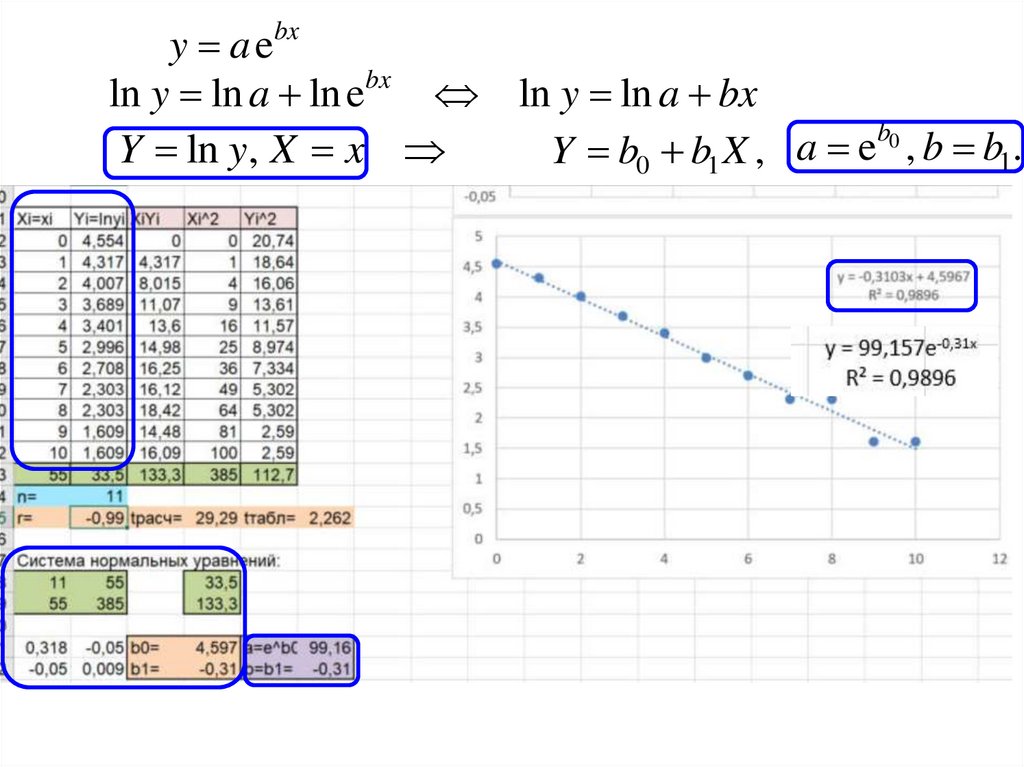
1. С помощью Мастера диаграмм в Excel получить (если это возможно)
уравнения следующих зависимостей: а) y b0 b1x; б) y b0 b1x b2 x 2 ;
1
b
в) y b0 1 ; г) y b0 b1 ln x; д) y a ebx ; е) y ax b ; ж) y
.
x
b0 b1x
Указание 1. Если все значения переменной y отрицательны, для получения
зависимостей д) и е) следует сделать замену Y ln | y | .

8.

1. С помощью Мастера диаграмм в Excel получить (если это возможно)
уравнения следующих зависимостей: а) y b0 b1x; б) y b0 b1x b2 x 2 ;
1
b
в) y b0 1 ; г) y b0 b1 ln x; д) y a ebx ; е) y ax b ; ж) y
.
x
b0 b1x
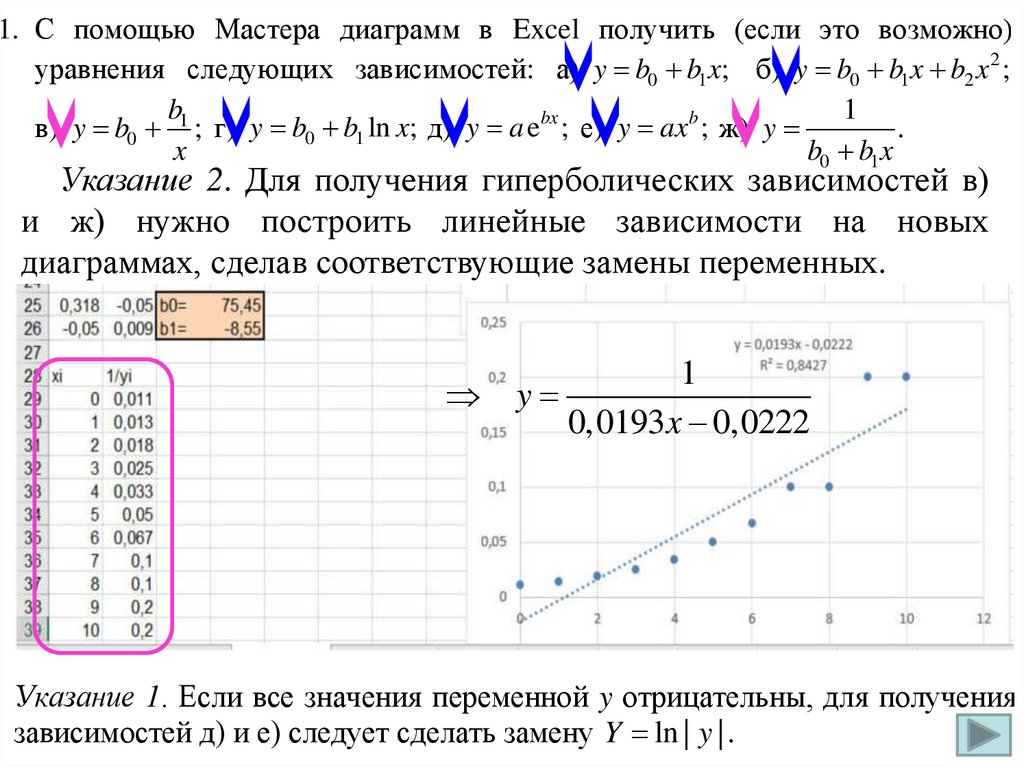
Указание 2. Для получения гиперболических зависимостей в)
и ж) нужно построить линейные зависимости на новых
диаграммах, сделав соответствующие замены переменных.
1
y
0,0193x 0,0222
Указание 1. Если все значения переменной y отрицательны, для получения
зависимостей д) и е) следует сделать замену Y ln | y | .

9.

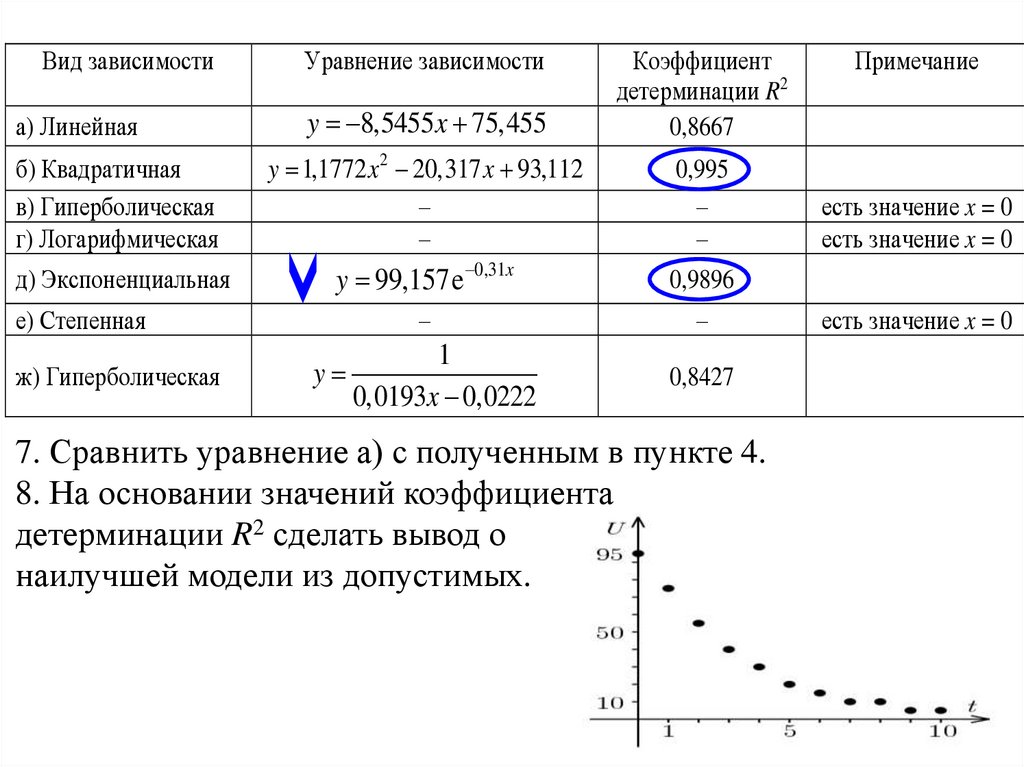
Вид зависимости
y 8,5455x 75,455
Коэффициент
детерминации R2
0,8667
б) Квадратичная
в) Гиперболическая
г) Логарифмическая
y 1,1772 x 2 20,317 x 93,112
–
–
0,995
–
–
д) Экспоненциальная
y 99,157e 0,31x
0,9896
–
–
а) Линейная
Уравнение зависимости
е) Степенная
ж) Гиперболическая
y
1
0,0193x 0,0222
0,8427
7. Сравнить уравнение а) с полученным в пункте 4.
8. На основании значений коэффициента
детерминации R2 сделать вывод о
наилучшей модели из допустимых.
Примечание
есть значение x = 0
есть значение x = 0
есть значение x = 0

10.

9. В случае б): составить систему нормальных уравнений для
определения по методу наименьших квадратов коэффициентов
квадратичного уравнения регрессии; найти выборочное
квадратичное уравнение регрессии.
В случаях в)-ж): указать замену переменных, позволяющую
свести выбранную зависимость к линейной; построить
корреляционное поле в новых переменных; составить систему
нормальных уравнений для определения по методу наименьших
квадратов коэффициентов линейного уравнения регрессии в
новых переменных; найти выборочное уравнение линейной
регрессии, построить прямую на корреляционном поле; сделав
обратную замену, получить уравнение регрессии в натуральных
переменных.

11.

y a ebx
ln y ln a ln ebx ln y ln a bx
b0
Y ln y, X x
Y b0 b1 X , a e , b b1.